网络编码实现了网络传输信息再编码功能, 能有效提升网络的传输容量和健壮性, 在未来通信网络的研究和设计中具有重要的应用价值[1-5]。当前, 安全问题仍是阻碍网络编码推广应用的一个技术瓶颈[6]。其中, 如何保证数据传输的机密性是安全研究领域的重要课题。
Cai等[7]系统描述了防搭线窃听网络编码的设计原理和基本模型。假设攻击者窃听网络信道的边数受限, 则该模型可以在信息理论意义上被证明是最优的[8]。Feldman等[9]证明了安全网络码的构造可以规约为具有某种广义距离特征的线性码的构造问题。由此, Rouayheb等[10]给出了一种具体的方案设计实例。Bhattad和Narayanan对文献[7]进行推广, 提出了一种“弱安全”的安全概念, 可使信源在不引入随机冗余的情况下仍能使网络传输达到网络最大通信容量[11]。文献[12-13]则结合最大秩距离码构造了一类通用的网络编码防窃听模型。
上述方案假定窃听者的窃听能力有限,且方案的构造严格依赖于网络拓扑和充分大的编码域。文献[14-15]利用伪随机函数减少了该类方案由于引入随机性而带来的带宽开销, 但该方案却要随机化所有的明文数据, 在执行效率上仍不理想。
为此, 研究者将传统密码手段和网络编码路由编码策略相结合来实现消息的机密性保护。Lima等[16]研究了随机网络编码固有的代数安全属性。Vilela等[17]将信源消息的保护转化为对其预编码矩阵的加密隐藏。进一步地, 文献[18]通过局部加密实现了整个文件的机密性。与文献[17, 20]类似, 该方案通信开销仍然过大。虽然文献[19]利用了同态性编码实现了消息的线性混淆, 能有效抵御攻击者对网络流量的特征分析, 但此方法却带来了较大的编码计算和通信开销。Zhang等[21]提出了P-Coding, 使用置换加密技术实现信源编码的保密性, 但需要加密所有的信源数据。在攻击者窃听网络任意信道子集的条件下,Cheng等[22]研究了P2P网络中非完美及完善安全网络编码的理论构造。但是,该方案构造过于复杂, 无法很好地适用于无线安全网络的传输。最近, 文献[23]利用最大距离可分码的性质构造了一种具有可度量属性的安全方案。但是, 该方案的编码开销仍较大, 有待进一步改进。
综上所述, 基于信息理论的完善保密性的实现条件过于苛刻, 很难在一般的网络条件下实现如此高的安全强度。现有基于密码学的方案大都需要隐藏或保护编码信息, 其安全实现的计算复杂度和通信负载都较高。这些问题存在的原因在于它们并没有将经典密码学中的实用技术与网络编码的组合特性进行合理有效的融合[24]。
1 网络和敌手模型假设当前网络中信源节点可以利用网络编码传输模式和信宿节点进行保密通信。在通信过程之初, 信源把待传输消息编码成一个连续的代(即generation,或会话)消息序列。各代消息均由m个向量vi=(vi1, vi2, …, vin)∈Fqn组成,i=1, 2, …, m。显然, 各代消息都可以看成是一个维数为m×n的矩阵V=(v1T, v2T, …, vmT)T。
不失一般性, 假定信源是可信的, 窃听者只能执行概率多项式时间的分析算法。该窃听者可以收集到网络信道中传输的所有消息(但无法知道密钥信息), 也知晓网络中所有节点的编码或译码方法, 并企图由此提取对自己有用的机密破解信息。
2 基本方案本节仅描述适用于随机网络编码的安全方案。为简单起见, 下文中只说明网络编码系统中一次会话(标记为id)的过程。
在网络配置阶段, 系统需要分别引入一个伪随机置换(PRP)f1:I×Fq→Fq和一个伪随机函数(PRF) f2:I×K×[m]×[m]→Fq, 其中I和K分别表示会话标识符的取值域和密钥集合。
2.1 信源编码步骤1 信源借助于f1把会话id中的消息向量v1随机化为向量u1∈Fqn, 即有

|
这里,
1) 当i=1时,
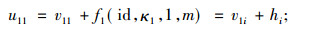
|
2) 当i=2, 3, …, n时,
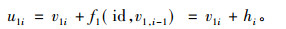
|
步骤2 信源利用f2生成维数为m×m的矩阵A=(a)ij,
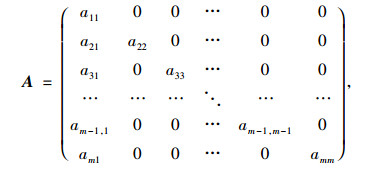
|
这里有
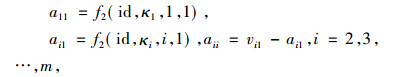
|
其中{κ1, κ2, …, κm}⊂K且vi1≠ai1, aii≠0。
步骤3 信源计算
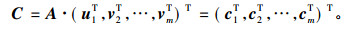
|
(1) |
步骤4 信源发送消息向量c1, c2, …, cm。
2.2 信宿解码当信宿接收到属于会话id的数据包后, 构造全局译码矩阵, 利用高斯消元法恢复出信源消息向量c1, c2, …, cm, 最后执行2.1节中步骤的逆操作。
3 安全性分析为分析方便, 这里假设信源消息符号在有限域Fq上服从均匀独立分布。
定理1 已知密文向量c1, c2, …, cm, 窃听者无法恢复该密文对应的明文向量v1, v2, …, vm。
证 明 既然vi1已经被加密保护, 所以该窃听者无法得到vi1的任何信息。
由于窃听者可以正确解出当前信源发送的消息向量c1, c2, …, cm。“聪明”的窃听者可以利用式(1)的构造方法生成如下线性方程组,去解明文向量矩阵V中的任意一列(比如, 第j列)的明文vj=(v1j, v2j, …, vmj),
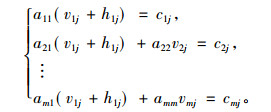
|
(2) |
其中,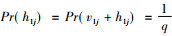
综上可得, 窃听者能正确猜测明文任意列的最大概率仅为
由定理1可知, 方案的安全性最终将取决于矩阵A和所有自由变量h1j的随机性。
定理2 对于仅能执行概率多项式时间算法的窃听者来说, 推导编码矩阵A的难度不会弱于猜测明文的难度[24]。
根据定理2, 当窃听者无法得到所有h1j的信息时, 编码矩阵A是足够安全的。这说明矩阵A在保密通信中是可以连续重复地多代使用。
4 性能分析 4.1 安全开销本方案有效地利用了传统密码学中的随机化工具, 实现了与文献[17-18, 23]中方案对等的安全性。在每次会话中都能有效地引入随机编码信息, 从而保证了连续各次会话消息的保密性。
方案在执行过程中涉及到的主要计算来源于随机函数的操作。在实际应用中, PRP和PRF都可用分组密码的构造模式来快速实现, 这部分开销是可以忽略的。由此, 本方案中需要完成的消息随机化规模成为影响算法效率的主要因素。本方案的消息随机化比率为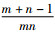
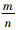
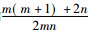
值得关注的是, 与文献[7-8, 22]相比, 本文方案无需对窃听者的窃听信道数目进行任何的限制, 实现了在应用中更容易操作的安全性。
4.2 通信开销本方案无需为信源编码引入额外的编码冗余信息, 故网络信息传输能力可以达到网络的最大容量。文献[17-18]中的方案在运行时,收发端需要实时传递预编码信息, 这消耗了至少为m的带宽资源。此外, 文献[14-15, 19-21]中的方案的安全性依赖于充分大的编码域, 与本方案的通信传输效率相比相差甚远。
4.3 方案比较表 1给出了部分代表性方案在信源安全编码时的性能参数。可以看出, 该方案在编码计算和通信开销方面具有较为明显的性能优势。该方案将现有方案的编码复杂度从O(m2n)减少为O(mn)。这在网络安全传输中具有重要的现实意义。
|
|
表 1 代表性方案性能参数比较 Tab. 1 Comparison of performance parameters for representative schemes |
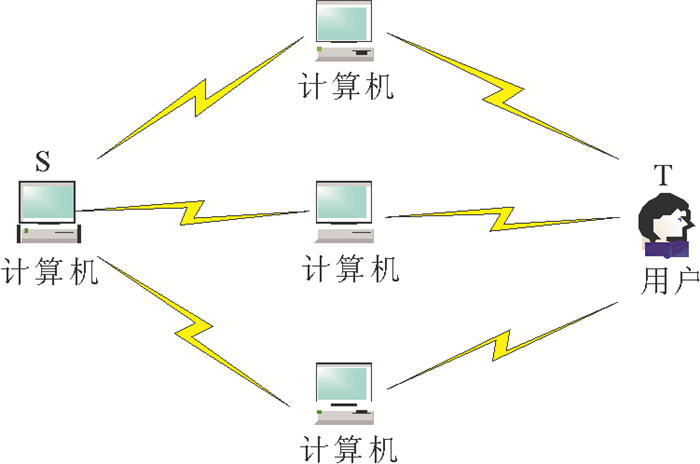
为了验证本文方案在网络传输中的相对性能,在奔腾Core2-2.80 GHz处理器上利用Matlab R2010a对单源两跳网络(即信源S通过三个中继节点向一个接收用户T发送数据, 如图 1所示)中对本文方案、文献[17]和[23]中的方案(分别记作S0, S1, S2)进行模拟对比实验。网络仅利用UDP协议以均匀速率传输数据, 数据的加解密操作采用AES算法。编码参数m=20, n=1 024 bytes, q=216。这里, 假定各条链路容量均相同, 实验中没有考虑链路传输时延及密钥分发过程。
|
图 1 单源两跳网络 Fig. 1 Single-source two-hop network |
首先考虑各方案在信源端的编码计算效率方面的相对性能。安全算法的性能指标采用了信源单位时间内完成的代编码数目来衡量。该指标值的大小取决于代编码过程中的加密量和乘法计算量。由于各代编码相对独立, 故每个方案中各代编码时间相同。因此, 信源编码处理时间必然与代消息规模成正比例增长。
在对单代消息进行源编码过程中, 方案S0主要操作是随机函数和乘法计算。随机函数运算速度较快, 一般可以忽略。方案S0的乘法计算量远小于方案S1和S2。方案S2仅涉及线性组合和加密操作。由表 1可知, 方案S0的源编码(主要是乘法操作)复杂度明显低于方案S1。此外, 方案S1和S2对每代消息的加密量都较少, 后者的加密量略高于前者, 但由于都可以采用了流密码处理, 故在加密复杂度方面相差甚微。
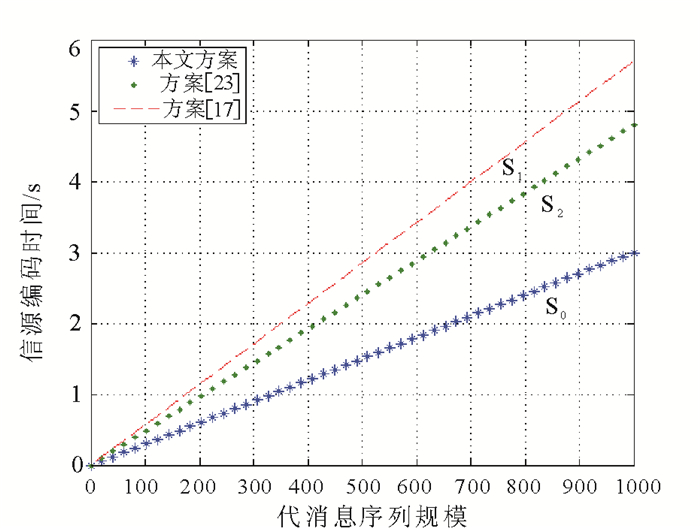
图 2给出了在连续代消息序列规模数量逐渐增大的情况下, 上述3种方案源编码需要的时间t的拟合结果。本文方案的源编码速率近似为方案S1的1.9倍, 方案S2的1.6倍。进一步可知, 当发送数据量为1Gbit时, 方案S0,S1和S2源编码所需要的计算时间分别为79s,126s和149s。相比之下, 本文方案具有更好的编码性能。
|
图 2 3种典型方案信源编码时间性能比较 Fig. 2 Comparison of source coding time performance of three typical schemes |
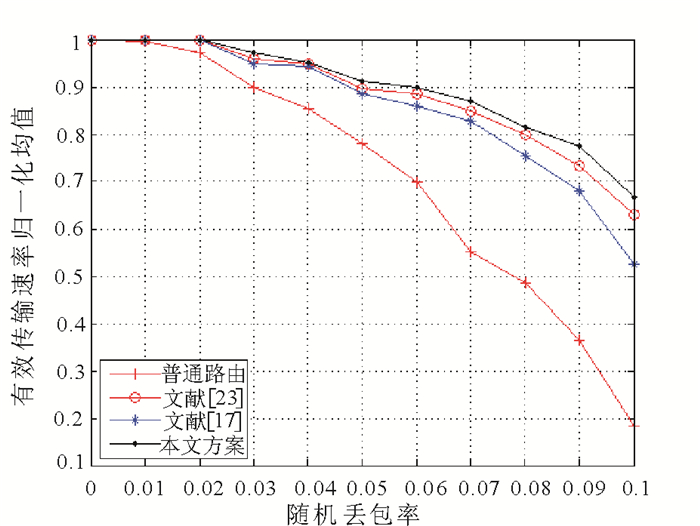
其次, 考虑到网络编码在不可靠网络中的性能优势和实际通信链路的不稳定性(链路中存在随机丢包), 下面对方案S0, S1, S2和普通加密路由传输方案对实际通信系统中的性能影响做进一步测试。这里假定每条链路中的随机丢包率均为p。实验采用有效传输速率的归一化均值r来衡量各方案传输效率。
图 3说明信源编码性能对不可靠网络系统的传输效率产生了较为明显的影响。实验中没有考虑冗余包的发送, 方案S0, S1, S2的传输性能都比普通加密路由传输方案要好。但是, 这3种方案的传输效率也没有呈现前文图 2中的线性相对关系。实际上, 方案S1, S2的传输速率相对较慢, 其主要原因在于这类方案的安全编码计算复杂度都较大, 编码效率较差, 致使其对网络通信资源的利用率也较低, 再加上方案S1在通信中需要更多的带宽资源, 最终导致方案S1, S2的系统传输性能比方案S0较为逊色。实验结果不仅验证了网络编码在信道有随机丢包的情况下相对于普通路由传输的健壮性能, 而且也论证了本文方案在实际场景下的系统性能方面的相对优势。
|
图 3 本文方案和典型安全方案的通信性能比较 Fig. 3 Communication performance comparison between the proposed scheme and the typical security schemes |
本文主要利用随机化线性编码策略, 给出了一种可以有效适用于网络编码通信系统的高效防窃听攻击的安全方案。通过理论探索和实验测试, 进一步论证了网络编码的信息组合特性为安全方案的设计和实现带来的性能优势。这种基于代数意义下的安全设计策略, 可以有效地减少安全实现的计算复杂度和通信负载。
文中假设网络节点之间都是相互信任和协作的关系, 无法实现网络编码路由中存在恶意节点的安全需求。在特定应用中引入可信度安全控制模型, 可以有效地节省节点的能量和空间开销[25]。因此, 下一步深入的研究工作是将可信计算技术融入到网络编码传输体制中, 开发一些更符合具体应用场景的安全网络编码方案。
| [1] |
AHLSWEDE R, CAI N, LI S Y R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216. DOI:10.1109/18.850663 |
| [2] |
LI S Y R, YEUNG R W, CAI N. Linear network coding[J]. IEEE Transactions on Information Theory, 2003, 49(2): 371-381. DOI:10.1109/TIT.2002.807285 |
| [3] |
BASSOLI R, MARQUES H, RODRIGUEZ J, et al. Network coding theory: A survey[J]. IEEE Communications Surveys & Tutorials, 2013, 15(4): 1950-1978. |
| [4] |
MATSUDA T, NOGUCHI T, TAKINE T, et al. Survey of network coding and its applications[J]. IEICE Transactions on Communications, 2011, 94(3): 698-717. |
| [5] |
YAO H, SILVA D, JAGGI S, et al. Network codes resilient to jamming and eavesdropping[J]. IEEE/ACM Transactions on Networking (TON), 2014, 22(6): 1978-1987. DOI:10.1109/TNET.2013.2294254 |
| [6] |
TALOOKI V N, BASSOLI R, LUCANI D E, et al. Security concerns and countermeasures in network coding based communication systems: A survey[J]. Computer Networks, 2015, 83: 422-445. DOI:10.1016/j.comnet.2015.03.010 |
| [7] |
CAI N, CHAN T. Theory of secure network coding[J]. Proceedings of the IEEE, 2011, 99(3): 421-437. DOI:10.1109/JPROC.2010.2094592 |
| [8] |
CAI N, YEUNG R W. Secure network coding on a wiretap network[J]. IEEE Transactions on Information Theory, 2011, 57(1): 424-435. DOI:10.1109/TIT.2010.2090197 |
| [9] |
FELDMAN J, MALKIN T, STEIN C, et al. On the Capacity of Secure Network Coding[EB/OL]. [2015-07-01]. http://www.cs.columbia.edu/~rocco/Public/sflow_allerton_final.pdf.
|
| [10] |
ROUAYHEB S Y E, SOLJANIN E, SPRINTSON A. Secure network coding for wiretap networks of type Ⅱ[J]. IEEE Transactions on Information Theory, 2012, 58(3): 1361-1371. DOI:10.1109/TIT.2011.2173631 |
| [11] |
BHATTAD K, NARAYANAN K R. Weakly secure network coding[EB/OL]. [2015-07-01]. http://www.tamu.edu/faculty/commtheory/papers/weaklysecure_netcod05.pdf.
|
| [12] |
SILVA D, KSCHISCHANG F R. Universal secure network coding via rank-metric codes[J]. IEEE Transactions on Information Theory, 2011, 57(2): 1124-1135. DOI:10.1109/TIT.2010.2090212 |
| [13] |
SILVA D, KSCHISCHANG F R. Universal secure error-correcting schemes for network coding[C]//IEEE International Symposium on Information Theory Proceedings.IEEE, 2010: 2428-2432.
|
| [14] |
ADELI M, LIU H. Secure network coding with minimum overhead based on hash functions[J]. IEEE Communications Letters, 2009, 13(12): 956-958. DOI:10.1109/LCOMM.2009.12.091648 |
| [15] |
WEI Y W, ZHEN Y, GUAN Y. Efficient weakly-secure network coding schemes against wiretapping attacks[C]//Proceedings of the IEEE International Symposium on Network Coding (NetCod), Toronto: IEEE Press, 2010: 1-6.
|
| [16] |
LIMA L, MEDARD M, BARROS J. Random linear network coding: A free cipher?[C]//Proceedings of IEEE International Symposium on Information Theory, Nice: IEEE Press, 2007: 546-550.
|
| [17] |
VILELA J P, LIMA L, BARROS J. Lightweight security for network coding[C]//Proceedings of the IEEE International Conference on Communications (ICC). Beijing: IEEE Press, 2008: 1750-1754.
|
| [18] |
LIMA L, GHEORGHIU S, BARROS J, et al. Secure network coding for multi-resolution wireless video streaming[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(3): 377-388. DOI:10.1109/JSAC.2010.100409 |
| [19] |
FAN Y F, JIANG Y X, ZHU H J, et al. Network coding based privacy preservation against traffic analysis in multi-hop wireless networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(3): 834-843. DOI:10.1109/TWC.2011.122010.100087 |
| [20] |
GUO Q, LUO M X, LI L X, et al. Secure network coding against wiretapping and Byzantine attacks[J]. EURASIP Journal on Wireless Communications and Networking, 2009(1): 1-9. |
| [21] |
ZHANG P, JIANG Y X, LIN C, et al. P-Coding: Secure network coding against eavesdropping attacks[C]//Proceedings of IEEE INFOCOM, San Diego: IEEE Press, 2010: 1-9.
|
| [22] |
CHENG F, YEUNG R W. Performance bounds on a wiretap network with arbitrary wiretap sets[J]. IEEE Transactions on Information Theory, 2014, 60(6): 3345-3358. DOI:10.1109/TIT.2014.2315821 |
| [23] |
LIU G J. Practical schemes for tunable secure network coding[J]. KSⅡ Transactions on Internet and Information Systems, 2015, 9(3): 1193-1209. |
| [24] |
刘光军.安全网络编码及其应用[D].西安: 西安电子科技大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10701-1013297766.htm
|
| [25] |
冉崇善, 车育. 基于快速移动节点的Ad hoc网络可信度模型及可信路由协议[J]. 西北大学学报(自然科学版), 2015, 45(2): 213-217. |
 2017, Vol. 47
2017, Vol. 47
