为了重建格理论, 实现哲学中概念与概念层次结构的数学化描述, 德国数学家Wille R.于1982年提出了形式概念分析理论(Formal Concept Analysis, FCA) [1-2]。FCA通过内涵和外延的依赖关系及概念的层次关系直观简洁的反映隐藏在数据集中的信息, 所以近年来它在中医药成分分析[3], 专家系统[4], 数据挖掘[5]以及软件工程[6-7]等领域得到了广泛的应用。
与其他理论相结合进行研究也是FCA的一个重要的研究方向。由此产生了一系列新的概念格模型[8-19]。例如, Düntsch和Gediga在文献[8]中把粗糙集中的上下近似引入形式概念分析, 提出了面向属性概念格。类似地, Yao[9]给出了面向对象概念格的定义。随后, Ma等[10]研究了面向对象概念格的构造方法。结合三支决策, Qi等[11-12]提出了三支概念格。随后, Qian等[13]利用背景的运算研究了三支概念格的构造方法。刘琳等[14]基于三支概念格研究了决策形式背景上的规则提取理论。
区间集概念格[15]是将区间集理论[16]与概念格理论相结合而产生的一种新的概念格模型。其本质思想是把概念中表示外延与内涵的集合推广到区间集, 利用区间集所反映的不确定信息把经典概念扩展到区间集概念。区间集概念格继承并推广了概念格的方法和技巧, 是研究概念动态变化的有效工具。后来, 在不完备背景上, Yao在文献[17]中将区间集理论与三支概念分析结合, 提出了区间集算子并对文献[18]中的概念格给出了相应的区间集表示。
区间集概念格被提出之后, 关于区间集概念的计算目前只有利用定义计算的方法, 即先求出对象集(属性集)的所有区间集, 再利用区间集算子判断是否可以生成区间集概念。据计算, 若对象(属性)集所含元素的个数是n(m), 那么所需要遍历的所有区间集的个数为3n(3m)。而用形式概念的定义计算所有经典概念, 只需遍历的所有子集的个数为2n(2m), 因此, 利用定义计算区间集概念的方法计算量十分大。然而, 区间集概念格的其他方面研究又离不开区间集概念格的建造。因此, 寻找新的方法构造区间集概念格势在必行。
本文在回顾形式概念分析、区间集以及区间集概念格相关理论的基础之上, 研究了区间集概念格与经典概念格的联系, 进而提出了一种基于经典概念格构造区间集概念格的方法, 并在此基础上给出了相应的算法, 分析了其时间复杂度。
1 相关概念及基本理论 1.1 形式概念分析形式概念分析的研究基础是刻画对象与属性之间的二元关系的数据集——形式背景, 而以此为基础获取的格结构模型是该理论的核心数据结构——概念格, 其能生动简洁地体现概念之间的泛化和特化关系[1-2]。
定义1 [1]设(G, M, I)为一个形式背景, 其中G={g1, …, gp}为对象集, 每个gi(i ≤ p)称为一个对象; M={m1, …, mq}为属性集, 每个mj(j ≤ q)称为一个属性; I为G和M之间的二元关系, I⊆G×M。若(g, m) ∈I, 则表示对象g有属性m, 也记为gIm。
当G与M均为有限集合时, 形式背景(G, M, I)可以用一个有限二维表来表示。
在对象子集X⊆G和属性子集A⊆M上定义一对对偶算子如下:
X*={m|m∈M, ∀g∈X, gIm},
A*={g|g∈G, ∀m∈A, gIm}。
X*表示X中所有对象共同具有的属性集合, A*表示共同具有A中所有属性的对象集合。如果一个二元组(X, A)满足X*=A, 且A*=X, 则称(X, A)是一个形式概念, 简称概念。其中, X称为概念的外延, A称为概念的内涵。
用L(G, M, I)表示形式背景(G, M, I)的全体概念, 在偏序关系(X1, A1)≤(X2, A2)⇔X1⊆X2(⇔A1⊇A2)下, 可以证明
(X1, A1)∧(X2, A2)=(X1∩X2, (A1∪A2)**),(X1, A1)∨(X2, A2)=((X1∪X2)**, A1∩A2),也是概念, 从而L(G, M, I)是格, 并且是完备格, 称其为形式背景(G, M, I)的概念格(文中称为经典概念格)。若对于任意的g⊆G和m⊆M, 都有g*≠∅, g*≠M, m*≠G及m*≠∅, 则称形式背景(G, M, I)为正则的形式背景。
例1 表 1是形式背景(G, M, I), 其中G={1, 2, 3, 4}, M={a, b, c, d, e}, 显然其为正则的非净化的形式背景。其概念格如图 1所示。
|
|
表 1 形式背景(G, M, I) Tab. 1 A formal context (G, M, I) |
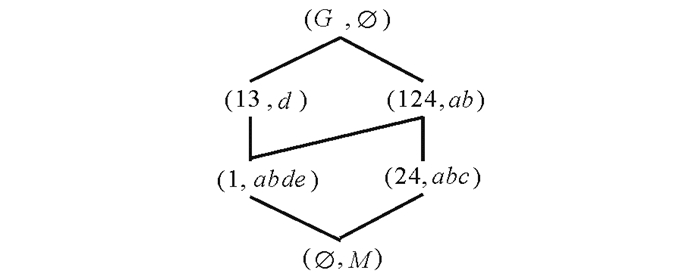
|
图 1 L(G, M, I) Fig. 1 L(G, M, I) |
由于信息的不完备性, 很难精确地用一个子集来描述论域上概念的外延。而区间集利用粗糙集下、上近似的思想, 通过一个下界和上界对论域的子集进行描述, 由此可给出该集合的真实外延。下面我们首先回顾区间集的基本概念[16]。
定义2[16] 设U是有限论域, P(U)为U的幂集。定义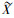
注 ①区间集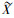
类似于经典集合之间的运算, Yao给出了区间集间的运算[16]。
定义3[16] 设U是有限论域, 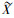
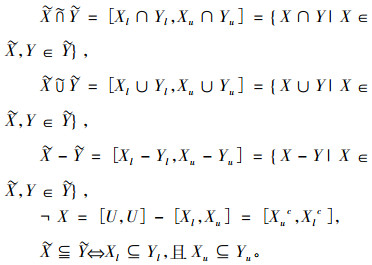
|
文献[15]将区间集理论与形式概念分析结合,在形式背景(G, M, I)上, 定义了IP(G)与IP(M)之间的一对映射, 即对于任意的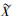
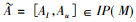
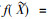

定义4[15] 设(G, M, I)为一个形式背景, 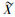
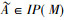
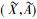
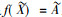
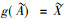
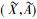
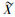
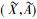
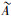
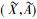
用IL(G, M, I)表示形式背景(G, M, I)上所有区间集概念的全体。设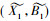
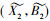
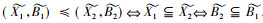
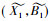
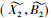
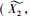
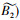
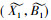
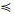
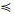
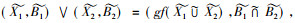
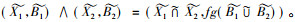
称完备格(IL(G, M, I), 
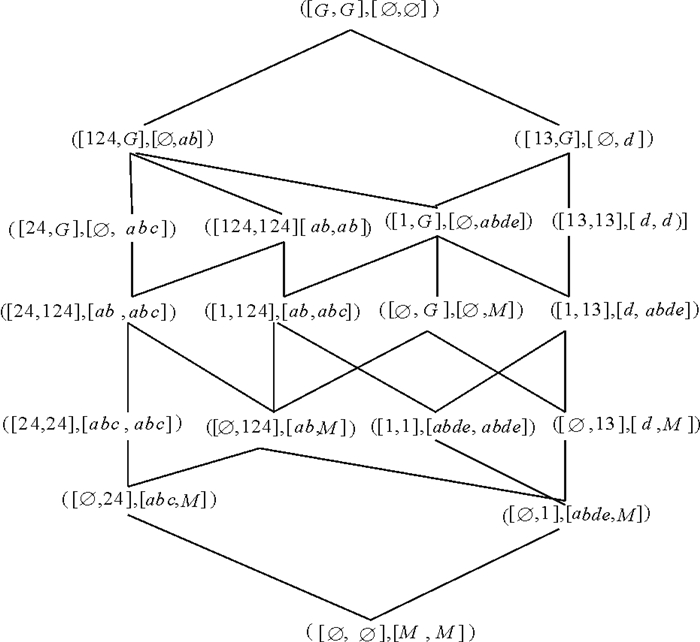
|
图 2 IL(G, M, I) Fig. 2 IL(G, M, I) |
由于区间集概念格的概念形成算子是由概念格中的概念形成算子给出的, 因此, 区间集概念与形式概念、区间集概念格与经典概念格有着必然的联系。本节从元素及代数结构上研究区间集概念格与经典概念格之间的关系。
定理1 设(G, M, I)为形式背景, L(G, M, I)及IL(G, M, I)分别为其经典概念格及区间集概念格, 则对于任意([X, Y], [B, A])∈IL(G, M, I), 都有(X, A), (Y, B)∈L(G, M, I)。
证明 因为([X, Y], [B, A])∈IL(G, M, I), 由区间集概念的定义知: f([X, Y])=[Y*, X*]=[B, A]且g([B, A])=[A*, B*]=[X, Y]。从而X*=A, Y*=B且A*=X, B*=Y。由形式概念的定义知:(X, A), (Y, B)∈L(G, M, I)。
例3 (续例1)由图 2所示, ([1, 124], [ab, abde])∈IL(G, M, I), 故根据定理1知(1, abde), (124, ab)∈L(G, M, I)。事实上, 通过图 1可验证这一结论。
反过来, 通过一个形式概念, 也可以构造出一个区间集概念, 如下定理所示。
定理2 设(G, M, I)为形式背景, L(G, M, I)及IL(G, M, I)分别为其经典概念格及区间集概念, 则对于任意(X, A)∈L(G, M, I), 都有([X, X], [A, A])∈IL(G, M, I)。进一步, 若(G, M, I)为正则的形式背景, 则对于任意(X, A)∈L(G, M, I), 都有如下结论成立:
([∅, X], [A, M]), ([X, G], [∅, A])∈IL(G, M, I)。
证明 因为(X, A)∈L(G, M, I), 所以由形式概念的定义知X*=A且A*=X。因而有f([X, X])=[X*, X*]=[A, A]且有g([A, A])=[A*, A*]=[X, X]。又由区间集概念的定义知([X, X], [A, A])∈IL(G, M, I)。
当(G, M, I)是正则的, 则∅*=M且M*=∅。从而有g([A, M])=[M*, A*]=[∅, X], 并且f([∅, X])=[X*, ∅*]=[A, M]。由区间集概念的定义知([∅, X], [A, M])∈IL(G, M, I)。同理可证([X, G], [∅, A])∈IL(G, M, I)。
事实上, 满足一定条件的两个不同形式概念也可以生成一个区间集概念。因此, 下面将定理2推广成如下定理。
定理3 设(G, M, I)为形式背景, L(G, M, I)及IL(G, M, I)分别为其经典概念格及区间集概念格。若(X, A)∈L(G, M, I), (Y, B)∈L(G, M, I), 且X⊆Y, 则([X, Y], [B, A])∈IL(G, M, I)。
证明 因为(X, A), (Y, B)∈L(G, M, I), 所以X*=A, A*=X且Y*=B, B*=Y。故有f([X, Y])=[Y*, X*]=[B, A]且g([B, A])=[A*, B*]=[X, Y]。又因为X⊆Y, 所以由算子*的性质知B⊆A。故[X, Y]∈IP(G)且[B, A]∈IP(M)。从而, 由区间集概念的定义知([X, Y], [B, A])∈IL(G, M, I)。
例4 (续例1)由图 1所示, (1, abde), (124, ab)∈L(G, M, I)且概念外延1⊆124, 故由定理3可知([1, 124], [ab, abde])∈IL(G, M, I)。事实上, 通过图 2可验证这一结论。
基于上述形式概念与区间集概念之间的关系, 我们将建立概念格与区间集概念格之间的关系。
定理4 设(G, M, I)为形式背景, L(G, M, I)及IL(G, M, I)分别为其经典概念格及区间集概念格。则存在一个映射h:L(G, M, I)→IL(G, M, I), 使得h(L(G, M, I))为IL(G, M, I)的一个子格。
证明 定义h:L(G, M, I)→IL(G, M, I), 对于任意的(X, A)∈L(G, M, I), 都有h((X, A))=([X, X], [A, A])。由定理2知([X, X], [A, A])∈IL(G, M, I)。显然h为L(G, M, I)到IL(G, M, I)的映射。因此h(L(G, M, I))是IL(G, M, I)的子集。
任取h((X, A)), h((Y, B))∈h(L(G, M, I)),按照h的定义及IL(G, M, I)中两元素上下确界的计算公式, 有h((X, A))∨h((Y, B))=([X, X], [A, A])∨([Y, Y], [B, B])= 
通过定理4的证明, 我们很容易知道存在的映射h是从L(G, M, I)到IL(G, M, I)的一个格同态。另外若(G, M, I)为正则形式背景, 则对于任意(X, A)∈L(G, M, I), 定义h((X, A))=([∅, X], [A, M])或者h((X, A))=([X, G], [∅, A]), 则其为L(G, M, I)到IL(G, M, I)的一个格同态。
3 区间集概念格的构造方法及其算法根据上一节关于概念格与区间集概念格之间的关系, 本节利用概念格的构造方法构造区间集概念格。
定理5 设(G, M, I)为形式背景, L(G, M, I)及IL(G, M, I)分别为其经典概念格及区间集概念格。则有:
IL(G, M, I)={([X, Y], [B, A])|(X, A), (Y, B)∈L(G, M, I)且X⊆Y}。
证明 为了书写方便, 记Δ={([X, Y], [B, A])|(X, A), (Y, B)∈L(G, M, I)且X⊆Y}。对于任意的([X, Y], [B, A])∈Δ, 由定理3知([X, Y], [B, A])∈IL(G, M, I)。从而很容易知Δ⊆IL(G, M, I)。反之, 对于任意的([X, Y], [B, A])∈IL(G, M, I), 由定理1知(X, A), (Y, B)∈L(G, M, I)。又因为[X, Y]为区间集, 所以由区间集的定义知X⊆Y。故Δ⊇IL(G, M, I)。综上所述Δ=IL(G, M, I), 即IL(G, M, I)={([X, Y], [B, A])|(X, A), (Y, B)∈L(G, M, I)且X⊆Y}。
事实上, 定理5给出了一种利用其概念格构造其相应区间集概念格的方法。下面, 给出这种方法的相应算法。
输入:形式背景(G, M, I)。
输出:区间集概念格IL(G, M, I)。
Step1.令IL(G, M, I)=∅。
Step 2.调用概念格求解算法Inclose2[20]计算概念格L(G, M, I)=Inclose2((G, M, I))。
Step 3. While((X, A), (Y, B)∈L(G, M, I))
{
If(X⊆Y)
{
IL(G, M, I)=IL(G, M, I)∪{([X, Y], [B, A])}
}
}
假设|G|, |M|, |L(G, M, I)|, 分别表示G, M, L(G, M, I)所含元素的个数。在算法中, Step 2利用Inclose 2[20]计算出了所有概念, 时间复杂度为O(|L(G, M, I)||G||M|2), Step 3是将概念转化成区间集概念的过程, 时间复杂度为O(|L(G, M, I)|2/2)。很容易发现算法的时间复杂度主要由Step 2以及Step 3提供。所以算法的时间复杂度是O(|L(G, M, I)||G||M|2+|L(G, M, I)|2/2)。
4 结语将问题简化研究是目前知识发现研究领域的一个重要手段。区间集概念格的构造理论研究亦不例外。作为形式概念分析的推广, 区间集概念格的研究尚处在起步阶段。我们针对区间集概念格的构造问题, 借助于概念格的构造理论提出了一种构造区间集概念格的方法, 此方法更为简洁地构造了区间集概念格。另外, 此内容的研究也将为更深一步的研究区间集概念格理论提供了一种具体的研究思路。例如区间集概念格的约简理论, 探讨是否可以通过概念格的约简直接寻找区间集概念格的约简等理论。
| [1] |
GAMTER B, WILLE R. Formal Concept Analysis:Mathematical Foundations[M]. New York: Springer-Verlag, 1999.
|
| [2] |
WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts[M]//Rival I(ed.), Ordered Sets.Reidel: Dordrecht-Boston, 1982: 445-470.
|
| [3] |
洪文学, 栾景民, 张涛, 等. 基于偏序结构理论的知识发现方法[J]. 燕山大学学报, 2014(5): 394-402. DOI:10.3969/j.issn.1007-791X.2014.05.004 |
| [4] |
JIANG G Q, CHUTE C G. Auditing the semantic completeness of SNOMED CY using formal concept analysis[J]. Journal of the American Medical Informatics Association, 2009, 16(1): 89-102. DOI:10.1197/jamia.M2541 |
| [5] |
KAYTOUE M, KUZNETSOV S O, NAPOLI A, et al. Mining gene expression data with pattern structures in formal concept analysis[J]. Information Sciences, 2011, 181(10): 1989-2001. DOI:10.1016/j.ins.2010.07.007 |
| [6] |
GANAPATHY V, KING D, JAEGER T, et al. Mining security sensitive operations in legacy code using concept analysis[M]//IEEE Computer Society, Proceedings of the 29th International Conference on Software Engineering. Minneapolis, MN: IEEE Computer Society, 2007: 458-467.
|
| [7] |
TONELLA P. Using a concept lattice of decomposition slices for program understanding and impact analysis[J]. IEEE Transactions on Software Engineering, 2003, 29: 495-509. DOI:10.1109/TSE.2003.1205178 |
| [8] |
DVNTSCH I, GEDIGA G. Modal-style operators in qualitative data analysis[M]//KUMAR V, TSUMOTO S, ZHONG N, et al.Proceedings of 2002 IEEE International Conference on Data Mining, Maebashi City: IEEE, 2002: 155-162.
|
| [9] |
YAO Y Y. Concept lattices in rough set theory[M]//DICK S, KURGAN L, PEDRYCZ W, et al.(Eds.).Proceedings of 2004 Annual Meeting of the North American Fuzzy Information Processing Society.Banff, Alberta, Canada: IEEE, 2004: 796-801.
|
| [10] |
MA J M, CAI M J. Concept acquisition approach of object-oriented concept lattices[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 123-134. DOI:10.1007/s13042-016-0576-1 |
| [11] |
QI J J, WEI L, YAO Y Y. Three-way formal concept analysis[M]//MIAO D, PEDRYCZ W, SLEZAK D, et al.(eds.), RSKT. Shanghai, China: Springer, 2014, 8818: 732-741.
|
| [12] |
QI J J, QIAN T, WEI L. The connections between three-way and classical lattices[J]. Knowledge-Based Systems, 2016, 91: 143-151. DOI:10.1016/j.knosys.2015.08.006 |
| [13] |
QIAN T, WEI L, QI J J. Constructing three-way concept lattices based on apposition and subposition of formal contexts[J]. Knowledge-Based Systems, 2017, 116: 39-48. DOI:10.1016/j.knosys.2016.10.033 |
| [14] |
刘琳, 钱婷, 魏玲. 基于属性导出三支概念格的决策背景规则提取[J]. 西北大学学报(自然科学版), 2016, 46(4): 481-487. |
| [15] |
徐伟华, 李金海, 魏玲, 等. 形式概念分析:理论与应用[M]. 北京: 科学出版社, 2016: 69-88.
|
| [16] |
YAO Y Y. Interval-set algebra for qualitative knowledge representation[M]//OSMAN A, CARL K C, WALDEMAR W K.Proceedings of the 5th International Conference on Computing and Information. Sudbury, Ontario, Canada: IEEE, 1993: 370-374.
|
| [17] |
YAO Y Y. Interval sets and three-way concept analysis in incomplete contexts[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 3-20. DOI:10.1007/s13042-016-0568-1 |
| [18] |
LI J H, MEI C L, LV Y J. Incomplete decision contexts:approximate concept construction, rule acquisition and knowledge reduction[J]. International Journal of Approximate Reasoning, 2013, 54(1): 149-165. DOI:10.1016/j.ijar.2012.07.005 |
| [19] |
魏玲, 万青, 钱婷, 等. 三元概念分析综述[J]. 西北大学学报(自然科学版), 2014, 44(5): 689-699. |
| [20] |
ANDREWS S. In-close2, a high performance formal concept miner[M]//ANDREWS S, POLOVINA S, HILL R, et al.(eds.). Conceptual Structures for Discovering Knowledge-Proceedings of the 19th International Conference on Conceptual Structures (ICCS).Derby, England: Springer, 2011: 50-62.
|
 2017, Vol. 47
2017, Vol. 47
