2. 昆明理工大学 理学院, 云南 昆明 650500
2. Faculty of Science, Kunming University of Science and Technology, Kunming 650500, China
概念格是以形式概念为元素并配备一个偏序关系得到的完备格。概念是在形式背景(U, A, I)基础上通过概念诱导算子构造产生的, 而概念诱导算子则由一对集值映射组成[1]:
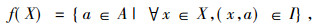
|
(1) |
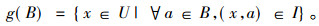
|
(2) |
其中X⊆U是对象子集, B⊆A是属性子集, (x, a)∈I表示对象x具有属性a。概念是形式概念分析理论中的基本知识单元[2]。需要指出的是, 定义概念的前提是概念诱导算子先满足保序伽罗瓦(Galois)连接或反序伽罗瓦连接。具体地, 映射φ:M→N与ϕ:N→M是偏序集M和N之间的保序伽罗瓦连接是指它们满足[3-4]:
(i) 任意m1, m2∈M, m1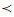
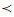
(ii) 任意n1, n2∈N, n1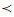
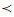
(iii) 任意m∈M, n∈N, ϕ(φ(m))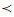
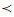
另一方面, φ与ϕ是偏序集M和N之间的反序伽罗瓦连接是指它们满足[2]:
(i) 任意m1, m2∈M, m1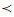
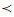
(ii) 任意n1, n2∈N, n1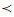
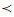
(iii) 任意m∈M, n∈N, m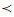
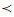
不难验证, 公式(1)与公式(2)定义的集值映射f和g是偏序集2U与2A之间的反序伽罗瓦连接, 其中2U是对象集U的幂集, 2A是属性集A的幂集。进一步还可以定义形式概念:对于X∈2U, B∈2A, 如果f(X)=B且g(B)=X, 则称序对(X, B)是一个形式概念(简称概念), 其中X和B分别称为概念的外延与内涵。概念之间的偏序关系约定为
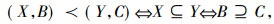
|
(3) |
那么所有概念连同上述偏序关系构成一个完备格, 称为概念格[1-2]。截止目前, 概念格研究已取得众多的研究成果, 比如概念格构造[5-8], 概念格规则提取[9-12], 概念三元格[13-15], 以及概念格与模糊集[16-18]、粗糙集[19-21]、粒计算[22-25]、认知计算[26-28]等的各种结合。
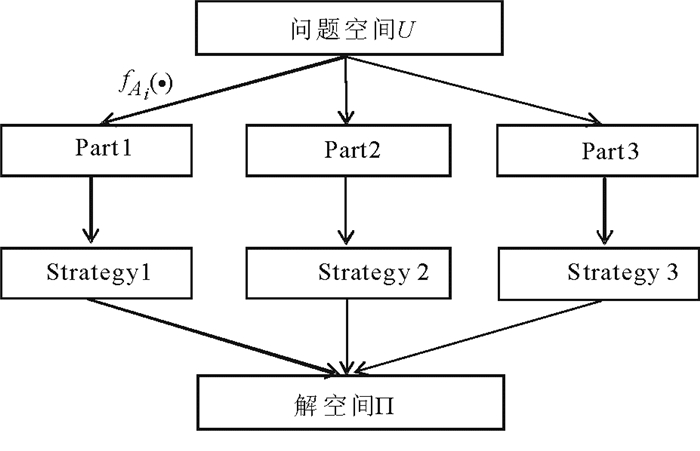
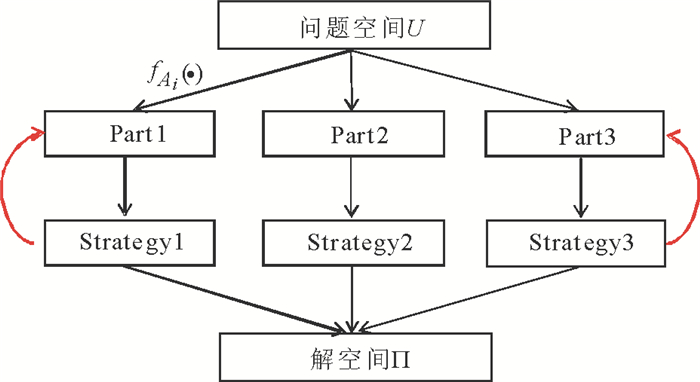
三支决策是姚一豫于2009年提出的以“三分而治(trisecting-and-acting)[29]”为主要思想的一个有效决策理论[30-31], 即将一个整体(论域)分为3个部分, 并采取有效的策略处理这3个部分。为了更好地论述三支决策理论处理问题的核心思想, 假设问题空间(即论域)为U, 问题描述评价函数为fAi(·)(即由属性子集Ai产生的函数), 三分结果为Part 1, Part 2, Part 3, 治略分别为Strategy 1, Strategy 2, Strategy 3, 并且解空间为Π, 那么图 1给出了三支决策理论解决问题的一般框架, 其中第1层(自上而下)为问题空间层, 第2层为三分结果层, 第3层为治略层, 第4层为解空间层。实际上, 整个框架充分体现了“分而治之”解决问题的基本思想。自顶而下相当于将整个问题子问题化, 通过分解模式解决问题; 自底而上相当于多策略局部优化, 最后逼近全局问题解。
|
图 1 三支决策解决问题的一般框架 Fig. 1 A general framework of three-way decisions solving problems |
另外, 需要指出的是, 图 1只是三支决策理论解决问题的一般框架, 实际中很多复杂问题涉及的“三分”与“治略”还需在一般框架的基础上继续延伸或扩展。比如, 三支决策理论中的序贯三支决策问题[32-33], “三分”与“治略”这两层就需要循环往复, 通常循环往复的原因是随着时间推移信息不断更新, 使得解决问题的约束条件在增加, 从而优化过程出现迭代致使目标结果更加具体, 此时三支决策解决复杂问题的扩展框架见图 2。与图 1相比, 图 2增加了“三分”层与“治略”层之间的循环往复(即整个这两层之间的循环往复), 也就是结合动态优化思想解决复杂问题[34], 它拓展了三支决策的具体应用范围。
|
图 2 三支决策解决复杂问题的扩展框架 Fig. 2 A generalized framework of three-way decisions solving complex problems |
三支决策理论中的3个决策, 通常被称为接受(Acceptance), 拒绝(Rejection), 不承诺(Non-commitment)[35]。接受域与拒绝域容易理解, 即根据现有信息能够作出接受或拒绝样本的明确选择, 但是不承诺相对难理解一些, 它实际上相当于延迟决策, 即根据现有信息无法明确判断样本到底属于接受域还是属于拒绝域, 为了避免误判或降低误判成本而暂时不得已选择延迟决策。这种情况下, 不承诺部分通常指的就是不确定域, 它由信息不完全或信息不足等因素导致的结果。所以, 三支决策理论也被一些学者视为是处理不确定性决策问题的有效方法[36-37], 并吸引了众多研究者的广泛关注[38-39]。
近年来, 概念格与三支决策的交叉融合研究受到有关学者的广泛重视。一方面, 人们将三支决策引入概念格中得到外延或内涵为论域或属性三分的三支概念, 有些具备共性属性与共性非属性同时分析的功能, 有些则具备描述缺失数据的功能, 它们共同增强了数据分析的效果; 另一方面, 把概念格引入三支决策中得到三支概念, 研究基于动态概念的三支决策, 使得序贯三支决策增加了特定的问题背景。目前, 概念格与三支决策相结合的研究已取得初步的研究成果, 下一节将展开详细介绍。此外, 本文还将给出概念格与三支决策相结合的研究展望, 对今后进一步开展相关工作提供一些参考。
1 概念格与三支决策相结合的研究历程及内容概念格与三支决策思想的结合可以追溯到1996年, 当然此时三支决策理论尚未提出, 所以仅仅只是三支决策思想的使用[40-41], 下面予以简单介绍:假设形式背景(U, A, I)的对象集(或样本空间)U根据观测数据被区分为正样本U+(Positive examples), 负样本U-(Negative examples)与不确定样本Uτ(Undetermined examples), 那么相应可获得正样本形式背景(U+, A, I+)(Positive contexts), 负样本形式背景(U-, A, I-)(Negative contexts)与不确定样本形式背景(Uτ, A, Iτ)(Undetermined contexts)。也就是, 论域U三分为正样本U+、负样本U-与不确定样本Uτ。在此基础上, 正样本被用来构建正假设(Positive hypothese), 负样本被用来构建负假设(Negative hypothese), 从而建立一个学习模型。实际上, 这里的学习模型相当于将形式背景的每个对象e∈U看作样本, 把形式背景的每个属性c∈A看作分类器, (e, c)∈I表示“分类器c匹配上样本e”。更多内容的介绍见文献[40-41]。
2009年Djouadi等[42]在不完全形式背景(U, A, {+, -, ?}, I)中通过最小完备化(将所有问号替换为符号“-”)与最大完备化(将所有问号替换为符号“+”), 提出了不确定概念(ill-known formal concept)((X*, X*), (B*, B*)), 其中(X*, B*)和(X*, B*)分别是最小完备化与最大完备化形式背景中的概念。这里的问号“?”代表缺失信息, 符号“+”代表对象肯定具有这个属性, 符号“-”代表对象肯定没有这个属性。2013年, 李金海等[43]在不完备形式背景中, 也使用三支决策思想描述缺失信息, 提出了近似概念(X, (B, C)), 其中X和(B, C)分别称为近似概念的外延与内涵。近似概念(X, (B, C))中的集合B表示X肯定具有的共性属性, 集合C表示X可能具有的共性属性。在这种情况下, 差集C-B表示不确定是否为共性属性, 补集~C表示X肯定不具有的共性属性。即B, C-B, ~C构成属性集A的三分结果。此外, 2017年姚一豫[44]对不完备形式背景的形式概念分析方法作了进一步研究, 利用区间集给出部分已知概念(Partially known concept), 它的外延由已知对象(Known objects), 已知非对象(Known non-objects), 以及状态未知对象(A set of objects with unknown states)组成。当然, 交换对象与属性的位置部分已知概念也是同样成立的。
2014年, 祁建军等[45]在形式背景(U, A, I)中提出三支概念, 三支概念这个词才开始正式使用。具体又细分为对象导出三支概念(X, (B, C))和属性导出三支概念((X, Y), B)。实际上, 对象导出的三支概念(X, (B, C))可以理解为对象集X把属性集A三分为B, C, A-B-C; 属性导出的三支概念((X, Y), B)类似地理解为属性集B把对象集U三分为X, Y, U-X-Y。不同于不完备形式背景下的不确定概念[42]、近似概念[43]、部分已知概念[44], 这里的三分思想的特征表现为“共同拥有的属性B”, “共同不拥有的属性C”, 其他属性A-B-C。实际上, “共同不拥有的属性”相当于补背景(U, A, 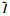
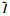
上述这些构造性方法在形式概念分析中实现三支决策统称为三支概念分析。根据三支决策的语义不同可以将三支概念分析区分为两类:完备形式背景中的三支概念分析[45-46], 不完备形式背景中的三支概念分析[42-44]。前者强调共性属性与共性非属性, 后者侧重缺失信息的近似描述。
除了三支概念分析, 概念格与三支决策还有另外一种结合模式, 称为三支概念学习[57]。不同于三支概念分析的构造性方法, 三支概念学习主要通过公理化方法将三支决策思想融入概念学习中。具体而言, 就是把三支决策的有关原理当作概念诱导算子H:2Q(A)→Τ(U), L:Τ(U)→2Q(A)的约束公理组[57], 这里Q(A)是属性集A的商集, 2Q(A)是商集Q(A)的幂集, Τ(U)是U的若干三支决策(X, Y)组成的集合。那么三支决策的有关原理融入概念诱导算子可叙述如下:
(a) 三支决策原理Ⅰ
知识越多, 作出的三支决策越精确(接受与拒绝增加, 不承诺减少), 即
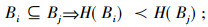
|
(4) |
(b) 三支决策原理Ⅱ
分小组作三支决策, 比整个大组作三支决策更有效, 即
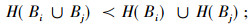
|
(5) |
(c) 三支决策原理Ⅲ
知识的选取, 由其诱导的三支决策是否与目标三支决策一致来确定, 即
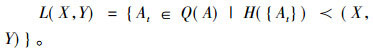
|
(6) |
满足上述三条公理的映射H:2Q(A)→Τ(U), L:Τ(U)→2Q(A)称为三支概念认知算子。三支概念认知算子的不动点((X, Y), B)称为三支概念。所谓三支概念学习, 是指在三支概念认知算子的基础上, 通过一定的学习方法从已知线索中获得新三支概念。而且, 到底获取什么样的三支概念, 需要用户事先指定三支概念认知算子的具体语义。此外, 由于三支概念学习往往涉及多源数据环境, 黄晨晨等[58]通过加权信息融合研究了多源数据环境下的三支概念学习, 并与单源数据下的三支概念学习作了对比分析, 阐述了加权信息融合的有效性。
下面, 在完备信息环境下, 讨论三支概念分析的三支概念((X, Y), B)与三支概念学习的三支概念((X′, Y′), B′)的区别。为了叙述方便, 引入两个图形象描述它们。图 3给出了三支概念分析下的三支概念((X, Y), B)的决策过程, 图 4给出了三支概念学习下的三支概念((X′, Y′), B′)的决策过程。从图 3可以看出, 三支概念分析下的三支概念((X, Y), B)的边界域U-X-Y随知识B的增加而增加, 原因是参与决策者越多共性对象越少, 这与完备信息环境下构造性方法研究三支决策时强调的“共同拥有”思想是一致的, 因为知识B的增加将带来数据不一致性变大, 所以达成“共同拥有”就越少。从图 4不难看出, 三支概念学习下的三支概念((X′, Y′), B′)的边界域U-X′-Y′随知识B′的增加而减少, 原因是参与决策者越多接受与拒绝就越多, 这与公理化方法研究三支决策时强调的“序贯三支决策”思想是一致的, 因为知识B的增加将导致上一轮不承诺的部分有可能重新启动作决策, 所以相对于之前的状态而言不承诺的部分将减少。所以, 三支概念分析下的三支概念((X, Y), B)与三支概念学习下的三支概念((X′, Y′), B′)在决策过程有较大差异。但是, 这两者并不矛盾, 因为三支概念分析下的三支概念从数据的一致性出发讨论三支决策, 那么共性属性越多满足的对象自然就越少; 而三支概念学习下的三支概念则通过公理化的方法承认“序贯三支决策”思想, 所以知识越多能够作出的接受与拒绝也就越多。
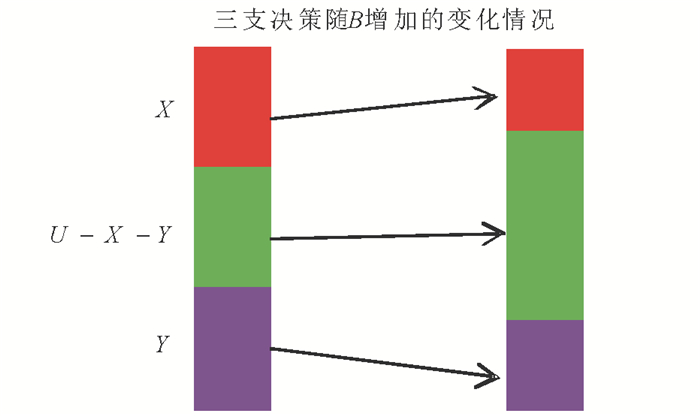
|
图 3 三支概念分析下的三支概念 Fig. 3 Three-way concept in three-way concept analysis |
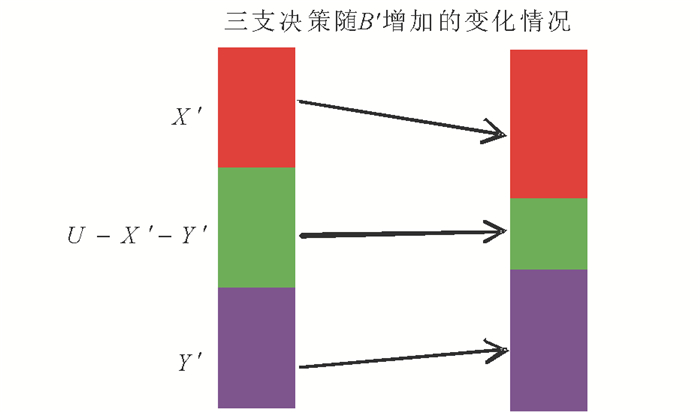
|
图 4 三支概念学习下的三支概念 Fig. 4 Three-way concept in three-way concept learning |
最后, 指出三支概念分析与三支概念学习在研究内容与目标方面的差异。类似于形式概念分析, 三支概念分析也可以开展三支概念格构造, 三支概念格约简与规则提取, 三支概念格模型推广, 三支概念格决策方法等方面的有关研究。但是, 三支概念学习与形式概念分析则有所不同, 它侧重公理化方法, 三支概念学习算法, 三支概念的粒计算方法, 三支概念认知学习等方面的有关研究。三支概念分析的研究目标是通过三支概念格实现数据分析及其应用, 而三支概念学习的研究目标是建立三支概念学习理论与方法, 包括各种三支概念学习算法的提出, 三支概念学习语义解释, 以及面向大数据的智能认知学习等。
2 概念格与三支决策相结合的研究展望本节介绍概念格与三支决策相结合的一些挑战性问题, 分别从三支概念分析与三支概念学习两个角度展开扼要论述。
2.1 三支概念分析中的挑战性问题三支概念分析从三支概念格构造、属性约简与规则提取以及模型比较等方面已作了初步研究[42-45, 56, 59], 下面给出需要进一步研究的问题。
2.1.1 各种三支概念之间的比较根据第1节的讨论, 三支概念分析可进一步区分为完备形式背景下的三支概念分析[45-46]与不完备形式背景下的三支概念分析[42-44]。它们的语义是不同的, 前者强调共性属性与共性非属性, 后者侧重缺失信息的近似描述。不完备形式背景下的三支概念分析目前有三种模型, 即不确定概念模型[42], 近似概念模型[43]以及部分已知概念模型[44]。那么, 比较分析这些三支概念模型之间的异同是非常有意义的。
2.1.2 三支概念之间的相似性度量三支概念之间的相似性度量是三支概念分析中的基本问题, 这方面的研究将带来概念合并与格结构的进一步简化。但是, 与经典概念之间的相似性度量[60]有所不同, 三支概念一方面由于边界域带来的数据不一致性, 使相似性度量方法的设计变得困难; 另一方面像模糊值或缺失值环境下的不确定性因素, 也会增加获取有效的相似性度量方法的难度。
2.1.3 多源数据的三支概念格构造三支概念格目前主要针对单源数据进行构建, 对于多源数据尚未见有关报道。类似地, 多源数据的三支概念格一般也是基于信息融合思想实现的, 但是它与普通的并行算法加速概念格构造有所不同, 因为普通并行算法只加快建格速度, 它并不影响最终计算结果。但是, 基于信息融合的多源数据的三支概念格构造, 它的最终结果会受信息融合函数选取的影响。也就是, 选择不同的信息融合函数, 得到的三支概念格结果可能是不同的。另外, 多源数据如果各个数据源之间存在属性重叠时, 会给信息融合函数的设计带来一定的困难。当然, 这些都是有待深入研究的细节问题。需要指出的是, 它们有时还与问题背景有一定的关系, 比如信息融合函数的权重选取通常与问题背景有关。
2.1.4 复杂数据的三支概念格构造完备信息环境下三支概念格的核心思想是对象与属性之间的“共同拥有”与“共同不拥有”关系, 但是对于复杂数据, 比如实值、模糊值、区间值的形式背景, 对象与属性之间的“共同拥有”与“共同不拥有”关系就不是很直观。换句话说, 实值, 模糊值, 区间值这类形式背景, 它们的补背景是不容易确定的。那么, 此时如何将三支决策思想融入概念格定义相关的三支概念格就变得困难。当然, 这类问题也是可以研究的, 尽管实值、模糊值、区间值属性不容易被三分, 但是对象集论域还是一样容易被三分的。这类形式背景的三支概念格模型具有很强的实用背景, 值得深入研究与分析。
2.1.5 三支概念格的优越性类似于三支决策[61], 三支概念格的优越性阐述也是非常重要的一个研究内容。从第1节回顾概念格与三支决策相结合的现有工作来看, 三支概念格具有其优越性。比如, 祁建军等[46]在研究经典概念格与三支概念格的关系中指出:三支概念格可以通过原背景的概念格与补背景的概念格联合构造, 而且还不是简单地把元素进行取并。也就是, 它们之间并不等价。这说明, 三支概念格与现有的正样本形式背景的概念格[40], 负样本形式背景的概念格[41], 或者正属性、负属性的混合概念格[55], 应该都有差异。那么这些差异的明确化, 将完全有可能阐述清楚三支概念格的优越性。
2.2 三支概念学习中的挑战性问题三支概念学习尽管也已经开展了一些研究, 包括三支概念学习的认知原理, 认知计算系统, 认知过程模拟, 以及面向多源数据的三支概念信息融合[57-58, 62]。但是, 仍有一些挑战性的问题需要突破, 下面逐一予以阐述。
2.2.1 具有容错功能的三支概念学习图 5给出了三支概念学习下的三支概念((X′, Y′), B′)随知识B′不断增加其对应三支决策的变化情况, 可以看出在整个三支决策过程中, 接受域与拒绝域是不断增加的, 而不承诺部分逐渐减少, 且是单调变化的。在认知无噪声的情况下, 这是非常漂亮的分析结果。然而, 现实中认知学习往往受噪声影响, 假设噪声在三支决策的某个阶段加入, 见图 5中“加入噪声”, 此时接受域、拒绝域、边界域的单调性会受到破坏(接受部分可能出现拒绝或不承诺, 拒绝部分也可能出现接受或不承诺), 如何解决噪声影响下的三支概念学习将是一个非常有意义的课题。
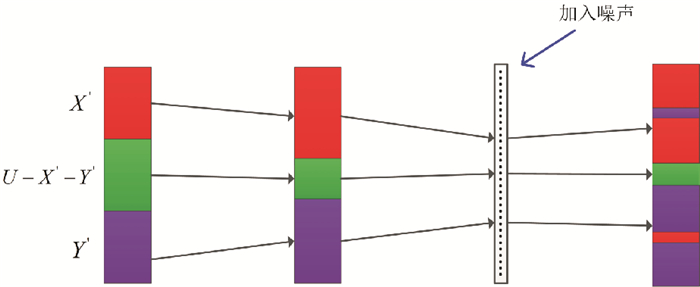
|
图 5 三支决策随B′增加的变化情况 Fig. 5 Changes of three-way decisions in case of B′ updating |
渐进式认知功能对于三支概念学习也是非常重要的, 所谓渐进式认知是指三支决策如何逐步识别出对应的属性知识。具体地, 在第1节的三支决策原理Ⅲ中, 识别三支决策(X, Y)对应的属性知识是一步到位的, 然而现实中这种识别关系是逐渐完成的, 也就是某些属性知识At被优先识别, 而另外一些属性知识As被延迟识别, 出现这种现象的原因是认知具有不完全性。到底哪些属性知识被优先识别, 哪些属性知识被延迟识别, 与个体偏好、背景知识以及先验知识等均有关。因此, 具有渐进式认知功能的三支概念学习问题, 其困难之处在于如何挖掘优先识别或延迟识别的内在规律。
2.2.3 异构数据环境下的三支概念学习图 6给出了针对异构数据的三支概念学习过程, 它大致可分为两个阶段:第1个阶段是异构数据各自获取三支决策, 第2个阶段是对各异构数据产生的三支决策结果进行信息集成, 以获取最终的三支决策。因此, 异构数据环境下的三支概念学习, 其核心问题是异构数据如何各自实现对象论域的三分?以及采取什么策略对各异构数据产生的三支决策结果进行有效的信息集成?值得一提的是, 智慧来[63]在异构形式背景下的概念格构造经验可以供研究此类问题时参考。
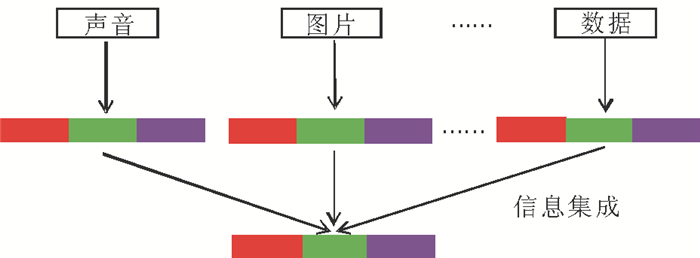
|
图 6 异构数据的三支决策 Fig. 6 Three-way decisions under heterogeneous data |
三支概念学习实际上是一种有效的概念认知计算方法[57], 三支决策则是利用三分而治模型(Trisecting-and-acting model)实现认知计算[29]。实际上, 无论是三支概念学习, 还是三支决策, 都可以与粒计算[64]相结合实现功能更强大的认知计算, 包括决策过程优化, 决策效率提高, 决策灵活性增强等方面。这将是今后值得深入开展的一个研究方向。
3 结语本文对概念格与三支决策相结合的研究历程、研究内容与研究展望作了扼要介绍, 有关论述与讨论并未详细展开, 只是力求能给读者展示一个新的研究方向, 以及这个研究方向中一些有价值也有难度的研究问题。特别地, 针对目前概念格与三支决策的两个结合点:三支概念分析和三支概念学习, 给予了对比分析, 说明它们之间并不矛盾, 只是从不同视角去结合三支决策而已, 即数据一致性导致的边界域与信息缺失或不足而引起的序贯三支决策导致的边界域, 属于不同的思维角度实现不同的分析目的。实际上, 数据一致性导致的边界域侧重概念格思维, 而信息缺失或不足而引起的序贯三支决策导致的边界域更多侧重三支决策思维。这两种思维是互补的, 能够发挥不同的研究作用。比如, 前者侧重概念格思维的三支概念, 与经典形式概念分析理论框架一致, 能够充分利用目前已提出的建格算法, 把更多注意力放到三支概念的理论与应用的突破上。后者侧重三支决策思维, 与经典三支决策理论一致, 能够从三支决策理论中的已有成果得到借鉴[65], 从而把更多注意力放到学习理论与方法的突破上, 特别是面向大数据的三支概念认知学习, 值得深入研究。
需要指出的是, 目前概念格与三支决策已开展的研究还不多, 不管是三支概念分析, 还是三支概念学习, 都处于初级研究阶段。比如, 三支概念分析目前还没有完全摆脱Wille概念格的研究思路, 三支概念学习也没有摆脱经典概念认知学习的研究方法, 这两个主要方向都需要提出更多有价值且有难度的研究问题, 特别是Wille概念格或经典概念认知学习没有触及到的问题, 不断挖掘这类问题才能逐渐开辟一个新的有前景的交叉融合研究方向。最后顺便指出, 有兴趣的读者, 还可以查阅徐伟华、李金海、邵明文和张文修[66]近期在International Journal of Machine Learning and Cybernetics杂志上组织出版的专辑《Concept lattice and three-way decisions》, 以了解最新研究动态。
致谢
感谢加拿大里贾纳大学(University of Regina)姚一豫教授对本文初稿提出的宝贵意见与建议!
| [1] |
WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts [C]//RIVAL I (ed.), Ordered Sets. Reidel: Dordrecht-Boston, 1982: 445-470. https://link.springer.com/chapter/10.1007%2F978-94-009-7798-3_15
|
| [2] |
GANTER B, WILLE R. Formal Concept Analysis:Mathematical Foundations[M]. New York: Springer, 1999.
|
| [3] |
DAVEY B, PRIESTLEY H. Introduction to Lattices and Order[M]. Cambridge: Cambridge University Press, 2002.
|
| [4] |
MEDINA J. Relating attribute reduction in formal, object-oriented and property-oriented concept lattices[J]. Computers & Mathematics with Applications, 2012, 64(6): 1992-2002. |
| [5] |
智慧来, 智东杰, 刘宗田. 概念格合并原理与算法[J]. 电子学报, 2010, 38(2): 455-459. |
| [6] |
GUO L K, HUANG F P, LI Q G, et al. Power contexts and their concept lattices[J]. Discrete Mathematics, 2011, 311: 2049-2063. DOI:10.1016/j.disc.2011.04.033 |
| [7] |
张涛, 任宏雷, 洪文学, 等. 基于属性拓扑的可视化形式概念计算[J]. 电子学报, 2014, 42(5): 925-932. DOI:10.3969/j.issn.0372-2112.2014.05.014 |
| [8] |
ZOU L G, ZHANG Z P, LONG J. A fast incremental algorithm for constructing concept lattices[J]. Expert Systems with Applications, 2015, 42(9): 4474-4481. DOI:10.1016/j.eswa.2015.01.044 |
| [9] |
谢志鹏, 刘宗田. 概念格与关联规则发现[J]. 计算机研究与发展, 2000, 37(12): 1415-1421. |
| [10] |
梁吉业, 王俊红. 基于概念格的规则产生集挖掘算法[J]. 计算机研究与发展, 2004, 41(8): 1339-1344. |
| [11] |
LI J H, MEI C L, LV Y J. Knowledge reduction in real decision formal contexts[J]. Information Sciences, 2012, 189: 191-207. DOI:10.1016/j.ins.2011.11.041 |
| [12] |
翟岩慧, 李德玉, 曲开社. 决策蕴涵规范基[J]. 电子学报, 2015, 43(1): 18-23. DOI:10.3969/j.issn.0372-2112.2015.01.004 |
| [13] |
LEHMANN F, WILLE R. A triadic approach to formal concept analysis [C]//ELLIS G, LEVINSON R, RICH W, SOWA J F (eds.), ICCS, 1995, 954: 32-43. https://wenku.baidu.com/view/200c3f34852458fb760b5657.html
|
| [14] |
魏玲, 万青, 钱婷, 等. 三元概念分析综述[J]. 西北大学学报(自然科学版), 2014, 44(5): 689-699. |
| [15] |
TANG Y Q, FAN M, LI J H. An information fusion technology for triadic decision contexts[J]. International Journal of Machine Learning & Cybernetics, 2016, 7(1): 13-24. |
| [16] |
WANG L D, LIU X D. Concept analysis via rough set and AFS algebra[J]. Information Sciences, 2008, 178(21): 4125-4137. DOI:10.1016/j.ins.2008.07.004 |
| [17] |
KANG X P, LI D Y, WANG S G, et al. Formal concept analysis based on fuzzy granularity base for different granulations[J]. Fuzzy Sets and Systems, 2012, 203: 33-48. DOI:10.1016/j.fss.2012.03.003 |
| [18] |
SHAO M W, LEUNG Y, WANG X Z, et al. Granular reducts of formal fuzzy contexts[J]. Knowledge-Based Systems, 2016, 114: 156-166. DOI:10.1016/j.knosys.2016.10.010 |
| [19] |
YAO Y Y. Concept lattices in rough set theory [C]//DICK S, KURGAN L, PEDRYCZ W, et al (eds.), Proceedings of NAFIPS, 2004: 796-801. https://wenku.baidu.com/view/7c2b912d453610661ed9f408.html
|
| [20] |
仇国芳, 张志霞, 张炜. 基于粗糙集方法的概念格理论研究综述[J]. 模糊系统与数学, 2014, 28(1): 168-177. |
| [21] |
LI J H, REN Y, MEI C L, et al. A comparative study of multigranulation rough sets and concept lattices via rule acquisition[J]. Knowledge-Based Systems, 2016, 91: 152-164. DOI:10.1016/j.knosys.2015.07.024 |
| [22] |
WU W Z, LEUNG Y, MI J S. Granular computing and knowledge reduction in formal contexts[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(10): 1461-1474. DOI:10.1109/TKDE.2008.223 |
| [23] |
MA J M, ZHANG W X, LEUNG Y, et al. Granular computing and dual Galois connection[J]. Information Sciences, 2007, 177(23): 5365-5377. DOI:10.1016/j.ins.2007.07.008 |
| [24] |
ZHI H L, LI J H. Granule description based on formal concept analysis[J]. Knowledge-Based Systems, 2016, 104: 62-73. DOI:10.1016/j.knosys.2016.04.011 |
| [25] |
WEI L, WAN Q. Granular transformation and irreducible elements judgment based on pictorial diagrams[J]. IEEE Transactions on Cybernetics, 2016, 46(2): 380-387. DOI:10.1109/TCYB.2014.2371476 |
| [26] |
LI J H, MEI C L, XU W H, et al. Concept learning via granular computing:A cognitive viewpoint[J]. Information Sciences, 2015, 298: 447-467. DOI:10.1016/j.ins.2014.12.010 |
| [27] |
XU W H, LI W T. Granular computing approach to two-way learning based on formal concept analysis in fuzzy datasets[J]. IEEE Transactions on Cybernetics, 2016, 46(2): 366-379. DOI:10.1109/TCYB.2014.2361772 |
| [28] |
徐伟华, 李金海, 魏玲, 等. 形式概念分析理论与应用[M]. 北京: 科学出版社, 2016.
|
| [29] |
YAO Y Y. Three-way decisions and cognitive computing[J]. Cognitive Computation, 2016, 8(4): 543-554. DOI:10.1007/s12559-016-9397-5 |
| [30] |
YAO Y Y. Three-way decision: an interpretation of rules in rough set theory [C]//WEN P, LI Y, POLKOWSKI L, et al. RSKT, 2009, 5589: 642-649. http://www2.cs.uregina.ca/~yyao/PAPERS/rskt2009.pdf
|
| [31] |
YAO Y Y. Three-way decisions with probabilistic rough sets[J]. Information Sciences, 2010, 180: 341-35. DOI:10.1016/j.ins.2009.09.021 |
| [32] |
YAO Y Y. Granular computing and sequential three-way decisions [C]//LINGRAS P, WOLSKI M, CORNELIS C, et al.RSKT, 2013, 8171: 16-27. http://www2.cs.uregina.ca/~yyao/PAPERS/granular_computing_and_sequential_three-way_dcisions.pdf
|
| [33] |
LI H X, ZHANG L B, HUANG B, ZHOU X Z. Sequential three-way decision and granulation for cost-sensitive face recognition[J]. Knowledge-Based Systems, 2016, 91: 241-251. DOI:10.1016/j.knosys.2015.07.040 |
| [34] |
JIA X Y, TANG Z M, LIAO W H, SHANG L. On an optimization representation of decision-theoretic rough set model[J]. International Journal of Approximation Reasoning, 2014, 55(1): 156-166. DOI:10.1016/j.ijar.2013.02.010 |
| [35] |
YAO Y Y. An outline of a theory of three-way decisions [C]//YAO J T, YANG Y, SLOWINSKI R, et al. (eds.) RSCTC, 2012, 7413: 1-17. http://www2.cs.uregina.ca/~yyao/PAPERS/a_theory_of_three_way_decisions.pdf
|
| [36] |
YU H, JIAO P, YAO Y Y, et al. Detecting and refining overlapping regions in complex networks with three-way decisions[J]. Information Sciences, 2016, 373: 21-41. DOI:10.1016/j.ins.2016.08.087 |
| [37] |
YANG X P, YAO J T. Modelling multi-agent three-way decisions with decision theoretic rough sets[J]. Fundamenta Informaticae, 2012, 115: 157-171. |
| [38] |
LIU D, YAO Y Y, LI T R. Three-way investment decisions with decision-theoretic rough sets[J]. International Journal of Computational Intelligence Systems, 2011, 4(1): 66-74. |
| [39] |
LIANG D C, PEDRYCZ W, LIU D, et al. Three-way decisions based on decision-theoretic rough sets under linguistic assessment with the aid of group decision making[J]. Applied Soft Computing, 2015, 29: 256-269. DOI:10.1016/j.asoc.2015.01.008 |
| [40] |
KUZNETSOV S O. Mathematical aspects of concept analysis[J]. Journal of Mathematical Science, 1996, 80(2): 1654-1698. DOI:10.1007/BF02362847 |
| [41] |
KUZNETSOV S O. Complexity of learning in concept lattices from positive and negative examples[J]. Discrete Applied Mathematics, 2004, 142: 111-125. DOI:10.1016/j.dam.2003.11.002 |
| [42] |
DJOUADI Y, DUBOIS D, PRADE P. Differentes extensions floues de l′analyse formelle de concepts [C]//Proceedings of LFA, 2009: 141-148.
|
| [43] |
LI J H, MEI C L, LV Y J. Incomplete decision contexts:Approximate concept construction, rule acquisition and knowledge reduction[J]. International Journal of Approximate Reasoning, 2013, 54(1): 149-165. DOI:10.1016/j.ijar.2012.07.005 |
| [44] |
YAO Y Y. Interval sets and three-way concept analysis in incomplete contexts[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 3-20. DOI:10.1007/s13042-016-0568-1 |
| [45] |
QI J J, WEI L, YAO Y Y. Three-way formal concept analysis [C]//MIAO D Q, PEDRYCZ W, SLEZAK D, et al.RSKT, 2014, 8818: 732-741. https://www.researchgate.net/publication/283414581_Three-Way_Formal_Concept_Analysis
|
| [46] |
QI J J, QIAN T, WEI L. The connections between three-way and classical concept lattices[J]. Knowledge-Based Systems, 2016, 91: 143-151. DOI:10.1016/j.knosys.2015.08.006 |
| [47] |
QIAN T, WEI L, QI J J. Constructing three-way concept lattices based on apposition and subposition of formal contexts[J]. Knowledge-Based Systems, 2017, 116: 39-48. DOI:10.1016/j.knosys.2016.10.033 |
| [48] |
祁建军, 汪文威. 多线程并行构建三支概念[J]. 西安交通大学学报, 2017, 51(3): 116-121. |
| [49] |
REN R S, WEI L. The attribute reductions of three-way concept lattices[J]. Knowledge-Based Systems, 2016, 99: 92-102. DOI:10.1016/j.knosys.2016.01.045 |
| [50] |
刘琳, 钱婷, 魏玲. 基于属性导出三支概念格的决策背景规则提取[J]. 西北大学学报(自然科学版), 2016, 46(4): 481-487. |
| [51] |
张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京: 清华大学出版社, 2005.
|
| [52] |
魏玲, 祁建军, 张文修. 决策形式背景的概念格属性约简[J]. 中国科学:信息科学, 2008, 38(2): 195-208. |
| [53] |
LI M Z, WANG G Y. Approximate concept construction with three-way decisions and attribute reduction in incomplete contexts[J]. Knowledge-Based Systems, 2016, 91: 165-178. DOI:10.1016/j.knosys.2015.10.010 |
| [54] |
李美争, 王国胤. 三支近似概念格中基于对象-概念辨识矩阵的属性约简方法[J]. 控制与决策, 2016, 31(10): 1779-1784. |
| [55] |
RODRIGUEZ-JIMENEZ J M, CORDERO P, ENCISO M, et al. Negative attributes and implications in formal concept analysis[J]. Procedia Computer Science, 2014, 31: 758-765. DOI:10.1016/j.procs.2014.05.325 |
| [56] |
李磊军, 李美争, 解滨, 等. 三支决策视角下概念格的分析和比较[J]. 模式识别与人工智能, 2016, 29(10): 951-960. |
| [57] |
LI J H, HUANG C C, QI J J, et al. Three-way cognitive concept learning via multi-granularity[J]. Information Sciences, 2017, 378: 244-263. DOI:10.1016/j.ins.2016.04.051 |
| [58] |
HUANG C C, LI J H, MEI C L, et al. Three-way concept learning based on cognitive operators:An information fusion viewpoint[J]. International Journal of Approximate Reasoning, 2017, 83: 218-242. DOI:10.1016/j.ijar.2017.01.009 |
| [59] |
SINGH P K. Three-way fuzzy concept lattice representation using neutrosophic set[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 69-79. DOI:10.1007/s13042-016-0585-0 |
| [60] |
WANG L D, LIU X D. A new model of evaluating concept similarity[J]. Knowledge-Based Systems, 2008, 21: 842-846. DOI:10.1016/j.knosys.2008.03.042 |
| [61] |
YAO Y Y. The superiority of three-way decisions in probabilistic rough set models[J]. Information Sciences, 2011, 181: 1080-1096. DOI:10.1016/j.ins.2010.11.019 |
| [62] |
SHIVHARE R, CHERUKURI A K. Three-way conceptual approach for cognitive memory functionalities[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(1): 21-34. DOI:10.1007/s13042-016-0593-0 |
| [63] |
智慧来. 面向异构数据分析的形式概念分析扩展模型[J]. 电子学报, 2013, 41(12): 2451-2455. DOI:10.3969/j.issn.0372-2112.2013.12.020 |
| [64] |
ZADEH L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy Sets and Systems, 1997, 90(2): 111-127. DOI:10.1016/S0165-0114(97)00077-8 |
| [65] |
HU B Q. Three-way decisions space and three-way decisions[J]. Information Sciences, 2014(281): 21-52. |
| [66] |
XU W H, LI J H, SHAO M W, et al. Editorial[J]. International Journal Machine Learning and Cybernetics, 2017, 8(1): 1-2. DOI:10.1007/s13042-016-0600-5 |
 2017, Vol. 47
2017, Vol. 47