【主持人语】 形式概念分析理论是20世纪80年代由德国数学家Wille提出的一种数据分析理论。该理论以形式背景(由对象和属性组成的二维交叉表)为基础,从中提炼出形式概念,从而对哲学中的概念这一人类思维的基本单元进行了形式化表达,进一步又形成概念格这一核心数据结构,以进行知识的可视化表示。在形式概念分析中,通过对形式背景增加决策属性可得到决策形式背景,以此为基础可以研究决策规则获取并实现决策分析;若把形式概念的表现形式从经典集变为区间集,则可得到区间集概念这一新的数据表示方式,进而可提供对于概念知识的新理解与新解释,以及获取知识的新方法;三支决策是一种基于人类认知的决策模式,其思想普遍存在于生活的各个方面,把三支决策与形式概念分析相结合产生的三支概念分析就是一种新的进行数据分析和知识发现的新理论。此外,以形式背景扩展出的三元背景(由对象、属性和条件组成的三维交叉表)为基础的三元概念分析理论,是受实用主义哲学启发而提出的一种新的信息处理方法,是分析三维数据的新框架,对于形式概念分析理论的发展是一个很好的补充和完善。
本次专题针对形式概念分析理论中的一些重要问题进行研究,包括三元背景基于二元关系不变的约简,基于属性概念的决策形式背景协调性研究,区间集概念格的构造,以及概念格与三支决策的研究展望等四个方面的内容。这些工作有针对新问题的讨论,有对已有问题从新角度进行的重新认识,都将为形式概念分析理论的进一步研究打下基础。
主持人:魏玲,西北大学数学学院教授,博士生导师。
2. 西安电子科技大学 计算机学院,陕西 西安 710071
2. School of Computer Science & Technology, Xidian University, Xi′an 710071, China
形式概念分析(Formal Concept Analysis, FCA) [1-2]是德国数学家Wille R.于1982年提出的一种处理二维数据的重要理论与方法。近年来, 形式概念分析在构建概念格[3]、属性约简[4]以及规则提取[5]等方面已取得了诸多理论成果, 且形式概念分析的约简理论对复杂的二维数据在信息简化方面提供了理论依据。
受Peirce C.三个论域范畴的实用主义哲学[6]的影响, Wille R.等人又于1995年提出了一种新的数据处理方法:三元概念分析(Triadic concept analysis, TCA) [7-8]。该理论可用于处理三维数据, 可从三维数据集(对象、属性及条件)的三元关系中得到三元概念及其层次结构。由于三元概念分析相关理论较形式概念分析而言更加复杂, 因此三元概念分析的研究成果也较少。魏玲等人从概念三元格的构造[7-10]、三元蕴含及关联规则挖掘[11-13]、三元模态算子[14]、三元概念聚类[15-18]以及三元背景的因子分析[19-22]等角度对三元概念分析的现有研究工作进行了梳理总结, 使我们对三元概念分析有一个更全面的认识[23]。
随着信息时代的到来, 三维数据日益增多, 三元概念分析的应用更加广泛。为了简化三元概念分析中的知识发现过程及知识表示结果, 本文从属性约简的角度出发, 对三元背景中的三个论域同时进行约简, 以确定保持各个论域中二元关系不变的最小子背景; 进而讨论约简中不同类型元素的相关性质; 最后给出约简前后三元概念之间的关系。
1 三元概念分析基础知识三元概念分析中的基本概念与形式概念分析中类似, 包括三元背景, 诱导算子, 三元概念等。本节逐个给出。
定义1[7-8] 称(K1, K2, K3, Y)为一个三元背景, 其中K1={g1, …,gp}为对象集, 每个gi(i≤p)称为一个对象; K2={m1, …,mq}为属性集, 每个mj(j≤q)称为一个属性; K3={b1, …,br}为条件集, 每个bk(k≤r)称为一个条件; Y为K1, K2和K3之间的三元关系, Y⊆K1×K2×K3。若(g, m, b)∈Y, 则表示对象g在条件b下有属性m, 若(g, m, b)∉Y, 则表示对象g在条件b下不具有属性m。
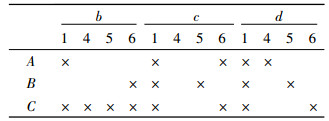
例1[7] 表 1是一个关于人物特点评价的三元背景(K1, K2, K3, Y)。其中对象集K1={A, B, C}表示不同的人物特点; 属性集K2={1, 2, 3, 4, 5, 6}给出了6种属性特征; 条件集K3={a, b, c, d}给出了4种条件。交叉符号表示分属于3个不同集合的相应元素具有三元关系Y。
|
|
表 1 三元背景(K1, K2, K3, Y) Tab. 1 A triadic context (K1, K2, K3, Y) |
三元概念分析中有两类诱导算子, (i)-诱导算子与(i, j, Xk)-诱导算子, 具体定义如下。
定义2[7-8] 设
X(i)={(aj, ak)∈Kj×Kk|(ai, aj, ak)∈Y, ∀ai∈Ki},
Z(i)={ai∈Ki|(ai, aj, ak)∈Y, ∀(aj, ak)∈Z}。
此类诱导算子实为经典形式背景
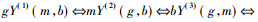
定义3[7-8] 设 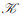
Xi(i, j, Xk)={aj∈Kj|(ai, aj, ak)∈Y, ∀(ai, ak)∈Xi×Xk},
Xj(i, j, Xk)={ai∈Ki|(ai, aj, ak)∈Y, ∀(aj, ak)∈Xj×Xk}。
此类诱导算子实为经典形式背景
(ai, aj)∈YXkij⇔∀ ak∈ Xk, (ai, aj, ak)∈Y。
由这两种诱导算子的定义及其与经典形式背景中算子的关系可知, 一个三元背景可看作是3个论域中两两之间关系所对应的三类形式背景的一种组合表示。其形式看似复杂, 本质上却比3类形式背景要简洁, 而所反映的信息一致。
利用这两类诱导算子可定义三元概念如下:
定义4[7] 设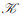
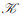
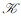
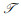

例2 例1中三元背景(K1, K2, K3, Y)的所有三元概念的集合
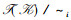
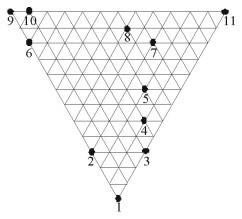
|
图 1 三元背景(K1, K2, K3, Y)的概念三元格 Fig. 1 The concept triadic lattice of (K1, K2, K3, Y) |
定义5 设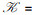
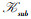
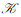
定义6 设
本节给出三元背景基于二元关系的约简的定义, 并依据约简将各个论域中的元素进行分类, 进而讨论不同类型的元素的性质。
2.1 约简的相关定义定义7 设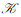
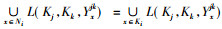
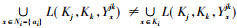
实际上, Ki的保持二元关系不变的约简保持了该论域中所有元素所对应的形式背景上的概念不变; 而同时对3个论域进行约简, 约简后得到的子背景即为原三元背景的约简背景。
定义8 设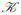
1) 核心元素集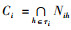
2) 相对可删除元素集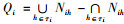
3) 绝对可删除元素集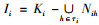
定理1 设(K1, K2, K3, Y)为有限的三元背景, 论域K1, K2, K3各自的约简必存在, 且约简背景必存在。
证明 若∀ai∈Ki, {i, j, k}={1, 2, 3}且i < j, 都有
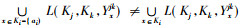
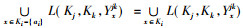
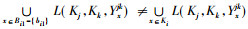
例3 续例1。固定K3中的每个元素, 所产生的形式概念如表 2所示。
|
|
表 2 K3中各个元素所对应的形式背景产生的形式概念 Tab. 2 Formal concepts corresponding to elements in K3 |
由定义7可知, a∈K3可被删除, 因为(K1, K2, Ya12)中的3个概念都可以从K3其他元素确定的形式背景获得; 且由定义8知, {a}为K3上的绝对可删除元素集合, {b, c, d}为K3上的核心元素集合。类似计算可知2, 3∈K2可被删除, {2, 3}为K2上的绝对可删除元素集合, {1, 4, 5, 6}为K2上的核心元素集合。因此, 原背景的约简背景为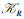
|
|
表 3 约简背景(K1, K2-{2, 3}, K3-{a}, Ynew) Tab. 3 The reduced triadic context (K1, K2-{2, 3}, K3-{a}, Ynew) |
该约简背景所有三元概念的集合为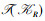

|
图 2 约简背景的概念三元格 Fig. 2 The concept triadic lattice of the reduced context |
我们对各个论域上的元素根据其在约简过程中的作用进行分类, 进而逐个研究其性质。
定义9 设(K1, K2, K3, Y)为三元背景, Ki(i=1, 2, 3)的所有约简为{Nih|h∈τi}, 记Qi为Ki上的相对可删除元素集, Ii为Ki上的绝对可删除元素集。对任意xi∈Qi, 称[xi]为Ki上xi的相对可删除类; 对任意xi∈Ii, 称[xi]为Ki上xi的绝对可删除类。
因此,结合定义6可知:相对可删除类就是相对可删除元素集合中元素的等价元素类, 绝对可删除类就是绝对可删除集中元素的等价元素类。
2.2.1 绝对可删除类的性质结合定义7及定义9, 我们可得到绝对可删除类的相关结论如下。
性质1 设(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且i < j, xi为Ki上的一个绝对可删除元素, [xi]为xi相应的绝对可删除类, 则
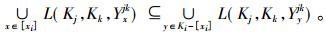
|
证明 设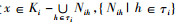
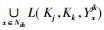
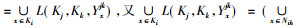
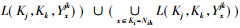

|
由定义9知, 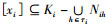
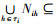

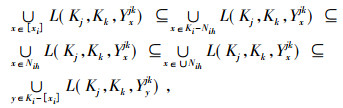
|
故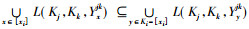
由性质1可知, 当xi为Ki上的绝对可删除元素时, 其对应的整个绝对可删除类[xi]对应的形式背景中的二元关系可由Ki中的其他元素所对应的形式背景的二元关系表示, 所以可将其全部删除。如例3中的绝对可删除元素a∈K3, 从表 2可以看出, (K1, K2, Ya12)的3个概念都可以从K3其他元素确定的形式背景获得, 且其相应的绝对可删除类仅它一个元素。进而由定义6知, 该xi所对应的形式背景产生的所有形式概念与[xi]所对应的形式背景产生的所有形式概念相同, 因此可得如下推论。
推论1 设(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且i < j, xi为Ki上的绝对可删除元素, [xi]为Ki上的绝对可删除类, ∀x∈[xi], 有

|
事实上, 绝对可删除类一般不止一个, 对于一个普通的绝对可删除元素而言, 我们结合定义6与定义9, 由推论1可得推论2。
推论2 设(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且i<j, Ki上的所有约简为{Nih|h∈τi}, 则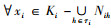
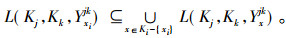
|
证明 因为
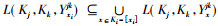
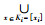
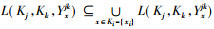
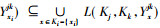
推论2表明, 当xi为Ki集合的绝对可删除元素时, 该元素所对应形式背景中的二元关系可由该论域中的其他元素所对应的形式背景中的二元关系表示。
例4 续例3, 由表 2知,
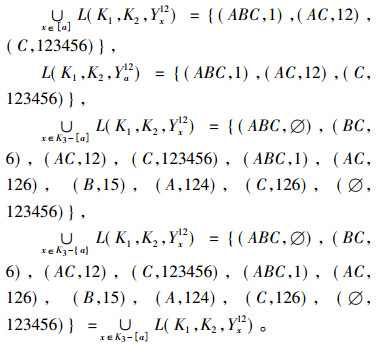
|
因此,

|
接下来, 我们给出相对可删除类的相关性质。
性质2 设(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且i < j, [xi]为Ki上的相对可删除类, Q为相对可删除元素集合, 则L(Kj, Kk, Yxijk) 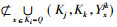
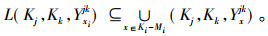
|
证明 由于[xi]⊆Nih-∩Nih且[xi]⊄Ki-∪Nih, 结合定义7, 有
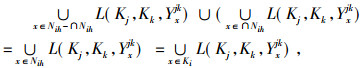
|
且
又因为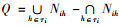
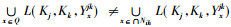
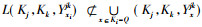
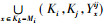
性质2表明, 当xi为相对可删除元素时, 不能完全删除集合[xi], 要至少保留[xi]中的一个元素, 才能保证原三元背景中所有的二元关系不变, 进而保证所有的形式概念不变。
2.2.3 非核心元素的性质由定义8知, 非核心元素集为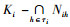
定理2 设(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且i<j, Ki上的所有约简为{Nih|h∈τi}, 则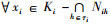
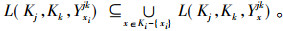
|
证明 设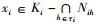
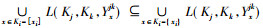
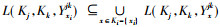
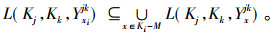
|
综上所述, 该定理得证。
定理2表明, 当xi为集合Ki的非核心元素时, 该元素所对应形式背景中的二元关系可由该论域中的其他元素所对应的形式背景中的二元关系来表示和反映; 自然地, 一个论域中任意非核心元素所对应形式背景中的概念一定是该元素所在论域约简后的其他元素所对应形式背景的某个概念。
推论3 设(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且i < j, Ki上的所有约简为{Nih|h∈τi}, 则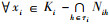

|
证明 由定理2知, 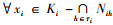
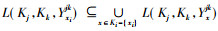
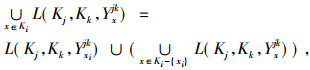
|
且由定义7知,
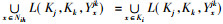
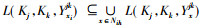
因此, 利用反证法, 可得到与推论3等价的性质。
性质3 设(K1, K2, K3, Y)为三元背景, Ki(i=1, 2, 3)上的所有约简为{Nih|h∈τi}, 则
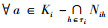
1) i=1, 即(a, y, z)∈Y时, 必有(a, y, z)=(b, y, z);
2) i=2, 即(x, a, z)∈Y时, 必有(x, a, z)=(x, b, z);
3) i=3, 即(x, y, a)∈Y时, 必有(x, y, a)=(x, y, b)。
证明 设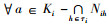
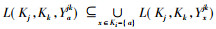
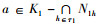
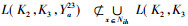
由2.2节知, 在对每一个论域进行约简时, 该论域约简前后所有元素所对应的形式背景的形式概念不变。本节我们考虑约简前后原三元背景与约简背景上的三元概念之间的关系。
定理3 设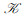
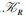
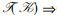
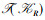
证明 记

|
(1) |

|
(2) |
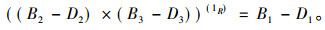
|
(3) |
证式(1):由于
((B1-D1)×(B2-D2))(3R)= {a3∈K3-D3|(a1, a2, a3)∈YR, ∀a1∈B1-D1, ∀a2∈B2-D2}= {a3∈K3|(a1, a2, a3)∈Y, ∀a1∈B1-D1, ∀a2∈B2-D2}-D3,
且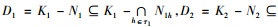
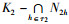
{a3∈K3|(a1, a2, a3)∈Y, ∀a1∈B1-D1, ∀a2∈B2-D2}={a3∈K3|(a1, a2, a3)∈Y, ∀a1∈(B1-D1)∪(B1∩D1), ∀a2∈B2-D2}={a3∈K3|(a1, a2, a3)∈Y, ∀a1∈(B1-D1)∪(B1∩D1), ∀a2∈(B2-D2)∪(B2∩D2)}={a3∈K3|(a1, a2, a3)∈Y, ∀a1∈B1, ∀a2∈B2}=B3,
故((B1-D1)×(B2-D2))(3R)=B3-D3。
同理可证式(2), (3)。
例5 由例2知(C, 126, abcd)∈ 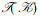
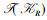
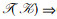

由定理3可知, 原来的三元概念在相应的维度上去掉D1, D2, D3后就是约简背景的三元概念。下面的定理4说明约简背景的三元概念是由原三元概念去掉D1, D2, D3之后产生的。
定理4 设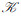

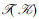
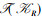
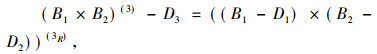
|
(4) |

|
(5) |
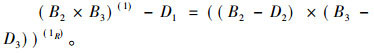
|
(6) |
证明 记删除集合D1后, 三元背景中的三元关系为YR1。
证式(4):因为
(B1×B2)(3)= {a3∈K3|(a1, a2, a3)∈Y, ∀a1∈B1, ∀a2∈B2}= {a3∈K3-D3|(a1, a2, a3)∈Y, ∀a1∈B1, ∀a2∈B2} ∪{a3∈D3|(a1, a2, a3)∈Y, ∀a1∈B1, ∀a2∈B2}。
又
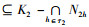
{a3∈K3-D3|(a1, a2, a3)∈Y, ∀a1∈B1, ∀a2∈B2}={a3∈K3-D3|(a1, a2, a3)∈YR1, ∀a1∈B1-D1, ∀a2∈B2}={a3∈K3-D3|(a1, a2, a3)∈YR, ∀a1∈B1-D1, ∀a2∈B2-D2}=((B1-D1)×(B2-D2))(3R)。
又由于{a3∈D3|(a1, a2, a3)∈Y, ∀a1∈B1, ∀a2∈B2}=(B1×B2)(3)∩D3, 因此, (B1×B2)(3)=((B1-D1)×(B2-D2))(3R)∪((B1×B2)(3)∩D3), 所以, (B1×B2)(3)-D3=((B1-D1)×(B2-D2))(3R), 式(4)得证。
同理可证式(5),(6)。
例6 由例2得, (C, 126, abcd)∈ 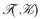
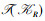
属性约简是FCA的重要研究方向之一, 但是在TCA中还没有相关研究。本文在TCA框架下, 提出了保持三元背景上所有二元关系不变的属性约简问题, 给出了各个论域中绝对可删除类、相对可删除类的相关性质; 研究了各个论域在属性约简前后概念格的关系; 最后, 获得了约简前后三元概念之间的关系, 即原三元概念删去可删除元素后可得到新三元概念, 新三元概念是由原三元概念删去可删除元素获得的。
FCA中的属性约简有很多不同的角度和意义, 后期, 针对三元背景, 也可以根据实际问题从不同角度出发发掘出有意义的约简, 进而对TCA框架下的属性约简问题进行较为深入的研究; 也可以将本文所提出的约简与其他约简进行比较, 探讨它们之间的关系。
主持人语
形式概念分析理论是20世纪80年代由德国数学家Wille提出的一种数据分析理论。该理论以形式背景(由对象和属性组成的二维交叉表)为基础,从中提炼出形式概念,从而对哲学中的概念这一人类思维的基本单元进行了形式化表达,进一步又形成概念格这一核心数据结构,以进行知识的可视化表示。在形式概念分析中,通过对形式背景增加决策属性可得到决策形式背景,以此为基础可以研究决策规则获取并实现决策分析;若把形式概念的表现形式从经典集变为区间集,则可得到区间集概念这一新的数据表示方式,进而可提供对于概念知识的新理解与新解释,以及获取知识的新方法;三支决策是一种基于人类认知的决策模式,其思想普遍存在于生活的各个方面,把三支决策与形式概念分析相结合产生的三支概念分析就是一种新的进行数据分析和知识发现的新理论。此外,以形式背景扩展出的三元背景(由对象、属性和条件组成的三维交叉表)为基础的三元概念分析理论,是受实用主义哲学启发而提出的一种新的信息处理方法,是分析三维数据的新框架,对于形式概念分析理论的发展是一个很好的补充和完善。
本次专题针对形式概念分析理论中的一些重要问题进行研究,包括三元背景基于二元关系不变的约简,基于属性概念的决策形式背景协调性研究,区间集概念格的构造,以及概念格与三支决策的研究展望等四个方面的内容。这些工作有针对新问题的讨论,有对已有问题从新角度进行的重新认识,都将为形式概念分析理论的进一步研究打下基础。
主持人:魏玲,西北大学数学学院教授,博士生导师。
| [1] |
GANTER B, WILLE R. Formal Concept Analysis:Mathematical Foundations[M]. New York: Springer-verlag, 1999.
|
| [2] |
WILLE R.Restructuring lattice theory: An approach based on hierarchies of concepts[C]//RIVAL I, ed.Ordered Sets.Reidel: Dordrecht-Boston, 1982: 445-470.
|
| [3] |
YAO Y Y. Concept lattices in rough set theory [C]//DICK S, KURGAN L, PEDRYCZ W and REFORMAT M (Eds.), Proceedings of 2004 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS 2004).New York: IEEE, 2004: 796-801.
|
| [4] |
张文修, 魏玲, 祁建军. 概念格的属性约简理论与方法[J]. 中国科学E辑:信息科学, 2005, 35(6): 628-639. |
| [5] |
张清华, 王国胤, 刘显全. 基于最大粒的规则获取算法[J]. 模式识别与人工智能, 2012, 25(3): 388-396. DOI:10.3969/j.issn.1003-6059.2012.03.005 |
| [6] |
PEIRCE C S. Collected Papers[M]. Cambridge: Harvard University Press, 1931-1935.
|
| [7] |
WILLE R. The basic theorem of triadic concept analysis[J]. Order, 1995, 12(2): 149-158. DOI:10.1007/BF01108624 |
| [8] |
LEHMANN F, WILLE R. A triadic approach to formal concept analysis [M]//ELLIS G, LEVINSON R, RICH W, et al. Conceptual Structures: Applications, Implementation and Theory (LNCS954). Heidelberg: Springer, 1995: 32-43.
|
| [9] |
BIEDERMANN K. Triadic Galois connections [M]//DENECKE K, LUDERS O. General Algebra and Applications in Discrete Mathematics. Aachen: ShakerVerlag, 1997: 23-33.
|
| [10] |
BIEDERMANN K. An equational theory for trilattices[J]. Algebra Universalis, 1999, 42(4): 253-268. DOI:10.1007/s000120050002 |
| [11] |
BIEDERMANN K. How triadic diagrams represent conceptual structures [M]//LUKOSE D, DELUGACH H, KEELER M, et al.International Conference on Conceptual Structures: Fulfilling Peirce′s Dream(LNCS1257). Heidelberg: Springer, 1997: 304-317.
|
| [12] |
GANTER B, OBIEDKOV S A. Implications in triadic formal contexts [M]//WOLFF K E, PFEIFFER H D, DELUGACH H S. Conceptual Structures at Work (LNCS3127). Heidelberg: Springer, 2004: 186-195.
|
| [13] |
MISSAOUI R, KWUIDA L. Mining triadic association rules from ternary relations [M]//VALTCHEV P, JASCHKE R.International Conference on Formal Concept Analysis(LNCS6628). Heidelberg: Springer, 2011: 204-218.
|
| [14] |
DAU F, WILLE R. On the modal understanding of triadic contexis[M]//DECKER R, GAUL W. Classification and Information Processing at the Turn of the Millennium. Heidelberg: Springer, 2000: 83-94.
|
| [15] |
IGNATOV D, KUZNETSOV S, MAGIZOV R, et al. From triconcepts to triclusters [M]//KUZNETSOV S O, SLEZAK D, HEPTING D H, et al. Rough Sets, Fuzzy Sets, Data Mining and Granular Computing (LNCS6743). Heidelberg: Springer, 2011: 257-264.
|
| [16] |
GNATYSHAK D, IGNATOV D, SEMENOV A, et al. Gaining insight in social networks with biclustering and triclustering [M]//ASEEVA N, BABKIN E, KOZYREV O.Perspectives in Business Informatics Research (LNBIP128).Heidelberg: Springer, 2012: 162-171.
|
| [17] |
TRABELSI C, JELASSI N, YAHIA S. Scalable mining of frequent tri-concepts from folksonomies [M]//TAN P N, CHAWLA S, HO C K, et al.Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining(LNCS7302). Heidelberg: Springer, 2012: 231-244.
|
| [18] |
JELASSI M N, YAHIA S B, NGUIFO E M. A scalable mining of frequent quadratic concepts in d-folksonomies [EB/OL]. Cornell University Library, 2012. arXiv: 1212.0087v1 [cs.SI].
|
| [19] |
BELOHLAVEK R, VYCHODIL V. Factorzing three-way binary data with triadic formal concepts [M]//SETCHI R, JORDANOV I, HOWLETT R J, et al. Knowledge-Based and Intelligent Information and Engineering Systems (LNCS6276). Heidelberg: Springer, 2010: 471-480.
|
| [20] |
GLODEANU C. Factorization methods of binary, triadic, real and fuzzy data[J]. Studia Universitatis Babes-Bolyai, Informatica, 2011, 56(2): 81-86. |
| [21] |
BELOHLAVEK R, VYCHODIL V. Optimal factorization of three-way binary data using triadic concepts[J]. Order, 2013, 30(2): 437-454. DOI:10.1007/s11083-012-9254-4 |
| [22] |
GLODEANU C V.Tri-ordinal factor analysis [M]//CELLIER P, DISTEL F, GANTER B.Formal Concept Analysis (LNCS7880).Heidelberg: Springer, 2013: 125-140.
|
| [23] |
魏玲, 万青, 钱婷, 祁建军. 三元概念分析综述[J]. 西北大学学报(自然科学版), 2014, 44(5): 689-699. |
 2017, Vol. 47
2017, Vol. 47