2. 天津电力公司 城东供电公司, 天津 300250
2. Chengdong Subsidiary, State Grid Tianjin Electric Power Company, Tianjin 300250, China
IGBT模块是一种电压控制的MOS/双极复合型器件, 在电力变换控制领域得到了广泛应用[1]。研究发现, 变流器中功率半导体器件的故障率高达31%, 且因温度造成失效的概率最高, 约为55%[2-3]。实际控制及变流工况中, IGBT模块的功率循环强度、温度波动与模块的电热疲劳程度及退化水平之间具有非常密切的关系[4-5]。因此, 研究IGBT的结温测量与预测对提高功率半导体器件的可靠性具有十分重要的作用。
IGBT结温测量方法包括物理接触法[6-7]、红外成像法[8]、温敏参数法[9-12]以及电热耦合模型法[13-15]等。其中, 温敏参数法以其无接触、不需打开封装、精度较高等优点在结温测量中得到了广泛应用。常见的温敏参数包括饱和压降VCEsat、集电极电流IC、栅射极阈值电压VGEth、栅极开通延迟时间tdon等。研究表明IGBT在小电流(小于100mA)条件下, 饱和压降和结温具有比较好的线性关系[16], 但IGBT在工况下具有比较大的电流等级, 此时IGBT模块饱和压降和结温具有较为复杂的关系[17], 因此,需要建立模型以准确表达其关系, 从而进行结温预测。
本文从IGBT半导体物理机理和等效电路的角度研究了饱和压降VCEsat、集电极电流IC以及结温Tj之间的内在关系, 通过IGBT结温测试试验得到了三者之间的关系图, 并在实验室条件下建立了基于温敏参数法的结温预测模型。BP神经网络以其强大的非线性追踪、自适应、自学习能力被广泛用于负荷预测、故障诊断等各种领域[18-19]。因此, 本文建立了BP神经网络结温预测模型, 将BP神经网络推广到IGBT结温预测中来, 这一探索对IGBT模块的结温预测及可靠性分析有一定的启发意义。
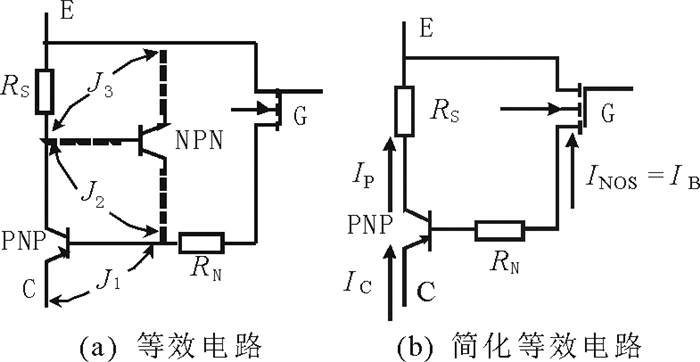
1 结温预测原理分析 1.1 饱和压降温敏特性研究混合型半导体器件IGBT等效为由单极型功率MOSFET和双极型晶体管PNP及NPN组成的电路, 其等效电路如图 1(a)所示。一般RS很小, 内部的NPN晶体管实际处于关闭状态, 简化等效电路如图 1(b)所示。图 1中, RS为P基区电阻, RN为PNP晶体管基区内的调制电阻, RN与IGBT的导通电阻密切相关。
|
图 1 IGBT芯片等效电路s Fig. 1 Equivalent circuit of IGBT chip |
由图 1可知IGBT的集电极电流IC及饱和压降VCEsat存在如下关系:
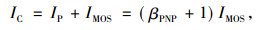
|
(1) |

|
(2) |
式(1)及式(2)中,VJ1为PNP晶体管EB结的导通压降; Rch为P型体区导通沟道电阻。
PNP部分的导通压降VPNP及MOSFET部分的导通压降VMOS分别为

|
(3) |

|
(4) |
由图 1知, IGBT结构的导通压降VCEsat等于PNP部分和MOSFET部分的压降之和,
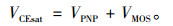
|
(5) |
式(3)至式(5)中,k为玻耳兹曼常量; T为绝对温度; q为电子的电荷量; WN为N型漂移区宽度; Da为双极扩散系数; ni为本征载流子浓度; p为元胞节距; Z为垂直于横截面方向上的元胞宽度; LCH为沟道长度; μni为反型层电子迁移率; COX为氧化层的特征电容; VG为栅偏压; VTH为阈值电压。式(3)中函数f(WN/2La)由下式给出, 其中VM为与通态压降相关的系数, La为双极扩散长度,
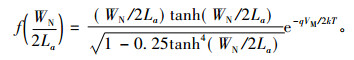
|
(6) |
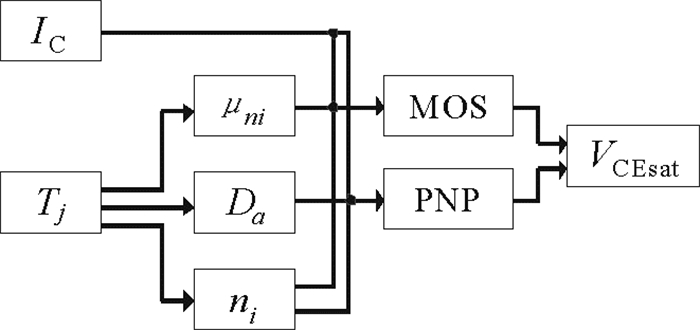
通过IGBT集射极饱和压降VCEsat模型式(3)至式(6)可以看出, 饱和压降受集电极电流IC、双极扩散系数Da等参数影响, 而其中部分是结温Tj的因变量, VCEsat影响因素逻辑关系如图 2所示。
|
图 2 VCEsat影响因素关系图 Fig. 2 Relation diagram of influencing factors of VCEsat |
由图 2可以看出, 结温Tj通过双极扩散系数Da、本征载流子浓度ni以及反型层电子迁移率μni直接对VCEsat的变化产生影响, 下面对这些温度相关的参数分别进行分析。
双极扩散系数的表达式为
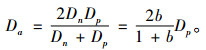
|
(7) |
其中,Dn为电子扩散系数, Dp为空穴扩散系数, b为双极迁移率, Dp和b的估算表达式分别为

|
(8) |

|
(9) |
将式(8)和式(9)代入式(7)可得
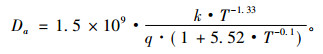
|
(10) |
由式(8)和式(9)可知, 空穴扩散系数Dp以及双极迁移率b均随温度的增大而减小, 其结果导致双极扩散系数Da随温度的增大而减小。
本征载流子浓度ni可由禁带宽度EG、导带NC和价带NV态密度表示为

|
(11) |
对于硅材料,
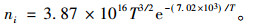
|
(12) |
根据式(11)和式(12)可知, 本征载流子浓度ni与温度的倒数成负相关关系。
反型层电子迁移率μni属于电子迁移率μn, μn用公式表示为

|
(13) |
由式(13)可知, 电子迁移率随温度的升高迅速减小。
综上所述, 集射极饱和压降VCEsat主要受到IC,Da,ni和μni的影响, 而其中Da,ni和μni由结温Tj决定, 即结温通过双极扩散系数Da、本征载流子浓度ni和反型层电子迁移率μni对饱和压降产生作用, 说明饱和压降和集电极电流是结温的参数, 可以表示为Tj=f′(VCEsat, IC)。
下文拟通过结温测试试验获取VCEsat,IC与Tj的相关数据, 依据数学模型以及BP神经网络模型发掘三者间的关系, 探索IGBT结温预测模型的建立方法。
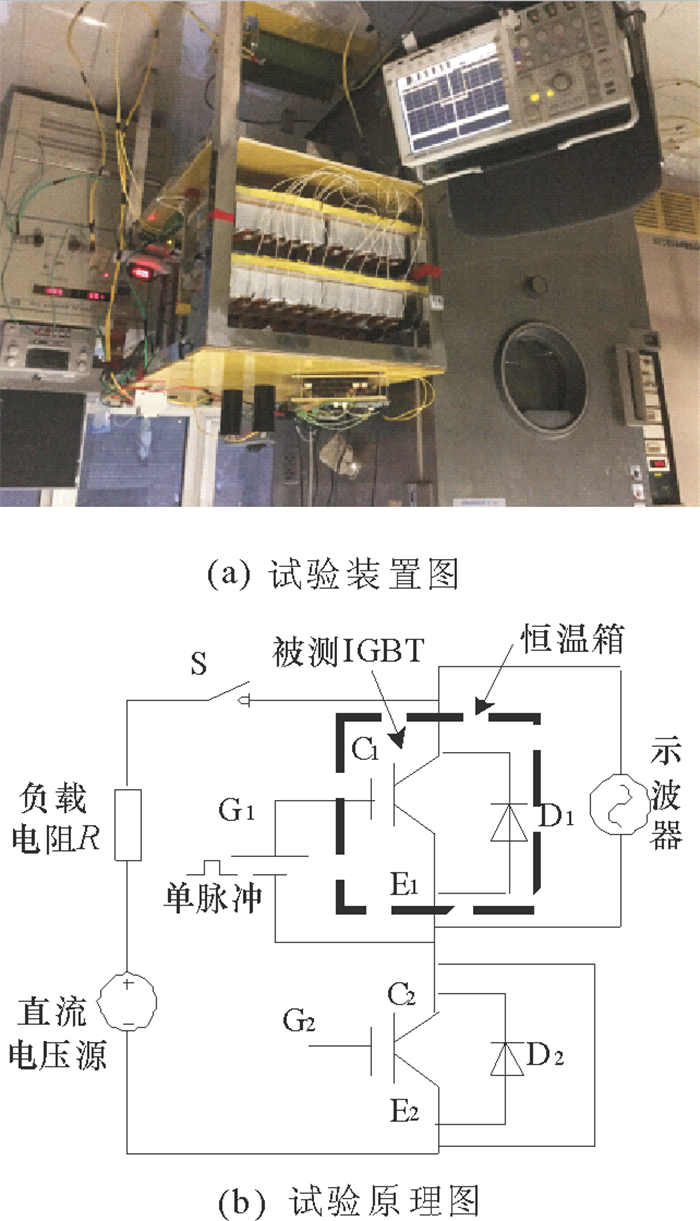
2 结温测试试验研究 2.1 结温测试试验与结果对1 200V/75A模块试品在不同集电极电流和结温下的饱和压降进行试验研究, 试验装置图和原理图如图 3所示。恒温箱调温范围可达-40℃~100℃; 调节直流电压源和负载, 可实现0~70A电流输出; 栅极驱动电路输出1ms单脉冲; 示波器经过16位高精度电压表校验。
|
图 3 试验装置图和原理图 Fig. 3 Test equipment and experimental schematic diagram |
根据GB/T29332-2012规定, IGBT模块集电极在小电流条件下时(≤100mA), 饱和压降和结温具有较好的线性关系。这是由于小电流条件下, IGBT模块自热不明显, 因此IGBT模块结壳无温差, 故此时认为结温等于壳温测量值。同理, 当短时大电流作用于IGBT模块集电极时, 只要无明显自热, 仍可将壳温测量值作为结温。试验研究表明, 驱动试品IGBT模块集电极通过额定及以下1ms脉宽电流时, 模块自热不明显, 结壳温差近似相等, 可以直接获取饱和压降和结温。因此, IGBT模块在通以适当脉宽集电极电流时, 也可研究饱和压降的温度特性。
首先, 将全新IGBT模块置于恒温箱中, 设定恒温箱的温度, 待IGBT模块达到热平衡后, 恒温箱温度即为结温。然后, 由栅极驱动模块在给定集电极电流下导通1ms, 同时示波器触发方式检测模块1ms内的饱和压降, 并记录数据。待IGBT模块再次达到热平衡后, 改变给定集电极电流, 重复此过程。为了更加清晰直观地分析结温、电流与饱和压降的关系,做出饱和压降VCEsat、结温Tj及集电极电流IC这三者不同形式的数据图, 如图 4所示。

|
图 4 VCEsat,Tj及IC不同形式的数据图 Fig. 4 Different forms of data graph among VCEsat, Tj and IC |
由图 4(a)可知, 集电极电流一定时, IGBT模块的饱和压降和结温具有一次函数关系, 当电流值约为20A时, 饱和压降VCEsat几乎不随结温变化, 称该点为温度系数零点, 对应的电流值20A称为临界电流。当集电极电流IC高于临界电流20A时, VCEsat为正温度系数, 反之为负温度系数。由图 4(b)可见, 任何结温下, IGBT模块的电流与饱和压降之间具有明显的非线性特征。
2.2 结温预测解析模型IGBT的结温Tj,饱和压降VCEsat与集电极电流IC之间的关系可以采用Tj=f′(VCEsat, IC)表示, 即基于饱和压降的温敏参数法结温预测模型。若直接对全部数据进行拟合分析, 则拟合误差较大, 相关系数为0.59, 因此根据临界电流值将数据分为两部分进行拟合分析。此时得到当IC低于临界电流时的最简结温拟合数学模型为
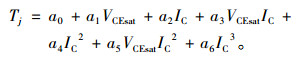
|
(14) |
其中,a0~a6为温度相关系数, 其拟合值范围列于表 1中。
|
|
表 1 a0~a6系数拟合值范围 Tab. 1 The fitting value range of a0~a6 |
同理, 当IC高于临界电流时的最简结温拟合数学模型为
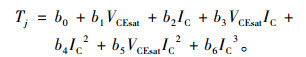
|
(15) |
其中,b0~b6为温度相关系数, 其拟合值范围列于表 2中。
|
|
表 2 b0~b6系数拟合值范围 Tab. 2 The fitting value range of b0~b6 |
根据拟合分析结果可知, 当IC低于临界电流时的相关系数为0.93, 当IC高于临界电流时的相关系数为0.98, 说明根据临界电流对数据进行分类运算可以明显提高结温预测的准确性。
根据以上最简结温拟合数学模型进行运算, 可以得到IC低于及高于临界电流时,温敏参数法部分拟合结果及其相对误差情况如表 3及表 4所示。其中所有结果近似取整数。可以发现, IC高于临界电流时的相对误差明显小于IC低于临界电流时, 且当IC低于临界电流时, 温度越低相对误差越大。
|
|
表 3 IC低于临界电流时温敏参数法部分拟合结果 Tab. 3 Part of the fitting results when IC is lower than the inflection point by temperature sensitive method |
|
|
表 4 IC高于临界电流时温敏参数法部分拟合结果 Tab. 4 Part of the fitting results when IC is higher than the inflection point by temperature sensitive method |
基于温敏参数法所建立的结温预测模型较好地表示了饱和压降VCEsat、集电极电流IC与结温Tj之间的非线性关系, 且模型预测精度较好。BP神经网络无需建立复杂的数学模型, 也无需了解任何器件内部的结构参数, 并且计算速度快, 计算精度高。为了更加快速准确地进行IGBT结温预测, 本文尝试使用BP神经网络对VCEsat和IC的数据进行训练, 从而进行结温预测。
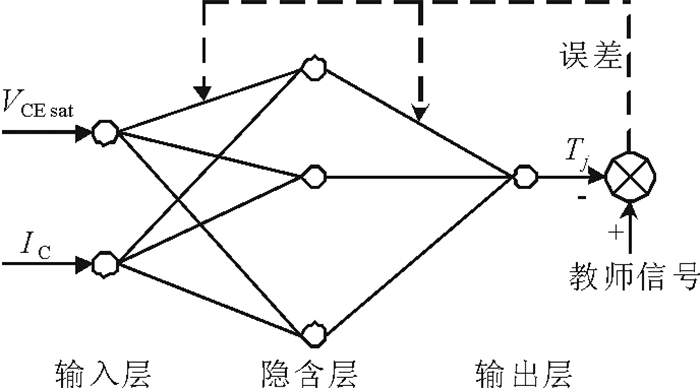
BP神经网络又称为反向传播网络, 是将W-H学习规则一般化, 对非线性可微分函数进行权值训练的多层网络。由于其结构简单, 算法清晰, 具有高精度、自适应、自学习的特点, 而广泛用于电力系统等各个领域。如图 5所示为BP神经网络的一种简单结构, 包括输入层、隐含层和输出层。本文选取BP神经网络的输入变量为饱和压降VCEsat与集电极电流IC, 输出变量为结温Tj, 在满足训练精度的前提下, 选取隐含层为3层。
|
图 5 一种BP神经网络的简单结构 Fig. 5 A simple structure of BP neural network |
至今使用BP神经网络进行结温预测的研究极少, 且训练数据量较少。因此, 本文采用大量试验数据, 以增加训练的准确性。已知所使用IGBT的临界电流值为20A, 为尽可能提高训练精度, 依据临界电流将试验数据分为两组, 其中低于20A的试验数据共52组, 高于20A的试验数据共130组。
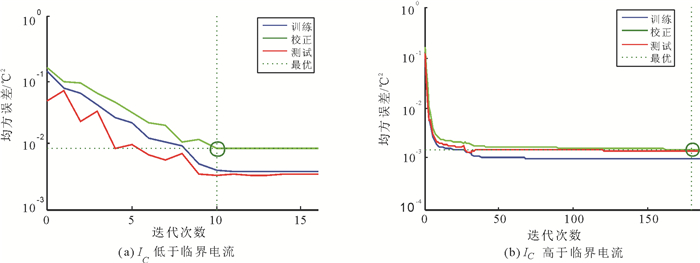
首先, 需对训练数据进行归一化处理, 避免发生过饱和。在BP神经网络训练过程中, 70%的数据用于训练, 15%的数据用于校正, 另外15%的数据用于测试。如图 6所示为BP神经网络建模过程中均方误差的变化曲线, 可以看出当IC低于临界电流时,BP神经网络算法迭代计算约10次,校正数据达到最佳均方误差,约为0.008℃2, 当IC高于临界电流时,约为180次达到最佳均方误差,约0.001℃2, 且高于临界电流时均方误差更小, 说明其拟合精度更高。由于数据量较大, 这里选取部分训练数据及训练结果, 如表 5及表 6所示。
|
图 6 BP神经网络训练均方误差变化曲线 Fig. 6 The mean squared error changing curve of BP neural network |
|
|
表 5 IC低于临界电流时的部分训练数据及结果 Tab. 5 Part of the training data and results when IC is lower than the inflection point |
|
|
表 6 IC高于临界电流时的部分训练数据及结果 Tab. 6 Part of the training data and results when IC is higher than the inflection point |
根据BP神经网络运算结果, IC低于临界电流时,其相关系数为0.981, IC高于临界电流时为0.996, 该值越接近1,则说明训练误差越小。结合表 5及表 6可知, 低于临界电流时的相对误差相较于高于临界电流时明显更大, 同样说明低于临界电流时非线性更明显。并且, 低于临界电流时, 低温度时的相对误差比高温度时更大; 高于临界电流时, 越接近于临界电流的相对误差越大。
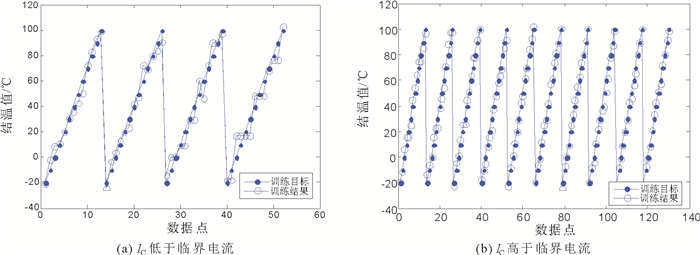
3.3 预测结果及分析图 7为IC低于及高于临界电流时BP神经网络法的预测结果。根据图 7可以发现, IC高于临界电流时, 预测结果更加接近训练目标, 而低于临界电流时, 有些点与训练目标存在一定误差。
|
图 7 BP神经网络法预测结果 Fig. 7 Prediction results of BP neural network method |
为了进一步验证BP神经网络的可行性与准确性, 对BP神经网络法与基于饱和压降的温敏参数法的结果进行对比分析。图 8所示给出了不同电流情况下,BP神经网络法与温敏参数法的相对误差对比图。由于当温度低于0度时, 温敏参数法及BP神经网络法的某些点相对误差过大, 说明在温度较低时,这两种模型并不适用, 故图 8仅给出温度在0度以上测试点的相对误差。低温下高精度的结温预测模型在未来应进行进一步的探索。

|
图 8 温敏参数法和BP神经网络相对误差对比图 Fig. 8 Comparison of relative error between temperature sensitive parameter method and BP neural network |
根据图 8可知, 低于临界电流时的相对误差值波动范围比高于临界电流时更大, 说明低于临界电流时非线性更明显。相比于温敏参数法, BP神经网络法图线的波动更小, 更加接近0相对误差线, 即所得相对误差绝对值更小, 由此说明了BP神经网络法进行结温预测将加快计算速度, 降低计算误差。
4 结语IGBT模块结温预测的发展趋势及目标是能够在工况下得以实施, 进而评估IGBT模块的热安全性。在实际工况中将本文研究设计的栅极驱动电路接入IGBT模块, 并使用测试设备测试所需数据, 即可使用本文所提出的基于饱和压降的结温预测模型进行结温预测。另外, 从BP神经网络角度提供一种IGBT模块结温预测的新思路, 由于BP神经网络使用计算机进行数据训练, 故其计算速度更快, 且通过对比分析证明其误差更小。
根据本文的理论分析、试验测试、温敏参数法建模过程及BP神经网络结温建模过程, 可以得到以下结论:
1) 通过对IGBT模块的饱和压降VCEsat、集电极电流IC与结温Tj的物理机理及试验测试数据结果的分析, 建立了基于饱和压降的温敏参数法IGBT结温预测模型。
2) 使用BP神经网络法对IGBT结温进行训练及建模, 根据临界电流将数据分为两组, 训练结果良好, 且高于临界电流时的误差比低于临界电流时小。
3) 对比分析BP神经网络法与温敏电参数法可知, BP神经网络预测绝对误差值更小, 更加接近0绝对误差线, 证明BP神经网络法相较于温敏参数法计算速度加快, 计算误差降低。
| [1] |
梅霜, 李志刚, 姚芳, 等. IGBT模块电气参数测试及分析[J]. 西北大学学报(自然科学版), 2016, 46(2): 184-187. |
| [2] |
YANG S, BRYANT A, MAWBY P, et al. An industry-based survey of reliability in power electronic converters[J]. IEEE Transactions on Industry Appfications, 2011, 47(3): 1441-1451. DOI:10.1109/TIA.2011.2124436 |
| [3] |
CHOI U, BLAABJERG F, LEE K. Study and handling methods of power IGBT module failures in power electronic converter systems[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2517-2533. DOI:10.1109/TPEL.2014.2373390 |
| [4] |
陈明, 胡安, 唐勇, 等. 绝缘栅双极型晶体管传热模型建模分析[J]. 高电压技术, 2011, 37(2): 453-459. |
| [5] |
MOROZUMI A, YAMADA K, MIYASAKAT, et al. Reliability of power cycling for IGBT power semiconductor modules[J]. IEEE Transactions on Industry Applications, 2003, 39(3): 665-671. DOI:10.1109/TIA.2003.810661 |
| [6] |
JU Y S, GOODSON K E. Thermal mapping of interconnects subjected to brief electrical stresses[J]. IEEE Electron Device Letters, 1997, 18(11): 512-514. DOI:10.1109/55.641429 |
| [7] |
张亚玲, 李志刚, 姚芳, 等. 一种IGBT热阻测试方法的研究[J]. 河北工业大学学报, 2016, 45(1): 1-4. |
| [8] |
DUPONT L, AVENAS Y, JEANNIN P O. Comparision of junction temperature evaluations in a power IGBT module using an IR camera and three thermosensitive electrical parameters[J]. IEEE Transactions on Industry Applications, 2013, 49(4): 1559-1608. |
| [9] |
CASTELLAZZI A, MERMET-GUYENNET M, BARLINI D, et al. New technique for the measurement of the static and of the transient junction temperature in IGBT devices under operating conditions[J]. Microelectronics Reliability, 2006, 46(9): 1772-1777. |
| [10] |
STRAUSS B, LINDEMANN A. Measuring the junction temperature of an IGBT using its threshold voltage as a temperature sensitive electrical parameter (TSEP)[C]//The 13th International Multi-Conference on Systems, Signals & Devices (SSD). Leipzig: IEEE, 2016: 459-467. http://ieeexplore.ieee.org/document/7473664/
|
| [11] |
BUTRON CCOA J A, STRAUSS B, MITIC G, et al. Investigation of temperature sensitive electrical parameters for power semiconductors (IGBT) in real-time applications[C]//International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management.Nuremberg: PCIM, 2014: 1-9. http://ieeexplore.ieee.org/document/6841269/
|
| [12] |
BAKER N, MUNK-NIELSEN S, IANNUZZO F, et al. Experimental evaluation of IGBT junction temperature measurement via peak gate current[C]//The 17th European Conference on Power Electronics and Applications.Geneva: CERN, 2015: 1-11. http://ieeexplore.ieee.org/abstract/document/7311733/
|
| [13] |
CASTELLAZZI A, CIAPPA M, FICHTNER W, et al. Electro-thermal model of a high-voltage IGBT module for realistic simulation of power converters[C]//The 37th European Solid State Device Research Conference. Munich: TUM, 2007: 155-158. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4430902
|
| [14] |
SHENG K, WILLIAMS B W, FINNEY S J. A review of IGBT models[J]. IEEE Transactions on Power Electronics, 2000, 15(6): 1250-1266. DOI:10.1109/63.892840 |
| [15] |
AMMOUS A, GHEDIRA S, ALLARD B, et al. Choosing a thermal model for electrothermal simulation of power semiconductor devices[J]. IEEE Transactions on Power Electronics, 1999, 14(2): 300-307. DOI:10.1109/63.750183 |
| [16] |
COVA P, FANTINI F. On the effect of power cycling stress on IGBT modules[J]. Microelectronics Reliability, 1998, 38(6): 1347-1352. |
| [17] |
GHIMIRE P, PEDERSEN K B, TRINTIS I, et al. Online chip temperature monitoring using VCE-load current and IR thermography[M]//2015 IEEE Energy Conversion Congress and Exposition. Montreal, Canada: IEEE, 2015: 6602-6609.
|
| [18] |
杨喆, 王家鼎, 谷天峰. 滑带黄土振陷预测中的BP神经网络方法[J]. 西北大学学报(自然科学版), 2007, 37(5): 815-818. |
| [19] |
JIA G, LI D, YAO L, et al. An improved artificial bee colony-BP neural network algorithm in the short-term wind speed prediction[C]//The 12th World Congress on Intelligent Control and Automation (WCICA).Guilin: IEEE, 2016: 2252-2255. http://ieeexplore.ieee.org/document/7578265/
|
 2017, Vol. 47
2017, Vol. 47





