能源与环境问题是人类面临的主要挑战之一, 因此越来越引起人们的关注。其中, 寻找可持续能源, 提高现有能源的利用率是当下各国政府和科研院所一致努力的方向。除了开发一系列新的清洁能源(如太阳能, 风能, 潮汐能, 生物能源等)[1], 提高现有能源的利用率(如LED照明, 磁制冷技术)[2], 以及改进能源转换技术, 是另一个近来备受关注的方向。工业生产与日常生活中, 能源的消耗都会带来很多废弃的热能, 例如汽车尾气、热电厂废热、锅炉排放废气等等。数据统计表明, 世界范围内超过60%的能源由于各种原因被浪费[3-4]。热电能源转换技术可以利用热电材料将废热直接转换为电能。高效可靠的热电材料的研发将有助于提高能源的利用效率及太阳能等能源的转换率, 并在能源需求的挑战中起到重要的作用[5]。因此, 热电能源转换技术已经成为科研界和工业界的一个主要研究方向[3]。
早在1821年, 德国科学家托马斯·约翰·塞贝克(Thomas Johann Seebeck)就对热电现象进行了研究:他首先观察到不同温度的两种不同金属的接触会产生电势差, 即塞贝克效应。20世纪50年代, 随着热电能源转换基础理论的建立, 热电材料得到了迅猛的发展。重掺杂的半导体作为一类优良的热电材料得到了广泛的重视。目前, Bi2Te3作为典型的热电材料已经具有了商业化应用[5]。同时由于热电材料的高可靠性及相对简单的器件构造, 其在空间开发中也具有广泛的应用[3]。
其间, 随着美国能源部的推动[5]以及相关理论发展[6-7], 热电材料又经历了一波新的高速发展。具体而言, 有两个看似不同的发展方向[5]:一个是寻找新的块状材料, 另一个是开发低维材料; 然而两个方向从微观机制上来说都是相同的, 即提高材料的电导率以及降低晶格热导率。本文中所谈的中子散射技术是研究晶格热导率的一个最直观手段。
本文的主要目的是介绍中子散射技术在热电材料研究中的应用。从对热电材料机理的简单介绍开始, 对相关中子散射技术进行一些必要的介绍,最后给出3个实例来说明中子散射技术在热电材料研究领域的重要性。
1 热电机理介绍热电效应起源于材料中可自由移动的载流子的导电、导热性质。当材料中存在温度梯度时, 载流子将会从热端向冷端扩散。这种载流子的移动和集聚会在材料引入净电荷和电势场, 最终在相关化学势和静电势之间达到一个平衡态, 即塞贝克效应。这就是热电发电的物理基础[8]。
尽管热电器件的转换效率受限于卡诺效率[1, 9], 提高其性能却有很大的发展空间。热电器件的性能一般用材料的热电优值(Figure-of-merit, zT)来描述。zT是一个无量纲参数, 定义为[10]:
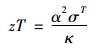
|
(1) |
其中α为塞贝克系数, σ为电导率, T为绝对温度, κ为热导率。
因此, 通过不断提高材料的塞贝克系数α和电导率σ, 以及降低材料的热导率κ可以提高材料的热电性能。例如, 塞贝克系数α是单位温度梯度下产生的电动势, 因此大的塞贝克系数α和大的温度差可以导致大的电动势。然而因为这几个热电参数之间存在复杂的内在关联, 实际操作并非如此简单[10]:
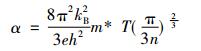
|
(2) |
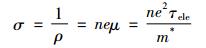
|
(3) |
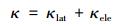
|
(4) |
其中kB为玻尔兹曼常数, n为载流子浓度, e载流子为单位电荷, h为普朗克常数, m*载流子有效质量, ρ为电阻率, μ为载流子迁移率, τele为载流子弛豫时间(即载流子寿命), κlat为晶格热导率, κele为电子热导率。
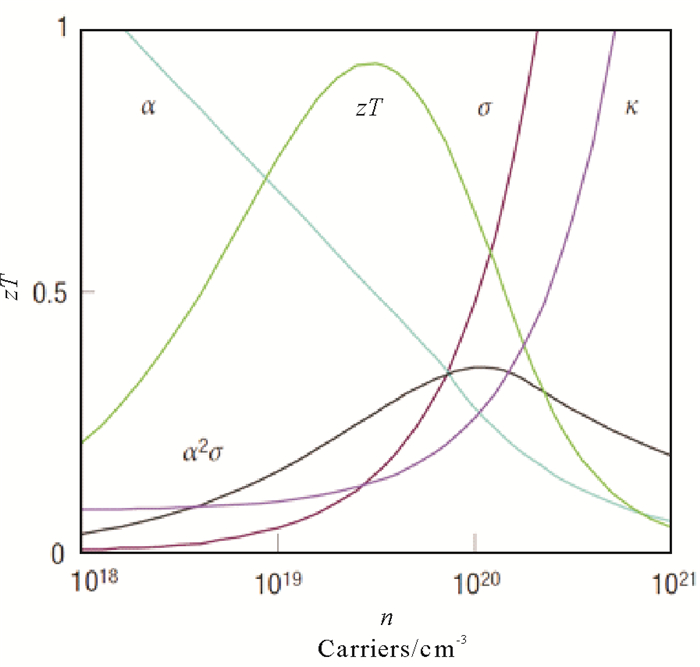
根据公式(2), 低载流子浓度的绝缘体或半导体会有比较大的塞贝克系数, 但是低载流子浓度意味着低的电导率(公式(3)); 同时, 公式(2)指出, 大的载流子有效质量有利于塞贝克系数的增加,但这样会降低载流子迁移率, 从而降低导电率。因此, 载流子浓度与有效质量必须在塞贝克系数和电导率之间进行平衡, 从而使α2σ(功率因数)最大化, 优化zT值。另一方面热电材料的热导率主要有两部分贡献, 电子和晶格热导率的贡献。根据维德曼-夫兰兹定理(Wiedemann-Franz law), 电导率的增长同样也会引起热导率的增长。为了优化zT值, 在电导率和热导率之间也同样需要需求平衡。如图 1所示, 各个热电参数之间的平衡关系对载流子浓度有很大依赖性。绝缘体和导体都不是热电材料的最佳选择, 而在重掺杂的半导体(载流子浓度n为1019~1021carriers/cm3)中一般可以找到最优zT值[11-12]。
|
图 1 通过改变Bi2Te3中载流子浓度优化热电参数[10, 13] Fig. 1 Dependence of thermoelectric parameters on charge carrier concentration |
如上所述, 从各个热电参数的相互关联关系上出发, 有两种优化热电zT值的途径, 即提高材料的功率因数α2σ和降低其晶格热导率κlat[1, 8]。
1.1 功率因数α2σ根据公式(2)和(3), 功率因数α2σ和载流子浓度n、有效质量m*、迁移率μ以及弛豫时间τele相关, 因此可以通过“能带结构工程”来优化zT值[14-25]。目前, 有很多不同的有效方法:通过改变化学成分的比例或加入额外的元素来破坏价键平衡, 从而改变载流子的浓度[26]; 通过掺杂改变电子态密度, 理论与实验均表明电子态密度的畸变可以增加载流子的有效质量, 从而提高塞贝克系数[1, 4], 例如在PbTe中掺杂Tl[16]和在SnTe中掺杂In[27]; 另一种提高功率因数α2σ的方法是调整材料中重价带和轻价带之间的能量偏差, 从而使能量相近的各种价带形成简并。这种方法不仅可以改变载流子的有效质量m*, 还可以提高其电导率σ[1, 4]。基于这种思想, 已经在Mg或Mn掺杂的PbTe[15, 20]以及空位掺杂的SnSe[25]中有效地提高了α2σ。还有一种方法称为“电子过滤”, 该方法可以使用异质结超晶格减弱塞贝克系数α和电导率σ之间的耦合, 从而提高功率因数α2σ[10, 28-29]。
1.2 声子(phonon)与晶格热导率(κlat)热电材料中的热导率主要有电子和晶格的贡献(公式(4))。维德曼-夫兰兹定理指出电子热导率κlat与温度T和电导率σ成线性正比关系。而晶格热导率来自于晶格热振动, 即声子(phonon)。在介绍晶格热导率之前, 简单复习一下有关声子的基本知识。
在经典力学中, 晶体中晶格热振动可以描述为典型的小振动问题。热振动带来的相对于平衡位置的偏离, 会导致原子体系势能的变化。在N个原子体系中, 如果将平衡位置设为参考点,即V0=0,势能函数在平衡位置附近可以展开成泰勒级数[30]:
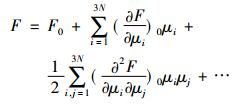
|
(5) |
由于一阶求导项为0。对于高阶项, 如果采用简谐近似(harmonic approximation), 公式(5)可以近似到二阶项[30]。对于包含N个原子核的材料, 热振动声子有3N个模式。但对于晶体来说, 由于晶格的平移对称性, 可以简化到用一个晶胞来描述。如果晶胞中含有r个原子核, 那么晶格振动模式的频率可以由对3r×3r动态矩阵(dynamic matrix)的对角化来求解[31]:
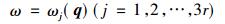
|
(6) |
频率ω与波矢q之间的关系称为色散关系。在该关系中, 包含3r个极化模式(又称分支, “branch”), 在公式(6)中由j标出。有3个分支的频率ω, 当q→0时(即长波极限)趋于零, 并在此极限下, 其频率与波矢有线性关系ω=υjq, 其中υj近似等于相应固体中的声速, 因此这3个分支被称为声学支(acoustic branches)。剩下的3r-3个分支, 在长波极限下有有限值, 并且相应的振动模式可以由电磁场(光)激发, 被称为光学支(optical branches)[31]。而每个分支根据相应的振动极化与振动传播的方向的关系, 又可以分为横波(transverse, 互相垂直)和纵波(longitudinal, 互相平行)[31]。
还有几点需要指出:①为了方便, 一般采用第一布里渊区来表述声子色散关系; ②声子是描述热振动的量子化准粒子, 属于玻色子, 满足玻色-爱因斯坦统计分布; ③根据色散关系, 可以得到声子模式在频率ω和ω+Δω之间的数目, 称为声子态密度(density-of-state, DOS)。
根据理想情况的简谐近似, 声子可以以平面波的形式在晶体中任意地传播, 其热导率将趋于无穷大。但实际上, 所有的材料的热导率总是有限的[31]。如果不考虑声子间的散射, 晶格热导率κlat可以准确描述为[32-33]
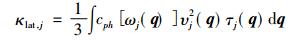
|
(7) |
其中cph为声子热容,υj为声子群速, τj为声子弛豫时间。如果忽略这些参数的频率依赖, 那么公式(7)可以简化为
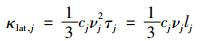
|
(8) |
其中lj=νjτj为声子平均自由程。
由此可见, 根据公式(1)和(4), 为了提高zT值, 需要减小晶格热导率。而根据公式(8), 可以通过减小声子群速或减小声子弛豫时间来减小晶格热导率。
声子群速度一般在键合相对松弛的材料中比较小。因此, 一种有效地减小声子群速的方法便是在材料晶体结构中引入所谓“松弛原子”(rattling atoms)[26]。中子散射实验证明这种松弛原子在材料中的振动可以有效地减小声子群速[7, 34-36]。
松弛原子在主要降低声子群速的同时, 也有影响了声子的弛豫时间。除此之外, 有更多因素可以被用来调节弛豫时间[10, 37], 比如非简谐振动(anharmonicity)引起的声子-声子相互作用[4, 38-40], 点缺陷对声子的散射[41-43], 以及微晶化后晶界对声子的散射[27, 44-48]等。这些因素对声子弛豫时间的叠加效应可以表达为[37]公式(9)等号右边各加和项分别代表一种声子散射机制的贡献。
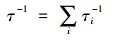
|
(9) |
除了上面提到的几种方法, 引入高原子质量比[49-52], 复杂的晶胞结构[12, 53-54], “离子液体晶体”[55-57]等都可以有效地降低晶格热导率, 提高热电zT优值。结合热电材料的功率因数α2σ以及热导率κ之间的相互关联, 优秀的热电材料需要一种特殊的“声子玻璃-电子晶体”材料[1, 10, 58]。因此在探寻热电材料的过程中, 研究与热导率相关的热振动和声子是一项非常重要的工作。而中子散射技术结合理论模拟是目前研究声子最强大的手段[59]。
2 中子散射技术中子由于其特殊的性质, 在物理、材料、化学以及生物等领域的研究上具有独特的地位[60]。首先, 中子具有静质量且不带电荷, 因此穿透深度比较大, 可以利用高压、高磁场, 极低温等极端条件; 其次, 中子带有1.913μN的磁矩, 在测定磁性材料的结构与动力学方面有着无法取代的地位; 再次, 中子与材料中原子核直接作用, 散射界面不依赖原子序数, 可以有效的区分近邻元素、同位素以及轻元素(如氢, 碳, 氧等), 是对电子、x射线散射技术的有效补充; 最后, 中子的德布罗意波长和动能大小与材料中原子间距及动力学处在同一量级, 在研究材料静态结构以及动力学信息方面有很重要的应用。
与其他粒子同材料的作用一样, 中子的散射截面也是非常重要的一个概念。根据费米黄金准则, 中子的微分散射截面定义为
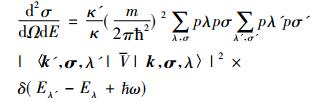
|
(10) |
k'和k是入射中子与出射中子波矢; σ'和σ是中子入射前初始状态|λ〉和出射后最终状态|λ'〉的极化; pλ和pσ分别为初始状态和入射中子的发生概率; 而入射(出射)中子的能量为Eλ和Eλ';是中子与样品之间作用的势能; δ为狄拉克德尔塔函数。对于中子与原子核之间的相互作用[61-62]:
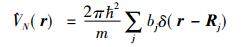
|
(11) |
其中r和Rj是中子和晶胞中第j个原子核的位矢,bj是第j个原子核的散射长度。根据公式(10), 可以定义出两个重要参数:
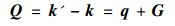
|
(12) |
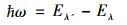
|
(13) |
Q和G称为散射矢量和倒格子矢量, q和ℏω分别为中子传递给样品的波矢量和能量。当ℏω=0时, 样品对中子的散射称为弹性散射, 即中子衍射; 当ℏω≠0时, 称为非弹性散射。
2.1 弹性中子散射技术中子相干弹性散射一般是指中子衍射。从公式(12)中很容易看出, 只有当Q=G(弹性散射时q=0)时才能得到衍射峰,因此Q=G是布拉格定律的另一种表达式。如果长程有序的晶体结构中出现热振动、缺陷引起的晶格畸变、静态偏离平衡位置、原子的无序占位等。
根据弹性中子衍射技术的特征[63], 在热电材料的研究中, 可以被用来确定材料的晶体结构、原子占位与分布、结构相变、结构畸变与内应力等。变温中子衍射实验可以给出晶胞参数随温度的变化趋势, 根据这个数据, 并应用格林内森常数(Grüneisen parameter, 公式(19))可以来判断非简谐热振动[64]:
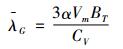
|
(14) |
其中α为线性热膨胀系数, Vm是摩尔体积, BT是等温体积模量, CV是等容比热。
2.2 非弹性中子散射技术不同于弹性中子散射模式, 对于非弹性中子散射, 由于在散射过程中伴随着中子与散射物质之间的能量传递, 其微分散射截面不能忽略对能量的微分[63, 65]。如果只考虑单声子的产生和湮灭引起的相干散射, 那么非弹性中子散射测出的单声子色散关系谱应该是连续的细峰。已在1.2小节中指出, 由于很多不同因素对声子的散射, 导致声子谱偏离理想的简谐模式。如果这种偏离比较小, 那么依然可以用声子色散关系来描述, 但是相应的声子谱能量峰值会发生偏移, 而且弛豫时间(或寿命)减小会导致声子谱半高宽(full width at half maximum, FWHM, 又称线宽linewidth, Γ(qj, Ω)), 与声子弛豫时间(寿命)τ之间的关系为
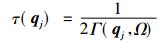
|
(15) |
单晶的非弹性散射测试可以直接给出动量空间中的声子谱, 并给出声子谱的偏移与峰宽, 从而提供非简谐热振动的详细信息。如果是多晶样品的话, 则可以得到声子的态密度(DOS), 从而得到材料热动力学的重要信息[66]。
2.3 中子散射谱仪简介类似于x射线衍射仪, 中子散射谱仪也由中子源(source)、单色器(monochromator)、样品台(sample stage)、探测器(detector)和光路系统(Goniometers)组成。现在通用的中子源有两种, 一种是反应堆(reactor), 另一种是散裂中子源(spallation neutron source)。根据不同的中子源, 可以选择搭建不同的谱仪, 例如三轴谱仪(triple-axis spectrometer, TAS)和时间飞行谱仪(time-of-flight spectrometer, TOF)。在材料微观动力学的研究中, 包括声子、磁子(magnon)、自旋子(spinon)等[67]。
3 中子散射技术在热电材料中的应用 3.1 PbTe-强非简谐作用具有氯化钠结构的PbTe具有非常低的晶格热导率[68], 是典型的热电材料。通过弹性与非弹性中子散射实验, 可以更好地理解这种物质的低晶格热导率[69-72]。
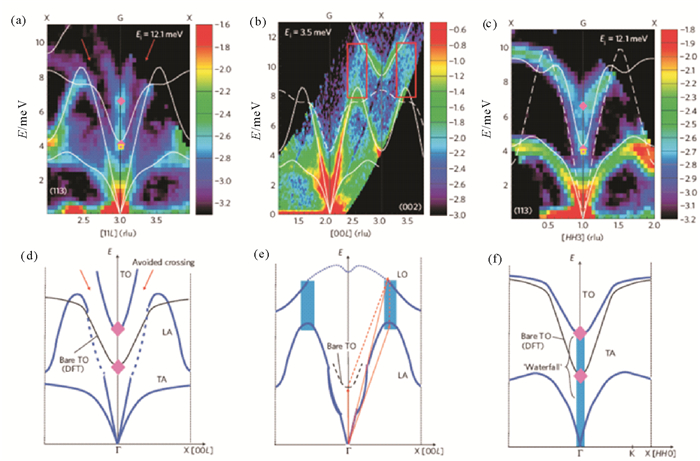
图 2(a)-(c)是PbTe在300K下, 分别是在布里渊区(113),(002),(113)沿着[110],[001]方向测得的声子色散关系[69]。图 2中最明显的一个特征就是纵声学支(longitudinal acoustic, LA)和横光学支(transverse optical, TO)之间的相互作用(见图 2(a)), 区别与DFT计算的简谐色散关系。伴随着LA和TO之间在q=2.8和3.2处的相互排斥。
|
图中的实线和虚线是通过DFT计算的简谐色散关系。(d)-(f)是色散关系的示意图[69]。 图 2 (a)-(c)PbTe声子色散关系 Fig. 2 Anomalous feastures of phonon dispersions in PbTe at 300 K |
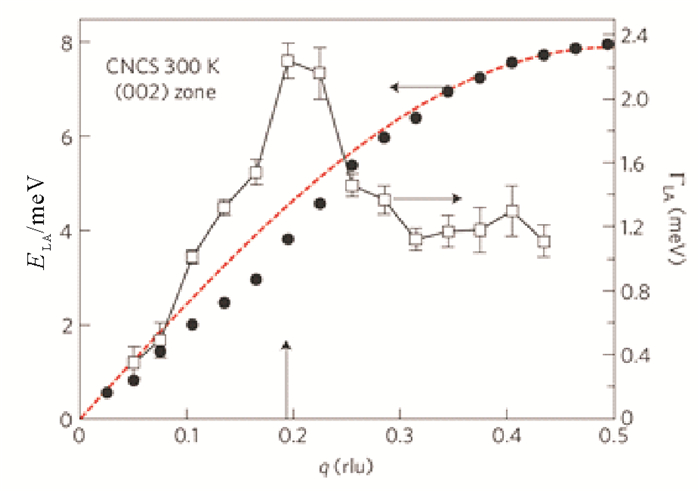
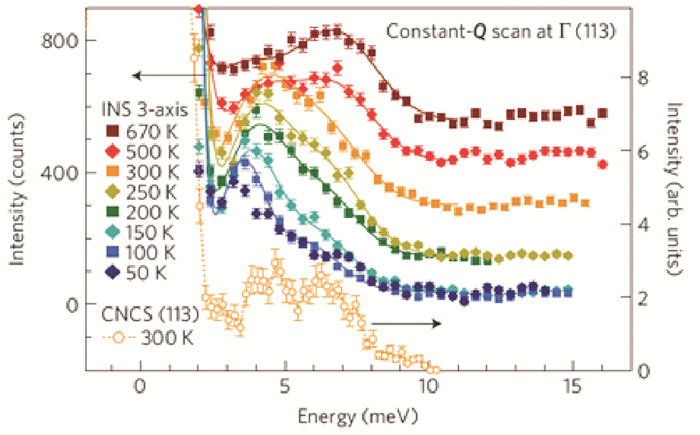
由于(113)区域中的声子过于密集。我们利用中子散射技术对声子测量的优势, 对横波和纵波分别讨论。比如(002)区域中(图 2(b)), 沿[001]方向主要对LA与LO进行研究。首先, 由于三声子相互作用, LA和LO之间观察到了额外的散射谱(q=0.5, 由图 2(b)和(e)中的红色方框和蓝色方块标出)。通过对图 2(b)中色散谱的LA进行详细的恒Q切片(constant-Q cut)分析发现(见图 3), LA色散关系在(002)区域q为0.2处存在一个异常, 并且同时观察到其色散谱的线宽明显变宽。这些异常特征说明TO和LA之间存着非简谐交互作用, 并导致了LA的软化与弱化。如图 2(c)所示, 在(113)区域沿[110]方向主要对TA与TO进行研究:TO在中心区域出现异常:当q接近于Γ点时, 能量由E≈6.5meV突然掉到~4.0meV, 在能量上形成一个“瀑布”(waterfall)效应。三轴谱仪测试结果(见图 4)也指出, TO随着温度的升高, 逐渐向高能量方向移动。在高温区域非弹性中子散射峰型变得很复杂:TO明显的变成了双峰; 随着温度升高其中低能量峰变得越来越弱, 高能峰逐渐变强。
|
图 3 PbTe在(002)区域沿着[001]方向LA声子色散谱(ELA)以及其线宽(ΓLA)的异常特征[69] Fig. 3 Anomaly of LA-mode phonon dispersion (ELA) and linewidth (ΓLA) at q~0.2 along [00L] |
|
图 4 PbTe的TO声学支的在布里渊区中心Γ=(113)处的能量峰型随温度的变化[69] Fig. 4 Temperature dependence of the TO-mode profile in energy at the zone center Γ=(113) |
从上面的讨论可知, PbTe中声子谱的非简谐性是由TO和LA之间的耦合引起[69]。结合理论计算, PbTe作为一种优良热电材料的起源是材料中很强的声子间相互作用, 并且这一相互作用与TO的双峰起源密切相关[70-71]。目前, 认为PbTe中TO的双峰起源于其铁电性质[73]:由于Pb 6p-Te 5p轨道的杂化, 其被广泛认为是赝铁电材料(铁电转变温度为负值)[74]。但是Pb半充满的p轨道以及Te的非线性极化导致铁电失稳, 从而引起非简谐的离子势能[75]。这种非简谐离子势能将会导致TO声子在布里渊区中心畸变, 从而偏离赝简谐模型[66]。因此, 铁电性能材料应该是热电材料的一个明确的研究方向。
3.2 SnTe—强嵌套效应根据铁电性能对热电性能显著影响的思路, 我们研究了PbTe的同构材料SnTe(SnTe的铁电转变温度是42K)。如果铁电效应是PbTe中光学支与声学支相互作用的起源, SnTe中同样也应该存在宽化的TO声子双峰。然而在SnTe中, 由于载流子的浓度很高, 在Γ点并没有出现了TO声子色散谱的双峰(LO声子与TO声子没有像PbTe那样很好的分离), 而是仅仅出现了一段很宽化的信号, 如图 5所示。

|
(a),(b)是SnTe在T=50和300 K下测得的声子谱。(d),(e)是相对应的PbTe的声子谱。图中白线是用简谐振动模式计算的声子谱。(c),(f)是利用声子自能修正计算的相应动量空间的声子谱[70]。 图 5 PbTe和SnTe的声子谱与理论计算的比较 Fig. 5 Phonon dispersions in PbTe and SnTe measured with inelastic neutron scattering compared with first-principle anharmonic lattice dynamics |
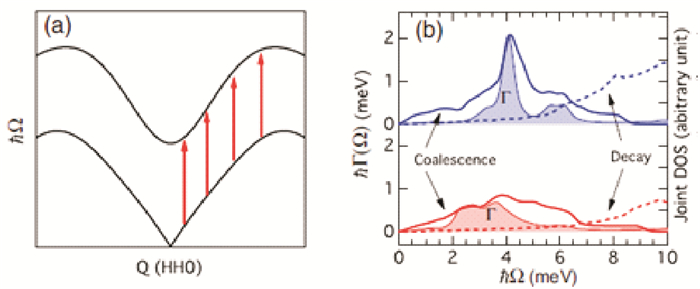
因此, 表面上看, 如果简单地将非简谐声子模型与TO声子的双峰分离直接联系起来, 更具有铁电结构不稳定性的SnTe反而比赝铁电材料PbTe中的声子相互作用更弱。为了解释这一悖论, 我们需要进一步分析体系内能的高阶项, 即引入自能修正。如图 6(b)所示, SnTe与PbTe自能修正的虚部对比表明, PbTe的相关态密度更尖锐; 同时, 相比SnTe, PbTe中存在着更强的声子谱嵌套(nesting), 因此相比于SnTe中的单一长尾巴, PbTe中的TO演化为双峰[66]。这一结果在明确指出了两种材料均存在很强的非简谐效应的同时, 表明了声子谱的奇异现象是多种因素共同作用的结果[70]。
|
图 6 (a) 声学支与光学支嵌套示意图; (b)声子自能的虚部与相关态密度的对比[70] Fig. 6 (a) Schematic of nestingbetween acoustic and optical phonon branches; (b) Imaginary part of the phonon self-energy, Γ (shadedarea), and joint density of states (lines) |
AgSbTe2同样具有较低热导率的氯化钠结构化合物, κ≈0.7Wm-1K-1, 也是另一种优异的热电材料[76-77]。同时, 其热导率的温度依赖性很低, 具有很大的应用前景。因此, 对于其特殊热导率驱动力的研究一直是科研和工业界的热点。目前已经提出的解释包括强的非简谐性、应力常数的各向异性、杂质纳米晶粒析出、晶格热导率已经达到了相应原子间距的理论极限等等[78-79]。通过中子衍射、非弹性中子散射实验以及电镜测试, 我们发现了AgSbTe2具有低热导的根本原因是材料中一种自发生成的纳米团簇[80]。
Ag-Sb-Te系列材料的化学成分配比可以表达为
(Ag2Te)(1-x)/2(Sb2Te3)(1+x)/2=Ag1-xSb1+xTe2+x。在x=0时, 可以得到AgSbTe2, 且含有少量的Ag2Te杂相; x=0.1中, 同样含有少量的Ag2Te杂相; x=0.2时, 样品处于δ-相, 没有杂相。3个样品主要由氯化钠结构的δ-相构成[80]。
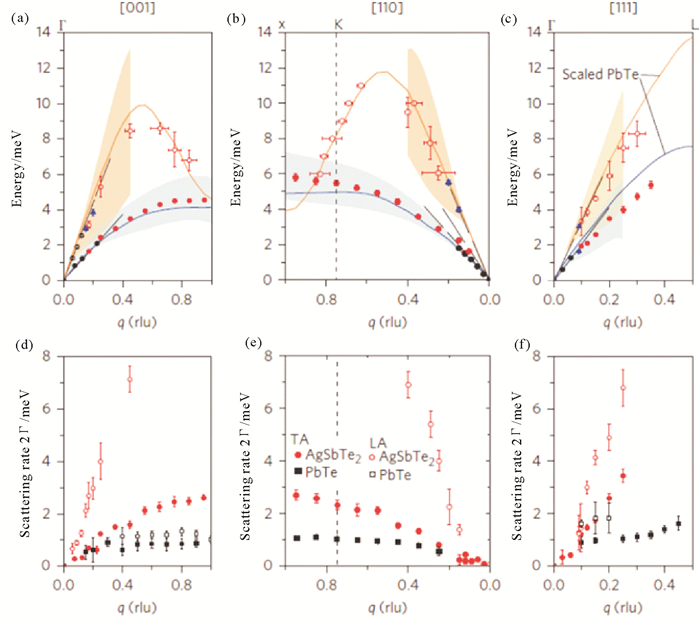
图 7是AgSbTe2的色散关系谱以及相应的线宽。从图 7中可以看出, 纵声学支LA和横声学支TA在低能区域都很清晰, 但是在高能区域, LA和光学支变得很宽, 以致于无法区分。因此样品中的晶格热导率主要来自于横波声学支的贡献。通过与PbTe声子峰宽及约化声子色散谱对比, 如图 7所示, 两种样品中的平均应力常数基本一致, 因而排除了用局域应力常数来解释AgSbTe2中极低热导率可能性。
|
(a)-(c)声子色散谱; (d)-(f)声子线宽2Γ。(a)-(c)平滑曲线是约化的PbTe声子谱[80]。直虚线是由共振超声波测得。 图 7 AgSbTe2在300K的声子谱图 Fig. 7 Single-crystal phonon spectraof AgSbTe2 at 300 K |
图 8(a)是Ag1-xSb1+xTe2+x (x=0, 0.2)粉末样品在40 K时的声子态密度DOS。一个样品含有Ag2Sb杂相而另一个没有, 在误差范围之内两个样品的DOS谱没有差别。因此, Ag2Sb杂相对材料的热导率没有影响。结合声子平均能量〈E〉随温度的变化以及对比实验与简谐模型获得的〈u2〉iso的对比, 图 8(b)和(c), 我们进一步发现该声子的软化行更符合仅与体积相关的赝简谐模型(QH)而不是与体积、温度均相关的非简谐模型。同时我们发现:除了QH贡献外, 还有一部分额外的未知贡献, 而且这部分贡献比较稳定, 与温度依赖关系很小。这个结果指出,非简谐声子散射在300K以下对晶格热导率的贡献很有限。另外, 如图 8(d)~(f)所示, 声子相互作用和点缺陷散射的对TA的线宽2Γ贡献有限。

|
图 8 (a) Ag1-xSb1+xTe2+x (x=0, 0.2)粉末样品在40 K时的声子态密度DOS。(b)平均声子能量〈E(T)〉/〈E(T)〉40K随温度的变化。(c)由中子粉末衍射测得的以及根据声子DOS算得的均方位移〈u2〉。(d)-(f)q=0.175Å-1处TA的线宽, 对比于计算获得的声子相互作用和点缺陷散射的贡献[80]。 Fig. 8 Limited anharmonicity in Ag1-xSb1+xTe2+x below 300 K and Linewidth of TA, compared with the contribution from umklapp scattering and point-defect scattering |
根据之前对AgSbTe2声子谱的测量(图 7)我们可以得到声子的群速度与弛豫时间, 从而可以计算出相应声子的平均自由程(1.2节)。我们发现AgSbTe2体系中的平均自由程远大于相应的原子间距。因此, 该材料远未达到之前提出的晶格热导理论极限。
综合上述实验结果, 强的非简谐性、局域应力常数、杂质纳米晶粒析出以及晶格距离极限都不可能是AgSbTe2中晶格热导率极低的原因。而且通过计算比较得出, 样品中的点缺陷也不是主要原因。因此, 之前提出的AgSbTe2有关低热导源驱动力的解释均是值得商榷的。
为研究AgSbTe2的与温度不相关的低热导率, 我们以赝简谐与简谐模型在低温具有固定差值为出发点, 利用透射电镜和弹性中子漫散射技术测试了样品, 发现AgSbTe2中的Ag离子和Sb离子并不是随机占据在氯化钠结构的钠离子位置, 而是存在着一定的有序性。同时, 这一有序性的占据诱发该种材料中存在复杂的纳米结构, 从而导致了极低的晶格热导率[80-81]。
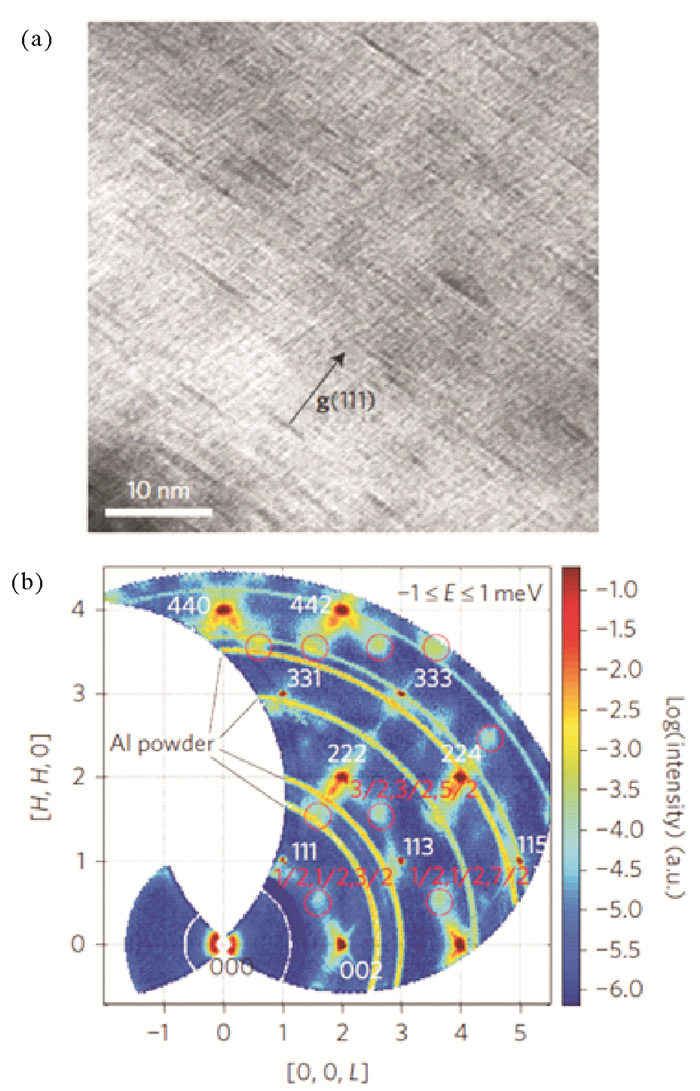
如图 9(a)所示, TEM谱图显示了AgSbTe2δ-相的纳米团簇, 并且该团簇有一定的方向性, 即[111]方向; 图 9(b)显示了弹性中子散射在测得布拉格衍射峰周围的蝴蝶状漫散射峰的同时, 还在1/2(hkl) (其中h, k, l为奇数)位置观察到了一些多余的衍射峰, 但这些衍射峰并不属于δ-相的氯化钠结构。通过分析不同温度下这些额外的衍射峰变化, 确定这些衍射峰是材料中的结构峰, 而不是与动力学相关的热漫散射[81]。这一发现与理论分析的结果相一致:在AgSbTe2中沿[111]方向存在着Ag和Sb原子的超晶格排序, 从而形成具有R-3m结构L11相[82-84]。而图 9(b)中观察到的超晶格衍射峰正好和L11相相符合, 从而印证了AgSbTe2中自发的微晶化可能正是由超晶格的出现而引起, 从而导致了其极低的晶格热导率[80-81]。
|
图 9 (a) AgSbTe2δ-相中(111)方向透射电镜双束亮场衍射对比图。(b)弹性中子漫散射图。红色圆圈标记出1/2(hkl)超晶格衍射点, 其中h, k, l为奇数[80] Fig. 9 Nanostructure in δ-phase AgSbTe2 studied by TEM and neutron diffuse scattering |
热电材料作为一种无污染的能源转换材料, 可以在全球能源危机和环境恶化等情况中发挥重要的作用。各种热电参数之间的相互耦合增加了提高热电材料性能困难, 也为热电材料的发展提供了机遇。除了裁剪能带结构外, 降低材料的晶格热导率被广泛地认为是一种有效的提高热电优值方法, 其核心思路是减小声子的群速度和寿命。而了解其具体的微观机制对提高现有材料的性能、设计新材料以及开发应用具有指导性的意义。本文以热电材料的物理机制为出发点, 结合优化热电性能的具体方法, 通过实际应用事例, 阐述了中子散射技术在热电材料方面的重要应用:弹性中子衍射与漫散射技术, 可以帮助获得材料的晶体结构, 解析晶体中的原子占位与分布、均方位移、晶格常数、局域应变、原子紊乱程度等; 非弹性中子散射技术可以被用来测绘动量空间内的声子色散关系谱和态密度。通过不同温度、压力、掺杂等情况下的对比, 结合理论计算与模拟, 可以揭示材料中晶格热导率主导因素。
近些年来, 国内在热电材料本身的研发上一直处在世界前列。随着北京中国先进研究堆(CARR)[60]、四川中国绵阳研究堆(CMRR)及东莞中国散裂中子源(CSNS)的建成和使用, 国内科研人员可以获得了测量声子谱的直接测量技术, 国内在热电材料领域的研究将得到进一步的发展[85-86]。
| [1] |
SOOTSMAN J R, CHUNG D Y, KANATZIDIS M G. New and old concepts in thermoelectric materials[J]. Angewandte Chemie, International Edition in English, 2009, 48(46): 8616-39. DOI:10.1002/anie.v48:46 |
| [2] |
GUTFLEISCH O, WILLARD M A, BRUCK E, et al. Magnetic materials and devices for the 21st century: stronger, lighter, and more energy efficient[J]. Advanced Materials, 2011, 23(7): 821-842. DOI:10.1002/adma.v23.7 |
| [3] |
MINNICH A J, DRESSELHAUS M S, REN Z F, et al. Bulk nanostructured thermoelectric materials: current research and future prospects[J]. Energy & Environmental Science, 2009, 2(5): 466. |
| [4] |
ZHANG X, ZHAO L-D. Thermoelectric materials: Energy[J]. Materiomics, 2015, 1(2): 92-105. DOI:10.1016/j.jmat.2015.01.001 |
| [5] |
DRESSELHAUS M S, CHEN G, TANG M Y, et al. New directions for low-dimensional thermoelectric materials[J]. Advanced Materials, 2007, 19(8): 1043-1053. DOI:10.1002/adma.v19:8 |
| [6] |
BELL L E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems[J]. Science, 2008, 321(5895): 1457-1461. DOI:10.1126/science.1158899 |
| [7] |
CHRISTENSEN M, ABRAHAMSEN A B, CHRISTENSEN N B, et al. Avoided crossing of rattler modes in thermoelectric materials[J]. Nature Materials, 2008, 7(10): 811-5. DOI:10.1038/nmat2273 |
| [8] |
GOLDSMID H J. Introduction to thermoelectricity [M]. Springer, 2010.
|
| [9] |
LALONDE A D, PEI Y, WANG H, et al. Lead telluride alloy thermoelectrics[J]. Materials Today, 2011, 14(11): 526-532. DOI:10.1016/S1369-7021(11)70278-4 |
| [10] |
SNYDER G J, TOBERER E S. Complex thermoelectric materials[J]. Nature Materials, 2008, 7(2): 105-114. DOI:10.1038/nmat2090 |
| [11] |
SALES B C, MANDRUS D, WILLIAMS R K. Filled skutterudite antimonides: A new class of thermoelectric materials[J]. Science, 1996, 272(5266): 1325-1328. DOI:10.1126/science.272.5266.1325 |
| [12] |
COX C A, TOBERER E S, LEVCHENKO A A, et al. Structure, heat capacity, and high-temperature thermal properties of Yb14Mn1-xAlxSb11[J]. Chemistry of Materials, 2009, 21(7): 1354-1360. DOI:10.1021/cm803252r |
| [13] |
ROWE D M, MIN G. α-in σ plot as a thermoelectric material performance indicator[J]. Journal of Materials Science Letters, 1995, 14(9): 617-619. DOI:10.1007/BF00586157 |
| [14] |
PEI Y, WANG H, SNYDER G J. Band engineering of thermoelectric materials[J]. Advanced Materials, 2012, 24(46): 6125-35. DOI:10.1002/adma.v24.46 |
| [15] |
ZHAO L D, WU H J, HAO S Q, et al. All-scale hierarchical thermoelectrics: MgTe in PbTe facilitates valence band convergence and suppresses bipolar thermal transport for high performance[J]. Energy & Environmental Science, 2013, 6(11): 3346. |
| [16] |
ENERGY ENVIRON, SCI.HEREMANS J P, WIENDLOCHA B, CHAMOIRE A M. Resonant levels in bulk thermoelectric semiconductors[J]. Energy & Environmental Science, 2012, 5(2): 5510-5530. |
| [17] |
WANG H, GIBBS Z M, TAKAGIWA Y, et al. Tuning bands of PbSe for better thermoelectric efficiency[J]. Energy & Environmental Science, 2014, 7(2): 804-811. |
| [18] |
TAN G, ZHAO L D, SHI F, et al. High thermoelectric performance of p-type SnTe via a synergistic band engineering and nanostructuring approach[J]. Journal of the American Chemical Society, 2014, 136(19): 7006-17. DOI:10.1021/ja500860m |
| [19] |
PEI Y, SHI X, LALONDE A, et al. Convergence of electronic bands for high performance bulk thermoelectrics[J]. Nature, 2011, 473(7345): 66-9. DOI:10.1038/nature09996 |
| [20] |
PEI Y, WANG H, GIBBS Z M, et al. Thermopower enhancement in Pb1-xMnxTe alloys and its effect on thermoelectric efficiency[J]. NPG Asia Materials, 2012, 4(9): e28. DOI:10.1038/am.2012.52 |
| [21] |
LIU W, TAN X, YIN K, et al. Convergence of conduction bands as a means of enhancing thermoelectric performance of n-type Mg2Si1-xSnx solid solutions[J]. Physical Review Letters, 2012, 108(16): 166601. DOI:10.1103/PhysRevLett.108.166601 |
| [22] |
MAY A F, SINGH D J, SNYDER G J. Influence of band structure on the large thermoelectric performance of lanthanum telluride[J]. Physical Review B, 2009, 79(15): 153101. DOI:10.1103/PhysRevB.79.153101 |
| [23] |
WANG H, CHAROENPHAKDEE A, KUROSAKI K, et al. Reduction of thermal conductivity in PbTe:Tl by alloying with TlSbTe2[J]. Physical Review B, 2011, 83(2): 024303. DOI:10.1103/PhysRevB.83.024303 |
| [24] |
HEREMANS J P, JOVOVIC V, TOBERER E S, et al. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states[J]. Science, 2008, 321(5888): 554-557. DOI:10.1126/science.1159725 |
| [25] |
ZHAO L-D, TAN G, HAO S, et al. Ultrahigh power factor and thermoelectric performance in hole-doped single-crystal SnSe[J]. Science, 2015, aad3749. |
| [26] |
TOBERER E S, MAY A F, SNYDER G J. Zintl chemistry for designing high efficiency thermoelectric materials[J]. Chemistry of Materials, 2010, 22(3): 624-634. DOI:10.1021/cm901956r |
| [27] |
ZHANG Q, LIAO B, LAN Y, et al. High thermoelectric performance by resonant dopant indium in nanostructured SnTe[J]. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(33): 13261-13266. DOI:10.1073/pnas.1305735110 |
| [28] |
VASHAEE D, SHAKOURI A. Improved thermoelectric power factor in metal-based superlattices[J]. Physical Review Letters, 2004, 92(10): 106103. DOI:10.1103/PhysRevLett.92.106103 |
| [29] |
ZIDE J M O, VASHAEE D, BIAN Z X, et al. Demonstration of electron filtering to increase the Seebeck coefficient inIn0.53Ga0.47As/In0.53Ga0.28Al0.19Assuperlattices[J]. Physical Review B, 2006, 74(20): 205335. DOI:10.1103/PhysRevB.74.205335 |
| [30] |
黄昆, 韩汝琦. 固体物理学[M]. 北京: 人民教育出版社, 1979.
|
| [31] |
DELAIRE O A, STASSIS C. Phonon Studies, in Characterization of Materials [M].John Wiley & Sons, Inc., 2012.
|
| [32] |
TRITT T M. Thermal Conductivity: Theory, Properties, and Applications[M]. New York: Springer Science & Business Media, 2005.
|
| [33] |
WARD A, BROIDO D A. Intrinsic phonon relaxation times from first-principles studies of the thermal conductivities of Si and Ge[J]. Physical Review B, 2010, 81(8): 085205. DOI:10.1103/PhysRevB.81.085205 |
| [34] |
KEPPENS V, MANDRUS D, SALES B C, et al. Localized vibrational modes in metallic solids[J]. Nature, 1998, 395(6705): 876-878. DOI:10.1038/27625 |
| [35] |
CHRISTENSEN M, LOCK N, OVERGAARD J, et al. Crystal structures of thermoelectric n-and p-type Ba8Ga16Ge30 studied by single crystal, multitemperature, neutron diffraction, conventional X-ray diffraction and resonant synchrotron X-ray diffraction[J]. Journal of the American Chemical Society, 2006, 128(49): 15657-15665. DOI:10.1021/ja063695y |
| [36] |
KOZA M M, JOHNSON M R, VIENNOIS R, et al. Breakdown of phonon glass paradigm in La-and Ce-filled Fe4Sb12 skutterudites[J]. Nature Materials, 2008, 7(10): 805-10. DOI:10.1038/nmat2260 |
| [37] |
TOBERER E S, ZEVALKINK A, SNYDER G J. Phonon engineering through crystal chemistry[J]. Journal of Materials Chemistry, 2011, 21(40): 15843. DOI:10.1039/c1jm11754h |
| [38] |
BOŽIN E S, MALLIAKAS C D, SOUVATZIS P, et al. Entropically Stabilized Local Dipole Formation in Lead Chalcogenides[J]. Science, 2010, 330(6011): 1660-1663. DOI:10.1126/science.1192759 |
| [39] |
WANG H, PEI Y, LALONDE A D, et al. Heavily doped p-type PbSe with high thermoelectric performance: An alternative for PbTe[J]. Advanced Materials, 2011, 23(11): 1366-70. DOI:10.1002/adma.v23.11 |
| [40] |
ZHAO L D, LO S H, ZHANG Y, et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals[J]. Nature, 2014, 508(7496): 373-7. DOI:10.1038/nature13184 |
| [41] |
PEI Y L, HE J, LI J F, et al. High thermoelectric performance of oxyselenides: Intrinsically low thermal conductivity of Ca-doped BiCuSeO[J]. NPG Asia Materials, 2013, 5(5): e47. DOI:10.1038/am.2013.15 |
| [42] |
HU L, ZHU T, LIU X, et al. Point defect engineering of high-performance bismuth-telluride-based thermoelectric materials[J]. Advanced Functional Materials, 2014, 24(33): 5211-5218. DOI:10.1002/adfm.v24.33 |
| [43] |
JIANG G, HE J, ZHU T, et al. High performance Mg2(Si, Sn) solid solutions: A point defect chemistry approach to enhancing thermoelectric properties[J]. Advanced Functional Materials, 2014, 24(24): 3776-3781. DOI:10.1002/adfm.v24.24 |
| [44] |
KANATZIDIS M G. Nanostructured thermoelectrics: The new paradigm?[J]. Chemistry of Materials, 2010, 22(3): 648-659. DOI:10.1021/cm902195j |
| [45] |
LAN Y, MINNICH A J, CHEN G, et al. Enhancement of thermoelectric figure-of-merit by a bulk nanostructuring approach[J]. Advanced Functional Materials, 2010, 20(3): 357-376. DOI:10.1002/adfm.v20:3 |
| [46] |
VINEIS C J, SHAKOURI A, MAJUMDAR A, et al. Nanostructured thermoelectrics: Big efficiency gains from small features[J]. Advanced Materials, 2010, 22(36): 3970-80. DOI:10.1002/adma.201000839 |
| [47] |
NIELSCH K, BACHMANN J, KIMLING J, et al. Thermoelectric nanostructures: From physical model systems towards nanograined composites[J]. Advanced Energy Materials, 2011, 1(5): 713-731. DOI:10.1002/aenm.v1.5 |
| [48] |
ZEBARJADI M, ESFARJANI K, DRESSELHAUS M S, et al. Perspectives on thermoelectrics: from fundamentals to device applications[J]. Energy & Environmental Science, 2012, 5(1): 5147-5162. |
| [49] |
CUI Y, YI C, HANHUI X, et al. Improved thermoelectric properties in Lu-doped Yb14MnSb11 Zintl compounds[J]. Applied Physics Express, 2012, 5(3): 031801. DOI:10.1143/APEX.5.031801 |
| [50] |
MÖCHEL A, SERGUEEV I, WILLE H C, et al. Lattice dynamics in the thermoelectric Zintl compound Yb14MnSb11[J]. Physical Review B, 2011, 84(18): 184303. DOI:10.1103/PhysRevB.84.184303 |
| [51] |
COX C A, BROWN S R, SNYDER G J, et al. Effect of Ca doping on the thermoelectric performance of Yb14MnSb11[J]. Journal of Electronic Materials, 2010, 39(9): 1373-1375. DOI:10.1007/s11664-010-1149-9 |
| [52] |
BROWN S R, KAUZLARICH S M, GASCOIN F, et al. Yb14MnSb11:? New high efficiency thermoelectric material for power generation[J]. Chemistry of Materials, 2006, 18(7): 1873-1877. DOI:10.1021/cm060261t |
| [53] |
PADTURE N P, KLEMENS P G. Low thermal conductivity in garnets[J]. Journal of the American Ceramic Society, 1997, 80(4): 1018-1020. |
| [54] |
WINTER M R, CLARKE D R. Oxide materials with low thermal conductivity[J]. Journal of the American Ceramic Society, 2007, 90(2): 533-540. DOI:10.1111/jace.2007.90.issue-2 |
| [55] |
LIU H, SHI X, XU F, et al. Copper ion liquid-like thermoelectrics[J]. Nature Materials, 2012, 11(5): 422-5. DOI:10.1038/nmat3273 |
| [56] |
HE Y, DAY T, ZHANG T, et al. High thermoelectric performance in nontoxic earth-abundant copper sulfide[J]. Advanced Materials, 2014, 26(23): 3974-8. DOI:10.1002/adma.201400515 |
| [57] |
SNYDER G J, CHRISTENSEN M, NISHIBORI E, et al. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties[J]. Nature Materials, 2004, 3(7): 458-63. DOI:10.1038/nmat1154 |
| [58] |
ROWE D M. CRC handbook of thermoelectrics[M]. CRC Press, 1995.
|
| [59] |
NOLAS G S, SHARP J, GOLDSMID J. Thermoelectrics: Basic principles and new materials developments[M]. Springer Science & Business Media, 2013.
|
| [60] |
李世亮戴. 中子三轴谱仪的原理、技术与应用[J]. 物理, 2011, 40(01): 33-39. |
| [61] |
CHATTERJI T. Neutron Scattering from Magnetic Materials[M]. Amsterdam: Elsevier, 2006.
|
| [62] |
FURRER A, MESOT J, STRÄSSLE T. Neutron Scattering in Condensed Matter Physics[M]. Singapore: World Scientific, 2009.
|
| [63] |
SQUIRES G L. Introduction to the Theory of Thermal Neutron Scattering[M]. Cambridge: Cambridge University Press, 2012.
|
| [64] |
GRIMVALL G. Thermophysical Properties of Materials[M]. Elsevier, 1999.
|
| [65] |
LOVESEY S W. Theory of Neutron Scattering from Condensed Matter[M]. Oxford: Clarendon Press, 1984.
|
| [66] |
FULTZ B. Vibrational thermodynamics of materials[J]. Progress in Materials Science, 2010, 55(4): 247-352. DOI:10.1016/j.pmatsci.2009.05.002 |
| [67] |
SHIRANE G, SHAPIRO S M, TRANQUADA J M. Neutron Scattering with a Triple-Axis Spectrometer: Basic Techniques[M]. Cambridge: Cambridge University Press, 2002.
|
| [68] |
AKHMEDOVA G A, ABDINOV D S. Effect of thallium doping on the thermal conductivity of PbTe single crystals[J]. Inorganic Materials, 2009, 45(8): 854-858. DOI:10.1134/S0020168509080056 |
| [69] |
DELAIRE O, MA J, MARTY K, et al. Giant anharmonic phonon scattering in PbTe[J]. Nature Materials, 2011, 10(8): 614-9. DOI:10.1038/nmat3035 |
| [70] |
LI C W, HELLMAN O, MA J, et al. Phonon self-energy and origin of anomalous neutron scattering spectra in SnTe and PbTe thermoelectrics[J]. Physical Review Letters, 2014, 112(17): 175-501. |
| [71] |
LI C W, MA J, CAO H B, et al. Anharmonicity and atomic distribution of SnTe and PbTe thermoelectrics[J]. Physical Review B, 2014, 90(21): 214-303. |
| [72] |
SHIGA T, SHIOMI J, MA J, et al. Microscopic mechanism of low thermal conductivity in lead telluride[J]. Physical Review B, 2012, 85(15): 155-203. |
| [73] |
BATE R T, CARTER D L, WROBEL J S. Paraelectric Behavior of PbTe[J]. Physical Review Letters, 1970, 25(3): 159-162. DOI:10.1103/PhysRevLett.25.159 |
| [74] |
WAGHMARE U V, SPALDIN N A, KANDPAL H C, et al. First-principles indicators of metallicity and cation off-centricity in the Ⅳ-Ⅵ rocksalt chalcogenides of divalent Ge, Sn, and Pb[J]. Physical Review B, 2003, 67(12): 125111. DOI:10.1103/PhysRevB.67.125111 |
| [75] |
ZHANG Y, KE X, KENT P R, et al. Anomalous lattice dynamics near the ferroelectric instability in PbTe[J]. Physical Review Letters, 2011, 107(17): 175503. DOI:10.1103/PhysRevLett.107.175503 |
| [76] |
GUIN S N, CHATTERJEE A, NEGI D S, et al. High thermoelectric performance in tellurium free p-type AgSbSe2[J]. Energy & Environmental Science, 2013, 6(9): 2603. |
| [77] |
NIELSEN M D, OZOLINS V, HEREMANS J P. Lone pair electrons minimize lattice thermal conductivity[J]. Energy & Environmental Science, 2013, 6(2): 570-578. |
| [78] |
JOVOVIC V, HEREMANS J P. Measurements of the energy band gap and valence band structure ofAgSbTe2[J]. Physical Review B, 2008, 77(24): 245204. DOI:10.1103/PhysRevB.77.245204 |
| [79] |
MORELLI D T, JOVOVIC V, HEREMANS J P. Intrinsically minimal thermal conductivity in cubic Ⅰ-Ⅴ-Ⅵ2 semiconductors[J]. Physical Review Letters, 2008, 101(3): 035901. DOI:10.1103/PhysRevLett.101.035901 |
| [80] |
MA J, DELAIRE O, MAY A F, et al. Glass-like phonon scattering from a spontaneous nanostructure in AgSbTe2[J]. Nature Nanotechnology, 2013, 8(6): 445. DOI:10.1038/nnano.2013.95 |
| [81] |
MA J, DELAIRE O, SPECHT E D, et al. Phonon scattering rates and atomic ordering in Ag1-xSb1+xTe2+x (x=0, 0.1, 0.2)investigated with inelastic neutron scattering and synchrotron diffraction[J]. Physical Review B, 2014, 90(13): 134303. DOI:10.1103/PhysRevB.90.134303 |
| [82] |
BARABASH S V, OZOLINS V. Order, miscibility, and electronic structure of Ag(Bi, Sb)Te2 alloys and (Ag, Bi, Sb)Te precipitates in rocksalt matrix: A first-principles study[J]. Physical Review B, 2010, 81(7). |
| [83] |
BARABASH S V, OZOLINS V, WOLVERTON C. First-principles theory of competing order types, phase separation, and phonon spectra in thermoelectric AgPbmSbTem+2alloys[J]. Physical Review Letters, 2008, 101(15): 155704. DOI:10.1103/PhysRevLett.101.155704 |
| [84] |
HOANG K, MAHANTI S D, SALVADOR J R, et al. Atomic ordering and gap formation in Ag-Sb-based ternary chalcogenides[J]. Physical Review Letters, 2007, 99(15): 156403. DOI:10.1103/PhysRevLett.99.156403 |
| [85] |
WEI J, CHEN H, CHEN Y, et al. China spallation neutron source: Design, R & D, and outlook[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2009, 600(1): 10-13. |
| [86] |
WEI J, FU S N, TANG J Y, et al. China Spallation Neutron Source-an overview of application prospects[J]. Chinese Physics C, 2009, 33(11): 1033. DOI:10.1088/1674-1137/33/11/021 |
 2017, Vol. 47
2017, Vol. 47