冯诺依曼代数理论是现代数学中一个非常活跃的研究领域。它是由约翰·冯诺依曼在1929年首次提出。其后, 冯诺依曼与其合作者Francis Murray在1930—1940年代对该理论展开了系统研究, 从而奠定了该学科的理论基础。在其第一篇论文《关于算子环》^[1]中, Murray和冯诺依曼特别提到发展该学科的目的是“试图推广酉群表示理论”且“满足量子力学数学化的各个方面需求”。

作为纯数学理论分支, 无论在思想上还是在技巧上, 冯诺依曼代数都已经发展到一个高深而丰富的层次, 并且与诸如群论、表示论、动力系统、遍历理论、量子物理、纽结理论、概率论、随机矩阵论等众学科建立起密切多样的联系。在该领域的研究成果已得到数学界广泛认可, 且已产生了两位菲尔兹奖得主(A. Connes和V. Jones), 5位国际数学家大会(ICM)的大会发言者(1978年的A. Connes; 1990年的Vaughan Jones; 1994年的D.Voiculescu; 2002年的U.Haagerup; 以及2006年的S.Popa)^[2]。

本文在分析梳理一些重要历史事件及主要成就的基础上, 厘清各个数学家之间的思想传承, 探讨冯诺依曼代数建立和发展的历史脉络。

1 理论的开始时期

冯诺依曼代数最初出现在冯诺依曼1929年发表于《数学年刊》的一篇论文^[3]中。文中，冯诺依曼定义了一个被称之为“算子环”的数学研究对象, 并且证明了“算子环”的最基本定理——二次换位定理。在20世纪40年代后期, “算子环”与“W^*-代数”被交叉使用。在《Les algibresd′opdrateursdansl′espacethlbertien》^[4]中, J. Dixmier根据J. Dieudonne的提议称这样的代数为“冯诺依曼代数”。冯诺依曼代数的定义如下。

定义1  设H是一个复希尔伯特空间, B(H)是H上所有有界线性算子构成的集合。B(H)的一个子集A称为^*-子代数, 如果A满足

对任意a, b∈A, λ∈C, λa, a+b, ab, a^*∈A,

这里a^*表示算子a的共轭算子。一个^*-子代数A称为是有单位的, 如果A包含单位算子1。B(H)的一个有单位的^*-子代数A称为一个冯诺依曼代数, 如果它满足下面的性质:

对于A中任一网{a_i:i∈Λ}, 如果存在a∈B(H)使得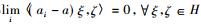, 则a∈A。

注1:

1) 如果B(H)中的子集具有上面的拓扑性质, 则称该子集是关于弱算子拓扑封闭的。

2) 上面的定义可以用来解释为什么冯诺依曼代数也被称为“W^*-代数”, W指的是弱算子拓扑, 而*指的是冯诺依曼代数关于共轭运算是封闭的。

3) 上面的定义称为解析或拓扑定义, 因为它是通过^*-子代数的拓扑性质来定义的。

冯诺依曼的二次换位定理表明，可以用一个有单位的^*-子代数的代数性质来定义冯诺依曼代数。

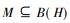
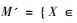
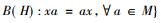
定义2  设, 集合 称为M的换位。

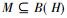
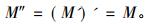
定理1(二次换位)   一个有单位的^*-子代数是冯诺依曼代数当且仅当

1935年, 因在线性算子和谱理论方面的研究刚获得哥伦比亚大学博士学位的青年数学家F. J. Murray来到普林斯顿, 有意在冯诺依曼的指导下从事(博士后)研究工作。Murray专注于因子M(即具有平凡中心的冯诺依曼代数: Z(M)=M∩M′=C1)的研究。他们最初的猜测主要是因子同构于B(H), H为某一希尔伯特空间。如果这一猜测成立，这将是一个非常有价值的结论, 也意味着该课题的结束。在第一年的合作研究中, 他们发现冯诺依曼代数是一个丰富且具有激发性的数学“世界”。

由冯诺依曼约化理论, 对一般冯诺依曼代数的研究可约化为对因子的研究。在研究因子过程中, 对因子中的投影(即自伴幂等算子)的研究就像为走进因子世界的迷宫打开了一扇大门。设M是一个因子, 一个投影e∈M称为极小的, 如果对于任何值域包含在e的值域中的投影f∈M (即, fe=f, 称f≤e), 有e=f。在一定意义下, 冯诺依曼代数中具有极小值域的投影是极小的。两个投影p, q称为互相正交的, 如果pq=0。下面这个结论表明Murray-von Neumann关于因子同构于B(H)的猜想只对某些特殊的因子成立。

定理2  如果因子M有极小投影, 那么存在希尔伯特空间H, 使得M同构于B(H)。

这样的因子(具有极小投影的因子)称为Ⅰ型因子。接下来面对Murray和冯诺依曼来说, 一个问题是:是否存在没有极小投影的因子?他们通过利用遍历理论技巧在两篇关于算子环的论文^{[1, 5]}中构造出没有极小投影因子的例子, 从而给出这一问题的肯定回答。

为了分类其他非Ⅰ型因子, Murray和冯诺依曼产生了对比投影(值域)“大小”的想法。两个投影p, q∈M称为是等价的, 如果存在算子v∈M将p的值域等距地映到q的值域上, 即v^*v=p, vv^*=q。投影间的这种等价关系记为p~q。当e~f₀, f₀≤f，记为e≤f。一个投影e∈M称为无限的, 如果e与e的某子投影e₀是等价的(即e~e₀, e₀≤e, e₀≠e)。否则, 一个投影e∈M称为是有限的:如果e与其任何真子投影都不等价。一个冯诺依曼代数M是有限的, 如果其单位元1∈M是有限的。

一个因子称为Ⅱ型的, 如果其没有任何(非零)极小投影, 但具有非零有限投影(如果单位算子1∈M是有限的则是Ⅱ₁型因子; 否则称为Ⅱ_∞型)。最后一种情形, 如果一个因子M没有非零有限投影, 则称M是Ⅲ型的。

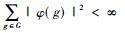
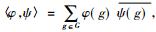
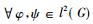
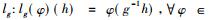
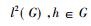
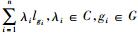
Murray和冯诺依曼利用群表示技巧构造了另一类非Ⅰ型因子的例子。设G是一个无限离散群, H是由G上所有满足条件的复值函数φ构成的希尔伯特空间, 记为l²(G)。l²(G)中的内积定义为 。对任意g∈G, 可如下定义l²(G)上的酉算子 。由生成的冯诺依曼代数称为G的群冯诺依曼代数, 记为L(G)。

下面的定理表明，可以通过上面的构造得到Ⅱ₁型因子。

定理3   冯诺依曼代数L(G)是Ⅱ₁型因子当且仅当群G是i.c.c(即:每一非单位元g∈G的共轭类{h^-1gh:h∈G}是一个无限集)。

Murray和冯诺依曼发现了两个i.c.c群。一个是F_n, n(≥2)个非交换生成元生成的自由群。另一个是局部有限群Π=∪{S_n:n=1, 2, …}, 其中S_n是n个元素的对称群。

特别地, 他们于1943年在《关于算子环Ⅳ》^[5]一文中证明了下面的结论。

定理4   L(Π)与L(F_n)(n≥2)不同构。

这表明不是所有的Ⅱ₁因子都是彼此同构的。换句话说, 至少存在两个不同的(非同构的) Ⅱ₁型因子。那么一个问题是:究竟有多少Ⅱ₁型因子?该问题在25年之后被数学家们在《Acountable infinity of Ⅱ₁ factors》^[6]，《Uncountably many Ⅱ₁ factors》^[7]和《An uncountable number of Ⅱ₁ and Ⅱ_∞ factors》^[8]中解决:存在不可数多个非同构的Ⅱ₁型。这也足以说明冯诺依曼代数“世界”何其丰富!

2 Tomita-Takesaki的模理论

Murray和冯诺依曼证明了一个因子是Ⅰ, Ⅱ, Ⅲ型的，当且仅当它的换位也分别是Ⅰ, Ⅱ, Ⅲ型的。但同一类型的因子可能具有完全不同的大小。例如, 冯诺依曼代数B(H), 这里H是可分无限维希尔伯特空间, 具有非常小的换位C1, 这是因为B(H)包含每一个在H上的冯诺依曼代数, 而每一个冯诺依曼代数都包含C1。

问题1   如何去选择一个冯诺依曼代数因子M的表示(即选择一个希尔伯特空间H使得M同构于B(H)的一个子代数)使得M和它的换位M′作用在表示希尔伯特空间H上具有同样的大小?

设M是作用在希尔伯特空间H上的冯诺依曼代数。如果存在向量ξ∈H使得Mξ和M′ξ都在H中稠密, 那么称冯诺依曼代数M具有标准形式。一个冯诺依曼代数具有标准形式的重要性体现在下面的结论中。

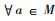
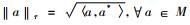
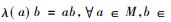
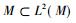
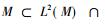
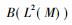
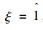
定理5  如果作用在希尔伯特空间H上的两个冯诺依曼代数M, N具有标准形式, 那么这两个冯诺依曼代数之间的同构π一定具有下面特殊的形式:存在H上的酉算子u使得π(a)=uau^*, 。可以通过下面的方式得到一个II₁型因子的标准形式。设M是一个因子且其上具有(正规的, 忠实的)迹态τ(这指的是τ:M→C是一个线性泛函, τ(1)=1, τ(a^*a)>0, ∀a∈M, a≠0, τ(ab)=τ(ba), ∀a, b∈M, 且τ满足一定的连续性)。我们可以在M上定义内积, (a, b)=τ(b^*a), ∀a, b∈M。这样我们在M上得到一个(向量)范数: 令L²(M)为M按照如上范数完备化所得到的希尔伯特空间。通过左乘: 得到一个表示λ:M→B(L²(M))。将M和λ(M)视为同一, 则有 。M具有生成向量, 这里1是M中的单位算子, 表示1在L²(M)中的像。因为Mξ=M在L²(M)中稠, 可以证明Mξ也在L²(M)中稠。因此, M作用在L²(M)上具有标准形式。

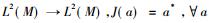
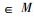
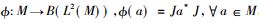
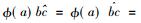
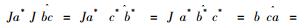
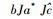
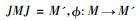
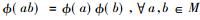
一个具有标准形式的Ⅱ₁型因子有下面特殊的性质。设Ⅱ₁型因子M作用在L²(M)上, 定义共轭线性映射J: 。则‖J(a)‖_τ²=τ(aa^*)=τ(a^*a)=‖a‖_τ²。由此得J:M→M是一个等距。因此, 可以将J扩展成L²(M)上的一个共轭线性同构。定义映射。则对任意a, b, c∈M, 有 。这意味着Ja^*J∈M′。Murray和冯诺依曼证明了是一个^*反自同构(即)。利用他们发展起来的技巧, Murray和冯诺依曼可以将这个结论推广到所有的Ⅰ, Ⅱ型因子:在标准形式下每个都是^*-反自同构于它的换位, 即它们具有相同的“大小”。Ⅲ型因子超出了他们的能力所及, 但这个问题在Ⅲ型因子情形下有什么答案呢?

1967年, 在巴吞鲁日的路易斯安娜州立大学举办的算子代数理论及其应用的一个大会上, M. Tomit作了题为《冯诺依曼代数的标准形式》^[9]的报告, 给出了这一公开问题的肯定回答。数学家M.Takesaki参加了该会议并在之后的一年时间访问了宾夕法尼亚大学(1968—1969)。Takesaki细化了Tomita的工作并将其与平衡态分析结合, 于1970年在《Tomira′s theory of modular Hilbert algebras and its applicattons》^[10]创立了Tomita-Takesaki模理论, 而这是20世纪70年代冯诺依曼代数主流研究课题。

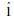
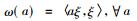
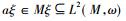
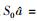
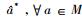
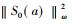
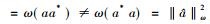
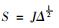
设M是一个冯诺依曼代数且其上有忠实的正规态ω。正如对Ⅱ₁型因子上的迹态所做的一样，可以通过左乘在L²(M, ω)上表示M。那么ξ= 是M的一个生成向量, 且 ∈M。Tomita的核心思想是考虑M和M′中的共轭运算, 通过ξ将他们约化到希尔伯特空间层次。我们利用来表示。定义 。注意到, 在这种情形下, , 因为ω并不一定是一个迹态。实际上, S₀是L²(M, ω)上一个稠定的闭(可能无界的)共轭线性算子。令为S₀的闭包S的极分解, 这里Δ=S^*S是一个(一般是无界的)自伴算子。J是L²(M, ω)上的一个共轭线性等距。当ω是一个迹时, S₀是一个等距, Δ=S^*S=1, 这便是在前面构造的Ⅱ₁型因子的标准表示。下面是Tomita的主要结论。

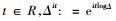
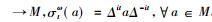
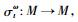
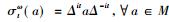
定理6  对任意是 。设 。映射t|→σ_t^ω是从加群R到M的^*-自同构群的一个同态，称σ_t^ω是忠实正规态ω的模群，且JMJ=M′。

这给出了Murray和冯诺依曼问题的肯定回答:如果一个冯诺依曼代数M具有标准形式, 那么M和M′是*反自同构的。

在回答Murray和冯诺依曼问题的过程中, Tomita发现了模自同构群。在对模理论的研究中, A.Connes在《UneclassiCcation des facteurs de type Ⅲ》^[11]中详细分析了该理论的构造并发现该理论为Ⅲ型因子的分类提供了许多新的强大的工具。

3 Connes关于内射因子的分类

在Tomita-Takesaki模理论的基础上, A.Connes定义了下面的不变量并对冯诺依曼代数因子进行了分类。

给定一个因子M, Connes定义S(M):=∩{σ(Δ_ω):ω是M上忠实正规态}, 这里σ(A)表示算子A的谱。他接着对Ⅲ型因子进行了如下的分类。

定理7  设M是一个因子。则

1) 0∈S(M)当且仅当M是Ⅲ型的; 且

2) 如果M是Ⅲ型的, 则只存在3种情形:

① M是Ⅲ₀型的, 如果S(M)={0, 1};

② M是Ⅲ_λ型的, 如果S(M)={0}∪{λⁿ:n=0, ±1, ±2, …}, 其中0 < λ < 1;

③ M是Ⅲ₁型的如果S(M)=[0, ∞)。

一个冯诺依曼代数称为是超有限的, 如果存在M的有限维冯诺依曼子代数列M_n, 这些子代数按照包含关系是全序的, 并且他们按弱算子拓扑在M中稠。Murray和冯诺依曼在于1943年证明了所有超有限Ⅱ₁型因子是同构的。这个唯一的超有限Ⅱ₁因子记为R。一个作用在希尔伯特空间H上的冯诺依曼代数M称为是内射的, 如果存在一个从B(H)到M上的范数为一的投影。

在所有的因子中, Connes确定了一类(相对)容易研究的因子:内射因子。他于1976年在《内射因子的分类》^[12]中证明了一个Ⅱ₁型因子M是超有限的当且仅当它是内射的。他得到了(本质上完全的)内射因子的分类。

定理8  考虑作用在可分无限维希尔伯特空间上的因子。在同构意义下,

1) 存在唯一的Ⅱ₁型内射因子R;

2) 存在唯一的Ⅱ_∞型内射因子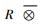 B(l²(N));

3) 对每个0 < λ < 1, 存在唯一的Ⅲ_λ型内射因子R_λ;

4)Ⅲ₀型内射因子与“权流(flows of weights)”是一一对应的。

其中“权流(flows of weights)”是遍历理论中的一个重要技术概念。

Ⅲ₁型因子的分类工作是由U.Haagerup在文《Connes′ bicentralizer problem and uniqueness of the injective factor of type Ⅲ₁》^[13]中完成的, 给出如下结论:

定理  存在唯一的Ⅲ₁型内射因子。

4 结语

结构化是20世纪数学发展的一大特色^[14]。冯诺依曼代数是一类由希尔伯特空间上的有界线性算子组成的代数, 是20世纪数学抽象化结构化统一化趋势下的产物。冯诺依曼为了将非交换环理论推广到希尔伯特空间的情形, 引进算子环概念, 促使一个新的重要数学领域——冯诺依曼代数的诞生。这不仅为量子力学奠定了数学基础, 也引起了众多数学家关注这一领域, 产生了许多新理论。Tomita-Takesaki理论、Connes关于顺从von Neumann因子的分类工作使得von Neumann代数不断发展完善, 并形成以Voiculescu的自由概率论和S. Popa的关于Ⅱ_-1因子分类的刚性和变形理论为主的当代von Neumann代数最活跃的两个研究领域。