2. 河北师范大学 数学与信息科学学院, 河北 石家庄 050024;
3. 西北师范大学 教育学院, 甘肃 兰州 730070
2. College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024, China;
3. Educational Institute, Northwest Normal University, Lanzhou 730079, China
拉格朗日(Joseph Louis Lagrange, 1736—1813)是变分法的主要缔造者之一。18世纪50-60年代, 他通过首创“变分”概念、引进新符号δ及其演算而发明的“变分方法”——δ-算法, 堪称变分法早期发展中的一次变革, 将此前瑞士数学家欧拉(Leonard Euler, 1707—1783)所提出的依赖于几何的繁复方法最终变成了一种纯分析的、简捷优美的形式演算, 同时该方法将自牛顿(Issac Newton, 1643—1727)以来通过改变极值曲线上个别坐标以获取比较曲线, 转变为以整条曲线的改变获得比较曲线, 从而开创了一般意义上的变分方法, 使其变分法研究迥别与欧拉等数学家的研究思路, 将早期变分法的发展推进到一个新的发展阶段[1]。
截至目前, 已有戈德斯坦(Herman Heine Goldstine, 1913—2004)[2]、弗雷泽(Craig Fraser)[3]等学者对拉格朗日的变分法思想和工作进行了细致分析和考察, 从中可以看出, 拉格朗日早年在提出和阐述其新方法时经历了由非参数向参数表示形式的转变:1755年8月12日, 拉格朗日在写给欧拉的信中首次提出了其非参数形式的δ-算法[4], 而在5年后第一次公开发表的有关变分法研究的两篇论文“论确定不定积分公式的极大和极小的一个新方法”[5]和“可解不同动力学问题的方法——追前法之应用”[6]中, 拉格朗日却以参数表示形式阐述了其δ-算法。
在将δ-算法参数化的同时, 拉格朗日还对变分法及应用也做出了一些重要推广或发展。由此自然会产生这样的问题:这种表述形式上的改变与他对变分法所作的推广或创新之间有无内在思想关联?显然, 此问题对于认识和把握拉格朗日早期变分法思想的演变具有极为重要的意义。然而, 据笔者所知, 以往相关研究对此却鲜有专门论述。本文在分析和阐明拉格朗日δ-算法非参数表示和参数表示的基础上, 立足其早年的相关信件及论文等原始文献, 重点探讨在参数化改造过程中拉格朗日对变分法理论及应用所作的革新与发展。
1 拉格朗日首次提出的δ-算法——非参数表示在1744年出版的《求某种具有极大或极小性质曲线或解最广义等周问题的技巧》(下简称《技巧》)[7]一书中, 瑞士数学家欧拉(Leonard Euler, 1707—1783)虽已推导并确认出了几类非参数形式表述的变分问题的标准微分方程, 但其几何与分析相结合方式建立变分问题微分方程的做法, 使得推演过程非常繁复, 同时还隐含着微分符号d的双重含义和混用状况。为改进和简化欧拉推导变分问题微分方程的方法, 消除其方法中符号d的双重意义和混用现象, 拉格朗日在1755年8月12日写给欧拉的信中首次提出了其“变分方法”——δ-算法。
拉格朗日的这种方法, 其核心是在当时的微积分演算中引进符号δ及其演算。他用符号δ表示与通常微分d不同的、另一种形式的微分——“变分”, 用现在术语来说, δ表示的是泛函自变量(即函数)的增量或者由此增量所引起的泛函增量的一次项。拉格朗日本人当时侧重于将δ视作一种形式演算, 指出δ不仅可作用于诸如f(x, y, y′, y″, …, y(n))(其中y是x的函数)这样的函数上, 还可以作用于需要求极值的积分上, 变分运算δ与通常微分运算d具有相类似计算方法和运算规则, 且δ和d,δ和积分运算∫可交换运算次序, 即dδ=δd, δ∫=∫δ成立。
值得注意的是, 拉格朗日此时主要基于端点固定、非参数形式表述的变分问题阐述了其所创的δ-算法。他将容许的比较曲线与所求极值曲线均看作是以x为自变量、以y为因变量的函数, 此时问题中变量x和y的地位并不平等, 突出表现在他事先特别假定了作为自变量的变量x关于δ运算恒定不变, 即δx=0, 由此显见δdx=dδx=0。
拉格朗日δ-算法的基本精神主要体现在对变分问题微分方程的推导过程中, 因此我们以其信中第一个问题为例进行说明①。
① 拉格朗日当时的符号与现代略有不同:他用因变量和自变量的微分之比(即微商)以及微分系数来表示其中未知函数的各阶导数, 积分号中未明确标出积分上、下限; 此外, 为计算简便起见, 他将自变量x的微分dx形式地视作常数1, 将积分写为∫Z, 其中被积函数Z形式地视作x, y, dy, d2y, …的函数。为清楚起见, 本文均将其改为现在熟悉的符号形式。
问题1 在端点固定的条件下, 寻求x和y之间的函数关系式y=y(x), x∈[a, b], 使得积分J=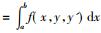
② 事实上, 拉格朗日是针对更一般情形(即在变分积分中含有未知函数高阶导数的情形)进行阐述的, 为简明起见, 本文均以含未知函数一阶导数的情形进行说明。
拉格朗日的总体思路是由积分J的变分δJ=0导出变分问题的微分方程。为此他基于δ-演算规则, 借助假定δx=0, 首先计算出
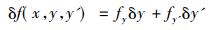
|
(1) |
接着由δ和积分运算∫的可交换性得到变分
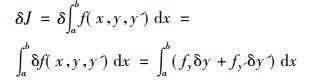
|
(2) |
又由d和δ两个运算次序的可交换性以及δdx=0知δy′=δ(dy/dx)=d(δy)/dx。对(2)中第二项分部积分, 拉格朗日得到如下变分表达式
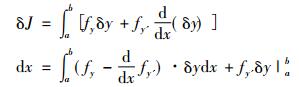
|
(3) |
由于假定端点固定, 因此在端点x=a, x=b处, δy=0, 从而有
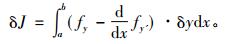
|
拉格朗日认为对于极大或极小化函数而言, 应有δJ=0, 由此直接断言上式积分号下δy的系数为0, 由此推得该变分问题的微分方程(即现在所称的欧拉方程)③
③ 尽管拉格朗日认为由δJ=0可得出积分号下δy的系数为0, 但历史上对此事实的第一个正确证明直至1848年才由法国数学家撒吕斯(P. F. Sarrus, 1789—1861)给出, 此结果就是现在所称的变分法基本引理。
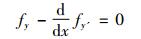
|
(4) |
信中拉格朗日还对《技巧》中其他两类更为复杂的问题进行了讨论, 运用δ-算法不仅导出了欧拉已得到的微分方程, 而且还大大简化了其推导过程。需要指出的是, 在讨论这两类问题时, 拉格朗日同样以非参数观点阐述了其δ-算法。
2 拉格朗日第一次公开发表的δ-算法——参数表示拉格朗日δ-算法首次公开发表在1760年的论文“论确定不定积分公式的极大和极小的一个新方法”中。在这篇论文开始部分, 拉格朗日首先简要回顾了变分法这门学科的早期历史, 同时明确指出欧拉方法“尚缺乏一门纯分析学科所要求的那种高度的简明性……, 需有一种能摆脱几何论证的方法”[8]。接着在论文主体部分, 他主要围绕三类变分问题对其δ-算法进行了阐述。然而与1755年情形不同的是, 这次他是用参数观点或者说是结合参数形式的变分问题进行阐述的, 即将所考虑的比较曲线与所求极值曲线均看作是由参数方程形式表示的, 并将原来极值曲线为平面曲线的变分问题推广到空间曲线情形。下面我们仍以其第一类问题为例进行说明。
问题1 已知定积分表达式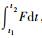
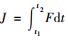
拉格朗日解决问题的思路与1755年信中的基本相同, 不同的是, 此时他将考虑的极值曲线, 由原来非参数表示形式转变为参数方程表示形式:x=x(t), y=y(t), z=z(t)。根据δ和∫运算的可交换性, 他首先积分J取极值的必要条件变为
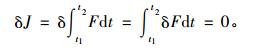
|
为计算积分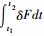
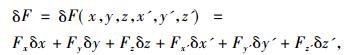
|
(5) |
由于此时采用的是参数表示形式, 因而问题中变量x, y, z地位平等, 均为参数t的函数, 从而式(5)中δx,δy,δz的地位也平等, 因此拉格朗日并未像1755年那样事先假定δx=0。事实上, 通过参数表示(此时t作为自变量), 他将原来δx=0的假定隐含地转变成了δt=0(从而有δdt=dδt=0)。由d和δ两运算次序的可交换性以及分部积分, 他进而得到
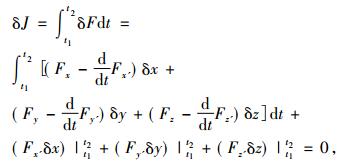
|
(6) |
由方程(6), 拉格朗日得出如下两个方程
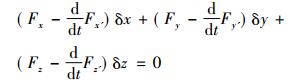
|
(7) |
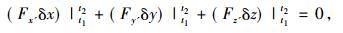
|
(8) |
并称方程(7)为“不确定方程”, 方程(8)为“确定方程”。当δx,δy,δz完全独立时, 由“不确定方程”(7)可得所求极值曲线满足如下微分方程组
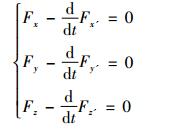
|
(9) |
方程组(9)是拉格朗日导出的极值曲线应满足的基本微分方程组①, 而其“确定方程”(8)是极值曲线所满足的端点条件②, 当端点固定时, 方程(8)显然成立, 而当端点变动时, 由方程(8)可导出极值曲线与端点曲线或曲面所满足的横截条件。
① 需注意的是, 拉格朗日由方程(6)推导方程组(9)和端点条件(8)的过程并不是现代严格正确的推导过程。现代严格的推导思路如下:假定δx, δy, δz是独立的, 先取两端点固定的曲线弧子集合, 方程(6)对于此子集合中的任意一条曲线弧而言是成立的, 此时方程(6)中积分号外的项为0, 由变分法基本引理, 可得方程组(9);然后再将比较曲线类扩展到最初的曲线集合时, 由于方程组(9)成立, 因而方程(6)中的积分项为0, 由此可推得端点条件方程(8)。现代严格的推导不会出现方程(7), 具体可参见文献[9]。
② 拉格朗日将方程(8)写为′M-M′=0, 其中′M、M′分别表示(Fx′δx)+(Fy′δy)+(Fz′δz)在t1、t2处值。
3 拉格朗日在参数化过程中对变分法及应用所作的革新与发展拉格朗日在将其δ-算法参数化的过程中, 对变分法及应用做出了一些重要推广和发展, 主要表现在以下几方面③ :
③ 需要指出的是, 除下文中所列举的几项推广或发展外, 拉格朗日还在第一篇论文后的附录Ⅰ中对极小曲面问题进行了探讨, 导出了极小曲面所满足的偏微分方程, 此项工作实际上开启了变分法中多重积分极值问题的研究。由于拉格朗日的这一开创性贡献与本文所论主题关系不大, 故在此不再赘述。
1) 变分问题的推广。在欧拉《技巧》一书和拉格朗日1755年8月的信中, 所论变分问题均为变分积分中只含一个一元未知函数的情形, 此外, 欧拉在《技巧》中对极值曲线的端点条件并未特别关注, 拉格朗日在其信中也只是讨论了端点固定情形。但通过参数化改造后, 从数学形式上看, 拉格朗日却将此前只依赖于一个一元未知函数变分问题的研究推广到含多个一元未知函数情形变分问题的研究, 同时将固定端点变分问题的讨论推进到包括端点可变动变分问题的讨论。对变动端点问题, 尽管在拉格朗日以前, 牛顿(Issac Newton, 1643—1727)、约翰·伯努利(John Bernoulli, 1667—1748)等人已有所触及, 但拉格朗日参数形式的δ-算法为一般地处理此类问题提供了便利。
2) 变分方程的推广。欧拉和拉格朗日变分法的根本思想是希望把变分问题化归为微分方程, 再进而求解。不过他们两人最初只是导出了变分积分中含一个一元未知函数变分问题的微分方程(如方程(4)等), 而拉格朗日通过参数表示后, 导出了变分积分中含多个一元未知函数变分问题极值曲线所满足的微分方程组(如方程组(9)等), 这种微分方程个数从“一”到“多”的推广, 为将变分问题及其极值曲线的讨论从平面曲线情形扩展到三维乃至更高维空间曲线情形铺平了道路。
3) 首次完整而明确地导出端点条件(即他所称的“确定方程”(8)), 并藉此从一般角度探讨了变端点变分问题的横截条件。横截条件作为变端点问题基本微分方程(组)的必要补充, 在变分法中具有重要作用, 因为就具体的变端点变分问题而言, 在极值曲线存在的前提下, 只有将横截条件和基本方程(组)等结合起来, 才能最终确定出特定的极值曲线。虽然在1755年8月12日的信中, 拉格朗日已导出了包含端点项的变分表达式(即(3)), 由此表达式可得到如下端点条件
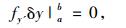
|
但此条件只适用于端点固定(此时在端点处有δx=0, δy=0)或端点在两垂直于x轴的直线x=a,x=b上变动的情形(此时在端点处有δx=0, δy≠0), 而不适用于一般变动端点问题(此时在端点处有δx≠0, δy≠0)。在第一篇论文中, 拉格朗日通过参数化表示而最终导出的端点条件(8), 不仅适用于端点固定情形, 而且适用于端点任意变动情形。为说明其一般性, 他还以空间中变端点最速降线问题为例, 在所获端点条件的基础上, 得到了极值曲线与端点曲线或曲面在交点处成立的横截条件。
事实上拉格朗日本人对自己在变分法上所作的上述推广有十分清晰的认识。对此, 他在1760年的第一篇论文中这样写道:
“欧拉虽是给出求解如下问题一般公式的第一人:求一条曲线, 使得沿此曲线一给定积分取极大或极小值, …, 但这位作者的公式并没有我们的普遍:一是因为他只允许积分的被积函数Z中单个变量y变化; 二是因为他假定曲线起点和终点固定。”([5], 第345页)
4) 变分法力学应用——最小作用原理的推广。
基于对自然界经济本性的信仰和论证上帝存在的神学目的, 18世纪40年代, 法国科学家莫培都(P.L.M. Maupertuis, 1698—1759)在费马(Pierre Fermat, 1601—1665)最小时间原理(1657)、约翰·伯努利虚速度原理(1717)以及自己提出的静止定律(1740)等相关研究基础上, 率先提出了著名的最小作用原理[10-12], 但其论述仍存在许多模糊之处。
大约同期, 欧拉在《技巧》附录2中首次给出了有心力场中单个质点沿平面曲线运动的最小作用原理的精确表述, 拉开了变分法在力学中广泛应用的序幕。
拉格朗日则将欧拉最小作用原理的研究推向了一般情形。在1760年发表的第二篇论文中, 通过参数表示(即将空间中运动质点的位置坐标表示为独立参数(如时间等)的函数), 他将此前欧拉的最小作用原理推广到空间中相互作用的保守质点系情形, 在此基础上展示了依δ-算法推导质点或质点系运动方程的统一方法, 并籍此解决了大量动力学具体问题[13]。
4 结语拉格朗日早年变分法从非参数形式向参数形式的转变, 为其将变分问题的讨论从平面曲线情形扩展到空间情形铺平了道路, 从而大大开阔了变分法研究和应用范围, 赋予了变分法在力学研究和应用中的重大价值, 同时也为后来变分法在微分几何等学科中的广泛应用奠定了基础。
不过需指出的是, 拉格朗日早年虽用参数观点表述和处理了变分问题, 同时对这种表述的优越性有所体察, 但其参数表述仍有一些缺陷或不足。譬如, 他从未讨论过参数和非参数这两种表述形式之间的区别, 也没有注意到参数情形下变分积分的被积函数f必须满足的条件, 如, 被积函数f中不显含参数, f是未知函数x, y, z时导数x′,y′,z′的正一次齐次函数等[14], 这些条件以及对参数形式变分问题的系统处理, 直至19世纪80年代, 才由德国数学家魏尔斯特拉斯(Karl Weierstrass, 1815—1897)给出[15]。当然我们不能因此而过分苛求于拉格朗日, 无疑其工作具有极为重要的开拓和先导意义。
| [1] |
贾小勇, 李跃武. 变分法的一次变革:从欧拉到拉格朗日的形式化改造[J]. 自然科学史研究, 2009, 28(3): 312-325. DOI:10.3969/j.issn.1000-0224.2009.03.005 |
| [2] |
GOLDSTINE H H. A History of the Calculus of Variations from the 17th Through the 19th century[M]. Berlin/New York: Springer-Verlag, 1980: 110-138.
|
| [3] |
FRASER C. J. L.. Lagrange's changing approach to the foundations of the calculus of variations[J]. Archive for History of Exact Sciences, 1985, 32: 151-191. DOI:10.1007/BF00329871 |
| [4] |
LAGRANGE J L. Letter to Euler 12 August 1755[M]//Serret J A(eds). Oeuvres de Lagrange. Vol. XIV. Paris: Gauthier-Villars, 1892: 138-144.
|
| [5] |
LAGRANGE J L. Essai D'une Nouvelle Methode Pour Determiner Les Maxima et les Minima Des Formulas Indefinies[M]//Serret J A(eds). Oeuvres de Lagrange.Vol.Ⅰ, Paris: Gauthier-Villars, 1867: 335-362.
|
| [6] |
LAGRANGE J L. Applications de la Methode Exposee Dans le Memoir Precedent a la Solution de Differents Problemes de Dynamique[M]//Serret J A(eds). Oeuvres de Lagrange.Vol. Ⅰ, Paris: Gauthier-Villars, 1867: 363-468.
|
| [7] |
EULER L. Methodus Inveniendi Curvas Lineas Maximi Minimive Proprietate Gaudentes Sive Solution Problematis Isoperimetrici Latissimo Sensu Accepti[M]. Lansanne: Bousque, 1744.
|
| [8] |
李文林. 数学珍宝——历史文献精选[M]. 北京: 科学出版社, 1998: 356-362.
|
| [9] |
拉弗林契叶夫M.A., 留斯切尔涅克A.变分学教程[M].曾鼎鉌, 王梓坤, 译.北京: 高等教育出版社, 1954.
|
| [10] |
PANZA M. The Origins of Analytic Mechanics in the 18th Century[M]//Jahnke, H. N(eds). History of Analysis.AMS, LMS, 2003: 137-153.
|
| [11] |
MACH E. The Science of Mechanics: A Critical and Historical Account of Its Development[M]. Chicago/London: Open Court Publishing Co, 1919.
|
| [12] |
GRIGORIAN A T. On the development of variational principles of mechanics[J]. Archives Internationals D'histoire Des Sciences, 1965, 18: 23-35. |
| [13] |
FRASER C.J. L.. Lagrange's Early contributions to the principles and methods of mechanics[J]. Archive for History of Exact Sciences, 1983, 28: 197-241. DOI:10.1007/BF00328268 |
| [14] |
GIAQUINTA M, HILDEBRANDT S. Calculus of Variations Ⅱ The Hamiltonian Formalism[M]. Berlin: Springer-Verlag, 1996.
|
| [15] |
WEIERSTRASS K. Vorlesungen über Variationsrechnung(1865—1890)[M]//Rothe R(eds). Mathematische Werke. Vol. Ⅶ, Leipzig: Akademische Verlagsgesellschaft, 1927.
|
 2017, Vol. 47
2017, Vol. 47
 , 贾随军3
, 贾随军3