在现实生活中, 语音信号会被不同的噪声干扰和污染。语音增强可以从被污染的语音信号中提取尽可能纯净的语音, 改善语音质量, 提高语音可懂度和清晰度。麦克风阵列是由一组麦克风按照一定空间分布规则布置而形成的阵列。将麦克风阵列运用于语音增强处理, 对接收到的语音信号按照空间分布规律进行有针对性的算法处理, 可以进一步增强有用的语音信号, 抑制噪声和干扰。
文献[1]提出了基于广义旁瓣抵消器(Generalized sidelobe canceller, GSC)的降噪算法, 该算法结构简单, 容易实现, 广泛应用在各种阵列信号处理中。文献[2]提出了基于传递函数的广义旁瓣抵消器算法(Transfer function generalized sidelobe canceller, TF-GSC)。与传统的GSC算法相比, TF-GSC算法是一种高效的、低计算的解决方案, 可实现多通道语音信号增强。该算法通过利用声学传递函数系数比例代替传递函数系数, 从而构建新的阻塞矩阵, 并使用在频域的相乘传递函数(Multiplicative transfer function, MTF)近似形式建立阵列信号传递函数模型, 这可以处理任意声学传递函数。文献[3]和文献[4]引入了一种在短时傅里叶变换域中的卷积传递函数(Convolutive transfer function, CTF)近似的相对传递函数(Relative transfer function, RTF)识别方法[5], 提出了卷积传递函数广义旁瓣抵消器算法(Convolutive transfer function generalized sidelobe canceller, CTF-GSC), 该算法用CTF近似形式代替TF-GSC算法中的MTF近似形式, CTF近似形式比MTF近似形式估算更加准确,且有更少的限制要求, 进一步提高了语音系统的降噪能力。
波束形成算法对于相干性噪声的抑制能力很好, 但是对于非相干性噪声的消除就不太明显。所以, 在后来的研究中, 一些研究者引入后置滤波算法, 增强了语音系统的抑制噪声能力。文献[6]提出了一种处理非平稳噪声的方法, 该方法在后置滤波段利用最小控制递归平均算法(Minima controlled recursive averaging, MCRA)估计噪声。文献[7]对MCRA做了改进, 提出了一种改进的最小控制递归平均算法。该方法能在复杂环境下估计噪声。文献[8]将GSC和最佳修正对数谱幅度估计结合起来, 利用GSC的输出信号和参考噪声的相互关系进行后置滤波。文献[9]在此基础上进一步改进, 用TF-GSC结构代替GSC结构, 相对而言, TF-GSC结构能使波束形成自适应指向目标语音信号的方向, 该算法性能更稳定。文献[10]提出了一种在混响环境下基于检测和估计方案的多通道后置滤波算法。该算法改进了信号存在概率, 提出新的计算直接混响比估计器, 适应于远程讲话场景。文献[11]将TF-GSC算法后置维纳滤波结合,可以同时抑制早期反射噪声、后期混响和环境非相干噪声。
在CTF-GSC算法的自适应噪声抵消器模块中, 文献[3]采用了归一化最小均方(Normalized least mean square, NLMS)算法, NLMS算法是一种自适应滤波算法, 已广泛应用于许多信号处理应用中。由于其简单性, NLMS算法[12]是目前最流行的自适应滤波算法。基本NLMS的稳定性由固定步长μ控制。该参数还控制收敛速度、跟踪能力速度和稳态均方误差量。对于复杂环境中的一些非相干性噪声, CTF-GSC算法的性能严重降低, 而基于维纳滤波的后置滤波算法[13-14]对环境中的非相干性噪声有明显的抑制效果。
本文在CTF-GSC算法的基础上, 提出基于变步长NLMS的CTF-GSC算法与优化的后置滤波算法相结合的麦克风阵列的语音增强算法。在改进的后置滤波算法中, 引入语音活动检测和小波阈值多窗口谱估计对噪声信号进行估算。新的算法对相干性噪声和非相干性噪声都有很好的抑制效果, 尤其在混响环境下, 提高系统信噪比,以及降低语音失真, 鲁棒性更好。
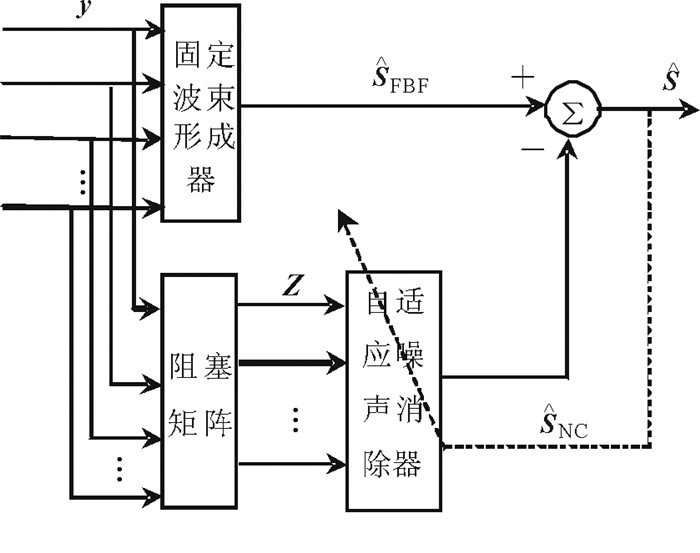
1 基于CTF-GSC的麦克风阵列语音增强算法 1.1 基本的CTF-GSC算法CTF-GSC算法的基本结构框图如图 1所示, 它由3部分组成:固定波束形成器(Fixed beam foming, FBF)、阻塞矩阵(Blocking matrix, BM)和自适应噪声抵消器(Adaptive noise canceler, ANC)。CTF-GSC算法是以传统GSC算法为基础, 考虑不同频率之间的互相干扰, 使用各个麦克风之间的相对传递函数的比例系数[5](Relative transfer functions, RTFs)对固定波束形成器和阻塞矩阵进行新的构造, 利用在频域的CTF近似形式建立阵列信号传递函数模型。
|
图 1 CTF-GSC算法结构框图 Fig. 1 CTF-GSC algorithm block diagram |
在嘈杂和混响的复杂环境下, 设有M个麦克风在工作, 只设置一个目标语音信号源。第i个麦克风所采集到的语音信号为

|
(1) |
其中, i=1, 2, …, M,*表示卷积, s(n)表示目标语音信号源, ai(n)表示目标语音信号源到第i个麦克风路径的传递函数, di(n)和ui(n)表示第i个麦克风所采集到的语音信号和噪声信号。
在CTF-GSC算法中,把CTF近似形式引用到传统的GSC算法的阻塞矩阵,其中,卷积矩阵满足Hi(k′, k)=0, ∀k′≠k。所以将阻塞矩阵[3]设计为
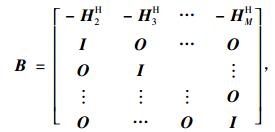
|
(2) |
并有

|
(3) |
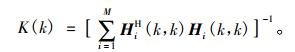
|
(4) |
则BM模块输出为
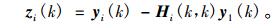
|
(5) |
其中,i=2, …, M。
FBF模块输出为
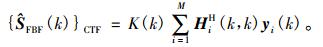
|
(6) |
在ANC模块使用NLMS算法对滤波器系数进行更新迭代[9],
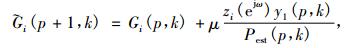
|
(7) |

|
(8) |
其中,

|
(9) |
在CTF-GSC算法中, 最重要的就是估算出各个麦克风所采集到的语音信号之间的RTFs, 即Hi(i=1, 2, …, M)。设第i个麦克风所采集到的带噪语音信号为yi(k), 第一个麦克风所采集到的带噪语音信号为y1(k)。所以有
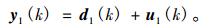
|
(10) |
根据STFT的矢量变换, 则每个麦克风所采集到的语音信号为
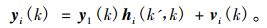
|
(11) |
其中, vi(k)表示第i个麦克风所采集到的噪声信号。当k′≠k时, hi(k′, k)=0, hi(k, k)表示各个麦克风所采集到的语音信号在相同频点上的相对脉冲响应, 且hi(k)=[hi(0, k), hi(1, k), …, hi(P-1, k)]T。
另有
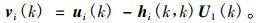
|
(12) |
其中, U1(k)表示由u1(k)的STFT系数构成的Toeplitz矩阵。
再对式(11)和式(12)等号两端的语音信号的第k帧同时求解互功率谱, 则有

|
(13) |
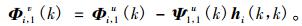
|
(14) |
因为语音信号s(n)与噪声信号u(n)互不相关, 所以Ψ1, 1y(k)=Ψ 1, 1s(k)+Ψ 1, 1u(k), 根据式(13)和式(14), 则有
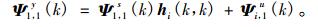
|
(15) |
根据功率谱密度(Power spectrum density, PSD)估计, 将式(15)改写为

|
(16) |
其中, e(k)表示PSD估计误差,

|
(17) |

|
(18) |
运用加权最小二乘法[3]对式(16)进行处理, 可以得到

|
(19) |
其中,Γ(k)表示权重矩阵,Φi, 1y(k)和Ψ1, 1y(k)可以通过所采集的语音信号计算, Ψ1, 1u(k)和Φi, 1u(k)可以从静默段得到。
1.2 改进的CTF-GSC算法文献[3]在CTF-GSC算法的ANC模块中, 使用了基本的固定步长NLMS算法来迭代更新滤波器系数。在式(7)中, μ表示步长因子, 控制自适应速度与稳定性。固定步长的NLMS自适应算法在收敛速率、跟踪速率及稳态失调噪声之间是相互矛盾的, 当μ取值较小时, 稳态失调噪声较小, 精度高, 但是收敛和跟踪速度较慢。为了克服这一缺点, 本文采用变步长归一化最小均方(Variable step-size normalized least mean square, VSS-NLMS)算法[12]来改进步长因子μ。

|
(20) |
其中,θ表示遗忘因子, λ表示增加了设计自由度的正参数, 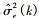
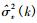

|
(21) |

|
(22) |
在式(22)中,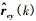
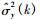
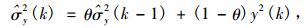
|
(23) |

|
(24) |
在ANC模块引用变步长NLMS算法迭代更新滤波器系数。改进的变步长NLMS算法可以进一步降低输入语音信号对噪声估计的影响, 使ANC系统具有更快的收敛性、更高的稳定性和更好的抑制干扰能力, 并使滤波器的输出信号与期望输出信号之间的均方误差最小, 这样系统输出为有用信号的最佳估计。从而使CTF-GSC算法对噪声的抑制能力更强。
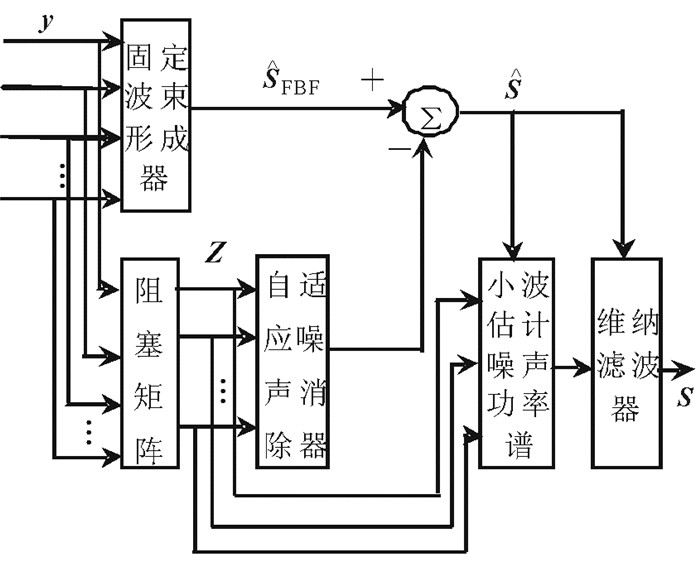
2 基于CTF-GSC和后置滤波的麦克风阵列语音增强算法在复杂的混响环境下, CTF-GSC算法不仅对相干性噪声有较好的抑制能力, 而且可以降低语音信号的失真。将改进的维纳滤波算法与CTF-GSC算法结合, 组成基于CTF-GSC的多通道后置滤波算法。本文提出的算法能够有效消除语音信号中的干扰噪声、降低语音失真、提高降噪性能。本文提出的基于CTF-GSC和后置滤波的麦克风阵列算法结构框图如图 2所示。
|
图 2 CTF-GSC结合后置滤波算法结构框图 Fig. 2 CTF-GSC combined post-filter algorithm block diagram |
如图 2所示, 在传统的基于先验信噪比的维纳滤波算法[14]的基础上, 通过引入语音活动检测(Voice activity detection, VAD)算法[15-16]和小波阈值多窗口谱估计算法[17],进一步改进了滤波器性能。
在改进的算法中, 先利用小波阈值多窗口谱估计算法对经CTF-GSC算法输出的语音信号
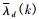
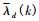

|
(25) |
判决参数β(p)的表达式为

|
(26) |
其中,a表示平滑系数, 在仿真实验中, 经过比较分析, a取经验值0.96。T表示固定阈值, 固定阈值在语音信号和噪声信号判决中起着重要的作用, 在仿真实验中, 经过大量比较分析, T取经验值0.16, < ·>表示求平均值。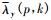
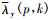
利用直接判决算法[18]对下一帧的先验信噪比更新, 计算公式为
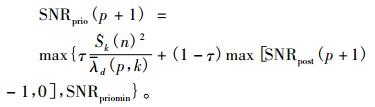
|
(27) |
其中,SNRpriomin通常设为-21dB,τ表示平滑系数, 一般取0.8~1之间, 在仿真实验中, 经过比较分析, τ取经验值0.98。
维纳滤波器的增益函数为
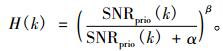
|
(28) |
其中, α和β表示噪声抑制因子, 在传统的维纳滤波算法中, α和β通常取值都为1。然而, 这一设定容易导致估算出的先验信噪比失准, 与实际先验信噪比存在较大偏差。经过实验分析和对比, 本文对维纳滤波算法进行了优化, 参数α的取值调整为
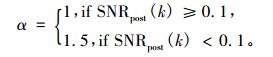
|
(29) |
经过大量实验分析比较, 设置参数β的取值根据α的变化而变化, β=1/α。
因此增强后的频域语音信号为
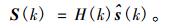
|
(30) |
对频域语音信号S(k)进行短时傅里叶逆变换, 然后合帧处理, 最后得到增强后的时域语音信号s(n)。
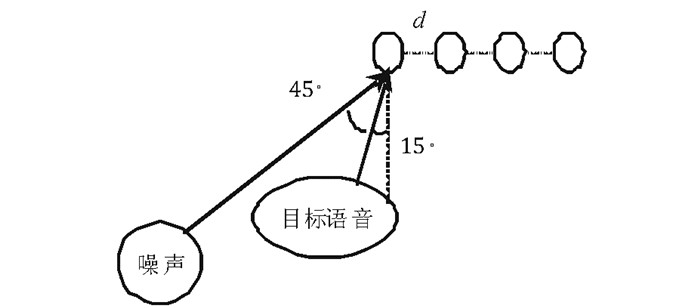
3 实验结果及分析利用Matlab软件对算法进行实验仿真测试。为进一步说明算法的性能, 将改进的变步长的NLMS算法与基本的固定步长的NLMS算法、改进的后置维纳滤波算法与传统的维纳滤波算法、本文所提出的新算法与TF-GSC算法, CTF-GSC算法进行了比较分析。在实验中, 麦克风采样频率为8kHz, 采用由4个麦克风组成的间距d=0.04m的均匀线性麦克风阵列。令左边的第一个麦克风为参考麦克风, 设置目标声源与麦克风阵列的垂直方偏角分别为0°和15°。目标声源为距离参考麦克风2m处的录音, 噪声源为与麦克风阵列成45°的录音。在两个位置模拟噪声信号源:其中一个噪声信号源相对靠近麦克风阵列, 产生相干性噪声; 另一个噪声信号源与麦克风阵列相对较远, 产生非相干性噪声。图 3为在噪声环境下麦克风阵列示意图, 加hamming窗, 窗长和帧长都为512, 帧移为256。为了方便比较, 式(20)中其他实验参数设置参照文献[12], 其中,θ=0.899 8, μ(0)=1, λ=30。
|
图 3 在噪声环境下麦克风阵列示意图 Fig. 3 Microphone array diagram in noise environment |
分段信噪比是先计算语音信号每一帧的信噪比, 再取整段语音信号中所有帧的信噪比平均值得到的。它的定义为

|
(31) |
其中,M表示语音信号帧数,m表示语音信号每一帧的采样点数,L表示语音信号帧长,sφ(n),sd(n)分别表示纯净语音信号和带噪语音信号。
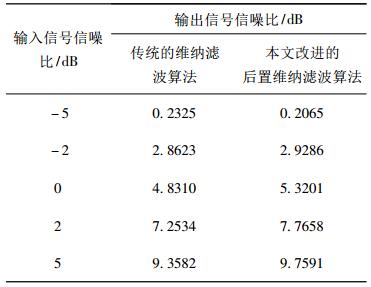
在高斯白噪声环境和相同的实验条件下, 改变的输入分段信噪比对含噪语音信号分别采用传统的维纳滤波算法和本文改进的后置维纳滤波算法进行语音增强的实验。其实验仿真结果如表 1所示, 从表中可以看出, 本文所改进的后置维纳滤波算法只有在信噪比很低的情况下(-5dB), 输出语音信号的分段信噪比增量才稍微低于传统的维纳滤波。在其他信噪比情况下, 经过本文所改进的后置维纳滤波算法增强的输出语音信号的分段信噪比增量比传统的维纳滤波算法都要高。从总体来说, 本文改进的后置维纳算法输出信号的分段信噪比平均增量都要高于传统维纳滤波算法。
|
|
表 1 输出信号的分段信噪比测量结果对比 Tab. 1 Comparison of measurement results of segmented signal to noise ratio of output signal |
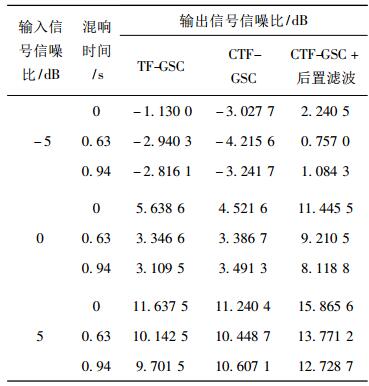
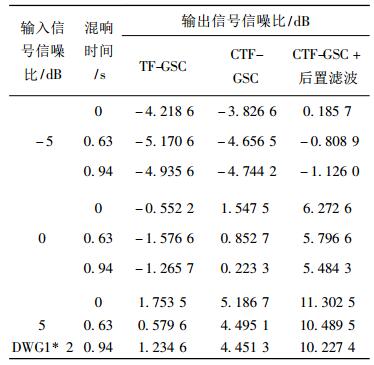
在相同的实验条件下, 改变输入分段信噪比、混响时间和偏角,对含噪语音信号分别采用TF-GSC算法、CTF-GSC算法和本文算法进行语音增强实验。其实验仿真结果如表 2和表 3所示, 从表中可以看出, 当存在混响和偏角为0°时, 经TF-GSC算法增强后的语音信号的分段信噪比的增量比CTF-GSC算法高, 但是当偏角变化为15°时, 经CTF-GSC算法增强后的语音信号的分段信噪比的增量比TF-GSC算法要高。当输入分段信噪比越高, 混响时间越长时, CTF-GSC算法比TF-GSC算法的性能更好。但是在相同的实验条件下, 相比TF-GSC算法、CTF-GSC算法, 本文算法能进一步提高系统信噪比, 系统性能更稳定, 降噪效果更明显。
|
|
表 2 输出信号的分段信噪比测量结果对比(偏角0°) Tab. 2 Comparison of measurement results of segmented signal to noise ratio of output signal(0°) |
|
|
表 3 输出信号的分段信噪比测量结果对比(偏角15°) Tab. 3 Comparison of measurement results of segmented signal to noise ratio of output signal(15°) |
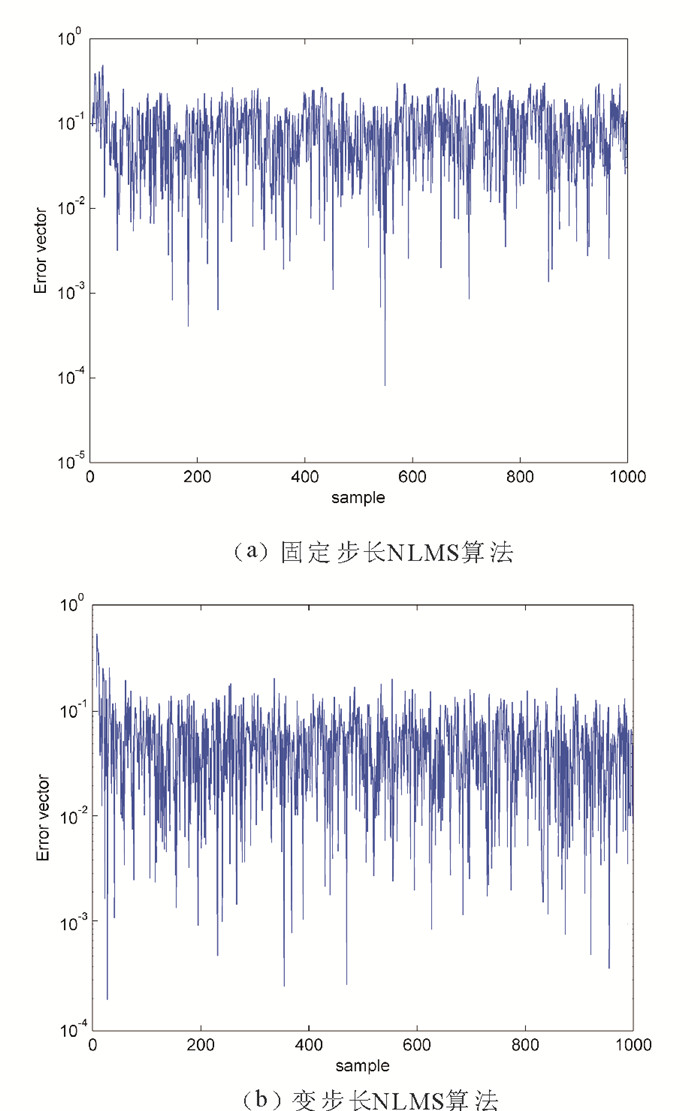
为了分析基本的固定步长NLMS算法和变步长NLMS算法的性能, 分别对这两种算法的误差权矢量和实际输出信号波动情况进行对比仿真, 在输入信号能量和信噪比相同的情况下, 利用基本的固定步长NLMS算法和本文所采用的变步长NLMS算法进行信号调制, 其各自的误差和信号波动情况的结果如图 4和图 5所示。
|
图 4 两种算法实际输出信号误差曲线 Fig. 4 The actual output signal error curve of the two algorithms |
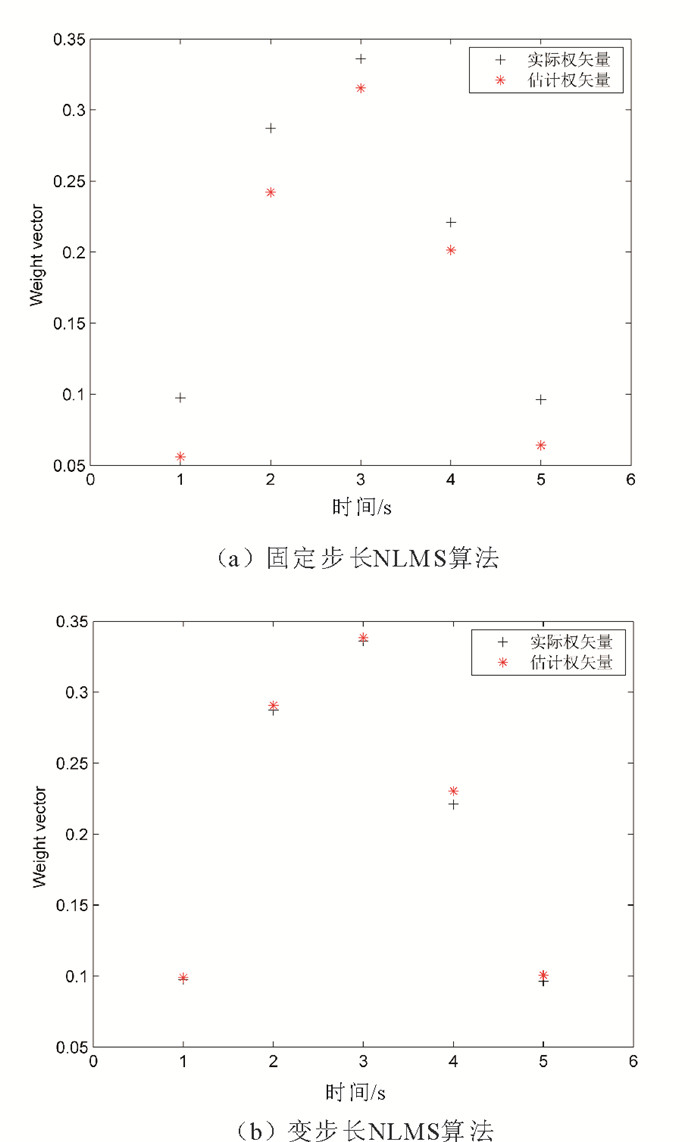
根据图 4和图 5可知, 基本的固定步长NLMS算法滤波器权重估计偏差较大, 相比而言, 本文所改进的变步长NLMS算法在减小信号误差方面有一定的改进, 其收敛速度也有一些改善, 变步长的NLMS算法可以实现噪声和权重的更好估计, 同时也提高了语音质量。
|
图 5 两种算法的实际权矢量与估计权矢量 Fig. 5 The actual weight vector and estimated vector of the two algorithms |
为进一步说明算法的性能, 将本文算法与文献[2]提出的TF-GSC算法,以及文献[3]提出的CTF-GSC算法进行了比较分析。
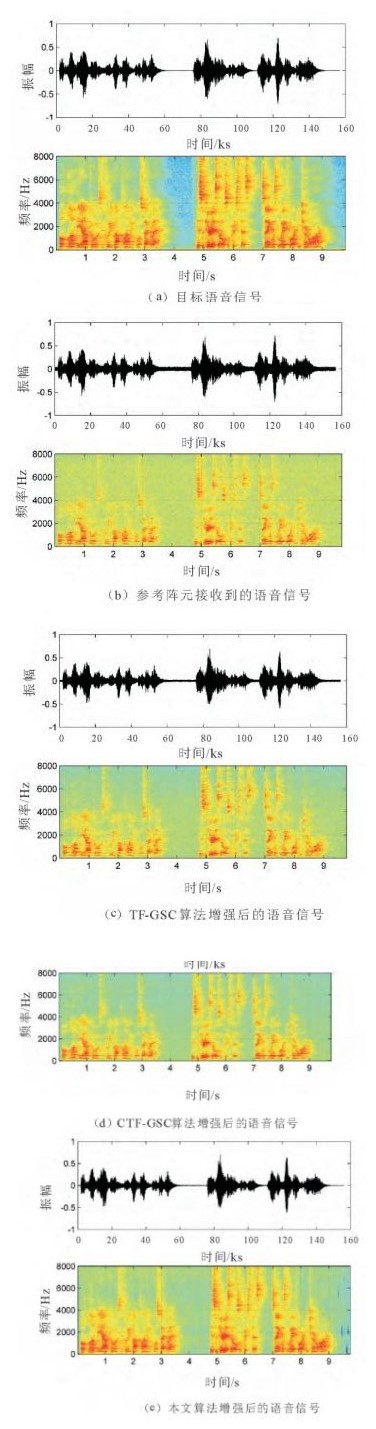
在含有相干性噪声和非相干性噪声的复杂环境下, 在输入语音信号的分段信噪比为5dB, 混响时间为0.94s, 目标声源与麦克风阵列的垂直方偏角为15°的实验条件下, 图 6(a)和图 6(b)分别为参考麦克风接收到的目标语音信号和参考阵元接收到的语音信号的时域波形图和语谱图。图 6(c)和图 6(d)分别为带噪语音信号经过TF-GSC和CTF-GSC算法增强后的语音信号的时域波形图和语谱图。从图 6中时域波形图的无语音段可以看出, CTF-GSC算法对于相干性噪声的抑制效果要优于TF-GSC算法, 但这两种算法都残留着一些非相干噪声, 并且在高频区域残留的非相干噪声更明显, 这表明两种算法对于非相干性噪声的抑制能力不强。图 6(e)为经过本文算法增强后的语音信号的时域波形图和语谱图, 从图中时域波形图的无语音段可以看出, 本文算法对相干性噪声的抑制效果要优于TF-GSC和CTF-GSC算法,同时也有效地抑制残留的非相干性噪声。由此可知, 在复杂混响的环境下, 相比其他算法, 本文算法对相干性噪声的抑制能力更好, 并且也能有效地抑制非相干性噪声, 降低语音失真。
|
图 6 信号处理前后的时域波形图和语谱图 Fig. 6 Time-domain waveforms and spectrograms before and after signal processing |
本文以麦克风阵列为例, 在基于变步长NLMS的CTF-GSC算法的基础上, 结合改进的后置滤波算法, 组成新的算法。改进的CTF-GSC算法对带噪语音信号进行语音增强, 更好地消除复杂环境中相干性噪声, 其中在CTF-GSC算法的自适应噪声消除模块采用变步长NLMS算法, 变步长NLMS算法具有好的收敛速度和低稳态误差, 增强了语音系统降噪能力。然后,再通过后置滤波算法, 在改进的后置维纳滤波算法中, 采用小波阈值多谱窗估计算法和VAD算法来改进基于先验信噪比的维纳滤波, 根据分段后验信噪比对噪声抑制因子进行分段取值, 更好地滤除残留的非相干性噪声。
实验结果表明:本文所提出的新算法对相干性噪声和非相干性噪声都有较好的抑制能力, 并且能有效地降低语音失真、提高系统信噪比、改善语音质量。改进算法的实验结果意味着CTF近似形式也可以有益地用于其他波束形成方法中, 并且也可以有效地联合后置滤波,相比于其他算法具有较明显的效果提升,尤其在混响的复杂环境中效果更明显。
| [1] |
GRIFFITHS L J, JIM C W. An alternative approach to linearly constrained adaptive beamforming[J]. IEEE Transactions on Antennas Propagat, 1982, 30(1): 27-34. DOI:10.1109/TAP.1982.1142739 |
| [2] |
GANNOT S, BURSHTEIN D, WEINSTEIN E. Signal enhancement using beamforming and nonstationarity with application to Speech[J]. IEEE Transactions on Signal Processing, 2001, 49(8): 1614-1626. DOI:10.1109/78.934132 |
| [3] |
TALMON R, COHEN I, GANNOT S. Convolutive transfer function generalized sidelobe canceler[J]. IEEE Transactions on Audio Speech and Language Processing, 2009, 17(4): 546-555. DOI:10.1109/TASL.2008.2009576 |
| [4] |
TALMON R, COHEN I, GANNOT S. Multichannel speech enhancement using convolutive transfer function approximation in reverberant environments[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing.IEEE Computer Society, 2009: 3885-3888.
|
| [5] |
TALMON R, COHEN I, GANNOT S. Relative transfer function identification using convolutive transfer function approximation[J]. IEEE Transactions on Audio Speech and Language Processing, 2009, 17(4): 546-555. DOI:10.1109/TASL.2008.2009576 |
| [6] |
COHEN I.On speech enhancement under signal presence uncertainty[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing.IEEE, 2001: 661-664.
|
| [7] |
COHEN I. Noise spectrum estimation in adverse environments:Improved minima controlled recursive averahinging[J]. IEEE Transactions on Speech and Audio Processing, 2003, 11(5): 466-475. DOI:10.1109/TSA.2003.811544 |
| [8] |
COHEN I, BEDUGO B. Microphone array post-filtering for non-stationary noise suppression[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. IEEE, 2002: 901-904.
|
| [9] |
COHEN I, GANNOT S. Speech enhancement based on the general transfer function GSC and postfiltering[J]. IEEE Transactions on Speech and Audio Processing, 2004, 12(6): 561-571. DOI:10.1109/TSA.2004.834599 |
| [10] |
WANG X F, GUO Y M, FU Q, et al. Speech enhancement using multi-channel post-filtering with modified signal presence probability in reverberant environment[J]. Chinese Journal of Electronics, 2016, 25(3): 512-519. DOI:10.1049/cje.2016.05.017 |
| [11] |
ZHANG M, WU S H, GUO W X, et al.A microphone array dereverberation algorithm based on TF-GSC and postfiltering[C]//2016 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting.IEEE, 2016: 1-4.
|
| [12] |
HUANG H C, LEE J. A new variable step-size NLMS algorithm and its performance analysis[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 2055-2060. DOI:10.1109/TSP.2011.2181505 |
| [13] |
EL-FATTAH M A A, DESSOUKY M I, ABBAS A M, et al. Speech enhancement with an adaptive Wiener filter[J]. International Journal of Speech Technology, 2014, 17(1): 53-64. DOI:10.1007/s10772-013-9205-5 |
| [14] |
甄国良.基于维纳滤波的语音增强算法的研究[D].太原: 太原理工大学, 2010.
|
| [15] |
LI X F, HORAUD R, GIRIN L, el al.Voice activity detection based on statistical likelihood ratio with adaptive thresholding[C]//IEEE International Workshop on Acoustic Signal Enhancement.IEEE, 2016: 1-5.
|
| [16] |
张超.语音端点检测方法研究[D].大连: 大连理工大学, 2016.
|
| [17] |
HU Y, LOIZOU P C. Speech enhancement based on wavelet thresholding the multitaper spectrum[J]. IEEE Transactions on Speech and Audio Processing, 2004, 12(12): 59-67. |
| [18] |
WUNG J, MIYABE S, JUANG B H. Speech enhancement using minimum mean-square error estimation and a post-filter derived from vector quantization of clean speech[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing.IEEE, 2009: 4657-4660.
|
 2017, Vol. 47
2017, Vol. 47