P91钢是一种新型高铬马氏体耐热钢, 因其优越的高温力学性能及抗蠕变性能, 常被用于石油、化工以及能源动力等领域。在长期高温、高压的环境中, 金属构件极易发生蠕变, 而蠕变断裂则会导致金属构件突然失效, 甚至造成财产的重大损失以及人员的伤亡[1]。因此,为避免上述情况发生, 精准预测服役构件的蠕变寿命显得尤为重要。
目前,国内、外在高温部件蠕变寿命预测方面提出了多种蠕变寿命预测模型, 如:Larson-Miller参数法[2]、∈参数法[3]等。由于未考虑材料在蠕变过程中的损伤, 这些方法在预测蠕变寿命时偏差较大。由于金属材料在高温、高压条件下会出现明显的黏性流动现象, 导致内部出现微孔或微裂纹等蠕变损伤[4-7]。因此, 利用基于损伤力学的蠕变损伤模型来预测高温构件的寿命已经成为一种重要的研究手段。经典的K-R模型使用十分广泛, 但由于蠕变应变和损伤演化方程耦合形式的限制, K-R模型在实际应用中具有很大的局限性[8-9]。双曲正弦蠕变损伤模型(Sinh模型)以及Liu and Murakami蠕变损伤模型为了突破这种限制, 用新的函数形式来耦合蠕变和损伤方程并描述蠕变损伤行为, 在预测服役寿命时表现出更加准确的特点[10-14]。
本文以国产P91钢作为研究对象, 首先对P91钢标准试样进行高温拉伸试验和单轴蠕变持久试验, 得到蠕变曲线及相关力学性能参数。利用试验数据拟合出K-R模型、Sinh模型和Liu and Murakami蠕变模型的模型参数并对其优化, 模拟得到P91钢的损伤演化过程、蠕变寿命以及蠕变率曲线。通过比较3种损伤模型在不同温度、应力条件下的预测精度, 从而为给定温度、应力条件下服役构件寿命预测模型的选择提供可靠依据。
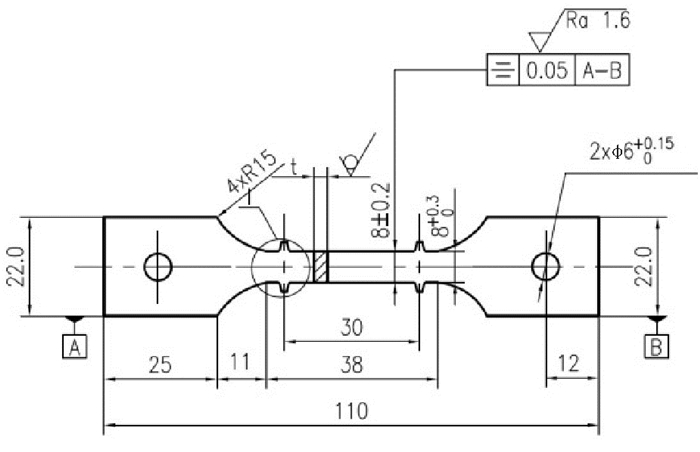
1 试验试验所用P91钢由天津大无缝钢管厂提供, 蠕变试样参照国家标准GB/T 2039-1997《金属拉伸蠕变及持久试验方法》, 试样标距尺寸为30mm×8mm×2mm, 如图 1所示。高温拉伸试验和蠕变持久试验在长春机械科学研究院研发的DDL300型万能试验机上进行, 得到P91钢在853K(180,190,200MPa),893K(135,145,155MPa)条件下的力学性能参数和单轴拉伸蠕变试验数据。通过数据拟合, 得到各温度下P91钢的蠕变损伤模型参数, 从而对P91钢的蠕变寿命和蠕变损伤行为进行模拟。
|
图 1 试样尺寸图 Fig. 1 Standard tensile sample |
在高温环境下, 材料组织容易发生劣化、机械性能降低, 导致蠕变应变快速增长。为了描述这种由微裂纹、孔洞等引起的材料劣化情况, Kachanov在传统Norton方程基础上引入损伤变量D, Rabotnov[9]将损伤变量与应力耦合, 形成Kachanov-Rabotnov方程, 表示如下:
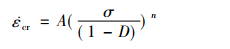
|
(1) |
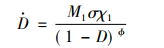
|
(2) |
式中: 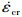
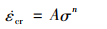
|
(3) |
由式(3)结合试验数据可确定Norton常数A,n。取初始时间t0=0, 初始损伤D0=0, 对式(2)进行积分, 得到损伤演化方程:
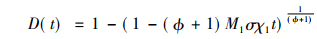
|
(4) |
将式(4)代入式(1), 整理并积分得到蠕变应变方程:
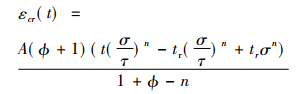
|
(5) |
式中: 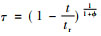
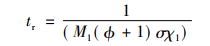
|
(6) |
常数M1可以通过上式由蠕变断裂数据计算。K-R模型参数如表 1所示。
|
|
表 1 P 91钢K-R模型材料常数 Tab. 1 K-R model material constant for P 91 |
双曲正弦损伤模型的蠕变率方程和蠕变损伤方程表示如下:
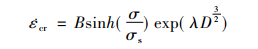
|
(7) |
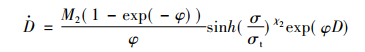
|
(8) |
式中:B和σs是第二阶段蠕变常数,M2,σt,χ2,φ,λ为双曲正弦模型常数。λ根据实验数据由λ= 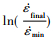
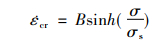
|
(9) |
由式(9)根据试验数据可确定第二阶段蠕变常数B和σs。对式(7)重新整理:
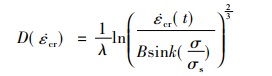
|
(10) |
对式(8)进行积分, 取初始时间t0=0,初始损伤D0=0,则
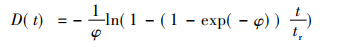
|
(11) |
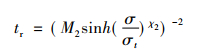
|
(12) |
M2,σt可以通过式(12)结合实验数据拟合得出。φ可以由式(10)和式(11)根据实验数据由拟合软件求的, P91钢Sinh模型材料常数如表 2所示。
|
|
表 2 P 91钢Sinh模型材料常数 Tab. 2 Sinh model material constant of P 91 |
单轴应力状态下的Liu and Murakami模型的蠕变率方程和蠕变损伤方程表述如下:
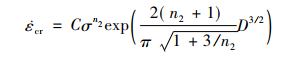
|
(13) |
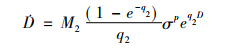
|
(14) |
式中:C,n2,M3,q2以及p均为Liu and Murakami模型常数。由于材料蠕变稳态阶段损伤变量D=0, 因此蠕变率方程可以简化为:
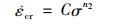
|
(15) |
根据试验数据由式(15)拟合材料常数C,n2。对式(13)进行积分, 取初值t0=0, D0=0:
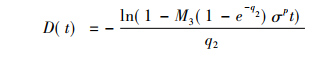
|
(16) |
当t=tr时D=1, 得到模拟蠕变寿命:
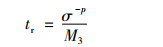
|
(17) |
根据单轴蠕变断裂数据, 材料常数M3,p可由式(17)拟合得出。将式(16)代入式(13), 可得蠕变应变率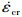
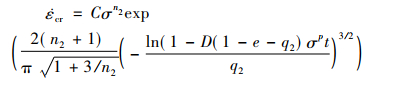
|
(18) |
通过式(18)确定各个应力水平下最合适的q2值。P91钢Liu and Murakami模型材料常数如表 3所示。
|
|
表 3 P91钢Liu and Murakami模型材料常数 Tab. 3 Liu and Murakami model material constant of P91 |
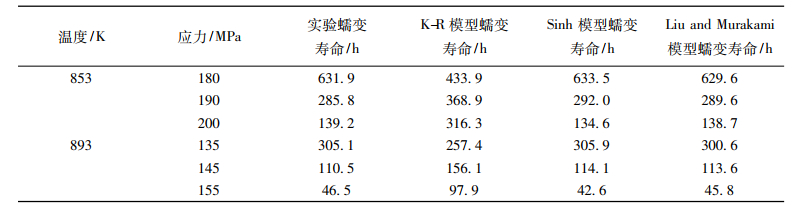
将K-R模型、Sinh模型以及Liu and Murakami模型的模拟蠕变断裂时间与试验断裂数据比较,得出3种模型在不同温度应力条件下对P91钢的蠕变寿命预测情况,如下表 4所示。
|
|
表 4 P91钢的模型蠕变寿命预测 Tab. 4 Predicted rupture life for models of P91 |
将Sinh模型、K-R模型以及Liu and Murakami模型寿命预测的累积误差计算如下表 5所示。
|
|
表 5 P91钢蠕变寿命预测累积误差 Tab. 5 Cumulative error of predicted rupture life of P91 for models |
可以看出:Sinh模型和Liu and Murakami模型对P91钢在853K,893K下预测的蠕变断裂时间与试验结果吻合程度较高, 且Liu and Murakami模型略优于Sinh模型。K-R模型在各温度应力条件下预测的断裂时间均与试验值相差较大。
可以看出:在各温度下Sinh模型和Liu and Murakami模型的累计误差远小于K-R模型, 在853K的条件下, Liu and Murakami模型的累积误差要略小于Sinh模型。因此, Sinh模型和Liu and Murakami模型的寿命预测能力较强, 且Liu and Murakami模型的蠕变寿命预测精度较Sinh模型稍高, K-R模型的寿命预测能力较差。
3.2 蠕变损伤由式(4),(11),(17), 分别可得K-R模型、Sinh模型以及Liu and Murakami模型模拟的蠕变损伤演化过程。由于不同温度和应力条件下的损伤过程相似, 以853K,180MPa下的情况为例, 比较3种模型的蠕变损伤过程, 归一化后的模拟蠕变损伤如图 2所示。
|
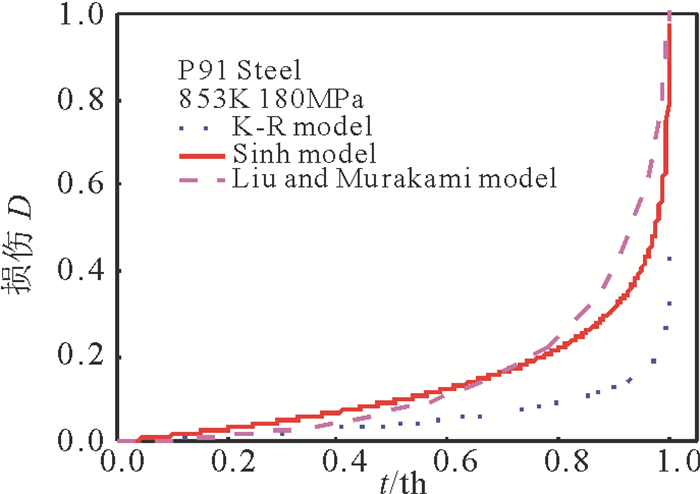
图 2 853K 180MPa条件下P91钢的蠕变损伤模拟曲线 Fig. 2 Creep damage simulating curves of P91 at 853K under 180MPa |
可以看出:在853K,180MPa下K-R蠕变模型的损伤在断裂时损伤变量没有达到1, 损伤基本在0.4~0.6之间, 而Sinh模型和Liu and Murakami模型的损伤演化是从0到断裂时达到1的过程。在实际应用过程中, K-R模型的损伤模拟结果与假定不符, 而Sinh模型和Liu and Murakami模型均能克服K-R模型的这种限制, 与实际情况相符合。
3.3 蠕变率曲线将P91钢在不同温度应力条件下的K-R模型和Sinh模型及Liu and Murakami模型的模拟蠕变率与试验数据比较, 结果如图 3所示。
|
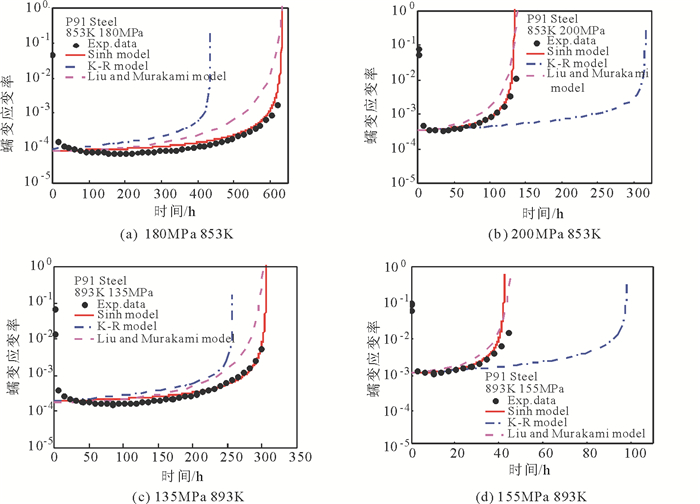
图 3 不同温度和应力水平下P91钢蠕变模拟曲线与试验曲线比较 Fig. 3 Comparison among creep model simulating curves of P91 steel and the experimental data |
可以看出:模拟蠕变曲线包含了稳态蠕变阶段和加速蠕变阶段, 3种模型都能够很好地对P91钢在该条件下的蠕变演化机制进行描述。在本文的温度应力下, Sinh模型和Liu and Murakami模型的蠕变率曲线与试验曲线吻合度较高, 且Sinh模型的模拟蠕变率曲线均更贴近于试验曲线。故而,在模拟实际蠕变过程时, Sinh模型更能真实反映蠕变率的变化过程, Liu and Murakami模型次之, 而K-R模型在模拟过程中与试验结果相差较大。
4 结论本文利用P91钢在853K(180,190,200MPa),893K(135,145,155MPa)条件下的单轴拉伸蠕变试验数据, 通过Sinh模型、Liu and Murakami模型和K-R模型对P91钢的蠕变寿命和蠕变损伤行为进行模拟。
1) 由3种模型的模拟损伤过程可得, K-R模型的损伤模拟结果与假定不符, 断裂时损伤变量不能达到1, 而Sinh模型和Liu and Murakami模型均能克服K-R模型的这种限制, 与实际情况相符合。
2) 在本文条件下对P91钢的蠕变曲线及蠕变寿命进行评估和预测时, 与实验数据相比Sinh模型预测能力最高, Liu and Murakami模型次之, K-R模型预测能力最差。本文基于P91钢所得结论对高铬耐热钢具有一定借鉴作用。
| [1] |
赵彩丽, 刘新宝, 郝巧娥, 等. 高温金属构件蠕变寿命预测的研究进展[J]. 材料导报, 2014, 28(23): 55-59. |
| [2] |
CAN B J. Remaining creep life estimation by strain assessment on plant[J]. International Journal of Pressure Vessels and Piping, 1982, 10(1): 11-30. DOI:10.1016/0308-0161(82)90023-0 |
| [3] |
EVANS R W, WILSHIRE B. Creep of metals and alloys[M]. London: The Institute of Metals, 1985.
|
| [4] |
涂善东. 高温结构完整性原理[M]. 北京: 科学出版社, 2003.
|
| [5] |
束国刚, 赵彦芬, 薛飞, 等. P91钢损伤试验研究与数值模拟[J]. 中国电机工程学报, 2010, 23: 103-107. |
| [6] |
李濒. 损伤力学基础[M]. 济南: 山东科学技术出版社, 1992.
|
| [7] |
荆建平, 孙毅. 高温蠕变分析的非线性连续损伤力学模型[J]. 推进技术, 2001, 22(2): 139-142. DOI:10.3321/j.issn:1001-4055.2001.02.015 |
| [8] |
KACHANOV L M. Rupture time under creep conditions[J]. International Journal of Fracture, 1999, 97(1-4): 11-18. |
| [9] |
RABOTNOV Y N, LECKIE F A, PRAGER W. Creep problems in structural members[J]. Journal of Applied Mechanics, 1970, 37(1): 249-260. |
| [10] |
STEWART C M.A hybrid constitutive model for creep, fatigue, and creep-fatigue damage[D].Orlando: University of Central Florida, 2013.
|
| [11] |
Haque M S, Stewart C M. Comparison of a new Sin-Hyperbolic creep damage constitutive model with the classic Kachanov-Rabotnov model using theoretical and numerical analysis[M]. Berlin: TMS 2015 144th Annual Meeting & Exhibition. Springer International Publishing, 2015: 937-945.
|
| [12] |
STEWART C M. Tertiary creep damage modeling of a transversely isotropic Ni-based superalloy [D].Orlando: University of Central Florida, 2009. https://www.researchgate.net/publication/47714781_TERTIARY_CREEP_DAMAGE_MODELING_OF_A_TRANSVERSELY_ISOTROPIC_NI-BASED_SUPERALLOY
|
| [13] |
HYDE C J, HYDE T H, SUN W, et al. Damage medchanics based predictions of creep crack growth in 316 stainless steel[J]. Engineering Fracture Mechanics, 2010, 77: 2385-2402. |
| [14] |
LIU Y, MURAKAMI S. Damage localization of conventional creep damage models and proposition of a new model for creep damage analysis[J]. JSME Int J, 1998, 41: 57-65. |
 2017, Vol. 47
2017, Vol. 47