2. 黄冈师范学院 旅游文化与地理科学学院, 湖北 黄冈 438000;
3. 长安大学 公路学院, 陕西 西安 710064;
4. 内江师范学院 地理与资源科学学院,四川内江 641000
2. School of Tourism and Geographic Sciences, Huanggang Normal College, Huanggang 438000, China;
3. School of Highway, Chang′an University, Xi′an 710064, China;
4. School of Geography and Resources Science, Neijang Normal University, Neijang 641000, China
随着改革开放政策的进一步深入和现代化建设的快速发展, 中国正在经历世界历史上规模最大、速度最快的城市化和机动化进程, 由于城市经济的飞速发展, 城市规模的不断扩大, 导致城市公交系统日趋复杂, 城市交通问题也日益加剧。因此研究和评估城市公交线路发展水平不仅能够明确城市公交线路优劣, 指导城市公共交通发展, 还有助于从本质上认识和解决城市交通拥堵、交通功能混乱等一系列问题。
在国外, 注重城市交通与社会发展的研究, 同时由于ITS(Intelligent transportation systems, 智能交通系统)的大规模投入使用, 使得城市公共交通智能化、可持续化、人文化以及交通服务能力和交通关系等成为研究热点[1-4]; 与国外相比, 中国在城市公共交通方面的研究还比较滞后, 目前的研究主要集中在公共交通通达性及其与城市社会经济发展的关系、公共交通发展水平的模拟评价和公共交通线路模型优化等三个方面, 集中在城市经济学、城市规划学和交通信息学等研究领域[5-7]。如詹璇等[8]从银行网点与公共交通的网络中心性及其在空间分布上的耦合性方面探讨了武汉市公共交通的发展特性; 黄晓燕等[9]以海南省为例定量分析了区域交通优势度与城市经济发展的关系; 李乐乐等[10]利用GIS分析技术选取综合评价指标分析了西安市城市道路网络的通达性现状, 为城市公共交通网络布局优化做出一定指导; 马雪莹等[11]采用熵权TOPSIS模型对重庆市石柱县交通线路通达性进行客观分析, 发现区域交通通达性与区域经济发展水平及土地流转面积具有高度趋同性。从研究对象方面来看, 不同研究者选取了不同尺度的研究对象, 季珏等[12]以北京市城八区为研究对象, 建立以市民出行满意度为目标的评价体系, 探讨城市空间结构与公共交通发展的关系; 吴瑶等[13]采用模型对西安、咸阳和宝鸡3个城市的常规公共交通进行适应性评价, 论证了其建立模型的可靠性和适用性; 郭丽娟等[14]则是以四川盆地城市群内18个城市为研究区建立最短时间距离模型和综合通达性模型分析城市交通通达性等。从研究方法上看, 主要是以建构模型和数理分析方法为主导的定量与定性相结合的研究, 如季珏等[15]以北京市城六区为研究对象采用数据包络分析法探讨了城市交通综合效率的评价方法; 聂伟等[16]提出了基于DEA和灰色关联分析的区域公路网综合评价方法, 并对我国15个省、自治区直辖市的公路网进行了综合评价; 胡启洲等[17]采用经济转化系数将多目标公交线网优化问题转为单目标优化问题并利用粒子群算法定量分析求解找出最佳公交线路; 孙志田等[18]提出采用改进的遗传算法公交线网优化模型并进行仿真研究, 提高了算法模型在公交线路网优化中的运行效率; 陈翔等[19]基于改进的临界簇模型对北京市地面公交线网可达性进行定量评价, 提出通过计算公共交通线路容量需求来评价地面公交线网可达性的方法, 具有较高实用性。
上述研究推动了城市公共交通领域的研究进展, 为后续的研究者提供了一定的理论基础和研究思路, 但主要针对大城市公共交通发展, 由于城市等级不同会导致交通发展的现状和方向存在差异, 且我国中小城市公共交通仍以公交为主, 所以在前人研究成果的基础上, 本文采用熵权TOPSIS法从3个方面构建评价指标体系, 对湖北省黄冈市黄州区2015年10~11月调查统计的16条公交线路的发展水平进行综合评价, 为客观定量评价黄冈市公交线路发展现状和指导中小城市公交路线建设提供一定可行参考。
1 研究区概况与数据来源 1.1 研究区概况黄州区系属湖北省黄冈市, 是黄冈市政治、经济、文化中心。全区现辖禹王街道、南湖街道、东湖街道、赤壁街道、路口镇、陈策楼镇、堵城镇和陶店乡, 因位于武汉市半小时经济圈以内的天然地理优势, 黄州区在武汉“1+8”城市圈发展计划中占用重要战略地位, 评价黄州区交通各方面发展水平对于黄冈市未来交通建设和城市发展都具有重要意义。黄州区应抓住武汉“1+8”城市圈建设发展机遇, 既要加强对外交通建设, 也应当完善内部公交发展, 做到内外同步, 共同拉动黄冈市交通发展。
1.2 数据来源1) 基础数据。研究所用黄州区地理位置、行政区划图等面数据来源于国家基础地理数据库, 公交线路、交通线路等线数据, 公交站点等点数据均来自Google Earth影像数据和ArcGIS 10.4数字化所得。
2) 统计数据。城市公交发展水平评价指标主要参考同类型研究中所用指标和实际调查所获取指标, 具体评价指标的原始数据来源于2015年10~11月黄冈师范学院旅游文化与地理科学学院公交跟车调查统计数据, 其中公交线路长度、站点间距等数据来源于Google Earth影像数据矢量化所得。
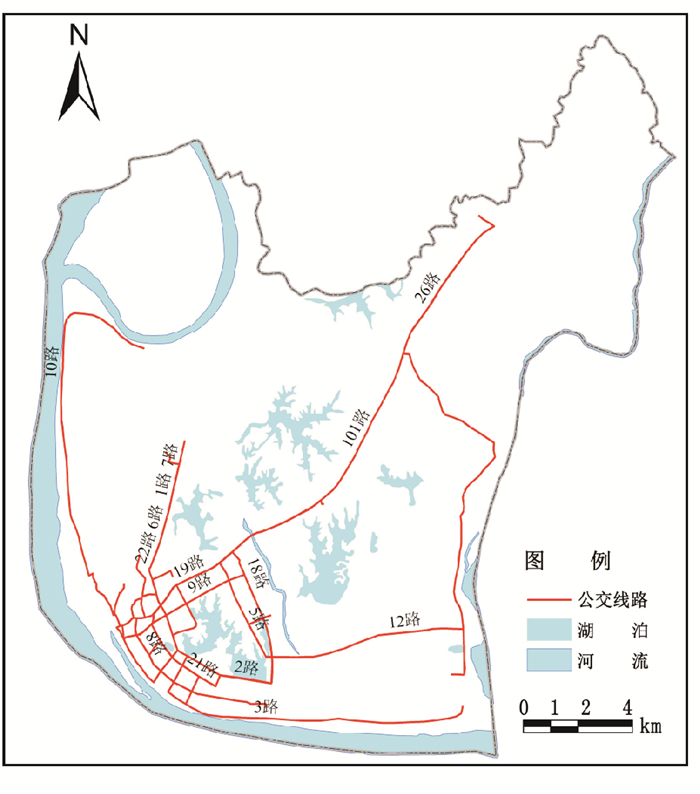
|
图 1 黄州区公交线路分布图 Fig. 1 The distribution of bus lines in Huangzhou District |
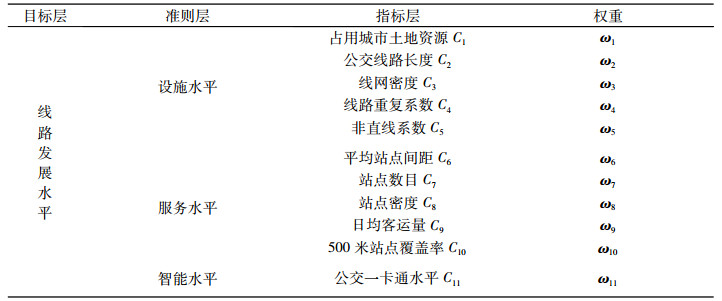
公交线路发展水平是城市公交设施水平、服务水平和智能水平等多方面的综合体现,其综合评价对公交体系的智能建设、城市的可持续发展具有重要意义。考虑到影响城市公交线路发展水平因素的多元性、综合性和复杂性, 在建立指标体系时严格遵循系统性、科学性和可操作性等评价原则, 并参考杨晓光和刘铮等[20-21]的城市公共交通发展评价指标体系从设施水平、服务水平和智能水平3个层次共11个指标对城市公交线路发展水平进行综合评价。
2.2 评价指标权重的确定方法——熵权法“熵”是热力学中用于表征物质能量退化状态的一种参量, 随着其在信息论等领域的不断引入使用和发展成熟, 目前在社会经济研究和工程技术研发领域亦表现出良好应用发展前景[22]。采用熵权法来确定指标权重, 实质是根据各个评价指标变异性的大小来客观确定其在评价体系中的重要程度, 与主观赋予权重相比, 熵权法确定权重不仅能客观真实地反映出城市公交线路发展水平评价体系中各个指标的地位和作用、减小数据分析中的人为主观误差, 还可以反映数据隐含的相关信息, 增强评价指标的差异性和分辨率[23]。其详细计算步骤如下:
1) 构建判断矩阵
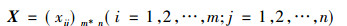
|
(1) |
式中xij为城市公交发展水平评价指标; m为待评价的公交线路数, n为每条待评价线路的评价指标数。
2) 判断矩阵标准化处理
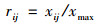
|
(2) |
式中rij为评价指标xij进行标准化处理后的规范值, xmax为同一类型评价指标中的最大统计值。
3) 评价指标熵值的计算
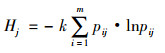
|
(3) |
式中Hj为第j个评价指标的熵值,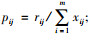
4) 计算评价指标的权重
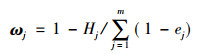
|
(4) |
式中ωj为第j个评价指标的权重, 即第j个评价指标的熵权, ωj∈[0, 1],且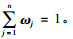
TOPSIS法是由C.L.Hwang和K.Yoon在1981年首次提出的用于解决多目标决策分析的一种有效方法, 其实质是通过判断评价对象与最优解、最劣解之间的距离来进行优劣排序, 选择出距离最优解最近, 同时又距离最劣解最远的方案[24-25]。熵权TOPSIS与传统的依靠专家主观决策确权的TOPSIS相比较而言, 在评价结果的客观性和可信度上更具优势。基于熵权法改进传统TOPSIS算法并建立模型来实施对城市各公交线路发展水平的评价。详细步骤如下:
1) 计算加权评价矩阵
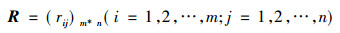
|
(5) |
式中rij=ω·xij。
2) 确定最优解与最劣解
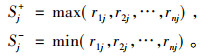
|
(6) |
3) 计算各线路方案与最优解和最劣解的欧式距离
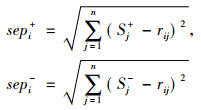
|
(7) |
4) 计算综合评价指数

|
(8) |
式中Ci∈[0, 1], Ci的值越大说明评价对象发展水平越高。
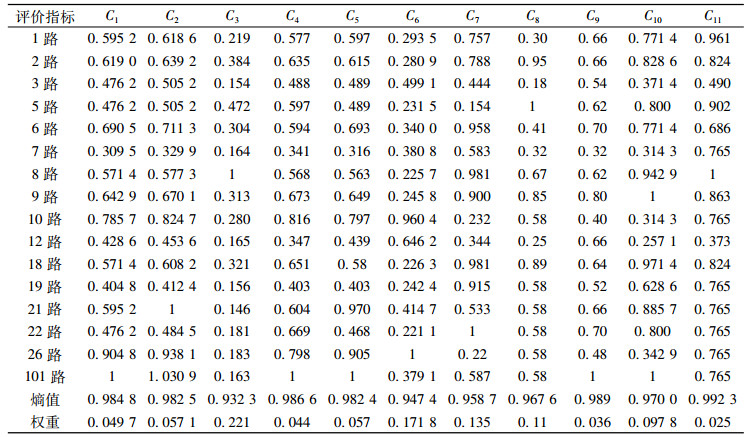
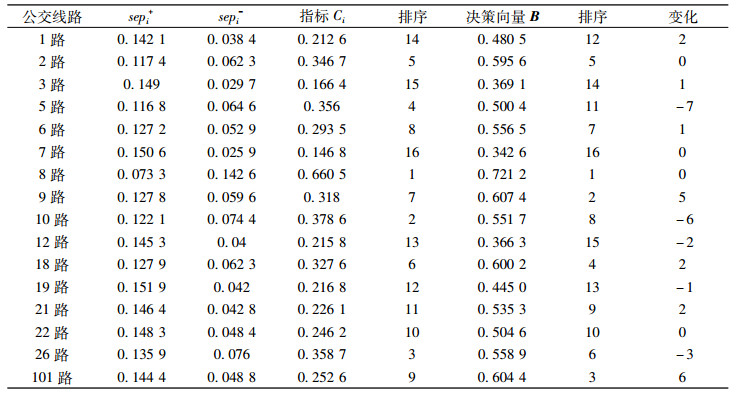
3 结果与分析 3.1 黄州区公交线路发展水平研究结果根据表 1所建立的评价指标体系构建黄州区公共交通线路发展水平判断矩阵, 根据公式(1)~(4)依次计算出评价公交发展水平的11个指标的规范值、熵值和权重, 结果如表 2所示, 再根据公式(5)~(8)依次计算出黄冈市区16条公交线路的评价指标值分别与最优解、最劣解的欧式距离从而得出其与最优解的贴近程度值(Ci), 根据贴近程度值的大小依次排序得到公交线路发展水平排名, 为了验证评价结果的可信度, 采用模糊数学法进行再次分析, 其过程如下:由熵权法所得各个评价指标的权重构建权重向量ωj, 根据公式B=(rij·ωj)求得模糊综合评价结果B=(0.480 5, 0.595 6, 0.369 1, 0.500 4, 0.556 5, 0.342 6, 0.721 2, 0.607 4, 0.551 7, 0.366 3, 0.600 2, 0.445 0, 0.535 3, 0.504 6, 0.558 9, 0.604 5), 将得出的结果与熵权TOPSIS模型分析结果进行比较, 结果如表 3所示。
|
|
表 1 城市公交线路发展水平评价指标体系 Tab. 1 The indicator system of bus lines development level in a city |
|
|
表 2 各评价指标规范化矩阵、熵值及权重 Tab. 2 The weight of standardization of decision matrix, entropy and weight of assess index |
|
|
表 3 黄州区各公交线路综合评价结果 Tab. 3 The results of comprehensive evaluation of bus lines in Huangzhou District |
由表 2可知, 熵值与指标权重存在显著负相关性, 在11个评价指标中, 公交线网密度所占权重最大, 为0.221;其次公交线路平均站点间距和站点数目所占权重也较大, 分别为0.171 8、0.135;而公交一卡通水平评价指标、线路重复系数和日均客运量等评价指标所占权重则较小, 分别是0.025,0.044和0.056。从表 2中各个指标权重的高低可以看出公交线网密度直接影响到公交线路发展水平, 公交线网密度是指单位城市用地面积上所拥有的公交线路的长度, 单位是km/km2, 作为公交线路发展水平评价中最基本的设施水平评价指标, 其值大小在一定程度上反映了城市公交线路的通车里程数和公交通达度水平; 公交线路平均站点间距和站点数目在很大程度上反映了公交线路的便捷度和服务水平, 其在评价体系中均占有较高权重, 这与现实公交线路评价中的服务最大化和便民原则是一致的。公交一卡通水平作为城市公交线路发展水平综合评价中的智能化水平在评价体系中所占权重较低, 原因可能是由于黄州区公交公司近年来对于公交一卡通使用的大力推进和优惠政策的实施以及调查数据中对于智能化水平评价指标的采集有限, 导致各条线路公交一卡通使用水平相差不大, 使得该指标变异程度较低, 在整个评价体系中所占权重最低。总地来说, 在公交线路发展水平综合评价中, 设施水平权重>服务水平权重>智能水平权重, 指标权重的排序基本符合中小城市公共交通发展现状。因此, 黄州区未来公交发展应当在保障公交线路基础设施水平的基础上, 大力提高服务水平和智能水平。
在表 1建立的评价指标体系下, 根据表 3中采用熵权TOPSIS模型求解出的16条公交线路综合排名可知, 黄州区公交线路发展水平参差不齐, 优劣差距较大, 其中以8路、2路、18路、9路等为主排名相对靠前, 公交发展整体水平高于其他线路; 而以1路、3路、12路、19路等为代表的其他几路公交线路排名靠后, 公交线路发展水平明显较其他线路差。可以发现, 在黄州区内部, 公交发展存在明显差异。城市公交线路发展水平的高低有其遵循的一定评价标准, 即公交线路的发展是否适应城市交通需要以及适应程度的高低, 本文采用的标准如表 4所示[13], 按照城市公交线路发展水平评价标准来评价黄州区16条公交线路发展水平, 如表 4所示:黄州区16条公交线路中处于高水平的公交线路为0条; 处于较高水平的公交线路仅1条, 即8路公交线; 处于适中水平的公交线路为0条; 除去3,7路线路属于极低水平, 其余13条公交线路均处于低水平。总体来说, 黄州区公交线路发展处于偏低水平, 且与大中城市或规范公交发展标准存在较大差距。黄冈市位于湖北省东部, 大别山南麓, 长江中游北岸, 下辖区多为欠发达革命老区及贫困县, 黄州区地形虽已平原为主, 但区内河湖水网纵横交错、地块分散, 由于地理地形特征、历史原因等使得黄州区公交线路发展受到很大限制, 而公交线路布设缺乏规划, 公交经营垄断等也是其公交线路发展水平低下的原因。从表 3可以看出, 利用模糊数学分析方法得到的结果与熵权TOPSIS模型所得结果大致吻合, 结果变化不大, 少数线路排名的波动可能是由于两种不同算法的计算过程及其各自的评价倾向性差异导致, 研究说明熵权TOPSIS模型在城市公交线路发展水平评价中具有较高的可行性。
|
|
表 4 黄州区公交线路发展水平评价标准及结果 Tab. 4 The evaluated standard and results of the adaptability of bus lines in Huangzhou District |
1) 采用熵权TOPSIS构建模型对公交线路发展水平进行综合评价较为客观合理。首先, 熵权法计算权重排除了人为确定权重的主观误差影响, 其次, 被广泛应用于地学统计中的TOPSIS分析模型有其可靠的数学基础和严谨的推算步骤。因此将熵权法和TOPSIS分析模型相结合来分析公共交通线路发展水平也具有高度的客观性和可行性。采用模糊数学法检验熵权TOPSIS模型, 所得结果具有较好的吻合性, 表明熵权TOPSIS模型适合公交线路发展水平综合评价, 具有较高的可行性和可重复性, 对于中小城市公交线路评价和发展具有较高借鉴意义。在今后的城市公交发展研究中, 由于数据丰度、精度的提高和指标的更新变化, 公交线路发展水平评价体系和评价方法将会更加完善。
2) 黄州区公交线路发展整体处于偏低水平, 公交线路绝大多数发展水平偏低, 未来公交事业发展应主要集中在提高服务水平和智能水平上。在物联网、互联网+、大数据等已逐步发展渗透走向成熟的21世纪新阶段, 现代城市正逐步向智慧城市转型, 城市公交也正迈向智能公交发展阶段, 因此相关研究工作也应不断更新和发展, 顺应甚至引导城市公交的科学发展。
| [1] |
CHENG X, YANG L, SHEN X. D2D for intelligent transportation systems: A feasibility study[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 1784-1793. DOI:10.1109/TITS.2014.2377074 |
| [2] |
CRAINIC T G, GENDREAU M, POTVIN J Y. Intelligent freight-transportation systems: Assessment and the contribution of operations research[J]. Transportation Research Part C Emerging Technologies, 2009, 17(6): 541-557. DOI:10.1016/j.trc.2008.07.002 |
| [3] |
ONG G P, SINHA K C, FWA T F. Strategies for achieving sustainability through integrated transportation and urban development in the USA and Asia[J]. Asian Transport Studies, 2010, 1: 89-104. |
| [4] |
TOMS K, SONG W. Spatial analysis of the relationship between levels of service provided by public transit and areas of high demand in Jefferson county, Kentucky[J]. Papers in Applied Geography, 2016, 2(2): 147-159. DOI:10.1080/23754931.2015.1115365 |
| [5] |
程钰, 刘雷, 任建兰, 等. 县域综合交通可达性与经济发展水平测度及空间格局研究——对山东省91个县域的定量分析[J]. 地理科学, 2013, 33(9): 1058-1065. |
| [6] |
李煜华, 胡运权. 灰色聚类法在城市公共交通发展水平评价中的应用[J]. 数学的实践与认识, 2006, 36(2): 125-132. DOI:10.3969/j.issn.1000-0984.2006.02.022 |
| [7] |
陈丹, 徐文远. 基于遗传算法的轨道交通与常规公交线路优化方案[J]. 西北大学学报(自然科学版), 2016, 46(3): 364-370. |
| [8] |
詹璇, 林爱文, 孙铖, 等. 武汉市公共交通网络中心性及其与银行网点的空间耦合性研究[J]. 地理科学进展, 2016, 35(9): 1155-1166. |
| [9] |
黄晓燕, 曹小曙, 李涛. 海南省区域交通优势度与经济发展关系[J]. 地理研究, 2011, 30(6): 985-999. |
| [10] |
李乐乐, 白建军, 宋冰洁. 西安市交通网络综合通达性研究[J]. 人文地理, 2014, 29(5): 88-93. |
| [11] |
马雪莹, 邵景安, 徐新良. 基于熵权-TOPSIS的山区乡镇通达性研究——以重庆市石柱县为例[J]. 地理科学进展, 2016, 35(9): 1144-1154. |
| [12] |
季珏, 高晓路. 北京城区公共交通满意度模型与空间结构评价[J]. 地理学报, 2009, 64(12): 1477-1487. |
| [13] |
吴瑶, 陆建, 邱红桐, 等. 基于TOPSIS模型城市常规公共交通适应性评价[J]. 交通信息与安全, 2014, 32(6): 153-158+165. DOI:10.3963/j.issn.1674-4861.2014.06.025 |
| [14] |
郭丽娟, 王如渊. 四川盆地城市群主要城市通达性及空间联系强度研究[J]. 人文地理, 2009, 24(3): 42-48. DOI:10.3969/j.issn.1003-2398.2009.03.009 |
| [15] |
季珏, 高晓路, 刘星辰. 城市交通效率的多目标评价方法研究——以北京市城六区为例[J]. 地理科学进展, 2016, 35(1): 118-125. |
| [16] |
聂伟, 邵春福, 杨励雅, 等. 基于DEA和灰色关联分析的区域公路网综合评价方法[J]. 交通运输系统工程与信息, 2007, 7(4): 96-100. DOI:10.3969/j.issn.1009-6744.2007.04.015 |
| [17] |
胡启洲, 邓卫, 周媛. 基于定量分析的公交线路网络优化与粒子群算法[J]. 公路交通科技, 2007, 24(10): 129-132. DOI:10.3969/j.issn.1002-0268.2007.10.028 |
| [18] |
孙志田, 张建梅, 闫常丽. 基于遗传算法公交线路网优化模型仿真研究[J]. 计算机仿真, 2011, 28(11): 335-338. DOI:10.3969/j.issn.1006-9348.2011.11.081 |
| [19] |
陈翔, 李强, 王运静, 等. 临界簇模型及其在地面公交线网可达性评价中的应用[J]. 地理学报, 2009, 64(6): 693-700. DOI:10.3321/j.issn:0375-5444.2009.06.006 |
| [20] |
杨晓光, 安健, 刘好德, 等. 公交运行服务质量评价指标体系探讨[J]. 交通运输系统工程与信息, 2010, 10(4): 13-21. DOI:10.3969/j.issn.1009-6744.2010.04.002 |
| [21] |
刘铮, 余一村, 程申. 基于熵权物元模型的公交综合评价指标体系[J]. 城市交通, 2010, 8(6): 79-84. DOI:10.3969/j.issn.1672-5328.2010.06.013 |
| [22] |
张力, 刘雪阳, 洪俊, 等. 基于熵的数字化人机交互复杂度研究[J]. 中国安全科学学报, 2015, 25(10): 65-69. |
| [23] |
杜挺, 谢贤健, 梁海艳, 等. 基于熵权TOPSIS和GIS的重庆市县域经济综合评价及空间分析[J]. 经济地理, 2014, 34(6): 40-47. |
| [24] |
李灿, 张凤荣, 朱泰峰, 等. 基于熵权TOPSIS模型的土地利用绩效评价及关联分析[J]. 农业工程学报, 2013, 29(5): 217-227. |
| [25] |
徐晗. TOPSIS模型的改进算法在农业干旱脆弱性评价中的应用——以陕西省关中地区为例[J]. 西北大学学报(自然科学版), 2016, 46(2): 277-281. |
 2017, Vol. 47
2017, Vol. 47
 , 杨煜岑1, 江砥2, 陈明3, 张彬4, 李新尧1
, 杨煜岑1, 江砥2, 陈明3, 张彬4, 李新尧1