网络数据流量的激增是目前入侵检测系统(Intrusion detection system, IDS)面临的主要挑战[1-2]。这类大规模的数据中往往包含了大量的重复、噪音或冗余的特征信息, 不仅影响检测的实时性, 也使得分类计算的复杂度大大增加, 降低分类的准确率。因此, 在处理这类数据集时,需要在数据预处理阶段消除不相关或冗余的特征, 选择出最优的特征子集, 即对数据进行特征选择[3-4], 然后将选择出的特征子集用于分类训练。所以, 特征选择是入侵检测的关键, 特征选择结果的好坏直接影响分类器的分类精度和效率。
针对入侵检测中的特征选择, 研究人员已经进行了许多研究。特征选择技术通常分为过滤式和封装式。过滤式主要是把信息度量、距离度量和一致性度量等作为评价特征之间相关性的准则, 且一个好的评价准则可以有效地获得最优特征子集; 封装式则需要一个预先设定的学习算法, 将特征子集在其算法上的表现作为评估,以确定最终的特征子集[5-6]。Amiri等[7]提出了一种改进的基于互信息的过滤式特征选择算法MMIFS, 该算法使用互信息方法进行前向序列特征选择,以度量特征间的相关性, 选出最优或次优特征子集, 然后,把这些特征集用于训练LSSVM分类器,以建立IDS。Ambusaidi等[8]提出了一种混合的特征选择算法HFSA, 该算法属于封装式方法, 通过初步搜索去除不相关或冗余特征,以减小在封装时从整个原数据集到候选子集的搜索范围, 然后,用分类算法LSSVM精简出前一阶段选出的候选集,以获得最优特征子集。但是,该封装式特征选择的计算成本较大, 效率也较低。
本文提出了一种新的基于互信息的过滤式特征选择算法(Novel mutual information based feature selection, NMIFS), 该算法通过互信息作为度量去评估特征和输出类之间的相关性, 保留最相关的候选特征子集, 然后将这些子集应用于分类器LSSVM训练以建立IDS。NMIFS算法能处理线性和非线性相关的数据, 并去除噪音、冗余或无关的特征,得出最优子集, 在提高分类器的分类精度和效率同时, 也能提高IDS的检测率。
1 基于互信息的特征选择互信息(Mutual information, MI)是变量相关估计中最重要的信息度量之一, MI常用来评价特征和目标属性的相关程度, 不用预先考虑数据的分布情况, 可以处理线性或者非线性关系的变量[9-10]。因此, 本文基于互信息提出一种特征选择算法, 旨在选择出一组特征子集, 该子集与类标签的相关性最大。设有两组连续的随机变量U={u1, u2, …, ud}和V={v1, v2, …, vd}, 其中d指样本的总数, U和V之间的互信息定义为
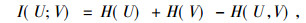
|
(1) |
H(U)和H(V)分别是U和V的信息熵。信息熵是指随机变量U和V的不确定度, 其中, H(U)=-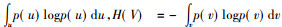
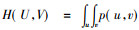
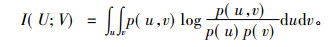
|
(2) |
其中, p(u, v)为联合概密度函数, p(u)=∫p(u, v)dv和p(v)=∫p(u, v)du是边际概率。而对于两个离散随机变量之间的互信息可以用一个联合概率质量函数p(u, v)和边际概率p(u)及p(v)表示为
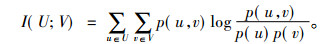
|
(3) |
如果特征包含关于类的重要信息, 那么这个特征对于类就是相关的, 反之该特征则为不相关的或者冗余的。换言之, 如果特征和类C之间有较高的互信息I(C; f), 则说明该特征对类C有较高的预测能力, 反之, 如果I(C; f)为0, 则说明特征f和类C相互独立, 特征f是冗余的, 将会降低分类效率和精度。由于MI值作为从数据源中选择特征的标准, 所以, 任何计算错误都会导致基于互信息的特征选择算法的准确率降低。而MI的计算需要从输入数据实例中估计概率密度函数和熵。
由于难以从输入数据实例中估计概率密度函数或熵,因此,有许多估计技术应用于MI的计算。目前, 直方图和核密度估计技术是估计概率密度函数最常用的估计方法[11]。直方图方法计算有效, 但只适用于低维数据空间,而核密度估计则面临高估计质量和高计算负载的问题。由于本文主要研究高维数据特征, 故这两种技术均不适用。为了避免上述问题, 文献[12]提出了一种基于K近邻的估计方法, 该方法先计算从基准面到其对应的K近邻的平均距离, 然后通过该距离估计所给数据的熵。该估计方法的优点在于可以估计任何数据空间的两个随机变量之间的MI值, 而且在p(u),p(v)和p(u, v)未知的情况下, 该算法也可以估计熵。
2 NMIFS算法 2.1 NMIFS算法描述本文基于MMIFS算法[7]进行改进, 在MMIFS算法中, 需要通过设置合适的自由参数β使特征选择算法得以实现, 如果选择不恰当将直接影响算法的性能, 因此, 本文提出了一种新的基于互信息的特征选择算法(NMIFS)。该算法去除了自由参数β,式(4)为特征选择准则的一个新的表示方法, 目的是从一个初始输入特征集中选择一个特征, 该能够在最大化互信息I(C; fi)的同时, 也能使冗余特征的平均值MR最小化。
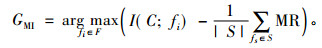
|
(4) |
其中, I(C; fi)为特征fi携带类C的信息量, S为特征子集,MR是特征fi对于特征fs的相对最小冗余特征,定义为
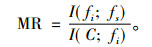
|
(5) |
其中,fi∈F, fs∈S。为了检验特征需要减少的数量, 设定GMI的阈值Th=0, 因此式(4)有以下3种情况:
1) 当GMI=0时, 当前特征fi对于输出C来说是不相关或不重要的, 因为fi在选入特征子集S之后, 不能为分类提供任何信息。因此, 当前候选特征fi将从S中移除。
2) 当GMI>0时, 当前特征fi对于输出C来说是相关或重要的, 因为在fi选入特征子集S之后, 该特征能为分类提供相关或重要的信息。当前候选特征fi将添加到S中。
3) 当GMI < 0时, 当前特征fi对于输出C来说是冗余的, 因为该特征会降低特征子集S和输出C之间互信息量。式(4)中第二部分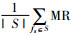
NMIFS算法特征选择过程的伪代码如下:
Input: Feature set F={fi, i=1, 2, …, n}
Output: S-the selected feature subset
Begin
Step 1. Initialization: set S=φ;
Step 2. Calculate I(C; fi) for each feature,
i=1, 2,…, n;
Step 3. nf=n; Select the feature fi such
that:
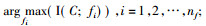
Then, set
F←F{fi}; S←S∪{fi};
nf=nf-1;
Step 4. while F≠φ do
Calculate GMI in (4) to find fi where
i∈{1, 2, …,nf};
nf=nf-1;
F←F{fi};
If(GMI>0) then
S←S∪{fi};
end
end
Step 5. Sort S according to the value of GMI of each selected feature
return S
2.2 NMIFS算法和LCFS算法为了证明NMIFS算法的高效性, 即较低的计算复杂度, 本文将NMIFS算法与LCFS算法(Linear correlation based feature selection)[13]进行性能对比。由于在LCFS算法中使用了线性相关系数(Linear correlation coefficient, LCC)作为评估两个随机变量相关性的度量, 尽管LCC衡量随机线性相关变量之间的相关性有着高效性和准确性, 但对于非线性相关变量并不敏感。因此用LCC代替算法1中的MI, 给出两个类型相同的随机变量U和V, 两个变量之间的相关系数定义如下:
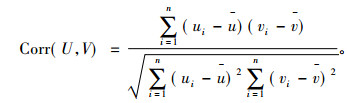
|
(6) |
Corr(U,V)的取值范围为[-1, 1], 当Corr(U,V)接近于-1或1时,表明两个变量间有较强的相关性, 若该值接近于0,则说明其相关性较弱。算法2为LCFS的具体过程, 主要通过式(7)进行特征选择, 最大化GCorr以消除无关和冗余特征。
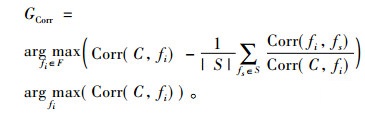
|
(7) |
LCFS算法的伪代码如下:
Input: Feature set F={fi, i=1, 2,…, n}
Output: S-the selected feature subset
Begin
Step 1. Initialization: set S=φ;
Step 2. Calculate Corr(C,fi) for each
feature, i=1, 2,…, n;
Step 3. nf=n; Select the feature fi such
that:
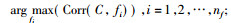
Then, set F←F{fi}; S←S∪{fi};
nf=nf-1;
Step 4. while F≠φ do
Calculate Corr(C,fi) in (7) to find
fi where i∈{1, 2, …nf};
nf=nf-1;
F←F{fi};
If(Corr(C,fi)>0) then
S←S∪{fi};
end
end
Step 5. Sort S according to the value of Corr(C,fi) of each selected feature
return S
对比以上两种算法,NMIFS算法中,式(5)计算的时间复杂度为O(n),式(4)计算的时间复杂度为O(logn),故算法NMIFS算法伪代码的时间复杂度T(n)=O(nlogn)。而在LCFS算法中,式(6)分子部分采用了最小二乘法,计算的时间复杂度为O(n),分母部分则是O(n2),则该式计算的时间复杂度为O(n2)。在式(7)中,当fi确定时,时间复杂度为O(logn),故LCFS算法伪代码的时间复杂度T(n)=O(n2logn)。由此可见,NMIFS算法相较于LCFS算法在效率上有所提升。
2.3 NMIFS算法的应用将NMIFS算法应用于入侵检测中可提高系统的检测性能和准确率。而建立入侵检测系统主要分为4个阶段:①数据收集, 主要是网络数据包序列的收集; ②数据预处理, 主要是训练和测试数据集的预处理和重要特征的选择; ③分类器训练, 本文用LSSVM算法对分类模型进行训练; ④攻击识别, 训练的分类器用于检测测试数据集的入侵行为。
在建立入侵检测系统时, 首先进行数据收集, 然后对数据进行预处理。在数据预处理的过程中, 本文用NMIFS算法进行特征选择, 但是该算法只能对特征的相关性进行排序, 不能得出需要训练分类器的特征的最佳数量。因此, 本文利用了文献[7]中相同的技术, 该技术首先用NMIFS算法对分类过程重要的所有特征进行排序, 然后将特征逐一添加到分类器中。一旦在训练过程中分类准确率达到最高, 最佳特征数量就最终得以决定。
选择出最优特征子集后, 将子集放入分类器进行训练, 本文采用最小二乘支持向量LSSVM[12]作为训练模型的算法, 与传统SVM算法相比, 该算法能降低计算复杂度[8]。本文使用了KDD CUP 99数据集, 需要从所有类中选择5个最优特征子集, 因此, 本文将用到5个LSSVM分类器。
完成上述步骤后, 通过已训练的分类器识别正常和入侵数据流量, 然后测试数据集直接指向已训练的模型中检测入侵行为, 记录匹配为正常类则视为正常数据, 反之, 则视为攻击数据。如果分类器模型确认该记录异常, 异常记录(攻击类型)的子类可以被确定为记录的类型。算法3和算法4描述了检测的过程。
以下是基于LSSVM的入侵检测的伪代码(在多类情况下, 从正常网络流量中识别入侵网络流量):
Input: LSSVM Normal Classifier, selected features(normal class), an observed data item x
Output: Lx-the classification label of x
Begin
Lx←classification label of x with LSSVM of Normal class
if Lx==“Normal” then
Return Lx
else
do: Run Algorithm 4 to determine the class of attack
end
end
以下是基于LSSVM的攻击分类的伪代码:
Input: LSSVM Normal Classifier, selected features(normal class), an observed data item x
Output: Lx-the classification label of x
begin
Lx←classification of x with LSSVM of DoS class
if Lx==“DoS” then
Return Lx
else
Lx←classification of x with LSSVM of Probe class
if Lx==“Probe” then
Return Lx
else
Lx←classification of x with LSSVM of R2L class
if Lx==“R2L” then
Return Lx
else
Lx==“U2R”
Return Lx
end
end
end
end
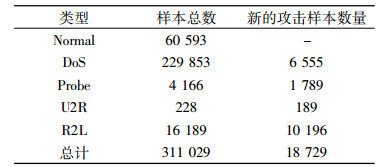
3 实验结果与分析 3.1 数据集本文采用KDD CUP 99中的“10% KDD CUP 99 training set”作为模型的训练数据, KDD CUP 99数据集[14]是网络安全研究人员公认的数据集, 测试数据和训练数据有着不同的概率分布, 测试数据集包含了一些未出现在训练数据中的攻击类型, 使入侵检测更具有现实性。该数据集有41个不同的定量和定性的特征, 分为5种不同的类, 分别是一种正常类型和4种攻击类型(DoS,Probe,U2R和R2L)。由于该训练数据集较大,随机选择了6 480条记录作为训练数据。另外,采用其中的“KDD CUP 99 corrected labeled test data set”作为测试数据集对算法进行评估, 如表 1所示, 该测试集有一些新的攻击, 但是在训练集中并未显示。
|
|
表 1 “KDD CUP 99 corrected labeled test data set”样本信息 Tab. 1 The sample distributions on the test data with the corrected labeled of KDD CUP 99 |
在入侵检测系统中, 通常用准确率、检测率、误报率、F-measure、平均建模时间和平均检测时间作为评估系统的指标。准确率、检测率、误报率定义分别如下:

|
其中, TP指实际攻击被识别为攻击行为的数量, TN指实际正常记录被识别为正常记录的数量, FP指实际正常记录被识别为攻击行为的数量, FN指实际攻击被识别为正常记录的数量。
F-measure是召回率(Recall)和查准率(Precision)之间的调和函数[15], 用来评价分类器的性能, 也是检查系统准确率的一个重要指标。本文将召回率和查准率分配相同的权重, 定义如下:
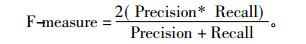
|
其中, Precision是预测为攻击且实际为攻击的比例, Precision越高, 则说明系统的误报率(FPR)越低,其定义为
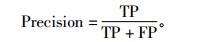
|
Recall是指攻击被正确识别的比例, 也是衡量检测系统性能另一个重要的指标, 定义为
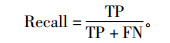
|
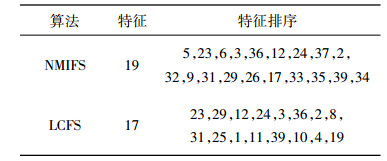
基于第2节中的理论依据, 采用KDD CUP 99数据集, NMIFS算法和LCFS算法的特征排序结果如表 2所示, 表中的数字1~41分别代表KDD CUP 99数据集中41个特征。如表 3所示, 对比NMIFS算法和LCFS算法在建模和测试时间方面, LCFS算法所需时间几乎是NMIFS算法的2倍, 说明NMIFS算法降低了特征选择进程中的计算成本, 提高了运行效率。
|
|
表 2 NMIFS算法和LCFS算法的特征选择结果对比 Tab. 2 Comparison of feature selection results of NMIFS algorithm and LCFS algorithm |
|
|
表 3 NMIFS算法和LCFS算法的建模和测试时间结果对比 Tab. 3 Comparison of modeling and test time results of NMIFS algorithm and LCFS algorithm |
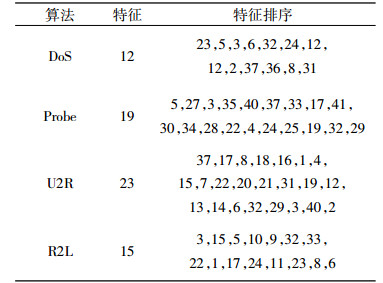
在本实验中, 文献[7]特征选择算法MMIFS的冗余参数β=0.5。在估计MI时, 文献[16]用实验证明了, 当K=6时, MI能达到最佳估计值。经实验,4种攻击类型DoS,Probe,U2R和R2L的特征排序结果如表 4所示。
|
|
表 4 KDD CUP 99中4类攻击特征排序结果 Tab. 4 Feature ranking results for the four types of attacks on the KDD CUP 99 dataset |
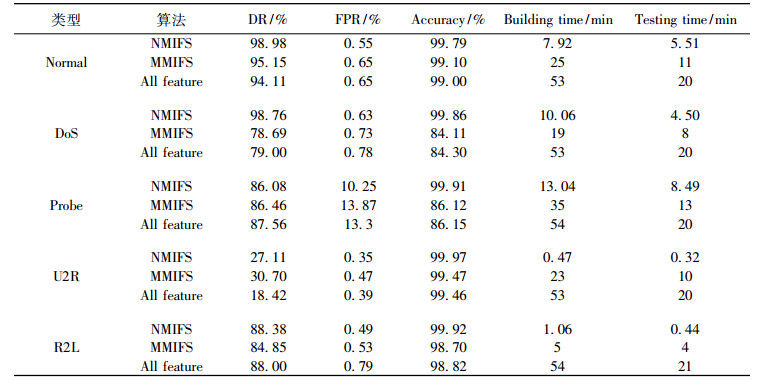
为了评估特征选择算法NMIFS的性能和有效性,将其与特征选择算法MMIFS及未使用特征选择算法进行对比, 3种情况均采用同种分类器LSSVM, 结果如表 5所示。NMIFS算法在误报率(FPR)和分类准确率(Accuracy)方面均优于这两种算法, 在检测率(DR)方面, NMIFS算法在Probe和U2R攻击中略低于MMIFS算法, 但并不影响该算法的整体水平, 且在其他攻击类型中检测率都优于对比算法。同时, 在建模时间和检测时间方面, NMIFS算法明显低于对比算法。因此, 将特征选择算法NMIFS应用于入侵检测中, 不仅能提高系统的精度, 还能降低计算复杂度。
|
|
表 5 准确率、检测率、误报率、平均建模时间和平均测试时间的结果对比 Tab. 5 Comparison of results of accuracy, detection rate, false positive rate, average modeling time and average test time |
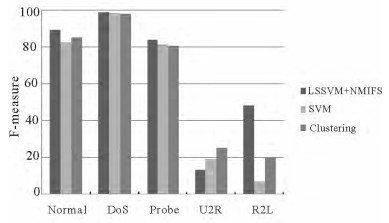
为了进一步验证NMIFS特征选择算法结合LSSVM分类算法应用于入侵检测系统的检测性能,本文分别将入侵检测系统中两种常见的挖掘算法:SVM[17]和Clustering[18]与LSSVM+NMIFS入侵检测系统对比, 对比结果如表 6所示, LSSVM+NMIFS系统在5种类型中的检测率大体优于其他系统, 特别是在U2R和R2L这两类特殊且难以检测的攻击类型中, 分别以22.1%和88.38%的检测率高于基于SVM和Clustering算法的系统, 在基于Clustering的入侵检测系统中, Normal、DoS和Probe这3类攻击的检测率相对略高。但是, 从平均水平来说, LSSVM+NMIFS系统能实现最高的检测率。另外, 针对SVM,Clustering与LSSVM+NMIFS这3种算法的F-measure也做了对比分析, 如图 1所示。由图 1可得, 在Normal,DoS,Probe和R2L这4种类型中, LSSVM+NMIFS算法分别以89.31%,99.27%,84.16%和48.13%的F-measure值明显高于对比算法。在U2R攻击类型中, Clustering算法的F-measure值相对较高,为13.26%,但是, 从整体结果看, LSSVM+NMIFS算法的性能优于SVM和Clustering算法。
|
|
表 6 各入侵检测系统的检测率对比结果 Tab. 6 Comparison results of detection rate of each intrusion detection system |
|
图 1 SVM,Clustering与LSSVM+NMIFS这3种算法的F-measure Fig. 1 Comparison of F-measure results of three algorithms of SVM, clustering and LSSVM+NMIFS |
分类方法的鲁棒性和特征选择算法的有效性是建立IDS的两个主要部分。本文提出了一种新的高效的特征选择算法NMIFS, 该算法先选出最优子集, 然后结合LSSVM分类算法以建立IDS, 且该算法能处理线性和非线性相关的数据。使用入侵检测数据集KDD CUP 99对算法进行了验证和评估。对比MMIFS特征选择算法和未经过特征选择的算法以及NMIFS算法在检测率、误报率、分类准确率、建模和检测时间方面均为最优, 这说明NMIFS算法不仅能提高分类算法的准确率, 提高检测的精度, 还能降低计算复杂度。同时, 对比常用在入侵检测系统的挖掘算法, NMIFS算法与LSSVM分类算法相结合, 明显提高了入侵检测系统的检测率。虽然本文提出了性能相对较优的特征选择算法NMIFS, 但是在搜索策略方面还需要进一步优化完善, 同时, 不平衡的样本分布对入侵检测的影响也需要纳入下一步工作中。
| [1] |
AMBUSAIDI M A, HE X, NANDA P. Unsupervised feature selection method for intrusion detection system[C]//IEEE Trustcom/BigDataSe/ISPA. IEEE Computer Society, 2015: 2497-2507.
|
| [2] |
HASANI S R, OTHMAN Z A, KAHAKI S M M. Hybrid feature selection algorithm for intrusion detection system[J]. Journal of Computer Science, 2014, 10(6): 1015-1025. DOI:10.3844/jcssp.2014.1015.1025 |
| [3] |
江颉, 王卓芳, 陈铁明, 等. 自适应AP聚类算法及其在入侵检测中的应用[J]. 通信学报, 2015, 36(11): 118-126. DOI:10.11959/j.issn.1000-436x.2015242 |
| [4] |
AHMAD I, HUSSAIN M, ALGHAMDI A, et al. Enhancing SVM performance in intrusion detection using optimal feature subset selection based on genetic principal components[J]. Neural Computing and Applications, 2014, 24(7): 1671-1682. |
| [5] |
王晨曦, 林耀进, 刘景华, 等. 基于最近邻互信息的特征选择算法[J]. 计算机工程与应用, 2016, 52(18): 74-78. DOI:10.3778/j.issn.1002-8331.1412-0214 |
| [6] |
董红斌, 滕旭阳, 杨雪. 一种基于关联信息熵度量的特征选择方法[J]. 计算机研究与发展, 2016, 53(8): 1684-1695. |
| [7] |
AMIRI F, REZAEI YOUSEFI M, LUCAS C, et al. Mutual information-based feature selection for intrusion detection systems[J]. Journal of Network & Computer Applications, 2011, 34(4): 1184-1199. |
| [8] |
AMBUSAIDI M A, HE X, TAN Z, et al. A novel feature selection approach for intrusion detection data classification[C]//2014 IEEE 13th International Conference on Trust, Security and Privacy in Computing and Communications. IEEE, 2014: 82-89.
|
| [9] |
HOQUE N, BHATTACHARYYA D K, KALITA J K. MIFS-ND: A mutual information-based feature selection method[J]. Expert Systems with Applications, 2014, 41(14): 6371-6385. DOI:10.1016/j.eswa.2014.04.019 |
| [10] |
LIN Y, HU X, WU X. Quality of information-based source assessment and selection[J]. Neurocomputing, 2014, 133: 95-102. DOI:10.1016/j.neucom.2013.11.027 |
| [11] |
ROJAS-LIMA J E, DOMÍNGUEZ-PACHECO A, HERNÁNDEZ-AGUILAR C, et al. Statistical analysis of photopyroelectric signals using histogram and kernel density estimation for differentiation of maize seeds[J]. International Journal of Thermophysics, 2016, 37(9): 1-10. |
| [12] |
ZHANG T, WANG J. Network intrusion detection based on cooperative quantum-behaved particle swarm algorithm and least square support vector machine[J]. Computer Engineering & Applications, 2015, 13(4): 350-360. |
| [13] |
EID H F, HASSANIEN A E, KIM T H, et al. Linear Correlation-Based Feature Selection for Network Intrusion Detection Model[M]//Advances in Security of Information and Communication Networks.Berlin: Springer, 2013: 240-248.
|
| [14] |
UCI machine learning repository[DB/OL][2016-03-12].http://archive.ics.uci.edu/ml/datasets/KDD+Cup+1999+Data.
|
| [15] |
LEVENE M. Search engines: Information retrieval in practice[J]. The Computer Journal, 2011, 54(5): 831-832. DOI:10.1093/comjnl/bxq039 |
| [16] |
KRASKOV A, STÖGBAUER H, GRASSBERGER P. Estimating mutual information[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2003, 69(6): 279-307. |
| [17] |
HORNG S J, SU M Y, CHEN Y H, et al. A novel intrusion detection system based on hierarchical clustering and support vector machines[J]. Expert Systems with Applications, 2011, 38(1): 306-313. DOI:10.1016/j.eswa.2010.06.066 |
| [18] |
REN W, HU L, ZHAO K, et al. A multiple-level hybrid intrusion detection system based on hierarchical clustering and decision trees[J]. Journal of Computational Information Systems, 2013, 9(13): 5421-5428. |
 2017, Vol. 47
2017, Vol. 47
 , 王海花
, 王海花