出租车是城区市民短途出行的一个重要交通工具,而在我国许多大型中心城市,普遍存在供求不匹配而引发的打车难现象。打车难最主要的原因是出租车供不应求,即出租车供应量不足且乘客打车需求量巨大, 尤其是早晚上下班高峰时段,城市大型商业中心区域的高需求与出租车资源的匹配程度严重不符。为了使出租车资源的供给与市民出行的需求能够达到基本的供求平衡,使之既能保证出租车经营企业的合理经济收益,又能满足市民方便出行的需求,这就需要对城市出租车资源进行合理规划,增强出租车资源与乘客的供求匹配程度。为此,王宇以西安市区为例,探讨了出租车资源实际供给率低的原因[1];费威等利用出租车资源供给和需求水平指标,分析了大连市出租车资源“供求匹配”程度,并对出租车资源规划提出了一些启发性的建议[2];孙辉泰等对影响城市出租车供求关系的相关因素进行了分析,提出开放竞争式管理、增加出租车资源供给、提高出租车利用率以及价格机制等增加乘客出行需求与出租车资源的规划程度[3];周小梅、邵燕斐、李艳梅等同样提出通过出租车市场的竞争博弈来实现资源优化匹配以最大化社会经济效益,并介绍了对出租车资源进行合理规划的价格机制[4-6];杜剑平等研究了“互联网+”时代深圳市出租车资源的规划问题,分析了打车公司平台提供的出租车补贴方案对资源规划的影响并设计了补贴方案设计模型[7]。这些研究为一些大型城市在出租车供应方面提供了许多有意义的参考,但较少体现对出租车资源供求匹配程度的模型化度量与评价。
本文以西安市主城区为例,将城区划分为3个区域 (1个中心区和2个郊区), 再将一天分为3个时段来研究出租车资源规划问题。根据西安各城区人口量和万人出租车拥有量近似模拟出初始的潜在乘客需求量和出租车供给量相关数据,给出了出租车空驶时间和乘客满意度函数等相关模型;接着为分析不同时空下出租车资源的供求匹配程度,建立了以总乘客满意度和出租车空驶时间加权组合为目标的非线性最优化模型,通过MATLAB软件求解计算后,对出租车资源的规划程度进行分析评价,随后分析了分时段打车费的合理性。
1 西安出租车资源规划分析 1.1 相关符号令:I表示时间段指标集, J表示城市区域划分指标集;
xij表示第i时段j区域出租公司出租车供给量 (辆/时段);
qij=qij(eij) 表示第i时段j区域乘客需求量 (人·次/时段),其中:
eij=eij(Tij, sij, Pij) 表示第i时间段j区域的单位乘客满意度 (假设以时间为单位),其中:sij表示该时段区域出租车补贴,Pij表示该时段区域内乘客的平均打车成本,Tij=Tij(xij) 表示第i时段j区域的乘客平均等待时间;并且有:
gij=gijsij, xij, qij表示第i时间段,第j区域的出租车空驶时间,其中:
β表示乘客最大等待时间阙值。
1.2 出租车资源规划指标本文以乘客满意度和出租车空驶时间为指标,分析不同时段-区域内出租车资源的“供求匹配”程度。假定乘客满意度和出租车空驶时间是影响出租车资源供给匹配程度的主要指标,忽略其他影响因素。并以一天时间为研究周期,可分为3个时段:时段1:07:30-09:00, 17:00-21:30(早晚上下班高峰时段);时段2:09:00-17:00(白天非高峰期时段);时段3:21:30-24:00, 0:00-07:30(夜间时段)。西安市城区仅考虑3个区域:区域1:新城-碑林; 区域2:莲湖-雁塔; 区域3:未央-灞桥。
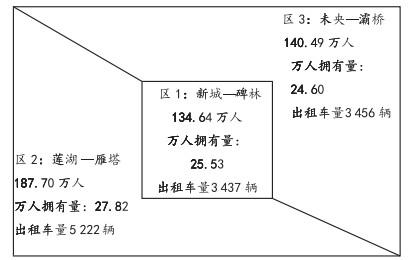
首先确定每个时段区域乘客满意度eij以及出租车的平均空驶时间gij的相关决定因素,随后以打车系统内乘客总体满意程度和出租车总空驶时间加权最大为目标函数作为我们所要建立的指标,并以该指标作为判断供求匹配程度的标准。考虑到现实情形下每个时段区域乘客的等待时间不会太久,因此,本文建立的优化模型的约束条件为每个时段区域乘客等待时间不超过一个预先给定的阙值β(小时),并添加出租车供给量xij非负限制,以保证模型的合理性;最后我们根据图 1给定的西安主城区域网络来分析模型所获得的出租车资源供求匹配的合理程度。
|
图 1 西安主城各区信息图 |
为了评价不同时段区域出租车资源的供求匹配程度,我们以所有时段区域的总需求匹配程度为目标建立如下的非线性最优化模型:
| $ \text{max}z\left( x \right)={{\alpha }_{1}}\sum\limits_{i\in I}{\sum\limits_{j\in J}{{{e}_{ij}}\cdot {{q}_{ij}}({{e}_{ij}})}}-{{\alpha }_{2}}\sum\limits_{i\in I}{\sum\limits_{j\in J}{{{x}_{ij}}\cdot {{g}_{ij}}({{s}_{ij}}, {{x}_{ij}}, {{q}_{ij}})}} $ | (1) |
| $ s.t.\text{ }{{T}_{ij}}({{x}_{ij}}, {{q}_{ij}})\le \beta, \forall i\in I, j\in J, $ | (2) |
| $ {{x}_{ij}}\ge 0, \forall i\in I, j\in J。 $ | (3) |
其中:(1) 式为打车系统内所有乘客的满意度与出租车总空驶时间加权和,用来表示出租车资源供求匹配程度的合理性指标,z越大表明出租车与乘客的供求匹配程度越合理,即乘客满意度较高且出租车的空驶时间较低;(2) 式表示每个时段区域的乘客平均等待时间不超过给定时间阙值β;(3) 式表示各时段区域出租车供给量非负。
2 西安市区出租车资源供求匹配程度评价图 1给定西安主城各区的出租车万人拥有量、人口总量 (万人)、出租车数以及各区域分布图。为了便于数值模拟分析,对每个时间段i∈I和每个区域j∈J,取
需求-满意度函数:
| $ {{q}_{ij}}({{e}_{ij}})=q_{ij}^{\text{max}}\left( 1-\frac{{{a}_{2}}}{{{e}_{ij}}} \right)。 $ | (4) |
其中:qijmax表示第i时段j区域可出行的潜在乘客需求量。
乘客平均等待时间函数:
| $ {{T}_{ij}}({{x}_{ij}})={{a}_{1}}+{{b}_{1}}\sqrt{{{q}_{ij}}}-{{c}_{1}}\sqrt{{{x}_{ij}}}。 $ | (5) |
出租车空驶时间函数:
| $ {{g}_{ij}}({{s}_{ij}}, {{x}_{ij}}, {{q}_{ij}})=24(1-\text{exp}(-{{b}_{2}}{{x}_{ij}}))\cdot \frac{{{c}_{2}}}{(1+{{s}_{ij}}){{q}_{ij}}}。 $ | (6) |
乘客满意度函数:
| $ {{e}_{ij}}({{T}_{ij}}, {{s}_{ij}}, {{P}_{ij}})={{a}_{3}}{{s}_{ij}}-{{b}_{3}}{{T}_{ij}}-{{c}_{3}}{{P}_{ij}} $ | (7) |
取函数
| $ {{\bar{z}}_{ij}}\left( x \right)={{\alpha }_{1}}{{e}_{ij}}\cdot {{q}_{ij}}({{e}_{ij}})-{{\alpha }_{2}}{{x}_{ij}}\cdot {{g}_{ij}}({{s}_{ij}}, {{x}_{ij}}, {{q}_{ij}}) $ | (8) |
为指标来评价不同时段-区域出租车资源与乘客需求的匹配程度。
为了便于数值实验和分析,本文取:
a1=0.06, a2=1, a3=10; b1=0.022, b2=0.01, b3=0.4;c1=0.02, c2=0.01, c3=0.5;α1=1, α2=0.6;β=1;sij=2(这里2为出租车固定基础补贴)。
设各区域乘客潜在需求量为出租车供给量的1.5倍,实际需求为潜在需求量的0.8倍,设各区域时段1、时段2、时段3的乘客需求比6:3:1。不同时段区域的出行成本矩阵为
| 表 1 西安市城区各时段的评价等级表 |
通过LINGO软件进行编程运算,以模型 (6) 获得最优解所对应的不同时段区域的供求匹配指标值zij*为最优评价标准,将评价等级分为四个级别:优为[0.9zij*, zij*]、良为[0.75zij*, 0.9zij*]、合格为[0.6zij*, 0.75zij*]、不合格为[0.6zij*]以下。其评价等级如表 1所示。
从表 1中我们可以发现,合理的出租车资源规划可以有效增加供求匹配程度,由此可知我们所建立的模型是合理的。在表 1中,有部分时段区域 (例如时段2区域1、时段3区域1、时段3区域2) 的供求匹配程度指标值大于最优指标值,这是因为我们的优化目标是整个打车系统中供求匹配程度指标而不是以每个时段区域为优化目标,因此出现这种情形并不奇怪。但由于我们模型需要的参数比较多,因此实际应用时需要严格矫正这些参数,以达到出租车资源的最优供求匹配程度。通过模拟仿真数据显示,时段1区域3出租车与乘客的供求匹配程度比较差,说明该时段区域乘客打车满意度较低或者出租车空驶时间较长。由于文中是根据西安各城区人口量和万人出租车拥有量近似模拟出初始的潜在乘客需求量和出租车供给量相关数据,仿真结果存在一定的误差,在后续研究中,可采用文献[7]中GPS全球定位方式记录出租车的载客状态和行驶区域相关数据,即第i时段j区域出租车实时数据向量Dij为:
| $ ~{{D}_{ij}}=\left( C, L, B, S, V, \theta \right)。 $ | (9) |
其中:C表示出租车牌号; (L, B) 表示出租车所在区域的经度和纬度;(S, V) 表示出租车满载和空载的状态,如果出租车满载,则有 (S, V)=(1, 0),如果空载,则有 (S, V)=(0, 1);θ表示出租车所在区域的方向角。
为有效改善出租车资源与乘客的供求匹配程度,在出租车司机与乘客两方面根据不同时段与不同区域来制定不同的打车费用。例如,在时段1与区域1应收取更高的打车费用,以缓解在中心区域和高峰期时段的交通拥堵和打车供不应求问题,促使部分乘客延缓出行或选择其他公共交通工具,倡导绿色交通出行模式[8];在时段2与区域2则可以按平时计价收费,以分流高峰期与中心区域的打车需求,而在时段3与区域3,对出租车司机提供一定的补贴以鼓励出租车向远离中心区域的城郊流动,进而满足该时段区域的乘客打车难问题。
分时段区域收费的合理性表现在:
(1) 有利于缓解高峰期与中心区域交通拥堵和打车供不应求问题。由于上下班高峰期时段和城市中心区域车流密度非常大,交通异常拥堵,同时噪音尾气等污染严重影响该时段区域的空气质量,为此,设计这种补贴方案可适当减少乘客打车率,从而降低出租车在该时段区域的进出流量。
(2) 在非高峰时段或非中心区域的收费方式可分流高峰期与中心区域的打车需求,使部分乘客和出租车司机乐于在非中心区域与非高峰时段打车和工作,从而在一定程度上缓解打车难。
(3) 在夜间时段与郊区应适当给出租车司机一定的载客补贴,从而促使出租车向远离中心区域的城郊流动以缓解该时段区域的乘客打车难问题。
3 结语本文建立的是非线性最优化模型,运用了线性加权,使用MATLAB软件、LINGO软件编写相关程序,用模拟数据的方法解决数据不充分的问题,简单易懂。本模型主要建立了出租车和乘客供求匹配程度的合理性指标,对出租车资源的供求匹配程度进行了量化与模型化评价,并对不同时间-区域出租车资源的供求匹配程度进行了等级化处理。该模型基于严密的数学建模,求解过程严谨,可信度较高,说服力较强。但由于本文数据信息量不足,致使我们所建数学模型的数据是模拟数据,因此即使经过严密的数学建模和严谨的编程计算,模型在代入模拟数据后还会有一定的误差,因此在实际分析中应当做大量的实况调查,以提高数据的精确度,从而得到更加切合实际情况的建模成果,提出更合理的解决措施。本文模型只考虑了影响打车难的两个重要指标,没有考察出租车行驶效率和有效行驶里程等因素,为此在以后的研究中,考虑应该更加全面,使模型中含有更多指标并分析出租车流和乘客流的转移模式。[9]
| [1] | 王宇. 对城市打的难现象的剖析——基于西安市出租车市场供求失衡问题的分析[J]. 价格理论与实践, 2011(11): 15–16. |
| [2] | 费威, 马跃, 李泊宁, 等. 我国城市出租车资源供求匹配程度研究[J]. 河北科技大学学报 (社会科学版), 2016(1): 1–7. |
| [3] | 孙辉泰, 贺亦军, 邹普尚, 等. 基于供求关系的缓解"打车难"策略研究[J]. 交通企业管理, 2014(10): 1–3. DOI:10.3963/j.issn.1006-8864.2014.10.001 |
| [4] | 周小梅, 田定远. 对我国城市出租车行业管制问题的思考——从出租车司机和乘客利益变化角度的分析[J]. 价格理论与实践, 2011(8): 29–30. |
| [5] | 邵燕斐, 王小斌. 基于博弈论视角的出租车价格管制困境破解[J]. 开发研究, 2014(2): 139–143. |
| [6] | 李艳梅, 杨涛. 北京市出租车市场管制模式的福利分析[J]. 北京交通大学学报 (社会科学版), 2008(3): 36–42. |
| [7] | 杜剑平, 韩中庚. "互联网+"时代的出租车资源配置模型[J]. 数学建模及其应用, 2015(4): 40–49. |
| [8] | 魏媛星. 均等化视角下地方政府间交通公共服务合作供给策略研究[J]. 渭南师范学院学报, 2016, 31(6): 80–85. |
| [9] | 刘炳全. 基于诱导信息的交通堵塞路径流量转移模型[J]. 渭南师范学院学报, 2012, 27(2): 41–43. |