利用有理样条进行保形插值是几何造型领域中的研究热点之一[1-8]。文献[4-6]介绍的保形有理四次样条插值函数节点处导数的算法为构造光顺的保形有理四次样条插值曲线,以形状控制参数和节点处的导数为决策变量,以插值曲线应变能最小为目标函数,以插值函数保形以及形状控制参数和节点处的导数大于0作为约束条件,建立优化模型,给出插值算法是求解获得应变能最小的保形有理四次样条插值曲线。
1 插值函数[4]给定数据{(xi, fi), i=1, 2, …, n},其中:fi为被插值函数在节点xi处的函数值,此处令x1<x2 < … < xn。记hi=xi+1-xi,Δi=(fi+1-fi)/hi;令t=(x-xi)/hi,当x∈[xi, xi+1]时,t∈[0,1],i=1, 2, …, n-1,构造分子是四次多项式、分母是一次多项式的有理样条插值曲线s(x),s(x) 定义如下:
| $ s\left( x \right) = s\left( {{x_i} + {h_i}t} \right) \equiv S\left( t \right)\left| {_{[{t_i}, {t_{i + 1}}]}} \right. = \frac{{{P_i}\left( t \right)}}{{{Q_i}\left( t \right)}}, i = 0, 1, 2, \ldots, n -1。 $ | (1) |
其中:
| $ {P_i}\left( t \right) = {\alpha _i}{f_i}{\left( {1-t} \right)^4} + {U_i}{\left( {1-t} \right)^3}t + {V_i}{\left( {1-t} \right)^2}{t^2} + {W_i}\left( {1 - t} \right){t^3} + {\beta _i}{f_{i + 1}}{t^4}, $ | (2) |
| $ \begin{array}{l} {Q_i}\left( t \right) = {\alpha _i}\left( {1-t} \right) + {\beta _i}t, {\rm{ }}\\ {U_i} = \left( {3{\alpha _i} + {\beta _i}} \right){f_i} + {\alpha _i}{d_i}{h_i}, {\rm{ }}\\ {V_i} = 3{\beta _i}{f_{i + 1}} + 3{\beta _i}{f_i}。 \end{array} $ | (3) |
插值函数s(x) 在节点xi处的一阶导数值为di,αi, βi被称为形状控制参数且αi>0, βi>0。
由 (2)(3) 式易知,有理样条插值s(x) 满足下列插值性质:
| $ s\left( {{x_i}} \right) = {f_i}, i = 0, 1, \cdots, n。 $ | (4) |
如果f(x) 在区间[a, b]上有x1 < x2 < … < xn, f1≤f2≤...≤fn或Δi≥0,那么函数f(x) 在区间[a, b]上单调递增。选取导数值di时必须满足:
| $ {d_i} \ge 0, i = 1, 2, \cdots, n。 $ | (5) |
在区间[xi, xi+1]上,s(x) 单调递增的充要条件为:
| $ s\prime \left( x \right) \ge 0, i = 0, 1, \cdots, n-1。 $ | (6) |
对 (1) 式中定义的插值函数s(x) 求导:
| $ s\prime \left( x \right) = S\prime \left( t \right){h_i}^{- 1} = \frac{{\sum\limits_{j = 0}^4 {{Q_{ij}}{{\left( {1- t} \right)}^{4- j}}{t^j}} }}{{{{\left[{{\alpha _i}\left( {1-t} \right) + \beta t} \right]}^2}}}。 $ | (7) |
其中:
因为 (7) 式给出的插值函数s(x) 的导数s′(x) 的分母恒为正,所以只需s′(x) 的分子大于0即可。当di≥0时,有Qi1≥0, Qi4≥0,因此插值函数s(x) 单调的充要条件为:Qij≥0, j=1, 2, 3。即
| $ \begin{array}{l} {Q_{i1}} = 2{\alpha _i}^2\left( {3{\Delta _i}-{d_i}} \right) \ge 0, {\rm{ }}\\ {Q_{i2}} = 3{\alpha _i}{\beta _i}\left( {4{\Delta _i}-{d_i}-{d_{i + 1}}} \right) \ge 0, {\rm{ }}\\ {\rm{ }}{Q_{i3}} = 2{\beta _i}^2\left( {3{\Delta _i} - {d_{i + 1}}} \right) > 0. \end{array} $ | (8) |
由 (8) 式得到函数s(x) 单调的充要条件为:
| $ {d_i} \le 3{\Delta _i}, {d_{i + 1}} \le 3{\Delta _i}, {d_i} + {d_{i + 1}} \le 4{\Delta _i}。 $ | (9) |
由文献[8]得出下列结论:
已知单调递增数据f1≤f2≤…≤fn, 导数值di≥0, 只要di满足 (9) 式时,就存在含有正参数αi,βi的有理四次样条插值函数s(x)∈C1[a, b],并且是单调递增的。
3 有理四次样条插值函数二阶连续对 (1) 式求二阶导数并化简可得:
| $ s''\left( x \right) = S''\left( t \right){h_i}^{- 2} = \frac{{\sum\limits_{j = 0}^4 {{B_{ij}}{{\left( {1- t} \right)}^{4- j}}{t^j}} }}{{{h_i}{{\left[{{\alpha _i}\left( {1-t} \right) + {\beta _i}t} \right]}^3}}}。 $ | (10) |
其中:
| $ \begin{array}{l} {B_{i0}} = 2{\alpha _i}^3\left( {3{\Delta _i}-2{d_i}} \right)-2{\alpha _i}^2{\beta _i}{d_i}, {\rm{ }}\\ {B_{i1}} = 6{\alpha _i}^2{\beta _i}\left( {3{\Delta _i}-{d_{i + 1}}} \right) + 2{\alpha _i}^3\left( {{d_i} - 3{\Delta _i}} \right) - 8{\alpha _i}^2{\beta _i}{d_i}, {\rm{ }}\\ {B_{i2}} = 6{\alpha _i}^2{\beta _i}\left( {{d_i} - 3{\Delta _i}} \right) + 6{\alpha _i}{\beta _i}^2\left( {3{\Delta _i} - {d_{i + 1}}} \right), \\ {B_{i3}} = 6{\alpha _i}{\beta _i}^2\left( {{d_i} - 3{\Delta _i}} \right) + 2{\beta _i}^3\left( {3{\Delta _i} - {d_{i + 1}}} \right) + 8{\alpha _i}{\beta _i}^2{d_{i + 1}}, {\rm{ }}\\ {B_{i4}} = 2{\beta _i}^3\left( {2{d_{i + 1}} - 3{\Delta _i}} \right) + 2{\alpha _i}{\beta _i}^2{d_{i + 1}}。 \end{array} $ | (11) |
因此有
| $ s''\left( {{x_{i-}}} \right) = \frac{{4\beta _{i-1}^3{d_i} + 2{\alpha _{i-1}}\beta _{i - 1}^2{d_i} - 6\beta _{i - 1}^3{\Delta _{i - 1}}}}{{{h_{i - 1}}\beta _{i - 1}^3}} = \frac{{4{\beta _{i - 1}}{d_i} + 2{\alpha _{i - 1}}{d_i} - 6{\beta _{i - 1}}{\Delta _{i - 1}}}}{{{h_{i - 1}}{\beta _{i - 1}}}}。 $ | (12) |
| $ s''\left( {{x_{i + }}} \right) = \frac{{6\alpha _i^3{\Delta _i}-4\alpha _i^3{d_i}-2\alpha _i^2{\beta _i}{d_i}}}{{{h_i}\alpha _i^3}} = \frac{{6{\alpha _i}{\Delta _i}-4{\alpha _i}{d_i} - 2{\beta _i}{d_i}}}{{{h_i}{\alpha _i}}}。 $ | (13) |
由函数s(x) 在xi处二阶连续,可得
| $ {d_i} = \frac{{{h_i}{\Delta _{i - 1}} + {h_{i - 1}}{\Delta _i}}}{{\frac{2}{3}\left( {{h_{i - 1}} + {h_i}} \right) + \frac{1}{3}\left( {\frac{{{\beta _i}}}{{{\alpha _i}}}{h_{i - 1}} + \frac{{{\alpha _{i - 1}}}}{{{\beta _{i - 1}}}}{h_i}} \right)}}。 $ | (14) |
由此得出如下结论:
当插值导数di满足 (14) 式时,含有形状控制参数αi, βi的有理四次样条插值函数s(x) 在区间[a, b]上二阶连续。[9]
4 插值曲线的应变能插值曲线的研究主要应用在物体外形设计上,因此插值曲线不仅要求过插值节点,还要求曲线能够保光顺性、保凹凸性等。研究曲线光顺性会发现光顺准则是最基本的问题,人们在不同的实际问题中,对曲线光顺的要求不同,使得对曲线光顺的认识也不同。一般认为应变能最小的曲线是光顺的,在曲线光顺的研究中常常以曲线能量较小作为约束条件。[10-12]
插值函数s(x) 在[x0, xn]区间上C2-连续曲线的应变能定义如下:
| $ \smallint _{{x_0}}^{{x_n}}{\left[{s''\left( x \right)} \right]^2}dx = \sum\limits_{i = 0}^{n - 1} {\smallint _{{x_i}}^{{x_{i + 1}}}{{\left[{s''\left( x \right)} \right]}^2}dx}, $ | (15) |
积分化简得
| $ \sum\limits_{i = 0}^{n- 1} {\smallint _{{x_i}}^{{x_{i + 1}}}{{\left[{s''\left( x \right)} \right]}^2}} dx = \sum\limits_{i = 0}^{n -1} {\frac{{4\left( {{A_i}\alpha _i^2 + {B_i}\beta _i^2 + {C_i}{\alpha _i}{\beta _i}} \right)}}{{5h_i^3{\alpha _i}{\beta _i}}}}, $ | (16) |
其中:
| $ \begin{array}{*{20}{l}} {{A_i} = h_i^2d_{i + 1}^2,}\\ {{B_i} = h_i^2d_i^2,}\\ \begin{array}{l} {C_i} = 15{h_i}{f_i}{d_i} + 15{h_i}{f_i}{d_{i + 1}} + 5h_i^2d_i^2 + 5h_i^2d_{i + 1}^2 - 15{h_i}{f_{i + 1}}{d_i} - \\ 15{h_i}{f_{i + 1}}{d_{i + 1}} + 3h_i^2{d_i}{d_{i + 1}} + 15f_i^2 + 15f_{i + 1}^2 - 30{f_i}{f_{i + 1}}. \end{array} \end{array} $ |
为构造光顺的保形有理四次样条插值曲线,以形状控制参数αi,βi和节点处的导数di为决策变量,以插值曲线应变能最小为目标函数,以插值函数保形以及形状控制参数αi,βi和节点处的导数di大于0作为约束条件,建立优化模型
| $ \smallint _{{x_0}}^{{x_n}}{\left[{s''\left( x \right)} \right]^2}dx = {\rm{min}} $ | (17) |
| $ {\rm{ }}s.t.\;\;\;{\alpha _i}, {\beta _i} > 0, i = 0, 1, \cdots, n-1, $ | (18) |
| $ {\rm{ }}{d_i} > 0i = 0, 1, \cdots, n, $ | (19) |
| $ {d_i} \le 3{\Delta _i}, {d_{i + 1}} \le 3{\Delta _i}, {d_i} + {d_{i + 1}} < 4{\Delta _i}, i = 0, 1, \cdots, n-1. $ | (20) |
求解此优化模型得最优参数αi, βi和di,进一步得到光顺的保形有理四次样条插值曲线。
由文献[13-14]知,保形有理四次样条插值函数的误差有以下结论:
定理1 设f(x)∈C2[a, b],s(x) 是f(x) 如 (1) 式所定义的有理样条插值函数,对给定的αi, βi,则x∈[xi, xi+1], i=0, 1, …, n-1,有
| $ \left| {R[f]} \right| = \left\| {f''(x) -s(x)} \right\| \le \frac{{10}}{9}\left\| {f''(x)} \right\|h_i^2. $ |
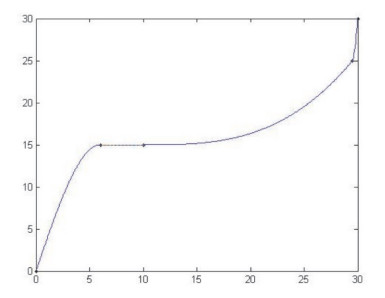
给出一组单调递增的数据x1=0, x2=6, x3=10, x4=29.5, x5=30, f(x1)=0.01, f(x2)=15, f(x3)=15, f(x4)=25, f(x5)=30。
由本文方法建立模型求解最优形状参数αi,βi和插值节点处导数di的值如表 1所示。
| 表 1 形状参数αi, βi和导数di的值 |
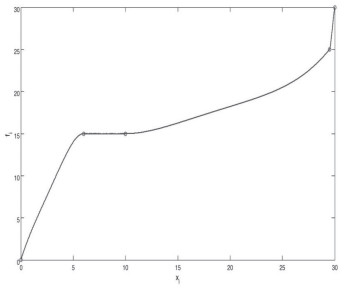
依表 1数据绘制出应变能最小且保形的有理四次样条插值曲线 (如图 1),并与文献[6]中插值法所绘制的插值曲线 (如图 2) 作对比,验证了新方法的有效性。
|
图 1 由新方法得到的有理样条插值曲线 |
|
图 2 由文献[6]得到的有理样条插值曲线 |
| [1] | Delbourgo R, Gregory J A. Shape preserving piecewise rational interpolation[J]. Siam Journal on Scientific & Statistical Computing, 1984, 6(4): 967–976. |
| [2] | Min J, Chen B K. A kind of rational quartic interpolation spline and its approximation properties[J]. Numerical Mathematics A Journal of Chinese Universities, 2007, 29(1): 57–62. |
| [3] | Han X. Convexity-Preserving Piecewise Rational Quartic Interpolation[J]. Siam Journal on Numerical Analysis, 2008, 46(2): 920–929. DOI:10.1137/060671577 |
| [4] | 王强. 有理插值样条方法及其在数字图像处理中的应用研究[D]. 合肥: 合肥工业大学博士学位论文, 2007: 41-44. |
| [5] | 邓四清, 蔡时荣, 孙宇峰. 一种带导数的有理四次插值样条曲线的区域控制[J]. 韶关学院学报, 2012, 33(12): 5–9. DOI:10.3969/j.issn.1007-5348.2012.12.001 |
| [6] | Cukup S, Baik L, Kuartik I, et al. Improved Sufficient Conditions for Monotonic Piecewise Rational Quartic Interpolation[J]. Sains Malaysiana, 2011, 40(10): 1173–1178. |
| [7] | 邓四清. 一类加权有理四次插值样条曲线的形状控制[J]. 计算机工程与应用, 2014, 50(2): 137–141. |
| [8] | 刘琳, 唐月红. 一类四次有理样条的形状控制及其逼近性质[J]. 数值计算与计算机应用, 2010, 31(4): 241–252. |
| [9] | Wang Q, Tan J Q. Rational quartie spline involving shape parameters[J]. Journal of Infmation & Computational Science, 2004(1): 127–130. |
| [10] | Duan Q, Bao F, Du S, et al. Local control of interpolating rational cubic spline curves[J]. Computer-Aided Design, 2009, 41(11): 825–829. DOI:10.1016/j.cad.2009.05.002 |
| [11] | Bao F, Sun Q, Pan J, et al. A blending interpolator with value control and minimal strain energy[J]. Computers & Graphics, 2010, 34(2): 119–124. |
| [12] | Zhang C, Zhang P, Cheng F. Fairing spline curves and surfaces by minimizing energy[J]. Computer-Aided Design, 2001, 33(13): 913–923. DOI:10.1016/S0010-4485(00)00114-7 |
| [13] | 闵杰, 陈邦考. 一种四次有理插值样条及其逼近性质[J]. 高等学校计算数学学报, 2007, 29(1): 57–62. |
| [14] | 段奇, 刘爱奎, 张玲, 等. 几种有理插值函数的逼近性质[J]. 高等学校计算数学学报, 2000, 22(1): 55–62. |