Talbot效应是一种自成像现象，通常把具有横向周期性结构物体的衍射场在纵向具有周期性的现象称为Talbot效应^[1-2]。随着现代光学的发展，近年来人们对于Talbot效应进行了很多研究，Cowley和Moodie描述了在点光源照明下光栅后形成光栅像的特点^[3]; Winthrop和Worthington基于菲涅耳-基尔霍夫积分分析了在球面波入射时平面周期性结构物体的自成像效应^[4]，认识到了Talbot效应的关键特征并给出了全面完整的解释。通过金属与光波的相互作用产生表面等离子波，可在亚波长尺度上控制光的传播，从而获得微型化的波长量级光回路，亦可制作表面等离子体光子芯片、耦合器、调制器和开关^[5-8]。除此之外，由于表面等离子体波对金属表面结构高度敏感的特性，它还被广泛应用于传感领域^[9-10]，其中包括生物传感、物理量探测、化学量探测。具体说来，可将表面等离子体波的Talbot效应应用在光互联中, 即可以把一个信号的光束照射在金属小孔阵列上，这束光的一部分耦合到表面等离子体波中，而表面等离子体波会在金属膜上形成菲涅尔衍射(Fresnel diffraction)，从而在距离一维小孔阵列的特定长度上形成Talbot像，对这些Talbot像进行不同的处理，可以得到多路信号，最后用某一元件把表面等离子体波转换成光出射，其结果就是把一路信号的光波在亚波长光学元件上转为多路信号的光波，可以广泛应用于光通信、光传感等领域^[11-12]。此理论与传统的用普通光栅对光波的分束相比较，大大减小了光学元件的尺度，为集成光学的微型化发展作出重要贡献。本文采用在金属薄膜上打出一列周期排布的小孔，并在薄膜背面用波长为632.8 nm的He-Ne激光平行照射来实现这一效应。根据偶极子模型理论推导出一维周期小孔光栅的金属膜附近的电磁场变化规律，数值模拟出一维小孔光栅后的衍射图样并进一步分析其性能特点。

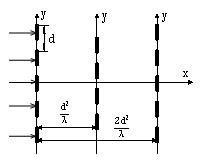
1. Talbot效应的结构 1.1. 一维周期光栅的Talbot效应

让一束单色平行光(波长为λ)垂直入射到一维周期光栅(周期为d)上，可观察到光栅后面空间中的光场强度分布，在$x = 2n\frac{{{d^2}}}{\lambda }$处(n为正整数)形成Talbot像，如图 1所示，与原光栅图样近似相同；在$x = \left( {2n - 1} \right)\frac{{{d^2}}}{\lambda }$处形成12分数Talbot像，与原光栅图样相比，在横向上平移了半个周期。

1.2. 小孔阵列的Talbot效应

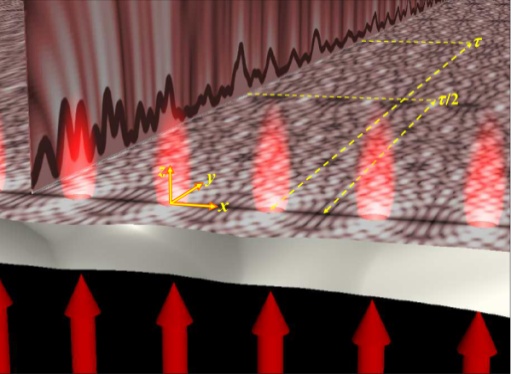
采用金属打孔方式实现一维周期小孔光栅的金属表面等离子体波的Talbot效应，如图 2所示。在平坦的金属薄膜上打出一排一维周期小孔，然后在薄膜背面用垂直入射的单色平行光照明，金属薄膜上每个小孔相当于一个次波源，能产生并向外发射表面等离子体波。因此，入射光在穿过这些周期小孔结构时，有一部分转化表面等离子体波，这些表面等离子体波沿金属表面传播，在金属薄膜上表面发生相干叠加，在小孔结构后方的周期性距离处会形成与原物(小孔结构)相似的像，产生Talbot效应。

2. 理论分析 2.1. 偶极子模型

在图 2中，金属膜上每个小孔中出射的电磁场都可以被近似成一个偶极子辐射出的电磁场，偶极子的振荡频率与入射光的频率相同，$\omega = \frac{{2\pi c}}{\lambda }$。其中：λ是入射光的波长，c为真空中光速。这种偶极子振荡可激发出表面等离子体波，表面等离子体波沿金属表面传播，其波长为${\lambda _{sp}} = \frac{\lambda }{{{\mathop{\rm Re}\nolimits} \left\{ {\sqrt {\frac{\varepsilon }{{1 + \varepsilon }}} } \right\}}}$，ε为金属介电常数。

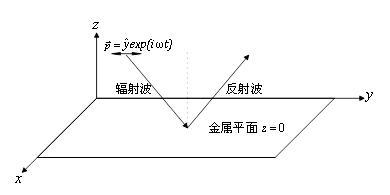
假设振荡偶极子的偶极矩模为1个单位，它处在金属平面上方且无限接近金属平面(z=0) 的位置${\vec R_0}$，如图 3所示。

偶极矩沿y轴方向$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over p} = \hat y{\rm{exp}}\left( {i\omega t} \right)$，偶极子振荡相当于一个电流源，即：

$\vec j\left( {\vec r, t} \right) = - i\omega \vec \mu {\rm{exp}}\left( { - i\omega t} \right)\delta \left( {\vec r - {{\vec R}_0}} \right)。$

(1)

根据麦克斯韦方程及自由空间中的物质方程，可得到：

$ \left\{ \begin{array}{l} \vec \nabla \times \vec E\left( {\vec r} \right)-\frac{{i\omega }}{c}\vec B\left( {\vec r} \right) = 0, \\ \vec \nabla \times \vec B\left( {\vec r} \right) + \frac{{i\omega }}{c}\vec E\left( {\vec r} \right) =-i\omega \frac{{4\pi }}{c}\vec \mu \delta \left( {\vec r-{{\vec R}_0}} \right)。 \end{array} \right. $

(2)

将电磁场$ \vec E\left( {\vec r} \right)$、$\vec B\left( {\vec r} \right)$在频域中作傅里叶展开：

$ \left\{ \begin{array}{l} \vec E\left( {\vec r} \right) = \int {d\vec k\exp \left( {i\vec k \cdot \vec r} \right)} {{\vec E}_k}, \\ \vec B\left( {\vec r} \right) = \int {d\vec k\exp \left( {i\vec k \cdot \vec r} \right)} {{\vec B}_k}。 \end{array} \right. $

(3)

由振荡偶极子向金属层辐射的电场：

$ {\vec E_{dipole}}\left( {z < {R_{0z}}} \right) =- \frac{i}{{2\pi }}\int {{d^2}\vec Q\exp \left[{i\vec Q \cdot \left( {\vec \rho-{{\vec R}_{0\rho }}} \right)} \right]} \\ \left\{ {\frac{1}{{{q_1}}}{{\vec k}_1} \times \left( {{{\vec k}_1} \times \vec \mu } \right)\exp \left[{-i{q_1}\left( {z-{R_{0z}}} \right)} \right]} \right\}, $

(4)

将电场分解成TM波和TE波，即：

$ -{\vec k_1} \times \left( {{{\vec k}_1} \times \vec \mu } \right) =-{\vec k_1} \times \left( {{{\vec k}_1} \times \hat y} \right) =-\frac{{{k_1}{q_1}{Q_y}}}{Q}{\hat e_p} + \frac{{k_1^2{Q_x}}}{Q}{\hat e_s}。 $

(5)

其中：$\left\{ {{{\hat k}_1}, {{\hat e}_p}, {{\hat e}_s}} \right\}$是空间中的一组标准正交基${\hat e_s} = \hat z \times {\hat k_1}/\left| {\hat z \times {{\hat k}_1}} \right|, {\hat e_p} = {\hat e_s} \times {\hat k_1}$。令$k'_z = \sqrt {k_1^2\varepsilon-{Q^2}} $，则p波与s波的菲涅尔反射系数分别为${r_p} = \frac{{\varepsilon {q_1}-k'_z}}{{\varepsilon {q_1} + k'_z}}$和${r_s} = \frac{{{q_1}-k'_z}}{{{q_1} + k'_z}}$。在0 < z < R_0z区域内，总场应为偶极子向金属层辐射的波${\vec E_{dipole}}\left( {z < {R_{0z}}} \right)$与金属层对${\vec E_{dipole}}\left( {z < {R_{0z}}} \right)$的反射波叠加而成。

因此，由位于${\vec r_0}$位置的单个偶极子辐射所致的金属平面附近电场强度为：

$ \left\{ \begin{array}{l} {{\vec E}_{single}}\left( {\vec r} \right) = \int {{d^2}} \vec Q\exp \left[{i\vec k \cdot \left( {\vec r-{{\vec R}_0}} \right)} \right]\vec F\left( {\vec Q} \right), \\ \vec F\left( {\vec Q} \right) = \frac{{i\lambda _0^2}}{{Q{k_z}}}\left[{-{k_z}{k_y}\left( {{{\hat e}_p} + {r_p}\hat e_p^ + } \right) + k{k_x}\left( {1 + {r_s}} \right){{\hat e}_s}} \right]。 \end{array} \right. $

(6)

其中：${\hat e_p}$是辐射波中p方向的单位矢量，$ \hat e_p^ + $是反射波中p方向的单位矢量，${\hat e_s}$是辐射波和反射波中s方向的单位矢量，$\vec k = {\vec k_1} = \frac{{2\pi }}{{{\lambda _0}}}{\hat k_1}$为自由空间中的波矢，$\vec Q = \left( {{k_x}, {k_y}} \right)$为$\vec k$在金属表面的投影，$ {k_z} = {q_1} = \sqrt {{k^2}-{Q^2}} $是$\vec k$在垂直于金属表面分量的绝对值，r_p和r_s分别为TM波和TE波的菲涅尔反射系数, $\left\{ {\hat k, {{\hat e}_p}, {{\hat e}_s}} \right\}$是空间中的一组标准正交基，${\hat e_s} = \hat z \times \hat k/\left| {\hat z \times \hat k} \right|, {\hat e_p} = {\hat e_s} \times \hat k$。

2.2. 电场的性质

根据上述计算结果(6) 式可知，关于p波的项${\hat e_p} + {r_p}\hat e_p^ + $有奇点，奇点上$\varepsilon {k_z} + k'_z = 0$，因此，可以得出表面等离子体波的色散关系：${Q_{SP}} = k\sqrt {\varepsilon /(\varepsilon + 1)} $。而表面等离子体波即是TM波(p波)，因此奇点就对应着表面等离子体波。由于${E_z}\left( {\vec r} \right)$全是由p波贡献的，并且对k_y的积分主要是对奇点进行积分，奇点又代表着表面等离子体波。可见，${\vec E_{single}}\left( {\vec r} \right)$几乎全部由表面等离子体波构成。

综上所述，偶极子无限接近金属平面，R_0z→0，当$\vec r-{\vec R_0}$取在偶极子方向(y方向)时，金属平面上的E_z值最大。为了最大化可视化效应，本实验选择在x轴方向安排一列周期性排布的偶极子阵列，它们的偶极矩都在y方向，激发的表面等离子体波主要沿y方向传播。

2.3. 小孔阵列产生的电场

理想的表面等离子体波的Talbot效应是由一列无限长的等间距排列的偶极子场叠加产生的，若第n个偶极子位置为${\vec R_n} = \left( {na, 0, 0} \right)$，则在金属平面附近产生的场：

$ {\vec E_{total}}\left( {\vec r} \right) = {\sum\limits_m {\left[{{{\vec E}_{single}}\left( {\vec r} \right)} \right]} _m}。 $

(7)

由于${\vec E_{single}}\left( {\vec r} \right)$的主要部分是它的z分量${E_z}\left( {\vec r} \right)$，故${\vec E_{total}}\left( {\vec r} \right)$的主要部分也是其z分量${\left[{{{\vec E}_{total}}\left( {\vec r} \right)} \right]_z}$。根据泊松公式得到：

$ {\left[{{{\vec E}_{total}}\left( {\vec r} \right)} \right]_z} = \sum\limits_m {A\exp \left( {i2\pi mx/a} \right)\exp \left( {i{Q_{SP}}{\xi _m}y} \right)} 。 $

(8)

其中：$A = \frac{{2{\lambda _0}{{\left( {2\pi } \right)}^3}{\varepsilon ^2}}}{{a{{\left( {\varepsilon + 1} \right)}^2}\left( {\varepsilon - 1} \right)}}\exp \left( {\frac{{ikz}}{{\sqrt {\varepsilon + 1} }}} \right), {\xi _m} = \sqrt {1 - {{\left( {\frac{{2\pi m}}{{a{Q_{SP}}}}} \right)}^2}} $。

可见，在观察场强分布时，在y=nτ处形成Talbot像，与原光栅图样近似相同；在$y = \left( {n + \frac{1}{2}} \right)\tau $处形成$\frac{1}{2}$分数Talbot像，与原光栅图样相比，在横向上平移了半个周期。表明在傍轴近似下，表面等离子体波在金属面上实现了Talbot效应。

3. Talbot效应特性分析 3.1. Talbot图样

由(8) 式可知，关于m的级数求和与自变量z无关，而z只存在于e指数项中。因此，在等离子体—偶极子近似中，Talbot图样与z的取值无关，只有电磁场的绝对强度随着与金属表面距离的增加而呈e指数衰减。

实验选取金属层材质为银(介电常数ε=-130.83+i3.32)，入射光波长为λ=1.55 μm，则激发的表面等离子体波波长λ_SP=1.544 1 μm。根据(8) 式计算z=0.1λ高度处E_z，并用MATLAB编程模拟出各种光栅周期a所对应的表面等离子体波的Talbot图样。

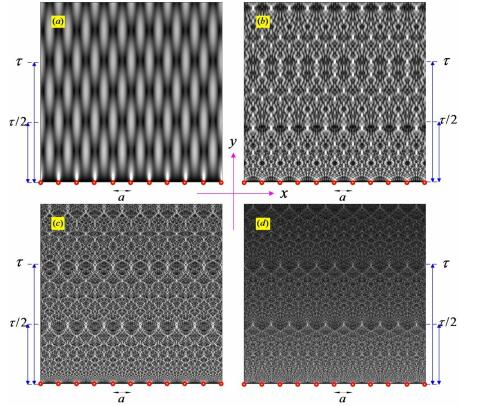
图 4为光沿z轴入射，周期为a的表面等离子体波的Talbot图样。可见，当a=λ_SP时，Talbot效应还没有形成；当a=5λ_SPh时，自成像现象已比较明显，尤其是在$\frac{\tau }{2}$附近的自成像点，强度较大，非常清晰；当a扩大到10λ_SP及20λ_SP时，表面等离子体波展成了非常好的Talbot图样，在y≈τ处，形成了Talbot像，与原光栅图样近似相同；在$y \approx \frac{\tau }{2}$处形成$\frac{1}{2}$数Talbot像，与原光栅图样相比，在横向上平移了半个周期。

3.2. 自成像点的特性分析 3.2.1. $\frac{\tau }{2}$附近的像点

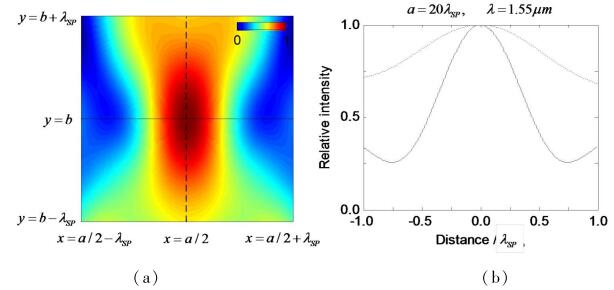
通过(8) 式可计算并模拟出像点，当a=20λ_SP时，在z=0.1λ高度处，$x = \frac{a}{2}, y = \frac{\tau }{2}$附近的场强分布和能量分布特性如图 5所示。图 5(a)表示像点附近的能量分布情况，图 5(b)表示在(a)图中十字交叉线上的相对能量分布。从图中可以看到，像点的横向线宽约为0.5λ_SP，纵向线宽比横向大。当改变光栅周期，或者观察Talbot距离附近的像点时，这种现象依然存在。

3.2.2. 像点位置与小孔周期的关系

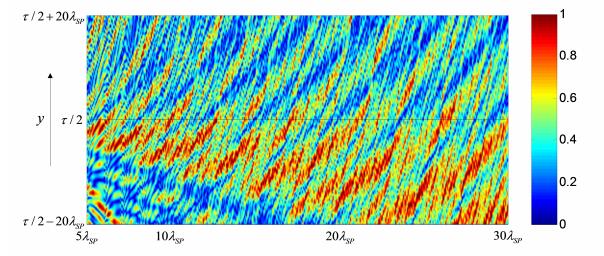
由(8) 式可以得到z=0.1λ高度处，$\left( {x, y} \right) = \left( {\frac{a}{2}, \frac{\tau }{2}} \right)$附近像点的位置与小孔周期关系如图 6所示，图中绘出的是各个小孔周期与空间位置所对应的相对场强。

由图 6可看出，不管光栅周期如何，像点的位置一般都在$y = \frac{\tau }{2}$以下，而且图 6还表明了像点位置会随小孔周期的变化而变化。因此，我们既可以直接通过改变小孔周期来控制成像点位置，又可以通过对光波波长作微小的改变来小范围的改变小孔周期，从而控制成像点的位置。

4. 结语

根据电磁场理论，采用偶极子近似模型分析了金属表面等离子体波的Talbot效应，并用MATLAB模拟出了自成像效应的图形，进一步分析了自成像点的性质、小孔周期变化对Talbot效应的影响以及介电常数变化对表面等离子体波的Talbot效应的影响。由表面等离子体波的Talbot效应出发，进一步验证了金属面上相应的一维准周期结构会实现自成像效应。