2. 陕西省X射线检测与应用研究开发中心,陕西 渭南 714099
2. Center of X-Ray Detection and Application of Shaanxi, Weinan 714099, China
网络技术和人工智能技术的快速发展,在便利民众的同时,也带来了一些负面问题:版权认证的归属问题、交易过程中防篡改复制问题、保护信息媒体数据原创性问题等都成为工业4.0时代下急需解决的问题。数字水印技术作为解决这些问题的一种有效方法,已成为信息安全领域的研究热点。国内数字水印领域专家谭铁牛院士、长江学者杨义先教授等都为数字水印技术在版权保护、防篡改性上作出了重要贡献。但现有的数字水印技术因其自身的局限性,并未在电商和微商时代的背景下取得广泛的实际应用。
目前,零水印技术仍处在探索及发展阶段,2016年12月我们在国外多个大型学术数据库以“zero-watermarking”为主题词进行检索,在2011—2016年间共检索出50篇相关论文,其中Science Direct(elsevier)数据库检索到1篇,Springerlink数据库检索到8篇,SPIE数据库检索到1篇,IEEE Xplore Digital Library数据库检索到3篇,会议论文37篇;国内在中国知网数据库(CNKI)以“零水印”为主题进行检索,共检索出513篇相关学术论文。统计和分析以上研究成果,说明关于零水印的研究在国内处于研究发展阶段,而在国外尚属起步,但该方向的研究已引起相关领域专家、学者的关注。零水印算法的核心是提取能够表征图像本质特性的图像特征信息,然后和版权水印图像绑定生成零水印,最后将零水印在版权认证数据库中(IPR)注册保存。因此有关零水印的研究可以转换为如何有效提取原始宿主图像特征问题。目前研究者在零水印图像特征的构造问题上已提供了很多思路和解决方法,这些方法可以归结为两大类:(1) 基于空间域的零水印图像特征构造方法[1-2];(2) 基于图像变换(变换域)的零水印图像特征构造方法[3-10]。在变换域中,针对旋转几何攻击,本文提出一种基于LPM和双谱分析的抗旋转攻击零数字水印算法,可以有效抵抗旋转造成的几何变换。
1 对数极坐标变换(Log Polar Mapping,LPM)令二维函数I(x, y)表示笛卡儿坐标(直角坐标系)(x, y)上的灰度图像,该灰度图像顺时针旋转φ角度后可以表示为:
| $ {I^r}\left( {x,y} \right) = I\left( {x\cos \varphi + y\sin \varphi ,y\cos \varphi - x\sin \varphi } \right)。$ | (1) |
在笛卡儿坐标系(直角坐标系)下,令:
| $ x = {e^\rho }\cos \theta ,y = {e^\rho }\sin \theta ,0 \le \theta < 2{\rm{\pi ,}}\rho \in {\Re ^2}, $ | (2) |
将(2) 式代入(1) 式得:
| $ \begin{array}{l} {I^r}\left( {{e^\rho }\cos \theta ,{e^\rho }\sin \theta } \right) = I\left( {{e^\rho }\cos \theta \cos \varphi + {e^\rho }\sin \theta \sin \varphi ,{e^\rho }\sin \theta \cos \varphi - {e^\rho }\cos \theta \sin \varphi } \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = I\left( {{e^\rho }\cos \left( {\theta - \varphi } \right),{e^\rho }\sin \left( {\theta - \varphi } \right)} \right)。\end{array} $ | (3) |
简记为:
| $ {I^r}\left( {\rho ,\theta } \right) = I\left( {\rho ,\theta - \varphi } \right)。$ | (4) |
其中:ρ、θ分别表示极轴和极角的采样点的个数(对数极坐标系下的二维坐标)。
由(4) 式可知灰度图像在笛卡儿坐标系(直角坐标系)下若将图像旋转角度φ,则该图像会在对数极坐标系下沿着极角θ方向平移φ个单位。
2 双谱分析定义1 某平稳随机时间序列S(k)的三阶累积量可以表示为:
| $ {L_{SSS}}\left( {m,n} \right) = E\left[ {S\left( k \right) \cdot S\left( {k + n} \right) \cdot S\left( {k + m} \right)} \right], $ | (5) |
则其双谱密度为:
| $ {D_s}\left( {{\omega _1},{\omega _2}} \right) = \sum\limits_m {\sum\limits_n {{L_{SSS}}\left( {m,n} \right)\exp \left[ { - j\left( {m{\omega _1} + n{\omega _2}} \right)} \right]} } 。$ | (6) |
其中:双谱密度Ds(ω1, ω2)一般为复数表示,即它不但有幅度信息,而且包含相应的相位信息,(6) 式又可表示为:
| $ {D_s}\left( {{\omega _1},{\omega _2}} \right) = \left| {{D_s}\left( {{\omega _1},{\omega _2}} \right)} \right|\exp \left[ {j{\varphi _D}\left( {{\omega _1},{\omega _2}} \right)} \right]。$ | (7) |
定义2 假设S(k)是确定性实数随机序列,且时长为有限值,则其傅里叶变换S(ω)存在,则有:
| $ \begin{array}{l} {D_s}\left( {{\omega _1},{\omega _2}} \right) = S\left( {{\omega _1}} \right) \cdot S\left( {{\omega _2}} \right) \cdot {S^ * }\left( {{\omega _1} + {\omega _2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = S\left( {{\omega _1}} \right) \cdot S\left( {{\omega _2}} \right) \cdot {S^ * }\left( { - {\omega _1}\; - {\omega _2}} \right)。\end{array} $ | (8) |
其中:*表示相应复数的共轭。
如果{S(k)}为一零均值高斯随机平稳序列,则对于所有的m和n,有:
| $ {R_s}\left( {m,n} \right) = E\left[ {S\left( k \right)S\left( {k + m} \right)S\left( {k + n} \right)} \right] = 0, $ | (9) |
所以其高斯过程的双谱必然恒定等于0。
3 算法的实现过程 3.1 旋转不变性实现设原始二维图像f(x, y)经LPM后变换为I(ρ, θ),旋转φ后得Ir(ρ, θ),根据(4) 式有:
| $ {I^r}\left( {\rho ,\theta } \right) = I\left( {\rho ,\theta - \varphi } \right)。$ | (10) |
由傅里叶变换的性质可知,Ir(ρ, θ)对应的傅里叶变换的结果可以表示为:
| $ {Z^r}\left( {r,k} \right) = Z\left( {r,k} \right)\exp \left( {i\varphi k} \right)。$ | (11) |
其中:Z(r, k)表示I(ρ, θ)的傅里叶变换的结果,Zr(r, k)表示Ir(ρ, θ)对应的傅里叶变换的结果,将(11) 式代入(8) 式,可得:
| $ \begin{array}{l} D_s^r\left( {r,{\omega _1},{\omega _2}} \right) = {Z^r}\left( {r,{k_1}} \right) \cdot {Z^r}\left( {r,{k_2}} \right) \cdot {Z^r}\left( {r, - {k_1}\;\; - {k_2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = Z\left( {r,{k_1}} \right) \cdot Z\left( {r,{k_2}} \right) \cdot Z\left( {r, - {k_1}\;\; - {k_2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {D_s}\left( {r,{\omega _1},{\omega _2}} \right)。\end{array} $ | (12) |
可见,图像f(x, y)旋转前后其LPM后的双谱具有不变性。
为了降低计算的复杂度,对于LPM后的二维图像矩阵,取其n个列向量,然后对每一列向量组成的双谱绝对值矩阵进行分析,则有:
| $ D_s^r\left( {r,{\omega _1},{\omega _2}} \right) = \left| {{D_s}\left( {r,{\omega _1},{\omega _2}} \right)} \right|,s = 1,2, \cdots ,n。$ |
对n个ri对应的双谱绝对值矩阵分别计算其均值、方差、能量、主对角线元素之和并组合得到对应的特征向量。
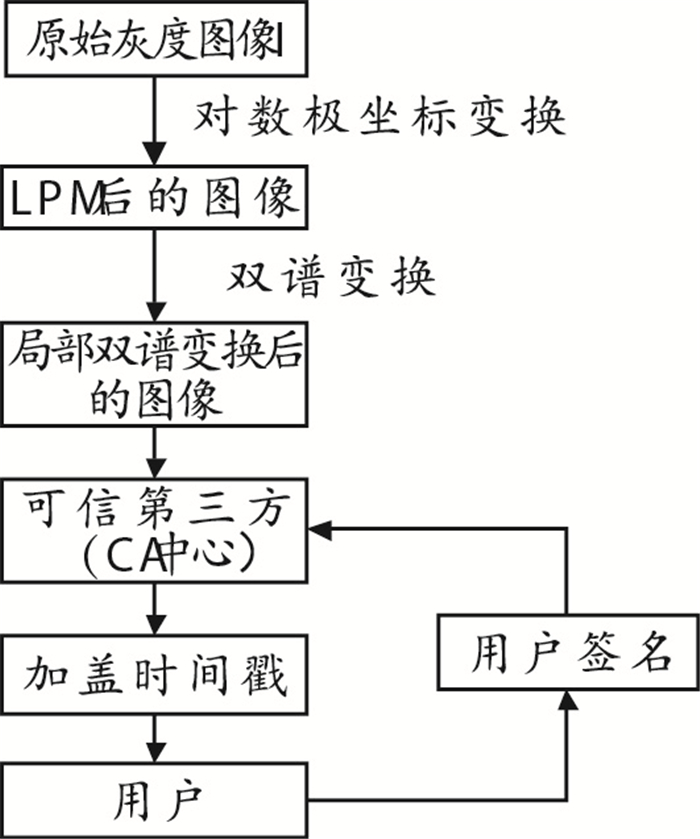
3.2 零数字水印注册具体步骤如下:
步骤1:将笛卡尔坐标系的二维灰度图像通过对数极坐标变换(LPM),得到对数极坐标系下的二维灰度图像矩阵;
步骤2:对对数极坐标系下的二维灰度图像矩阵,提取n列局部矩阵进行双谱变换,得到双谱绝对值矩阵,计算其矩阵的均值、方差、能量、主对角线元素之和并组合得到对应的特征向量(|E1||V2||S3||D4|),将其在版权认证中心进行注册;
步骤3:对特征向量|E1||V2||S3||D4|加盖时间戳,并且连同用户的相关签名信息一并在版权保护中心进行实名注册,此时则宣布原始载体图像已在版权保护之下。
|
图 1 零水印注册流程图 |
|
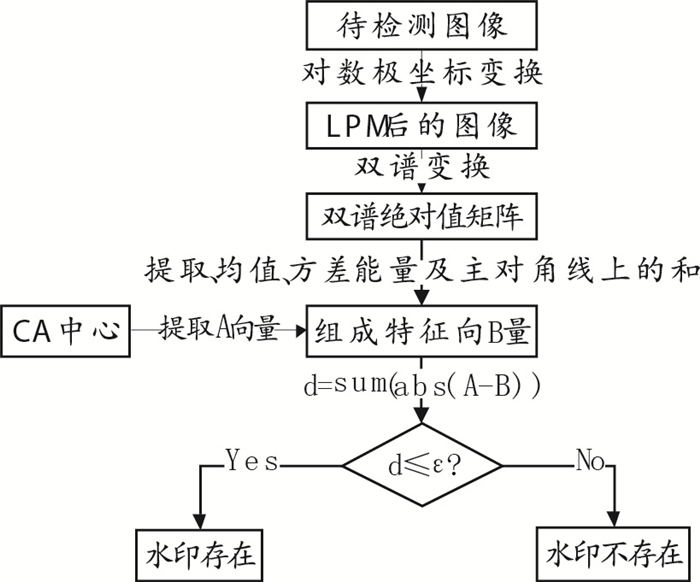
图 2 零数字水印检测流程图 |
具体步骤如下:
步骤1:首先对待检测图像分别进行对数极坐标变换和双谱变换操作,然后计算双谱绝对值矩阵的均值、方差、能量及主对角线上的和,并将最后计算的值作为数字向量B。
步骤2:计算出数字向量B与零数字水印在注册时版权认证中心的数字向量A的绝对差之和:
| $ d = \frac{1}{4}\sum\limits_{i = 1}^4 {\left| {{A_i} - {B_i}} \right|} 。$ | (13) |
当d≥ε,同时时间戳记录的时间与版权保护中心提供的信息不相符时(ε为经验系数,取值为0.05) 则验证结束,说明待检测二维图像中不包含版权水印信息,否则证明版权水印存在。
4 Matlab仿真结果及分析利用Matlab 2013a软件进行仿真实验,二维宿主图像采用256×256的“Lena”灰度图像。图像的视觉质量的客观定量描述采用峰值信噪比PSNR。
| $ MSE = \frac{1}{{MN}}\sum\limits_{x,y} {{{\left( {I\left( {x,y} \right) - {I^1}\left( {x,y} \right)} \right)}^2}} , $ | (14) |
| $ PSNR = 10 \cdot \lg \left( {{{255}^2}/MSE} \right)。$ | (15) |

|
图 3 原始载体图像及其他不同载体图像 |
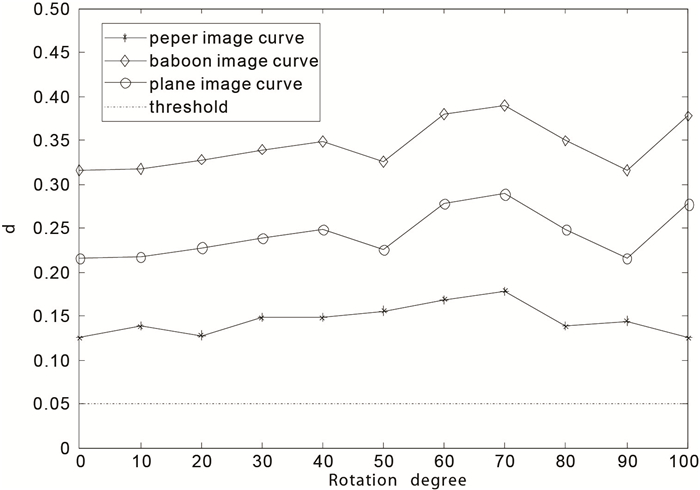
本文进行了以下相关的验证性实验:实验1是二维宿主图像遭受旋转几何变换攻击后的实验,结果如表 1所示;实验2是对Lena二维宿主灰度图像进行JPEG有损压缩操作,再进行水印检测,结果如表 2所示;实验3是Lena二维宿主灰度图像感染高斯噪声及滤波后进行的水印检测,结果如表 3所示;最后对于其他宿主载体图像是否会出现误判(错误检测)的情况,实验4给出了零数字水印误检率结果。分别选取Plane、Pepper和Baboon 3幅二维宿主灰度图像,结果如图 4所示。实验结果表明,本方案对旋转、有损压缩、平滑滤波具有一定的鲁棒性,同时通过误检率实验也可以看出本方案具有很好的检测精度。
| 表 1 原始宿主图像遭受几何攻击后的实验结果 |
| 表 2 有损压缩(JPEG压缩)的实验结果 |
| 表 3 椒盐噪声、高斯噪声及平滑滤波后的分析实验结果 |
|
图 4 不同载体图像的旋转实验误检曲线图 |
本文提出了一种对数极坐标和双谱分析的零数字水印算法,结合Matlab仿真实验结果,说明该方法对不同旋转角度下的水印攻击有很强的稳健性,同时该方法对于感染了椒盐噪声、高斯白噪声、均值和中值滤波、JPEG有损压缩的待检测图像也具有一定的稳健性;最后误检率实验结果也显示了本方法对于没有嵌入数字水印的待检测图像其错误检测的概率也非常小,说明该算法具有很好的检测精度。因此本文所提出的零数字水印是一种较为实用的版权保护方法。
| [1] | 温泉, 孙锬锋, 王树勋. 零水印的概念与应用[J]. 电子学报, 2003, 31(2): 214–216. |
| [2] | 吴伟民, 丁冉, 林志毅, 等. 基于混沌的医学图像篡改定位零水印算法[J]. 计算机应用研究, 2014, 31(12): 3685–3688. DOI:10.3969/j.issn.1001-3695.2014.12.042 |
| [3] | 曲长波, 杨晓陶, 袁铎宁. 小波域视觉密码零水印算法[J]. 中国图像图形学报, 2014, 19(3): 367–371. |
| [4] | 谢勇, 张金龙, 张雯. 一种基于奇异值的抗打印/扫描的彩色图像零水印方案[J]. 包装学报, 2014, 16(3): 11–13. |
| [5] | 马建糊, 何甲兴. 基于小波变换的零水印算法[J]. 中国图像图形学报, 2007, 12(4): 582–585. |
| [6] | 陈伟琦, 李倩. 基于DWT-SVD的图像双零水印算法[J]. 计算机工程与应用, 2014, 36(10): 1992–1996. |
| [7] | 张春凯, 杨德志, 丛佩丽. 基于Krawtchouk矩和NSCT变换的鲁棒性零水印算法[J]. 计算机应用与软件, 2014, 31(3): 282–285. |
| [8] | 冯银波, 陈善学. 基于四元数域的彩色图像双重零水印算法[J]. 计算机应用与软件, 2014, 31(9): 264–267. |
| [9] | 吴伟民, 丁冉, 林志毅, 等. 基于细胞自动机与奇异值分解的零水印算法[J]. 计算机应用, 2014, 34(6): 1690–1693. |
| [10] | 赵玉霞. 基于混沌系统与提升小波的抗剪切攻击的彩色图像盲水印算法[J]. 工程图像学报, 2010, 24(4): 216–219. |
 2017, Vol. 32
2017, Vol. 32