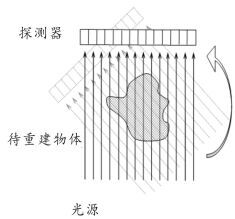
计算机断层成像术CT(Computed Tomography)可以在不破坏样品的情况下,利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像,由此获取样品内部的结构信息。一种典型的二维CT系统如图 1所示(全国大学生数学建模竞赛2017年A题),平行入射的X射线垂直于探测器平面,每个探测器单元看成一个接收点,且等距排列。X射线的发射器和探测器相对位置固定不变,整个发射—接收系统绕某固定的旋转中心逆时针旋转180次。对每一个X射线方向,在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处理后得到180组接收信息。
|
图 1 CT系统示意图 |
CT系统安装时往往存在误差,从而影响成像质量,因此需要对安装好的CT系统进行参数标定,即借助于已知结构的样品(称为模板)标定CT系统的参数,并据此对未知结构的样品进行成像。
请建立相应的数学模型和算法,解决以下问题:
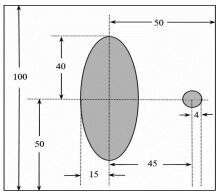
在正方形托盘上放置两个均匀固体介质组成的标定模板,模板的几何信息如图 2所示,相应的数据文件见文献[1]中的附件1,其中每一点的数值反映了该点的吸收强度,这里称为“吸收率”。对应于该模板的接收信息见文献[1]中的附件2。请根据这一模板及其接收信息,确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。[1]
|
图 2 模板示意图(单位:mm) |
针对该问题, 要求计算探测器单元之间的距离,该问题可通过查询CT系统的工作原理,求出探测器吸收强度与探测器单元距离的对应关系,从而求出探测器单元之间的距离,或者根据CT系统中,发射—接收系统中两束射线可穿过固体介质最大直径对应的单元格个数求解出探测器单元之间的距离。
2.2 确定CT系统旋转中心在正方形托盘上的位置针对该问题, 需要确定CT系统旋转中心在正方形托盘上的位置,第一步建立合适的平面直角坐标系,由于在任意方向时,探测器所接收的椭圆和圆的最大吸收强度分别为通过椭圆中心和圆心的射线(如果没有通过中心,可以选择邻近的射线),利用Matlab软件找出最大值及其所在的行和列, 从而可以确定出几种特殊的旋转方向, 进而根据平面几何相关知识求解出CT系统旋转中心在正方形托盘上的位置。
2.3 确定CT系统使用的X射线的180个方向针对该问题,同2.2中所述, 找出某些特殊点的坐标及其旋转角度,首先需要确定X射线的初始入射方向, 根据文献[1]附件2中第一列数据,可以获得X射线的初始入射时探测器的吸收强度,进而查找出一些其他特殊的旋转方向, 从而最终确定出180个旋转方向。
3 模型假设(1) 假设所有的平行光束都照到探测器上,探测器单元等距排列。[2-4]
(2) 旋转载物台为完全水平放置。
(3) 载物台中轴线所确定的平面在平板探测器的某个垂面上。
(4) 平板探测器表面完全平整光滑。
(5) 附件中所给的数据真实可靠。
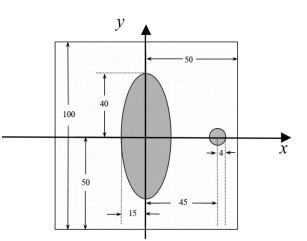
4 模型的建立和求解 4.1 模型准备建立坐标系:以正方形托盘中心为坐标原点O,椭圆的短轴为ox轴,椭圆的长轴为oy轴建立平面直角坐标系, 如图 3所示。
|
图 3 建立直角坐标系(单位:mm) |
在图 3中,假设当X射线与oy轴平行时,通过椭圆左右两侧的X射线对应的探测器[5-6]分别为Ti、Tj,通过圆左右两侧的分别为Tk、Tl,则椭圆所对应探测器个数为n, 圆所对应的探测器个数为m,圆的半径为r,椭圆的长短轴分别为a、b,探测器单元之间的距离为d,因为平行入射的X射线垂直于探测器平面,并且每个探测器单元看成一个接收点,且等距排列,但是由于X射线可能与椭圆或圆不是正好相切的,因此利用椭圆和圆同时计算,然后对其加权平均(权重取为α、β, α+β=1),综上所述可以建立出探测器单元之间的距离模型为:
| $d = \alpha \frac{{2b}}{n} + \beta \frac{{2r}}{m}。$ | (1) |
其中:n=|Ti-Tj|, m=|Tk-Tl|。
利用文献[1]中的附件2中所给的数据进行计算:通过Matlab在附件2的数据中分别求取最大值得到相关的数值为:Ti=277, Tj=169,Tk=430,Tl=402,r=4,a=40, b=15,α=β=$\frac{1}{2}$,代入式(1) 可以解出d=0.28,即探测器单元之间的距离为0.28 mm。
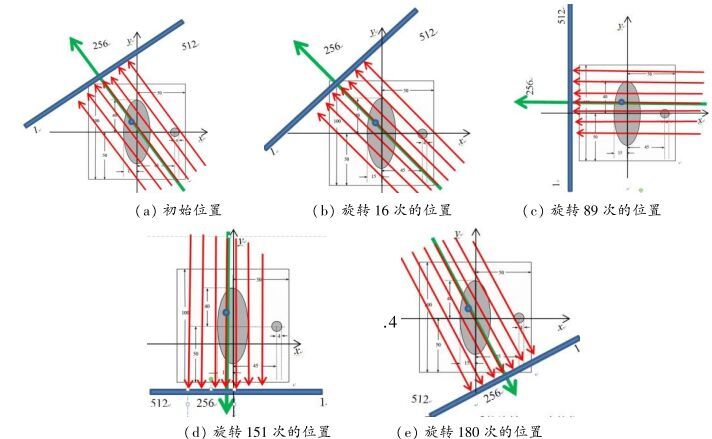
4.3 旋转中心模型在模型准备中的直角坐标系里,假设CT系统旋转中心在正方形托盘中的位置为(x0, y0),假设旋转中心在探测器单元中心对应的X射线T1=256上, 在附件2中找出两种特殊的旋转方向如图 4(c)和图 4(d)所示,假设图 4(c)和图 4(d)中X射线对应的探测单元分别为Ti、Tj,则可以建立旋转中心模型为:
|
图 4 几种特殊的旋转位置 |
| $\left\{ \begin{array}{l} {x_0} = ({T_i} - {T_1})·d,\\ {y_0} = ({T_1} - {T_j})·d。\end{array} \right.$ | (2) |
其中:d为探测器单元之间的距离。
利用附件2中的数据进行计算:Ti=216,Tj=223,d=0.28, 则通过式(2),可以计算出旋转中心坐标为(-9.27, 6.27)。
4.4 旋转方向模型附件2中的数据为512×180二维数字矩阵。共有180列:分别表示该CT发射—接收系统绕固定旋转中心逆时针旋转180次;共有512行:分别表示每次旋转时512个探测单元接收的X射线吸收强度。例如:第一列数据表示CT发射—接收系统初始位置射入X射线所得的吸收强度,数值为0表示X射线未穿过任何介质,直接到达探测器, 数值不为0则表示经过待检测介质吸收后衰减的射线吸收强度。通过Matlab中的最大值函数确定出吸收率最大时所对应的旋转次数, 从而可以得出CT系统在此坐标系中围绕旋转中心旋转的几种特殊的旋转位置,如图 4(a)至图 4(e)。其中:图 4(a)给出了CT系统在坐标系O-xy中的初始位置, 图 4(b)给出了CT系统旋转16次位置, 图 4(c)给出了CT系统旋转89次的位置, 图 4(d)给出了CT系统旋转151次的位置, 图 4(e)给出了CT系统旋转180次的位置。
由图 4(a)可以看出初始位置时X射线是由第四象限射到第二象限, 由图 4(b)可以看出当旋转16次时椭圆和圆介质开始重合, 由图 4(c)可以看出X射线与ox轴平行,方向相反, 由图 4(d)可以看出X射线与oy轴平行,方向相反, 由图 4(e)可以看出旋转180次后正好旋转了180°,X射线是由第二象限射到第四象限。
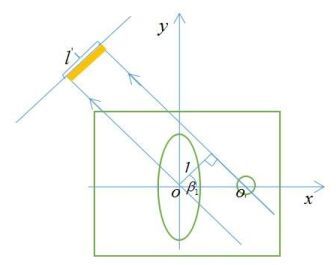
由于在任意方向时,探测器所接收的椭圆和圆的最大吸收强度分别为通过椭圆中心和圆心的射线(如果没有通过中心,可以选择邻近的射线),如图 5所示。
|
图 5 通过中心的X射线 |
对附件2中的数据, 利用Matlab中的最大值函数,查找出每一次旋转过程中探测器所接收的椭圆和圆的最大吸收强度对应的探测器单元,并分别记作Tei、Tci,l表示这两个探测单元之间的距离,每次的旋转角度记为θi,i=1, 2, …, 180(旋转180次),则可以建立旋转方向模型:
| ${\theta _i} = {\beta _i} - {\beta _{i - 1}}。$ | (3) |
其中:βi=arccos$\frac{l}{{l'}}$, l=|Tei-Tci|·d。
这里,βi表示探测器所在直线与ox轴之间的夹角(如图 5所示),初始时β0=0,l′表示椭圆中心和圆心之间的距离,d为探测器相邻单元之间的距离。
利用附件2中的数据进行计算,其中:d=0.28 mm,l′=45 mm,分别计算出一些旋转角度和旋转次数。
(1) 当i=1时,即初始位置时X射线与oy轴之间的夹角θ1,从附件2中第一列容易找出Te1=274,Tc1=416,则l=|Te1-Tc1|·d=40.02,β1=arccos$\frac{l}{{l'}}$=29.64°,则可得出初始位置时X射线与oy轴之间的夹角θ1=β1=29.64°。
同理可以算出,当i=2时, θ2=β2=30.99°。
为了简便计算,假设由第1次到第89次旋转方向均匀,则
| ${\theta _i} = \frac{{90^\circ - 29.64^\circ }}{{89}} = 0.68^\circ ,i = 2,{\rm{ }}3, \ldots ,{\rm{ }}88。$ |
(2) 当i=89时,显然,X射线与oy轴之间的夹角为90°。
为了简便计算,假设由第90次到第151次旋转方向均匀,则
| ${\theta _i} = \frac{{90^\circ }}{{151 - 89}} = 1.64^\circ ,i = 90,91,{\rm{ }} \ldots ,{\rm{ }}150。$ |
(3) 当i=151时,X射线与oy轴之间的夹角显然为180。
为了简便计算,假设由第152次到第180次旋转方向均匀,则
| ${\theta _i} = \frac{{29.64^\circ }}{{180 - 151}} = 1.02^\circ ,i = 152,153,{\rm{ }} \ldots ,{\rm{ }}179。$ |
(4) 当i=180时,X射线与oy轴之间的夹角显然为180°+β1=209.64°。
综上所述,可以给出附件2中的180个旋转方向。
5 结语利用Einstein旋转圆盘几何知识[7]给出了CT系统中探测器单元之间的距离计算方法、旋转中心计算模型、旋转方向模型。数值实验表明,该方法简单易行。
| [1] | 中国工业与应用数学学会. 2017年高教社杯全国大学生数学建模竞赛赛题[DB/OL]. (2017-09-14)[2017-09-15]. 中国大学生在线网站, http://www.mcm.edu.cn/html_cn/node/460baf68ab0ed0e1e557a0c79b1c4648.html. |
| [2] | 李兴东, 杨民, 李德红, 等. 一种改进的三维CT系统射线源焦点投影坐标测量方法[J]. 光学学报, 2011, 31(12): 112–116. |
| [3] | 张聪哲, 李晓苇, 杨昆. 扇束等角型CT与等距型CT的比较研究[J]. CT理论与应用研究, 2013, 22(2): 215–223. |
| [4] | 敖波, 曾亚斌, 吴伟, 等. 等角扇形束投影的CT重建算法研究[J]. 失效分析与预防, 2013, 8(4): 206–211. |
| [5] | 张顺利, 李卫斌, 唐高峰. 滤波反投影图像重建算法研究[J]. 咸阳师范学院学报, 2008, 23(4): 47–49. |
| [6] | 吴梦秋, 程正兴. 反投影重建算法的改进算法[J]. 西安工业学院学报, 2004, 24(1): 76–81. |
| [7] | 韩双明, 白秀英. Einstein旋转圆盘几何性质的研究[J]. 渭南师范学院学报, 2012, 27(12): 46–48. DOI:10.3969/j.issn.1009-5128.2012.12.012 |
 2017, Vol. 32
2017, Vol. 32