水是人类赖以生存的自然资源与物质基础。随着人民生活水平的不断提高,人们对水的需求和对水质量以及水问题的关注程度越来越高,对水的研究也越深入。[1-5]特别是近年来人们对水的固态(冰)结构、物理性质、结构相变、扩散和输运等进行了系统而深入的研究[6],其目的是为更深入地了解水,为人类生存提供安全的、高质量的水。
我国居民生活用水主要来自于地下水(井水)和地表水(江河湖泊水、水库水)这两种形式,水的存在方式和采自区域决定了水质的差异。传统成熟的水质检测分析方法多基于化学技术手段,化学方法会对水样品产生破坏,对环境造成污染,因此,通过物理方法研究水问题,既经济简便,又无污染,而且避免了化学方法带来的种种弊端。物理方法是基于水对力、电、磁、光、超声等产生的物理效应实现对水质的检测研究。伴随着物理方法的运用,人们能更深入地研究水的分子构形、水分子间以及水与物质间的相互作用等理论问题,这些问题在化学、物理学、生物学等方面都具有重要意义。[7-9]理论与实验研究表明,表面张力的变化能够反映液体结构与组分[10-11]、品质[12-13]以及表面、界面等重要信息[2, 14]。故可通过研究水的表面张力,分析其所携带的物理信息,实现对水质的物理检测。另外,水拉曼散射峰相对强度、峰宽、峰位置、峰形状、峰对称性等信息与水分子振动有关,由于水中所含的溶解杂质物对水分子振动有较大影响,通过测试水的拉曼光谱,可以得到水分子振动信息,从中折射出水中溶解的杂质物,因此拉曼散射可用于研究水质。除此之外,同步辐射和中子散射技术、扫描隧道显微镜技术、和频振动光谱技术等新技术相继应用于水问题研究,为人们在分子尺度上理解水提供了全新的技术支持。
1 水分子结构特点水分子是由1个氧原子和2个氢原子组成的简单的三原子分子,化学分子式是H2O。常温、常压下,自由态水分子的O—H键长为0.095 72 nm,H—O—H键角为104.52°,形成“V”型结构,如图 1所示。水分子的“V”型结构与其电子组态有关。组成水分子的氧原子最外层有2个2s电子和4个2p电子,而氢原子只有1个1 s电子,氧原子需要与2个氢原子通过核外电子sp杂化结合形成2个O—H键,O—H键分解能为5.18 eV, 剩下2个未成键的2p电子(称为孤对电子),在水分子与外界发生作用时起着决定性作用。水分子的结构决定了水的性质与功能,水分子是极性很强的极性分子,由于sp杂化,氢原子失去电子,其所在区域(氢原子端)带有较强的正电(正电概率约为+5/11),未成键的2p电子其所在区域(氧原子端)带有较强的负电(正电概率约为-6/11)。[15]由此形成的电极矩从氧原子端沿H—O—H键角平分线穿到氢原子端,单个水分子的电极矩为1.855 D。
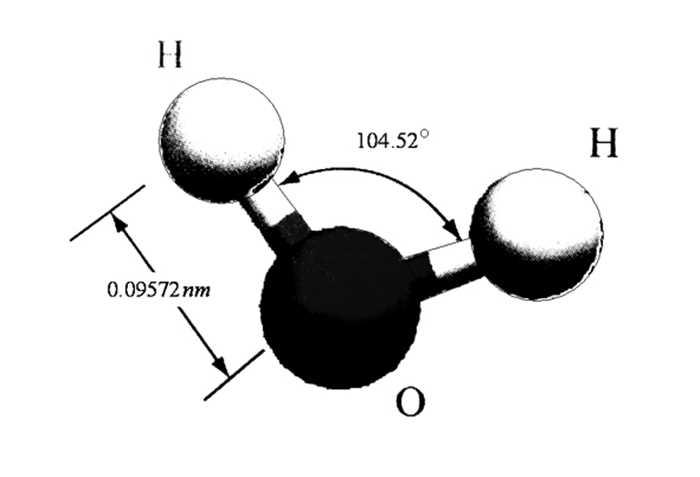
|
图 1 水分子的几何结构 |
自由态水分子有9个自由度,即3个平动自由度、3个转动自由度、3个振动自由度。平动自由度和转动自由度与外界环境关系较大,3个转动自由度对应的转动惯量分别为1.022 0 g-1cm-2、1.918 7 g-1cm-2、2.937 6 g-1cm-2。振动自由度属于水分子内部自由度(振动模式)。图 2表示水分子振动模式,其中伸缩振动是O—H键长改变的振动,根据其反演对称性质分为对称伸缩振动(用ν1表示)和反对称伸缩振动(用ν2表示),弯曲振动是H—O—H键角改变的振动(用ν3表示)。这3种振动模式波数的理论值分别为:ν1=3 657 cm-1,ν2=3 756 cm-1,ν3=1 595 cm-1[16]。外界环境对振动自由度有较大影响。
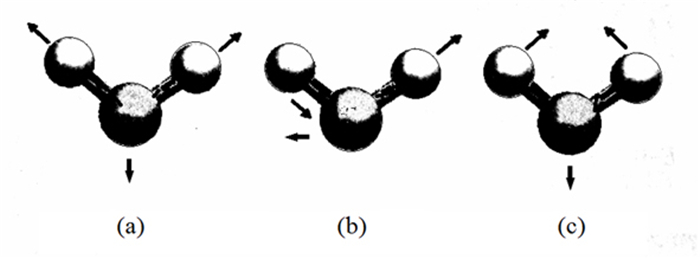
|
图 2 水分子的振动模式 (a)对称伸缩振动;(b)反对称伸缩振动;(c)弯曲振动 |
水分子之间靠着很强的氢键结合,氢键是电负性很强的原子(如氧或氮)和已与氧或氮等共价结合的氢原子之间相互吸引而产生的分子间或分子内相互作用。水分子中的氢原子与另一个最近邻水分子中的氧原子未成键的2p电子相互吸引,形成了键角接近180°、键长约为29.76 nm的O—H…O直线型结构。每个水分子中只有2个未成键的2p电子,它最多只能与2个氢原子形成氢键,加上它本身的2个氢原子又和其最近邻的2个水分子的氧端形成氢键。因此,1个水分子最多能形成4个氢键,这样的5个水分子组成了局域化的完全氢键化的四面体结构(如图 3所示),这是水分子结构的基本特征。在水分子四面体基本结构中,位于四面体中心的水分子被四面体顶角的4个水分子包围着,顶角上的4个水分子又和它们近邻的水分子通过氢键作用相结合。因此,水是由氢键构成的方向性很强的由单水分子、两水分子、三水分子到多水分子相互结合的各种不同大小的缔合态水分子网络团簇结构。[17]
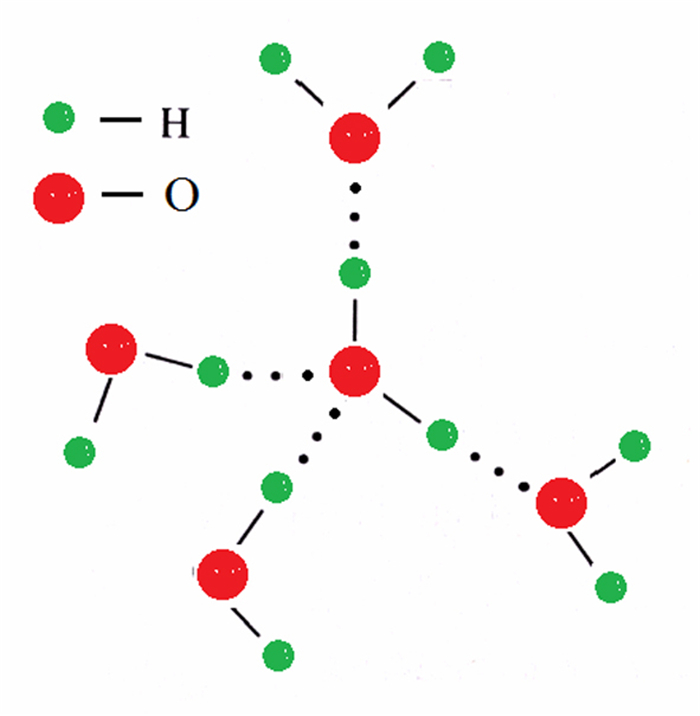
|
图 3 水的五分子四面体结构 |
从分子尺度上理解水,常常还要考虑到水分子中氢原子量子运动产生的影响。在水分子的O—H…O直线型结构中,每个O—O连线上有且仅有1个H,H非常明显的量子效应使得处于2个O间的H的双势阱结构变为单势阱结构。这需要用到全量子化理论方法处理H的量子效应,这一问题的深入研究,是理解水的种种特异性质以及水的各种作用机理的关键。[18]
水分子是多电子体系,它的Schrodinger方程为
| $ H\psi \left( {r,R} \right) = E\psi \left( {r,R} \right)。$ | (1) |
其中:r、R分别表示所有电子和原子核的坐标,哈密顿量H分别由电子动能He、原子核动能HN以及电子与核相互作用能He, N组成,表示为
| $ \begin{array}{l} H = {H_e} + {H_N} + {H_{e,N}}\\ \;\;\;\; = - \sum\limits_k {\frac{{{\hbar ^2}}}{{2{m_e}}}\nabla _k^2} - \sum\limits_j {\frac{{{P^2}}}{{2{M_j}}}} + \frac{1}{2}\sum\limits_{i \ne j} {{V_N}\left( {{R_i} - {R_j}} \right)} + \frac{1}{2}\sum\limits_{k \ne l} {\frac{{{e^2}}}{{\left| {{r_k} - {r_l}} \right|}}} - \sum\limits_{k,j} {\frac{{{Z_n}{e^2}}}{{\left| {{r_k} - {R_j}} \right|}}} 。\end{array} $ | (2) |
由于电子质量远小于原子核,应用Born-Oppenheimer近似,把核运动和电子分离开来。
电子的Shrodinger方程为
| $ \left[ { - \sum\limits_k {\frac{{{\hbar ^2}}}{{2{m_e}}}\nabla _k^2} + \frac{1}{2}\sum\limits_{k \ne l} {\frac{{{e^2}}}{{\left| {{r_k} - {r_l}} \right|}}} - \sum\limits_{k,j} {\frac{{{Z_n}{e^2}}}{{\left| {{r_k} - {R_j}} \right|}}} } \right]\psi \left( r \right) = E\psi \left( r \right)。$ | (3) |
若完全忽略电子—电子相互作用,电子波函数可以表示为单电子波函数的乘积形式
| $ \psi \left( r \right) = {\varphi _1}\left( {{r_1}} \right){\varphi _2}\left( {{r_2}} \right) \cdots {\varphi _n}\left( {{r_n}} \right)。$ | (4) |
代入(3) 式化为单电子的Hartree方程
| $ \left[ { - \frac{{{\hbar ^2}}}{{2{m_e}}}{\nabla ^2} + V\left( r \right) + \sum\limits_{j\left( { \ne i} \right)} {\int {{\rm{d}}r'\frac{{{{\left| {{\varphi _j}\left( {r'} \right)} \right|}^2}}}{{\left| {r - r'} \right|}}} } } \right]{\varphi _i}\left( r \right) = {E_i}{\varphi _i}\left( r \right)。$ | (5) |
其中:V(r)是体系中原子核的库仑势。考虑到电子自旋为ħ/2,其波函数交换反对称,用单电子波函数的Slater行列式代替多电子体系波函数,就得到了Hartree-Fock方程
| $ \left[ { - \frac{{{\hbar ^2}}}{{2{m_e}}}{\nabla ^2} + V\left( r \right) + \sum\limits_{j\left( { \ne i} \right)} {\int {{\rm{d}}r'\frac{{{{\left| {{\varphi _j}\left( {r'} \right)} \right|}^2}}}{{\left| {r - r'} \right|}}} } } \right]{\varphi _i}\left( r \right) - \sum\limits_{j\left( { \ne i} \right)} {\int {{\rm{d}}r'\frac{{\varphi _j^ * \left( {r'} \right){\varphi _i}\left( {r'} \right)}}{{\left| {r - r'} \right|}}{\varphi _j}\left( r \right) = } } {E_i}{\varphi _i}\left( r \right)。$ | (6) |
使用Hartree-Fock方程,考虑到电子关联效应带来的微扰修正后,可以对单个水分子或水的团簇进行精确计算。
2 水表面张力及测量水的结构特点决定了水的性质。物质两相的分界面是两相(汽—液、液—液、汽—固、液—固)之间的过渡区域,汽液两相的分界面与液相蒸发和汽相凝结等相变过程密切相关。处于汽液界面层(表面相)中的分子的内外两侧分子受到不同的作用力,同相分子的引力作用发生在内侧分子间,异相分子的引力作用发生在外侧分子间,内侧分子间的作用大于外侧分子间的作用,故表面层内分子所受的合力指向液体内部。表面相分子所受到的这种非对称分子间的作用即为表面张力。水是自然界最普遍的物质,它与外界相互作用是通过“表面”分子中氧原子的2个未成键的2p电子实现的,水的重要作用也是通过“表面”完成的。特别是扫描隧道显微镜问世之后,人们可以在亚分子尺度下观察水分子的吸附行为,以及液态水的表面与界面行为,揭示了水分子的吸附作用源于未配对的孤对电子和氢键作用的本质。
外力拉伸液体形成液膜,使液体表面积增大,在这个过程中外力所做的功在数值上等于液体界面分子与内部分子的势能差,也等于恒温与恒压条件下液体吉布斯自由能的增量。吉布斯自由能的增量在数值上等于液体的表面张力,表面自由能随温度变化的关系为
| $ \frac{{\partial \sigma }}{{\partial T}} = \frac{{\partial \gamma }}{{\partial T}} < 0。$ | (7) |
其中:γ是比表面自由能,σ是表面张力。(7) 式说明了液体表面张力随温度变化的关系。
平衡状态下液体的液面是平面,当外界对液体进行扰动时,在液体浅表层内形成了向四周传播的表面张力波。表面张力波在液体中的传播速度为[19]
| $ \left\{ \begin{array}{l} {V_x} = A\omega {e^{kz}}\sin \left( {kx - \omega t} \right),\\ {V_z} = - A\omega {e^{kz}}\cos \left( {kx - \omega t} \right)。\end{array} \right. $ | (8) |
其中:A是波振幅,ω是角频率,k是波矢,坐标z正方向垂直液体表面指向液体外侧,坐标x(y)方向沿液体表面,Vz、Vx分别是沿z、x方向的波速。(8) 式表明表面张力波随透入液体深度z的增加而指数形式地快速衰减,当z→-∞时,Vz→0,Vx→0。因此,液体表面张力波是液体浅表层分子受外界扰动产生的,并且在液体浅表层内沿液体表面(xoy面)传播。在短波且忽略重力因素影响的情况下,表面张力波的波长和频率之间的关系为[20]
| $ {v^2} = \frac{{8{{\rm{\pi }}^3}\sigma }}{{\rho \lambda _s^3}}。$ | (9) |
其中:σ是表面张力,ν是表面波频率,λs是表面波波长。(9) 式说明表面波频率越高则相应的波长越小。
G.Weisbuck认为[21],液体表面张力波可以作为一种反射型光栅,光栅常数d等于表面张力波的波长λs,测量衍射条纹信息,由光栅方程求出光栅常数d,代入(9) 式求得液体表面张力。表面波频率ν与振源频率非常接近,实际计算中表面波频率ν取为振源频率[22]。液体表面张力波对激光衍射形成的衍射条纹的光强分布为[23]
| $ I\left( \theta \right) = RL\sum {J_n^2\left( {4\pi A\cos \frac{\theta }{{{\lambda _L}}}} \right)\sin {c^2}\left( {\frac{{{\lambda _s}}}{{{\lambda _L}}}\theta - \frac{n}{{\cos \varphi }}} \right)} 。$ | (10) |
其中:R和L分别是表面波波面对光的反射系数和有效反射宽度,
根据文献[10-15]的研究结论,液体表面张力与液体结构、组分、品质、表面和界面等信息有关,测量液体表面张力可以定性地说明液体中的组分。自然状态下,水中溶解了各种杂质,使水富含的各种元素离子对水的表面张力产生较大影响,它们填充在水分子间,其中带正电荷的金属离子和水分子的氧端作用,带负电荷的非金属离子和水分子氢端作用,使水分子团簇结构发生改变。气液两相分子的物理环境存在差异,表层分子间距离大于内部分子间距离,导致表层分子间作用力增大。理论分析表明[24],水分子在离子型杂质周围定向排列,这些定向排列的水分子微观结构发生变化,表面张力也发生变化。
本实验用拉脱法和激光衍射法分别测试了蒸馏水、自来水、水库水等水样品的表面张力。蒸馏水制备于渭南师范学院化学实验室,自来水采自渭南市某居民家中,水库水采自渭南市生产生活用水供给的沋河水库。
拉脱法使用复旦天欣科教FD-NST-1型液体表面张力系数测定仪,图 4是表面张力系数测定仪的力敏传感器定标拟合直线,线性相关系数为0.999 85,力敏传感器的灵敏度为2.888 0 V/N。激光衍射法用音频信号发生器作为振动源(频率为200 Hz)在水样品表面激发一正弦表面波,从He-Ne激光器(λL=632.8 nm)发出的激光照射表面波形成衍射条纹。图 5是蒸馏水表面张力波产生的激光衍射花样照相图,图 5表明水表面张力波形成了非常好的衍射效果。
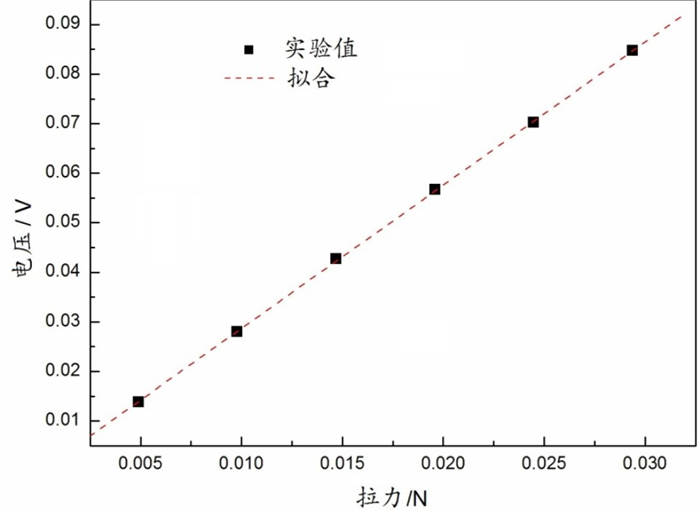
|
图 4 力敏传感器定标拟合图 |

|
图 5 蒸馏水表面波产生的激光衍射花样照相图 (室温20℃,He-Ne激光,频率200 Hz) |
水库水和自来水中均含有丰富的矿物质,这些矿物质以阳离子形式存在于水中。为了说明了水表面张力随金属(阳)离子浓度的变化,首先测试了不同浓度的氯化钠(化学纯)水溶液在室温时的表面张力(如图 6所示),结果表明氯化钠水溶液的表面张力随氯化钠浓度(质量百分比)增加而增大。
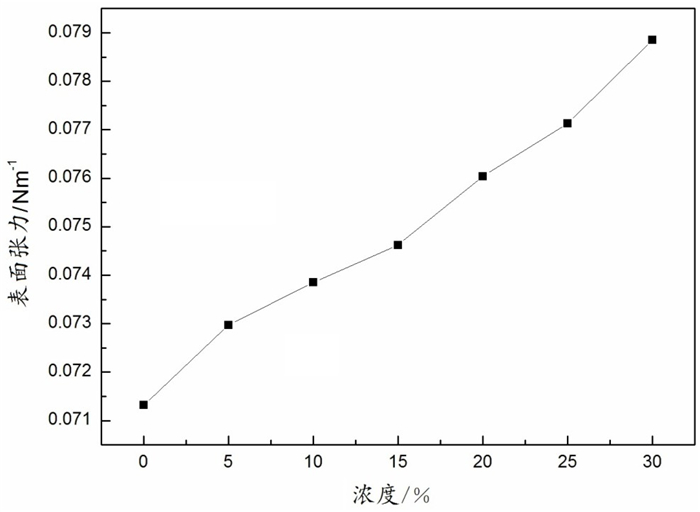
|
图 6 不同浓度的NaCl水溶液的表面张力 |
图 7是拉脱法和激光衍射法测量的蒸馏水、水库水、自来水的表面张力随温度的变化关系。图 7表明水表面张力随温度增加线性减小,这符合热力学理论分析的结果。水是由大量氢键形成的动态团簇,它们随着温度变化处于涨落之中,温度上升,水分子平均动能增大,弱化了氢键作用,使表面张力减小[25]。从图 7还可以看出两种方法的差异:其一,相同温度点同一样品的表面张力,拉脱法的结果较接近于理论值。激光衍射法是一种动态测定方法,该方法通过机械振源在水表面振动产生向四周传播的表面波,激光束射向水表面,形成了衍射条纹,这个方法的测量结果受液体界面汽相影响较大。拉脱法属于机械式的静态测定方法,使拉脱法的拉环(金属铝环)接触平静的水面,水分子中氧原子的孤对电子通过静电引力吸附于拉环上,提升拉环当静电引力与水表层分子间的引力平衡时,力敏传感器上可得到水的表面张力,该方法的测量结果几乎不受液体界面汽相影响。其二,蒸馏水表面张力值比理论值小,自来水和水库水的表面张力都大于蒸馏水值和理论值。这是由于自来水和水库水中富含具有促进水分子团簇缔合作用的杂质离子,以及其他可溶性杂质物。
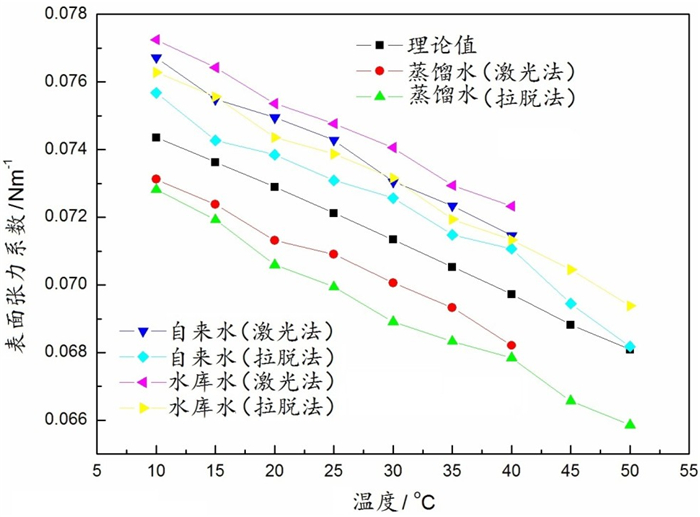
|
图 7 拉脱法和激光衍射法测量水表面张力 |
两种测量方法的物理机制不同,测量结果虽然也存在一定差异,但都得到了与热力学理论一致的结果,说明了水表面张力随温度增加而减小。因此通过测量水表面张力可以定性地反映水质,由于水中溶解物的复杂性,其和表面张力的定量关系是需要进一步研究的问题。
3 水拉曼散射拉曼散射是光和物质相互作用的重要现象。物质处于永不停息的运动中,物质的拉曼散射折射出组成物质的分子的振动和转动能级的信息,这些振动和转动能级具有拉曼活性,它们分别对应着拉曼散射中特定的光谱线(拉曼频移)和峰相对强度。拉曼频移反映的是组成物质分子的原子间相对位移信息和受力情况,说明原子结合成分子化学键的强弱。拉曼散射相对强度说明了分子极化率对简正振动模的微分值贡献的大小,决定于分子中电荷受到原子核的束缚程度。拉曼散射峰宽、峰形状的对称性等与物质纯度有关。因此,指认物质拉曼散射的频移、峰相对强度、峰宽、峰形状对称性等信息,可以确定组成物质的分子结构信息和溶解在物质中杂质离子(分子)对物质分子结构的影响。[26]
理论和实验研究表明,由于水分子氢键振动驰豫时间和转动驰豫时间接近于拉曼散射的特征时间[27],因此拉曼散射技术是研究水分子结构的技术手段之一。水分子中和氢键作用直接相关的是拉曼活性最强的O—H键伸缩振动,它们由水分子简正振动引起分子极化率的强弱,即由水分子拉曼活性的大小决定,因此水分子振动模式的拉曼光谱技术研究多集中在O—H键伸缩峰区域[28]。O—H键对称伸缩振动致使水氢键作用最强,导致水分子的极化率变化最大,拉曼活性最强,其波数位于3 600 cm-1附近且最容易被观测到;O—H键弯曲振动引起水分子的极化率变化相对较小,拉曼活性相对于对称伸缩振动较弱,其拉曼峰在波数1 600 cm-1附近出现,但峰强度远小于对称伸缩振动;O—H键反对称伸缩振动引起水分子的极化率变化极小,它的拉曼活性最弱且不容易被观测到。本实验使用Renishaw公司inVia型激光拉曼光谱仪(激光波长514 nm,输出功率≥40 mW,扫描范围1 000 cm-1~4 000 cm-1)测试样品的室温拉曼光谱。
图 8是水以及相同浓度(5%)的氯化钾和氯化钠溶液室温拉曼光谱。图 8中出现了属于对称伸缩振动的波数在3 600 cm-1附近的拉曼峰,属于弯曲振动的波数在1 600 cm-1附近的拉曼峰,反对称伸缩振动的拉曼峰没有出现。对称伸缩振动拉曼峰的相对强度为:水>氯化钠>氯化钾,由于氯化钾和氯化钠溶液中Na+、K+以及Cl-的作用,拉曼峰对称伸缩振动相对强度减小,同时又由于K+半径大于Na+,使拉曼峰对称伸缩振动相对强度进一步减小了。另外,氯化钾、氯化钠溶液拉曼光谱峰形和水拉曼光谱峰形几乎一致,说明低浓度对拉曼峰形的影响不大。
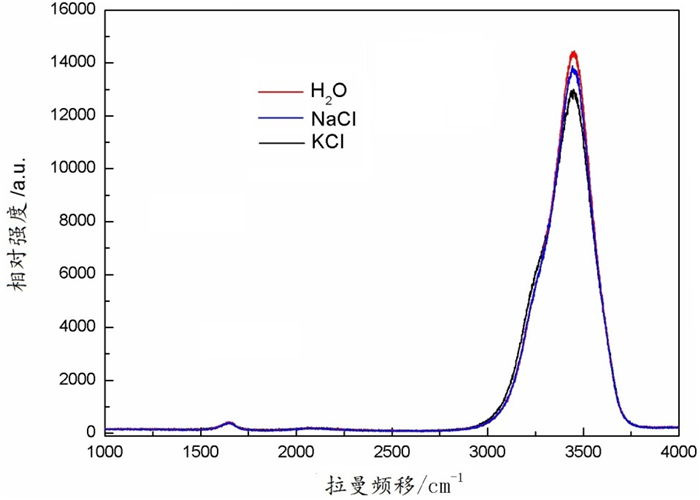
|
图 8 水、5%KCl、5%NaCl溶液室温拉曼光谱 |
图 9是不同浓度氯化钠溶液的室温拉曼光谱。图 9中出现了属于对称伸缩振动(3 600 cm-1附近)的拉曼峰,属于弯曲振动(1 600 cm-1附近)的拉曼峰,没有出现反对称伸缩振动的拉曼峰,表 1是样品室温拉曼散射信息。图 9和表 1拉曼散射信息表明,拉曼峰相对强度和半高宽都有随氯化钠浓度增加而减小的趋势,拉曼峰频移有随浓度增大而变大的趋势,这些信息说明了水中杂质离子浓度对拉曼散射的影响。氯化钠溶解过程中,作用于NaCl分子的力使其化学键断裂,形成独立的Na+和Cl-。溶解之后离子—水之间的作用加强了,Cl-周围O原子半径发生了变化,而H原子的分布半径几乎不变。[16]微观上可能是导致拉曼峰强度变化和拉曼峰位置移动的主要原因。水分子热运动使水结构复杂多变,同时也导致了极为复杂的水分子局域模效应,从而使水分子振动态能量统计涨落。[29]因此,从水分子热运动看,统计涨落导致的局域模效应引起了氢键变化,同时离子—水之间的作用,使水四面体网络团簇结构力场改变引起了拉曼峰强度变化与拉曼峰位置移动。
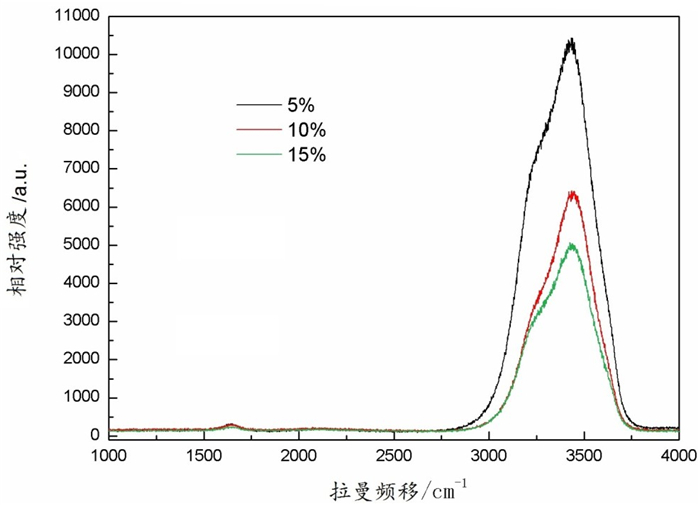
|
图 9 不同浓度Nac1溶液室温拉曼光谱 |
| 表 1 不同浓度氯化钠溶液室温拉曼散射对称伸缩振动 |
图 10是蒸馏水、自来水和水库水的室温(20℃)拉曼光谱,图 10中出现属于对称伸缩振动的拉曼峰和属于弯曲振动(小图是弯曲振动的局部放大)的拉曼峰,同样没有出现反对称伸缩振动拉曼峰。表 2是样品室温拉曼散射信息,峰相对强度、半高宽的大小为:蒸馏水>自来水>水库水;拉曼频移大小为:蒸馏水 < 自来水 < 水库水。比较图 9和图 10,图 9样品中只含Na+和Cl-,且离子浓度大于图 10样品。图 10样品中离子种类远比图 9丰富,不但有一价阳离子,而且还存在二价阳离子以及其他阴离子,它们共同影响拉曼散射。又由于这些离子含量(浓度)很小,它们对拉曼散射的影响也相对较小。两图的拉曼光谱较为相似,图 9与图 10和表 1与表 2均说明了拉曼散射的峰相对强度、峰宽和峰频移等与水中溶解物含量相关。
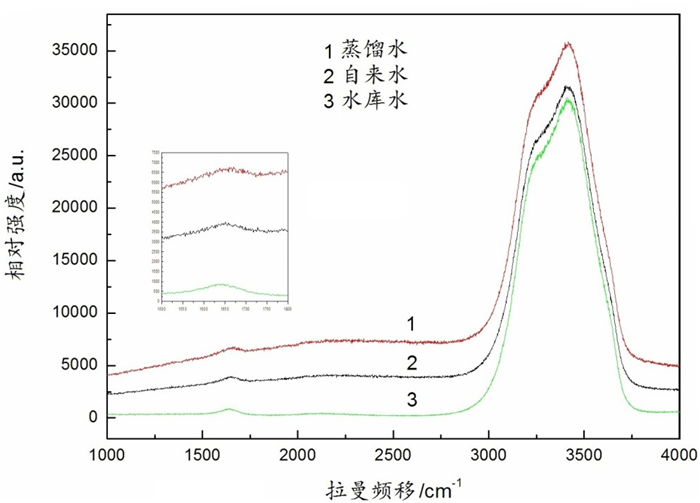
|
图 10 蒸馏水、自来水、水库水室温拉曼光谱 |
| 表 2 蒸馏水、自来水、水库水室温拉曼散射对称伸缩振动 |
普通水中存在氢键未被破坏的水分子以及与水中杂质离子相互作用使氢键弱化或被破坏的两类水分子,他们透射出的拉曼散射信息不同于纯水的拉曼散射信息。自来水和水库水中富含的大量可溶杂质物带有正、负电荷离子,它们分别与水分子的氧、氢端作用,破坏或弱化了氢键的作用,并且伴随着溶解杂质物浓度的增加,氢键被破坏或弱化的也就越多,是导致水拉曼谱峰变窄的重要原因。[30]陈勇等人研究了不同盐离子对水分子拉曼效应的影响,他们认为水中溶解物浓度是影响拉曼频移、峰形状、峰相对强度等的因素,溶液盐浓度越大,峰相对强度越小,拉曼峰不对称性越明显。[31]图 10中样品的拉曼信息说明了水库水溶解的杂质物最多,蒸馏水最少,这些杂质物的存在使得水结构变得更加复杂。
自来水中存在的大量带正电的金属阳离子(钾、钠、钙、镁等)以及带负电的其他阴离子是影响水拉曼峰强度的一个重要因素,这些荷电离子具有较强的局域电场,其周围的水分子密度发生了大幅度的统计涨落。水分子有很强的极性和较大的电极化率,溶解于水中的这些荷电离子与水分子相互作用,改变了水分子团簇结构,使水分子极化率减弱,振动能量降低,拉曼峰强度减小。实验样品中,经过技术处理提纯的蒸馏水的杂质物浓度非常低,对拉曼峰相对强度的影响最小。水处理工艺滤掉了对人体健康有害的重金属离子和其他溶解物以及保留了利于人体健康的金属离子的自来水,其拉曼峰强度受这些离子的影响相对较小。自然状态下的水库水中杂质离子含量相对最大,离子种类较多,这些杂质离子对拉曼峰强度的影响也最大。实验结果显示出的信息与文献[24]和[30]的结论基本一致。另外,杂质元素离子半径、荷电量等因素对氢键也产生一定的弱化作用,影响拉曼谱的峰形状、相对强度、峰宽等信息。[32]本实验水样品的拉曼峰形状基本相似,但峰形的对称性、峰宽、相对强度等存在明显差异,表明杂质离子种类和含量是影响水结构以及拉曼散射的主要因素。
4 结语拉脱法和激光衍射法测定的蒸馏水、自来水和水库水的表面张力的结果定性地表明了水中杂质含量对水表面张力的影响。两种方法分别属于机械式的静态方法和动态方法,结果表明了水表面张力随杂质物浓度的增加而增大,随温度升高而减小,与热力学理论完全符合。激光衍射法受液面汽相影响较大,同样条件下拉脱法几乎不受液面汽相影响,因此拉脱法的测试结果更接近于理论值。在相同温度点,水库水的表面张力最大,自来水次之,蒸馏水最小。水中杂质离子与水分子相互作用,弱化或破坏了水分子氢键作用,强化了水团簇缔合结构,导致表面层分子间作用力增大,其宏观表现为表面张力增大。
水拉曼光谱的对称伸缩振动拉曼峰相对强度、半高宽、拉曼频移、峰形对称性等都与水中杂质离子浓度有关,表现为对称伸缩振动拉曼峰的相对强度、半高宽都有随着水中杂质物浓度的增加而减小的趋势,而拉曼频移有随着水中杂质物浓度的增加而增大的趋势。水以及相同浓度氯化钾和氯化钠溶液室温拉曼光谱说明了不同杂质离子对拉曼光谱的对称伸缩振动拉曼峰有影响。而不同浓度的氯化钠溶液的拉曼散射表明了水中杂质离子浓度对拉曼散射的影响。水样品拉曼散射的结果为:峰相对强度、半高宽的大小为:蒸馏水 > 自来水 > 水库水;拉曼频移大小为:蒸馏水 < 自来水 < 水库水。水样品的拉曼散射峰形基本相似,但拉曼峰相对强度、半高宽、拉曼频移、峰形对称性等存在差异,这些差异源于水中杂质离子的种类及其含量。杂质离子都带有一定荷电量,它们产生的局域电场以及与水分子偶极作用产生的统计涨落导致的局域模效应引起的氢键变化以及水分子的振动,改变着水团簇结构,使水分子极化率降低,表现为拉曼散射的差异。
| [1] | 顿珠次仁, 严志宏, 达瓦潘多, 等. 水的多分子簇结构及改变团簇结构方法的研究进展[J]. 中央民族大学学报(自然科学版), 2014, 23(1): 27–32. |
| [2] | 涂育松, 方海平. 液态水微观结构研究的新进展[J]. 物理, 2010, 39(2): 79–84. |
| [3] | 李如忠. 水质评价理论模式研究进展及趋势分析[J]. 合肥工业大学学报(自然科学版), 2005, 28(4): 369–373. |
| [4] | 蔡然, 杨宏伟, 和劲松, 等. 液态水氢键结构的拉曼光谱研究进展[J]. 化工环保, 2010, 30(6): 492–495. |
| [5] | 刘松红, 庞成群, 冯俊杰, 等. 水分子振动体系动力学研究[J]. 宁夏大学学报(自然科学版), 2012, 33(3): 243–246. |
| [6] | 张瑶, 李照兵, 张鑫, 等. 水分子在Bi(111) 表面上的吸附和自组装[J]. 中国科学:化学, 2016, 46(4): 389–393. |
| [7] | 张晓峻, 董婉佳, 孙露, 等. 水的光学特性实验研究[J]. 实验技术与管理, 2014, 31(3): 43–50. |
| [8] | erdaguer A V, Sacha G M, luhm H B, et al. Molecular Structure of Water at Interfaces:Wetting at the Nanometer Scale[J]. Chemical Reviews, 2006, 106(4): 1478–1510. DOI:10.1021/cr040376l |
| [9] | Errington J R, Debenedetti P G. Relationship between structural order and the anomalies of liquid water[J]. Nature, 2001, 409: 318–339. DOI:10.1038/35053024 |
| [10] | 李艳琴, 张宏剑. 不同种类杂质对液体表面张力系数的影响[J]. 实验室研究与探索, 2013, 32(4): 43–46. |
| [11] | 文军, 李芳菊. 基于表面张力和拉曼光谱的水质检测与分析[J]. 西华大学学报(自然科学版), 2016, 35(3): 66–70. |
| [12] | 景晨娟, 刘亚龙, 曹旭东. 利用表面张力系数和黏滞系数检测牛奶品质初探[J]. 西北农林科技大学学报(自然科学版), 2012, 40(5): 205–208. |
| [13] | 陈佰树, 王畅, 张平, 等. 基于力敏传感器的牛奶掺水量的检测研究[J]. 高师理科学刊, 2013, 33(1): 34–37. |
| [14] | 张克武, 张宇英. 分子热力学前沿基础研究中的新理论13:论纯质的微观结构与液体表面张力理论计算法[J]. 黑龙江大学自然科学学报, 2007, 24(4): 435–440. |
| [15] | 濮培民, 濮江平, 朱政宾. 水分子结构模式及液态固态水若干特征成因探讨[J]. 气象科学, 2016, 36(5): 567–580. DOI:10.3969/2016jms.0046 |
| [16] | 孟胜, 王恩哥. 水基础科学理论与实验[M]. 北京: 北京大学出版社, 2014: 225. |
| [17] | Wiggins P M. High and low density water in gels[J]. Progress in Polymer Science, 1995, 20(6): 1121–1163. DOI:10.1016/0079-6700(95)00015-8 |
| [18] | Tuckerman M E, Marx D, Klein M L, et al. On the quantum nature of the shared proton in hydrogen bonds[J]. Science, 1997, 275: 817–820. DOI:10.1126/science.275.5301.817 |
| [19] | 文军, 李芳菊. 基于表面张力的水质检测与分析[J]. 实验室研究与探索, 2015, 34(4): 37–40. |
| [20] | 邱吉尔, 王莹. 激光衍射法测量液体表面波的波长并确定其属性[J]. 大学物理实验, 2013, 26(3): 4–5. |
| [21] | 王文华, 赵林, 闫波. 离子对水结构的影响[J]. 化学通报, 2010(6): 491–498. |
| [22] | 鄢锐. 液体表面波理论及其频率特性[D]. 西安: 陕西师范大学硕士学位论文, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10718-2009046236.htm |
| [23] | 李芳菊. 液体表面张力系数的激光衍射测量法[J]. 渭南师范学院学报, 2013, 28(9): 30–32. |
| [24] | 周健, 陆小华, 王延儒, 等. 不同温度下水的分子动力学模拟[J]. 计算机与应用化学, 1999, 16(4): 241–244. |
| [25] | Weisbuch G, Garrbay F. Light scattering by surface tension waves[J]. Am.J.Phys, 1979, 47(4): 355–356. DOI:10.1119/1.11821 |
| [26] | 杨序纲, 吴琪琳. 拉曼光谱的分析与应用[M]. 北京: 国防工业出版社, 2008: 255. |
| [27] | Lawrence C P, Skinner J L. Vibrational spectroscopy of HOD in liquid D2O Ⅲ.spectral diffusion, and hydrogen-bonding and rotational dynamics[J]. J.Phys.Che, 2003, 118(1): 264–272. DOI:10.1063/1.1525802 |
| [28] | 李睿华, 蒋展鹏, 师绍琪, 等. 拉曼光谱研究CaCl2和MnCl2对水结构的影响[J]. 物理化学学报, 2003, 19(2): 154–157. |
| [29] | 李远军. 水分子振动态的局域模效应[J]. 四川师范大学学报(自然科学版), 1997, 20(1): 56–60. |
| [30] | 邹受忠, 陈燕霞, 田中群. 不同电解质体系水的拉曼谱的研究[J]. 物理化学学报, 1996, 12(2): 130–135. |
| [31] | 陈勇, 周瑶琪, 查明, 等. 实验研究不同盐离子对水分子拉曼效应的影响[J]. 地球化学, 2008, 37(1): 22–26. |
| [32] | Burikov S A, Dolenko T A, Velikotnyi P A, et al. The effest of hydration of ions of inorganic salts on the shape of the raman stretching band of water[J]. Mol.Spect, 2005, 98(2): 269–273. |
 2017, Vol. 32
2017, Vol. 32