在云环境中,受网络拥堵、随机中断、资源限制等因素的影响,致使云服务在执行过程中用户获得实际QoS与云服务提供商和用户之间的服务质量等级协议(Service Level Agreement,SLA)相违背,造成SLA违例,这一方面影响用户对云服务的使用,另一方面云服务提供商需要向用户赔偿一定的违约金,无疑增加了云服务提供商的成本。所以连续地监测云服务执行过程,尽早预测QoS违例的云服务,可有效避免或减轻其带来的影响,对于保护用户和云服务提供商利益都是至关重要的。[1-4]基于以上分析,首先,本文提出了一种新的云服务QoS预测方法,利用概率模型对被监控工作流实施QoS违例预测。在该方法中,为了防止状态参数过多,利用运行着的服务实例的特征参数进行分析。在QoS预测中,对监测的正在运行服务实例抽取特征参数值,以此为依据,实施对下一阶段要运行服务出现SLA违例的概率进行估算,得出量化的QoS可靠性估算值。其次,借鉴方法论中循环风险管理框架,提出了QoS违例量化赔偿方法,并针对云服务的业务价值设计了开放的、具有广泛性风险的响应方法。
1、云服务QoS预测 (1.1) 云服务质量约束规范的定义为了有效识别组合服务QoS属性的SLA违例,针对QoS属性,本文定义了基于线性时间的时序逻辑区间的QC (质量约束)规范。利用定义的基于QC的操作检测QoS属性的KPI (关键性能指标)[5]。
定义1(QC) QC是对于KPI (关键性能指标)的布尔判定条件。
对于QC (质量约束)定义了3个时序操作:along,within,prec (φ)。
P along T:在属于时间区间T的任意时刻,P为真。
P within T:至少存在某个时刻i∈T,P为真。
prec (φ):该操作符能够接受时序逻辑表达式φ为操作数,利用CEP工具估算prec (φ)。
along是对于区间T的全局线性时序逻辑约束操作符,而within是对于区间T的最终线性时序逻辑约束操作符。将要执行的某状态下某时刻的KPI概率时序表达式用φ表示,prec (φ)为概率是否成立逻辑判断。
(1.2) 云服务QoS队列模型在本文中KPI (关键性能指标)主要指可量化的服务性能指标(如资源利用情况、被请求的服务数等)。在此利用M/M/1队列模型预测组合服务中未执行的组件服务KPI。到达的可用服务请求满足泊松分布,到达率为λ。服务时间遵循均值为μ的指数分布。
设变量k表示单个KPI,k∈Vk=Av∪Cv∪Iv。Av为可允许值集合,当k在该集合中时,当前系统在该状态下,所有定义在该KPI的QC完全满足。Cv为临界值集合,当k在该集合中时,当前系统在该状态下仍能满足最低质量要求。Iv为不可允许值集合,当k在该集合中时,当前系统在该状态下至少有一项已经不能满足服务质量要求的约束值(即QC)。假设Vk满足全序关系并且它的子集不相交,则有任意的a, b, c:a∈Av, b∈Cv, c∈Iv,满足a < b < c。
2、业务相关的服务风险评估利用云服务QoS预测机制检测到服务处于非稳态时,启动违例预警,调整将要运行的服务避免违例或减轻违例的影响。然而当违反了SLA约定QoS违例不可避免发生时,应具有完整风险评估方案,对出现的风险有效应对。通过风险评估提高云服务满足需求的能力,降低云服务提供商的经营风险。下面提出对于单个服务风险的评估。
(2.1) 补偿策略制定当QoS违例发生了,云服务提供商对违约行为进行补偿或赔偿。支付罚金是一种常见的赔偿手段。它也是影响云服务风险的一个重要因素。而补偿策略是指将罚金表示为基于服务环境参数的函数。当服务失败出现并持续时间t,罚金表示为p,则对于单个服务而言p=f(t),且为凸函数。下面针对不同环境给出补偿策略,即罚金补偿函数定义:
(1)连续性云服务补偿策略。连续性云服务是指该服务必须连续执行不可中断。即使很短暂的中断也会引发服务失败。如短暂通信连接或者实时流量控制的敏感数据,即使瞬时中断或者快速恢复都无法弥补这类服务失效[6]。对于该类云服务,它的补偿罚金与服务中断时间t无关,所以其罚金补偿函数为:
| $ {p_{lianxu}} = {\rm{const}}{\rm{。}} $ | (1) |
(2)时距不可用补偿策略。时距不可用是指罚金在一个时距内并不是恒定的,它和服务不可操作t时间成比例。该类补偿通常面对执行持续较长时间的服务,如文件传输、邮件传输等服务,所以其罚金补偿函数与不可操作t时间之间表示为:
| $ {p_{shijin}} = {w_i}t。 $ | (2) |
(3)综合补偿策略。上面两种补偿可能会同时出现在同一服务执行过程中,该服务不可操作时间小于SLA协定时距时,补偿被认为与中断时间t无关,认为t=0。当超过时距时,认为和时间成比例。在此种情况下罚金补偿函数为:
| $ {p_{zonghe}} = {w_i}\left( {t + {\rm{const}}} \right)。 $ | (3) |
(4)非线性补偿策略。罚金补偿函数并不一定总是和时间呈线性关系。如文献[7]中涉及的“雪球效应”,它就是一个典型的非线性函数,表示罚金和服务失效累积时间。这种补偿针对的服务特征为:相对持续时间较短携带有重要或敏感信息且能容忍短时间的服务中断。通常提前如预约服务或具有严格响应时间通信服务具有这些特征。这种“雪球”式的非线性平滑罚金补偿函数为:
| $ {p_{xueqin}} = \frac{{{w_i}}}{{{\rm{const}}}}{t^2}。 $ | (4) |
根据罚金补偿函数可以得到在给定时区不同环境下的补偿策略,但在已知时区的给定补偿策略中罚金价值仍旧是一个随机值,并不是量化的确定价值。设ξ为在某时区内罚金等级,若Pξ(x)=Pr{ξ≤x}表示ξ的累积分布函数,则VaRη代表给定信任等级η下罚金最大值为:
| $ {\rm{Va}}{{\rm{R}}_\eta } = \inf \left\{ {x;\Pr \left\{ {\xi \le x} \right\} \ge \eta } \right\} = P_\xi ^{ - 1}\left( \eta \right)。 $ | (5) |
通过VaRη获得单个服务风险价值,但是在当前网络环境中为了更好地满足用户需求,更多情况是将原来多个单个服务组合成新服务提供给用户。对于云服务组合后的风险价值并不能简单地将单个服务风险价值累加获得,因为VaRη是不具有次加性的。
下面从云服务生存的不可靠的网络环境出发,研究带给组合云服务的风险及其评估策略。对于云服务不可靠网络环境在此用图结构表示(V, E),其中:V表示网络中节点集合,E表示连接网络节点的链路集合。所有这些元素都是不可靠的,都存在失败和修复的可能。因此对于每个不可靠元素联合考虑如下两方面的概率分布函数:(1)失败间隔时间;(2)服务中断时间。在某段时间需要确定单个网络元素c的失败率λc和修复率μc,c∈(V∪E),每个元素失败和修复过程都是独立的。组合云服务风险评估算法通过下面几个步骤完成:
(1)为了得到准确的风险模型,首先需要根据赔偿策略获得每个云服务的罚金;
(2)构建每个服务罚金的连续时间的马尔可夫链,并利用该马尔可夫链获得所有服务相关补偿政策下的聚合罚金价值的均值和方差;
(3)获取通过均值和方差的参数化聚合罚金全概率分布,在这两个分布中,其中一个呈椭圆分布,该分布与对数正态分布最佳拟合。最后根据获得风险全分布,得到包括风险价值VaR在内的分位数。
为了计算VaR等分位数实施风险评估,根据组件云服务罚金,估算给定时区的罚金全概率分布函数。但是各组件云服务罚金是相关的,单个组件服务失败会影响其他组件执行。
首先设X=[X1, …, Xd, …]为随机向量,表示单个组件服务d的罚金,则
| $ {p_{total}} = \sum\limits_d {{X_d}} 。 $ | (6) |
我们用Nd(t)表示服务d在观测时区t中中断的次数,用pd表示单个服务d的单次服务中断的罚金。每一个服务的罚金是多个中断独立罚金的随机总和。假设Nd(t)和pd已知,则在时区t中单个服务d总罚金的均值为:
| $ E\left[ {{X_d}} \right] = E\left[ {{N_d}\left( t \right)} \right]E\left[ {{p_d}} \right]。 $ | (7) |
方差为:
| $ {D^2}\left[ {{X_d}} \right] = E\left[ {{N_d}\left( t \right)} \right]{D^2}\left[ {{p_d}} \right] + {E^2}\left[ {{p_d}} \right]{D^2}\left[ {{N_d}\left( t \right)} \right]。 $ | (8) |
在本实验方案中,假设平衡范围为800 MW,则[minb=-400, maxb=400]。首先针对大小不同规模服务模型估算其在QoS预测阶段花费的时间。在表 1中,第一列给出了队列长度,反映了不同规模的服务,第二列和第三列不同大小服务表示不同规模服务的状态数和变迁数。根据服务的状态数和变迁数,利用CEP等工具,得到第四列QoS预测阶段花费的时间,在前面介绍的队列模型中,该时间应该符合指数分布。从实际测量的第四列数据特征可以看出,它恰好符合指数分布。另外,最后一行数据服务规模非常大,状态数和变迁数都超过了百万,但是实际QoS预测时间为563.831 s,这个速度和智能电网更新速度匹配,所以使用该模型能做到较好的服务质量预测,对可能出现的SLA违例能给出及时的预报。
| 表 1 队列长度、服务大小、花费时间一览表 |
下面选择了队列长度为40的服务,从另一个角度对本文提出的预测模型进行测试。引发平衡变化的队列生率和灭率基本单元值为20 MW。可允许最小值admmin=-200,可允许最大值admmax=200,临界最小值crimin=-380,临界最大值crimax=380。针对第二种QoS的约束条件:prec (ρ=?[F≤30“违例状态”])≤0.05 within 30 m,进行如下3种测试:
测试1:电力生产商输入电网的电力与电力用户需求平衡;
测试2:电力用户需求是电力生产商输入电网电力的2倍;
测试3:电力生产商输入电网的电力超过了电力用户需求。
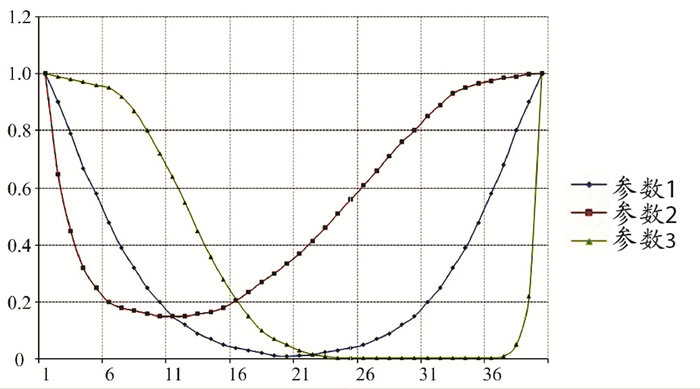
图 2给出了3种不同测试方案下的违例概率。在第一种测试方案中,通过图 1看出违例概率在平衡点双侧均匀对称分布,这和需求平衡现实相吻合。在第二种测试方案中,最小违例概率高于其他两种情况。在第三种测试方案中,所有生产过剩状态都具有较高违例概率,而在过载状态时却拥有较低违例概率。
|
图 1 违例概率分布(队列长度=40) |
|
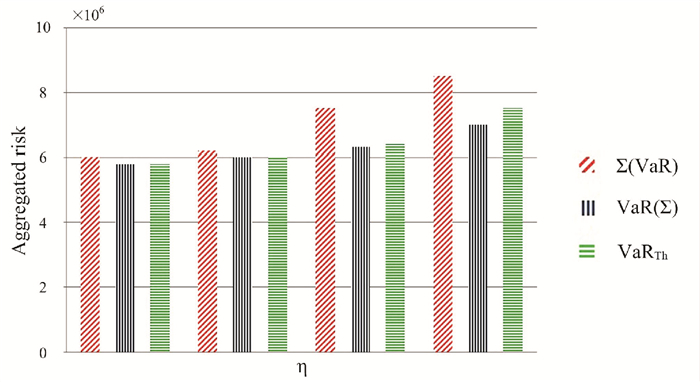
图 2 网络NGe中VaRTh,VaR (Σ),∑(VaR)比较 |
在本测试中选择Weibull分布特征建模失效时间,同时提供指数分布的启发式选择与之对应。Weibull分布在正常运行时间被表示成指数分布。利用两个简单的ON-OFF系统模拟组合云服务。第一个正常运行时间为Weibull分布,中断时间为指数分布(该系统仍称为Weib),第二个全部为指数分布(该系统称为Exp),Weibull分布可以被表示成指数分布:
| $ {m_{Weib}} + \alpha {\sigma _{Weib}} = {m_{Exp}} + \alpha {\sigma _{Exp}}。 $ |
其中:mWeib、mExp表示两个系统在tmax时段期望风险价值;而ασWeib、ασExp表示标准差。设α=1.2时能准确地表示总罚金上界,对所有服务经过计算参数为罚金对数正态分布后,设分位数η=0.9, 0.95, 0.99, 0.999四个等级,每个组合服务中包含10个组件服务,补偿策略为FixedRestart。计算VaRTh(表示组合云服务罚金上界)、VaR (Σ)(表示组合云服务总罚金)、∑(VaR)(组件服务VaR之和)。结果如图 2所示。
根据图 2对比结果可知:即使VaR不具有次可加性,但是将组件单个VaR求和获得的∑(VaR)比组合服务最坏情况总风险上界值还要悲观。而它比VaR (Σ)高出近10%。这表明∑(VaR)并不能准确反映组合服务聚合风险。相较而言,VaRTh和VaR (Σ)差距在0.10%。由此可见,利用上界值可以准确估算出总罚金风险价值,而且无需使用所有补偿策略中的大量服务仿真测试,节约了工作量,具有较高效率。
4、结论本文首先提出一种有效的服务质量预测模型,利用概率模型定量和定性的分析技术,实现了对云环境中SLA违例预测。在本模型中使用参数化的QoS模型(KPI)完成了概率化模型监测分析,以此估算未执行的服务QoS关键指标。利用这种QoS预警机制,能对服务提供商服务质量监控,尽可能地避免服务违例。然而当违例不可避免发生了,接着给出了一套完整风险评估方案,对出现风险有效应对。通过风险评估提高云服务满足需求的能力,降低云服务提供商的经营风险。
| [1] | Pacheco-Sanchez S, Casale G, Scotney B, et al.Markovian Workload Characterization for QoS Prediction in the Cloud[C]//Proceeding of 2011 IEEE 4th International Conference on Cloud Computing. Washington, DC:IEEE, 2011.147-154. |
| [2] | Islam S, Keung J, Lee K, et al. Empirical prediction models for adaptive resource provisioning in the cloud[J]. Future Generation Computer Systems, 2012, 28: 155–162. DOI:10.1016/j.future.2011.05.027 |
| [3] | Leitner P, Wetzstein B, Rosenberg F, et al. Runtime Prediction of Service Level Agreement Violations for Composite Services[C]//Service-Oriented Computing. Berlin:Springer, 2010.176-186. |
| [4] | Leitner P, Michlmayr A, Rosenberg F, et al. Monitoring, Prediction and Prevention of SLA Violations in Composite Services[C]//Proceeding of 2010 IEEE International Conference on Web Services. Miami, FL:IEEE, 2010.369-376. |
| [5] | Cardellini V, Casalicchio E, Grassi V, et al. Qos-driven runtime adaptation of service oriented architectures[C]//Proceedings of the the 7th joint meeting of the European software engineering conference and the ACM SIGSOFT symposium on The foundations of software engineering. New York:ACM, 2009.131-140. |
| [6] | 林凡.面向服务的云计算系统风险评测模型研究[D].厦门:厦门大学硕士学位论文, 2013. http://dspace.xmu.edu.cn/handle/2288/79404?show=full |
| [7] | Franke U. Optimal IT service availability:shorter outages, or fewer?[J]. IEEE Trans. Netw. Serv. Manag, 2012, 9(1): 22–23. DOI:10.1109/TNSM.2011.110811.110122 |
 2016, Vol. 31
2016, Vol. 31