2. 北京应用物理与计算数学研究所,北京 100094
2. Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
在航空、航天、大气、海洋、兵器与国防等重大工程高端领域以及汽车、机械、船舶、电子、土木工程等产品设计应用领域,数值模拟和工程仿真软件已成为理论研究、工程设计与事故分析的重要工具。模拟与仿真不仅可以与理论、实验相互印证,更重要的是模拟与仿真能给出大量没有理论与实验的预测结果。这些预测反映了人们对客观世界规律性的认识,数值模拟的重要价值恰恰体现在对未知世界的预测。这就从逻辑上要求人们回答一系列问题,如何评价数值模拟结果的准确程度?如何评估数值模拟结果的不确定性?特别是那些物理数学理论难以解释、试验难以再现或只有通过巨大耗资才能解决的系统可靠性验证、性能评估和事故原因分析等问题,通过数值模拟与工程仿真可以真实、全过程、全时空、反复精密地进行,以填补理论缺陷和不能做实验的遗憾。[1-2]
基于试验是研究物理机理、机制、事件过程的直接研究方法,但由于多物理过程本身的复杂性,设计科学试验再现物理真实过程是很具挑战性的难题,甚至是不可能的。加之开展科学试验的成本与投入是非常昂贵的,开展大量的试验很不现实。基于数值模拟与工程仿真研究具有成本低、速度快、数据完备且可以模拟各种不同的工况等特点,是一种能模拟真实条件且无危害的间接研究手段。但由于实际物理过程的复杂性和人们认识的缺陷,模拟与仿真中采用的物理模型、计算方法不可避免地有近似、简化或人为因素,使得数值模拟结果的可信性与工程仿真过程的真实性成为人们质疑的重要问题。验证、确认和不确定度量化(Verification and Validation and Uncertainty Quantification,V&V&UQ)是结合物理试验和数值模拟与工程仿真两种研究方法的优点、发展高可信度数值模拟与工程仿真软件的最佳途径。[3-5]
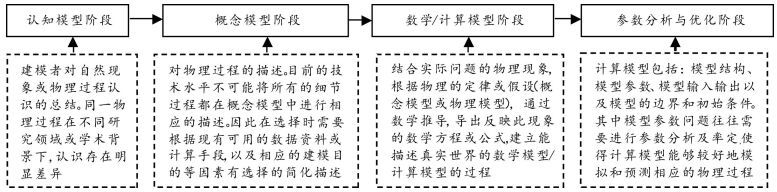
1 计算流体力学建模与模拟中误差与不确定度 1.1 物理建模—物理模型物理建模过程涉及认知模型阶段、概念模型阶段、数学/计算模型阶段、参数分析与优化阶段(如图 1所示)。在物理建模过程中,由于现实世界的复杂性和人们认知的局限性,物理建模过程采用了简化与抽象,使得物理模型的背后有许多误差和不确定性,[6]这些都会影响计算结果的可信度。
|
图 1 物理建模过程 |
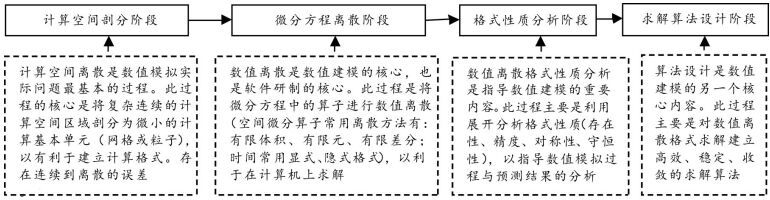
数值建模过程涉及计算空间剖分、微分方程离散、格式基本理论分析和求解算法设计等过程(如图 2所示)。[7]在此过程中由于从连续到离散,存在离散误差、模型初边值条件误差、计算机舍入误差等,对模拟结果会产生很大影响。
|
图 2 数值建模过程 |
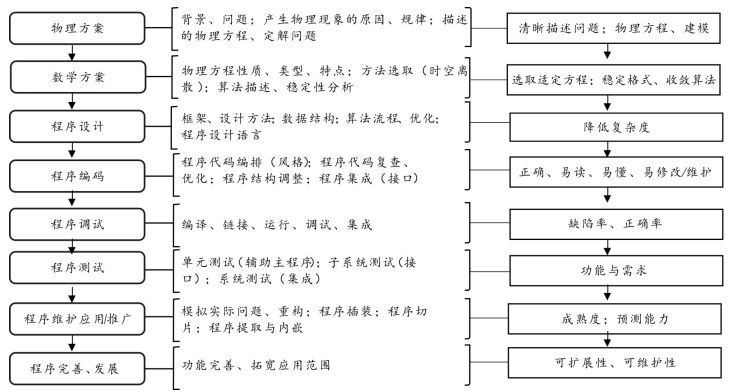
软件研制过程涉及物理方案、数学方案、概要设计、详细设计、编码、测试与考核、应用与维护等软件生命周期的各个要素(如图 3所示)。软件版本、覆盖性测试、各阶段实施文档正确性等,会影响模拟结果的可信度。
|
图 3 程序研制过程 |
问题试验过程涉及几何建模、网格生成、施加初边值条件、模型计算机分析、结果可视化等环节(如图 4所示)。此过程由于不可能精确建模和逼真模拟,模拟与预测结果始终存在误差和不确定性等,影响模拟结果的可信度。

|
图 4 问题模拟过程 |
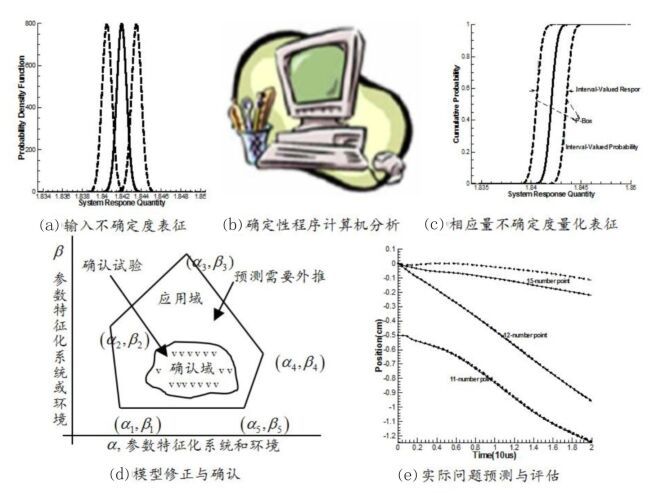
结果分析过程涉及模型输入误差与不确定性表征、模型确定性程序计算机分析、输出(响应量)不确定性量化、计算模型修正或确认、实际问题预测与评估等过程(如图 5所示)。[8-11]此过程由于模型中参数、形式与逼近方法的不确定性,可能会产生与实验不一致的随机结果,对决策产生影响,必须对其进行评估。
|
图 5 结果分析过程 |
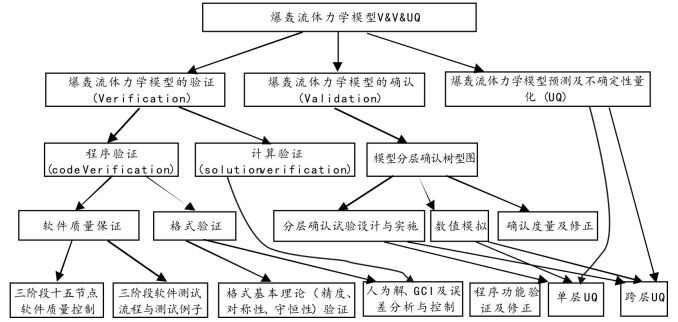
炸药爆轰过程的数学物理模型是双曲型的偏微分方程组与一阶常微分方程、复杂函数关系式耦合在一起的非线性偏微分方程组。[6]图 6给出了爆轰流体力学模拟过程实施V&V&UQ的策略。[12]
|
图 6 爆轰流体力学模型验证、确认与不确定度量化策略 |
爆轰流体力学模拟中误差有两种[13]:一种是对物理问题进行数学描述时因假设和近似而带来的误差,称为建模误差δSM;另一种是数学方程的数值求解带来的误差,称为数值误差δSN。因此模拟误差δS的表达式为:
| ${\delta _S} = S - T = {\delta _{SM}} + {\delta _{SN}}。$ | (1) |
其中:S表示模拟结果,T表示真值或约定真值。
用USM表示对应于建模误差δSM的不确定度,USN表示对应于数值误差δSN的不确定度,则模拟误差的不确定度US可由式(2) 计算:
| $U_S^2 = U_{SM}^2 + U_{SN}^2。$ | (2) |
误差可以被估计,用上角标带*号表示估计值,则:
| ${\delta _{SN}} = \delta _{SN}^* + {\varepsilon _{SN}} = T + {\delta _{SM}} + {\varepsilon _{SN}}。$ | (3) |
其中:δSN*表示对数值误差δSN的估计值, εSN表示对数值误差δSN估计过程中的误差。
利用估计值对模拟结果进行校正,校正后的模拟值SC(数值基准)可定义为:
| ${S_C} = S - \delta _{SN}^*。$ | (4) |
校正后的模拟误差δSC为:
| ${\delta _{{S_C}}} = {S_C} - T = {\delta _{SM}} + {\varepsilon _{SN}}。$ | (5) |
对应的不确定性为:
| $U_{{S_C}}^2 = U_{SM}^2 + U_{{S_C}N}^2。$ | (6) |
其中:USCN为εSN的不确定度估计。
验证过程的核心就是分析模拟中的数值误差并在预测中加以控制。数值误差δSN主要包括迭代误差δI、舍入误差δR、截断误差δT和因其他参数的引入造成的误差δP,即
| ${\delta _{SN}} = {\delta _I} + {\delta _R} + {\delta _T} + {\delta _P}。$ | (7) |
因舍入误差δR在数值误差中所占比例很小,可以忽略不计;模拟中引用的参数一般来源于经过精度测量的参数,取值精度也比较高,故因参数引入造成的误差δP也很小。这样数值误差δSN主要包括迭代误差和截断误差,即
| ${\delta _{SN}} = {\delta _I} + {\delta _T}。$ | (8) |
相应的不确定度为:
| $U_{SN}^2 = U_I^2 + U_T^2。$ | (9) |
其中:UI、UT分别为迭代不确定度和截断不确定度。
同样,数值误差的估计值δSN*也可以表示为:
| $\delta _{SN}^* = \delta _I^* + \delta _T^*。$ | (10) |
其中:δI*和δT*分别为迭代误差和截断误差的估计值。
根据式(4) (5) (10),校正后的模拟值和校正后的数值不确定度就可以分别表示为:
| ${S_C} = S - ( \delta _I^* + \delta _T^*) = T + {\delta _{SM}}^* + {\varepsilon _{SN}},$ | (11) |
| $U_{{S_C}N}^2 = U_{{I_C}}^2 + U_{{T_C}}^2。$ | (12) |
其中:UIC和UTC分别为校正后的迭代不确定度和校正后的截断不确定度。式(11) 可以写为:
| $S = {S_C} + ( \delta _I^* + \delta _T^*)。$ | (13) |
从式(11) 还可以看出,SC等于真值T加上建模误差δSM,再加上假定的数值误差的估计误差εSN,而一般εSN很小,所以SC也可以称为模拟的基准值。
因为截断误差一般是根据几套尺度不同网格上的模拟值来分析的,即截断误差的分析要用到模拟值,而该模拟值不应包含迭代误差,因此在进行截断误差分析之前,首先要分析迭代误差,并利用迭代误差对模拟值进行校正,然后利用校正后的模拟值来推断截断误差。迭代误差对模拟值校正:
| ${\hat S} = S - \delta _I^*。$ | (14) |
一般选取3套网格进行截断误差分析,几套网格间的细化比r可以为常数,也可以为变量,一般取r为常数,因为这样既不影响分析结果,还能使分析简化。
所谓迭代误差,是指由数值计算所得出的当前解与在同一套网格上离散方程的精确解之间的偏差,亦即迭代终止时离散方程的解与精确解的偏差。由于离散方程采用迭代方法求解时不可能绝对满足收敛性,必须在一定的条件下满足后停止迭代。迭代收敛包括一致迭代收敛、振荡迭代收敛和混合迭代收敛。
(1) 对振荡迭代收敛,认为其迭代误差等于0,即
| $ \delta _I^* = 0。$ | (15) |
不确定度为:
| $U = \left| {\frac{1}{2}({S_U} - {S_L})} \right|。$ | (16) |
其中:SU和SL分别为停止迭代时最后一个迭代周期中解的最大值和最小值,可以认为是该不确定度在95%的置信度下的扩展不确定度。
式(15) 是根据振荡迭代收敛的特点,近似认为振荡收敛的迭代误差为随机误差,随着振荡不断进行,模拟值围绕一个确定的值上下波动,故认为其误差为0。同时认为式(16) 所确定的不确定度具有95%的置信度。[14]
(2) 对于一致迭代收敛,可以采用指数方程的曲线拟合法来估计迭代不确定度UIC(95%的置信度)、迭代误差的估计值δI*和校正后的迭代不确定度UIC(95%的置信度),即
| ${U_I} = \left| {S - C{F_\infty }} \right|。$ | (17) |
其中:CF∞为拟合的指数方程当自变量趋于无穷时的函数值。
| $ \delta _I^* = S - C{F_\infty },$ | (18) |
| ${U_{{I_C}}} = 0。$ | (19) |
(3) 对于振荡迭代和一致迭代混合的情况,解的振幅随迭代次数增加而减小。用解的范围来定义第i次迭代中的最大值SU和最小值SL,从而估计迭代不确定度UI(从式(16) 可计算95%的置信度)、迭代误差的估计值δI*和校正后的迭代不确定度UIC(95%的置信度),即
| $ \delta _I^* = S - \frac{1}{2}({S_U} - {S_{{I_C}}}),$ | (20) |
| ${U_{{I_C}}} = 0。$ | (21) |
在进行误差分析前,首先需要判断随网格加密解的变化趋势。设3套网格上对应的用迭代误差校正过的解分别为${\hat S}$1,${\hat S}$2,${\hat S}$3,其中:${\hat S}$1代表尺度最小即网格最密的解;${\hat S}$3代表尺度最大即网格最疏的解。不同网格下模拟值之差用ε表示,即
| ${\varepsilon _{21}} = \hat S_2 - {{\hat S}_1},$ | (22) |
| ${{\hat S}_{32}} = {{\hat S}_3} - {{\hat S}_2},$ | (23) |
| $R = \frac{{{\varepsilon _{21}}}}{{{\varepsilon _{32}}}}。$ | (24) |
其中:下标21表示网格2和网格1之间的值,下标32表示网格3和网格2之间的值。根据不同的R值,可以判断解随着网格加密存在3种变化趋势:
(1) 当0 < R < 1时,表明随着网格的加密数值解沿下凹曲线(曲线斜率绝对值逐渐变小)单调趋近于收敛值,属单调收敛;
(2) 当-1 < R < 0时,表明随着网格的加密数值解在收敛值附近上下振荡,属于振荡收敛;
(3) 当R>1或R < -1时,表明随着网格的加密数值解沿上凸曲线(曲线斜率绝对值逐渐变大)变化或者振荡发散,说明发散或解随着网格加密尚未达到稳定,对这种情况,应进一步加密网格,直到出现(1) 或(2) 的情况。
对于点参数,可能会遇到ε21和ε32都为0的情况,这时可以采用L2范数进行定义,即
| $\left\langle R \right\rangle = \frac{{{{\left[ {\sum\limits_{i = 1}^N {} \varepsilon _{{{21}_i}}^{^2}} \right]}^{\frac{1}{2}}}}}{{{{\left[ {\sum\limits_{i = 1}^N {} \varepsilon _{{{32}_i}}^{^2}} \right]}^{\frac{1}{2}}}}}。$ | (25) |
其中:i=1, 2,…,N表示研究区域的N个点。由于范数总是大于0,无法识别出R < 0的情况,因此需要用该点附近的局部极值代替该点进行计算来辅助判断R的正负。
随着网格加密解的变化趋势不同,对应的截断误差的分析方法不同:
(1) 单调收敛误差和不确定度的分析方法
单调收敛可以用Richardson外推法进行误差和不确定度分析。
| $\delta _{RE}^* = {{\hat S}_1} - \hat S = \frac{{{{\hat S}_2} - {{\hat S}_1}}}{{{r^P} - 1}} = \frac{{{\varepsilon _{21}}}}{{{r^P} - 1}}。$ | (26) |
其中:P为指数,取决于所采用的离散格式。
上述截断误差分析方法是针对只存留截断误差首项时的方法,假设高阶项相对首项可忽略不计,对于较精细的网格且解处于渐近线范围内时,高阶项可以被忽略。然而在实际情况下,要达到渐近线范围内是不可能的,但因为进行包含2项及以上的截断误差的分析是很困难的,同时还需要在5套以上的网格上进行计算,所以不希望采用2项或以上的截断误差进行分析。解决的办法是考虑高阶项的影响,即对式(26) 进行修正,修正系数为:
| $C = \frac{{{r^P} - 1}}{{{r^{{P_{est}}}} - 1}}。$ | (27) |
其中:Pest为截断误差首项精度阶的估计值,可以取第一项的阶数。C < 1表明高阶项和为负值;C>1表明高阶项和为正值。这样,截断误差就可表示为:
| $ \delta _T^* = C\delta _{RE}^* = C\frac{{{\varepsilon _{21}}}}{{{r^P} - 1}}。$ | (28) |
采用解析基准解进行分析后表明不确定度UT可以取
| ${U_T} = \left| {C\delta _{RE}^*} \right| + \left| {\left( {1 - C} \right)\delta _{RE}^*} \right|。$ | (29) |
(2) 振荡收敛不确定度分析方法
振荡收敛只能估计不确定度而无法估计误差,不确定度的估计需要3套以上网格的解,具体公式为:
| ${U_T} = \left| {\frac{1}{{0.845}}({S_U} - {S_L})} \right|。$ | (30) |
其中:SU和SL分别为3套网格中解的最大值和最小值。式(30) 是这样得出的:假设模拟误差分布属于正态分布,这样扩展不确定度对应95%的置信度的包含因子就等于2,即
| ${U_T} = 2u。$ | (31) |
其中:95%为标准不确定度,当用单次的模拟值作为模拟值的估计值时,标准不确定度为实验标准差S。考虑到数据少于6个,用极差法求其标准差
| $S = \frac{{{S_U} - {S_L}}}{{1.69}}。$ | (32) |
这样,当解随网格加密振荡收敛时,置信度为95%的截断误差不确定度的计算式即为式(30)。
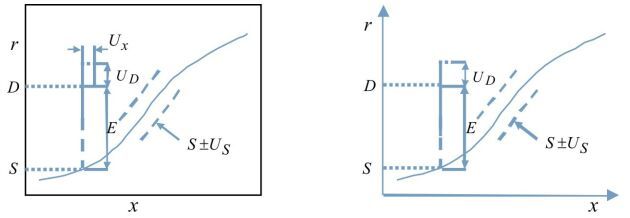
模型确认方法是综合考虑了模拟结果和实验数据中的误差及不确定度。用实验数据对模拟结果进行确认或比较误差可以通过图 7来解释。图中横坐标表示自变量x,纵坐标表示要考察的响应量(变量)r,某一自变量对应的模拟结果为S,对应的实验数据为D,S和D之间的差别用E表示,实验数据D存在不确定度UD,模拟结果S存在不确定度US。
|
图 7 比较误差定义 |
设实验数据D的误差为δD,根据式(1) 可以得到
| $D - {\delta _D} = S - {\delta _S}。$ | (33) |
D和S之间的差别E称为比较误差,可表示为:
| $\begin{array}{l} E = S - D = {\delta _S} - {\delta _D} = ({\delta _{SM}} + \delta _{SN}^* + {\varepsilon _{SN}}) - {\delta _D}\\ = ({\delta _{SMA}} + {\delta _{SPD}} + \delta _{SN}^* + {\varepsilon _{SN}}) - {\delta _D} \end{array}。$ | (34) |
其中:建模误差δSM被分为来自于模拟采用的参数误差δSPD和来自于模型假设的误差δSMA。
如果x,r和S没有共同的误差源,则比较误差的不确定度UE可以表示为:
| $U_E^2 = U_D^2 + U_S^2 = U_D^2 + U_{SMA}^2 + U_{SPD}^2 + U_{SN}^2。$ | (35) |
确认就是要比较|E|,UE和允许的最大不确定度Ureqd之间的关系,确认标准如下:
(1) 当|E|和UE都小于Ureqd时,模型通过确认。
(2) 在条件(1) 成立的情况下,如果|E| < UE,可以认为实验与模拟的偏差是由随机误差产生的,即认为模拟误差为0,这种情况下建模误差δSM与数值误差大小相等,符号相反。
(3) 在条件(1) 成立的情况下,如果UE < |E|,假定δD为0,则|E|可近似代表模拟误差,即建模误差和数值误差之和。
对多个模型或程序的检验除了进行单个模型或程序的检验外,还可以通过比较各个模型或程序的|E|+UE的大小,判断不同模型或程序的性能。
但实际上没有办法确定USMA,所以UE没法确定,因此引入不确定度UV来进行近似比较:
| $U_V^2 = U_E^2 - U_{SMA}^2 = U_D^2 + U_{SPD}^2 + U_{SN}^2$ | (36) |
对数据点(xi, ri),UD应该包括实验数据ri中的不确定度和n个自变量的测量不确定度附加给ri的不确定度,即
| $U_D^2 = {U_{{r_i}^2}} + \sum\limits_{j = 1}^n {} \left( {\frac{{\partial r}}{{\partial {r_j}}}} \right)_i^2({U_{{x_j}}})_i^2U。$ | (37) |
因使用已知参数带来的误差为:
| $U_{SPD}^2 = \sum\limits_{i = 1}^m {} {\left( {\frac{S}{{{D_i}}}} \right)^2}{({U_{{D_i}}})^2}。$ | (38) |
USN在验证的过程中已经得出,这样式(36) 右边的3项都可以计算得出,UV就可以求得。
需要说明的是解析基准解只能用于估计验证中的模拟误差,不能用于估计确认过程的建模误差。
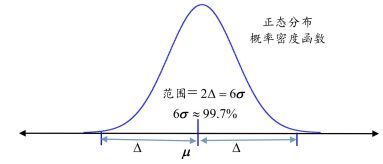
2.3 模型确认方法及可信度评估模型确认有两种方法。它们的主要区别在于计算SRQ与试验SQR的不确定性量化信息的来源。在CFD中模型不确定度量化主要是基于试验数据。当只有一种试验数据和仿真数据可用时,方法1是一种行之有效的确认方法。方法1需要领域内专家对试样和模型给出评估意见,领域内专家可能是,也可能不是实验人员或建模人员。基于他们过去在相关领域的经验,每个专家都要估计出一个对称的变化区间,所有实际值都要落在这个区间范围之内,区间的半带宽△如图 8所示。在缺乏数据时为方便和简化起见,认为△满足高斯(正态)分布。方法1中,测量或计算值认为是概率分布的均值(μ),半带宽△等于3倍标准差(3σ)。在图 8中整个△所覆盖的概率为99.7%, 标准差σ很容易由△计算获得。
|
图 8 评估概率密度分布函数、不确定因素 |
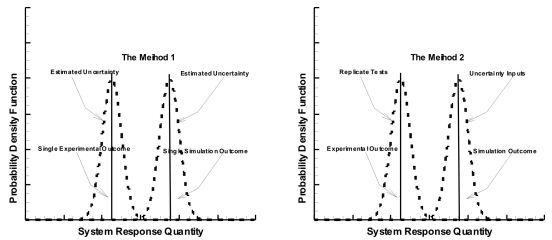
方法2与方法1类似,只是在对试验结果的不确定性量化分析时采用重复试验,而仿真结果的不确定性量化分析是通过对不同类型模型的重复试验不确定模型输入概率分析获得。因此,结果的概率密度函数(PDFs)可能不满足高斯分布,甚至不满足对称分布。这两种方法的假设理论如图 9所示。
|
图 9 两种确认方法图示说明 |
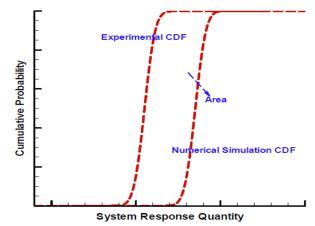
两种方法的确认指标都是基于测量SRQ值和计算SRQ的累积分布函数(CDFs,CDF是PDF的积分)之间的区域。这个指标有时被称为面积指标,如图 10所示。
|
图 10 面积指标示意图 |
面积度量MSRQ是试验CDF和模型CDF之间的面积区域,由试验结果的平均值进行归一化处理。因此,如果FSRQ(y)是模型预测SRQ和试验测量SQR的CDF值,那么
| ${M^{SRQ}} = \frac{1}{{\bar S\bar R{{\bar Q}^{\exp }}}}\smallint _{ - \infty }^{ + \infty }|{F_{SR{Q^{\bmod }}}}\left( y \right) - {F_{SR{Q^{\exp }}}}\left( y \right)|dy。$ | (39) |
其中:${\bar S\bar R{{\bar Q}^{\exp }}}$=实验输出结果的平均值。
这个度量值为非负数值,且只有当两种CDFs值完全相同时为0。为了帮助理解这个度量的含义,这里用一个两种CDFs值不相交的特殊例子来描述,式(39) 表示的是两种平均值之差的绝对值的积分,一般情况下,这种平均插值是SRQmod和SRQexp之间的差值的绝对值的均值下限。在确定的情况下,其中两个CDFs都是阶梯函数,该区域可简单表述为两个特定值之间差的绝对值。
两种确认方法,确认需求是:
| ${M^{SRQ}} \le 0.1。$ | (40) |
显然,一个特定的确认需求达到满意的结果是确认评估所期望。然而,V&V计划中应该包含验证需求不符合指标时的行动计划。这种应急计划可能包括改进模型、改进确认实验、更好地进行不确定性量化分析、放宽指标或它们之间的组合等,选择那种改进方法取决于主要应用情况、确认失败的结果以及确认可用的资源等。
3 结论与建议本文针对计算流体力学建模与模拟过程,将“物理建模、数值建模、软件研制、数值实验、结果分析”五位一体考虑,系统分析了各阶段误差与不确定性来源及可信度评估因素,给出了爆轰计算流体力学建模与模拟验证、确认和不确定度量化(V&V&UQ)的策略以及V&V&UQ过程中数值误差分析与不确定度量化方法。
验证与确认(V&V)技术已经成为欧美先进企业发展高可信度仿真软件的标准流程,并对众多工程仿真软件实施了V&V。在一些企业中,虚拟试验平均取代了70%以上的物理试验,甚至在某些行业做到了完全取代真实试验。但国内目前V&V&UQ方法及应用仍处于发展阶段,许多理论和方法问题有待解决。
(1) 复杂外形网格收敛指标验证技术。验证与确认中要求对数值计算误差分析,生成3套及3套以上的相似网格是非常重要的。这点对现在越来越复杂几何外形,生成拟相似网格需要付出很大的时间和精力。即对复杂外形这是一个很具挑战性的难题。
(2) 基于模型分层确认方法。复杂工程流体力学领域涉及多物理过程耦合,要开展模型确认,必须将复杂过程进行层级分解,构建模型分层确认树型图,才能有效开展确认试验,达到评估数值模拟结果可信度的目的。为此未来必须重视模型层级确认方法的发展。
(3) 多参数、多因素、多层级等多物理过程不确定性适用的数学描述及量化的数学方法。参数作为随机变量处理具有一定的合理性,但不能适合参数变化的所有情况,不同情况下参数可能取值的变化,很难满足随机分布的假定,这就要求对参数不确定性发展提供更为适用的数学描述及量化方法。
| [1] | Oberkampf W. L, Roy C. J. Verification and validation in scientific computing[M]. New York: Cambridge University Press, 2010. |
| [2] | 王瑞利, 粱霄, 林文洲, 等. 基于微分方程工程仿真软件的验证与确认[C]. 桂林: 第11届中国CAE工程分析技术年会论文集, 2015: 95-107. |
| [3] | 王瑞利, 温万治. 复杂工程建模与模拟的验证与确认[J]. 计算机辅助工程, 2014, 23(4): 61–68. |
| [4] | 邓小刚, 宗文刚, 张来平, 等. 计算流体力学中的验证与确认[J]. 力学进展, 2007, 37(2): 279–288. DOI:10.6052/1000-0992-2007-2-J2005-149 |
| [5] | WANG Rui-li, LIANG Xiao, LIN Wen-zhou, et al. Verification and validation of the detonation computational fluid dynamics model[J]. Defect and Diffusion Forum, 2016, 366: 40–46. DOI:10.4028/www.scientific.net/DDF.366 |
| [6] | 王瑞利, 江松. 多物理耦合非线性偏微分方程与数值解不确定度量化数学方法[J]. 中国科学:数学, 2015, 45(6): 723–738. |
| [7] | WANG Rui-li, LIANG Xiao, LIN Zhong. Altering connectivity with large deformation mesh for Lagrangian method and its application in multiple material simulation[J]. Annals of applied mathematics, 2016(3): 296–310. |
| [8] | 王瑞利, 刘全, 温万治. 非嵌入式多项式混沌法在爆轰产物JWL参数评估中的应用[J]. 爆炸与冲击, 2015, 35(1): 9–15. DOI:10.11883/1001-1455(2015)01-0009-07 |
| [9] | 梁霄, 王瑞利. 混合不确定度量化方法及其在计算流体动力学迎风格式中的应用[J]. 爆炸与冲击, 2016, 36(4): 509–515. DOI:10.11883/1001-1455(2016)04-0509-07 |
| [10] | Helton J. C.Conceptual and Computational Basis for the Quantification of Margins and Uncertainty[R].SAND2009-3055, 2009. |
| [11] | Karniadakis G. E, Glimm J. Preface:Uncertainty Quantification in Simulation Science[J]. Academic Press Professional, Inc, 2006(1): 1–4. |
| [12] | 王瑞利, 梁霄. 爆轰数值模拟中物理模型分层确认实验研究[J]. 中国测试, 2016, 42(10): 13–20. DOI:10.11857/j.issn.1674-5124.2016.10.003 |
| [13] | 梁珍, 沈恒根, 张吉礼, 等. CFD模拟中的误差分析——验证与检验[J]. 暖通空调, 2008(增刊): 277–282. |
| [14] | 梁珍, 载人航天器通风气流模拟及轻量化分析[D]. 哈尔滨: 哈尔滨工业大学博士学位论文, 2007. |
 2017, Vol. 32
2017, Vol. 32