太阳能具有无污染、永不枯竭和采集便利等优点[1],建立准确的光伏阵列模型是光伏发电系统研究的基础,对MPP跟踪算法研究、光伏阵列优化布局设计和变换器控制设计等问题都有重要的实际意义[2-3]。光伏阵列具有强非线性、多输入的特点,其输出受温度和辐照强度等环境因素影响变化很大,国内外学者提出了多种光伏阵列的建模方法:文献[4]提出了一种考虑温度、辐照强度的光伏模型,并且讨论了负载变化的影响,但没有分析阴影对光伏特性的影响;文献[5-6]通过引入系数典型值的方法考虑了环境参数的影响,在MATLAB环境下建立了满足工程精度且便于运算的光伏组件通用模型,但未能实现阴影条件下的仿真;文献[7-8]通过实验获得了光伏模块I-V特性,虽然研究了局部阴影条件下的效果,但仅限于模块级研究,并没有拓展到光伏阵列上。为了避开复杂阴影条件下的建模困难,另一些方法[9-10]通过引入智能算法来获取典型的5个参数,但是需要大量的实验数据作为支撑,因此限制了其应用。
然而,光伏阵列在实际运行过程中光照程度经常受到周围环境影响,如高层建筑物、树荫、塔杆等物体的遮挡,使光伏阵列出现局部阴影问题。在局部阴影条件下,光伏发电系统的输出功率将会大大降低,并呈现多个局部最大功率点 (Maximum Power Point,MPP),使一些常用的MPP跟踪算法陷入局部极值而失效,而某些太阳能板可能会工作在第二象限,成为负载吸收功率形成热斑损坏组件。光伏阵列输出特性变化与阴影的面积大小、形状及辐照强度最弱的电池板有着密切关系。光伏阵列在局部阴影条件下的输出特性与均匀光照条件下具有明显区别,为了在局部阴影条件下提高光伏阵列光伏发电系统性能,需要在原有光伏阵列中加装旁路二极管。[11-12]这样,就改变了电流的路径,原有模型不再适用,需要重新建立局部阴影条件下的光伏阵列模型。
1 光伏阵列的建模 1.1 双二极管光伏阵列模型光伏电池的等效电路模型主要有理想等效电路模型、单二极管等效电路模型和双二极管等效电路模型等[13-14]。双二极管等效电路模型考虑了反向雪崩击穿效应,具有更高的工程精度。
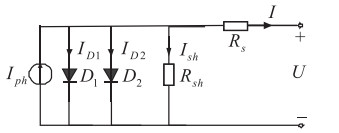
图 1为光伏电池双二极管等效电路模型,图中Iph为光生电流源,ID1表示流过二极管D1的电流,ID2表示流过二极管D2的电流,Rs为串联电阻,Rsh为损耗的并联电阻。
|
图 1 光伏电池双二极管等效电路 |
对此模型运用KCL定律可得光伏电池输出电流为:
| $ I = {I_{ph}}-{I_{{D_1}}}-{I_{{D_2}}}-{I_{sh}}。 $ | (1) |
其中:
| $ {I_{ph}} = {I_{sc}}\left( {\frac{S}{{1000}} + {K_0}(T-{T_{ref}})} \right), $ | (2) |
| $ {K_0} = \frac{{{I_{SC({T_2})}}-{I_{SC({T_1})}}}}{{{T_2}-{T_1}}}, $ | (3) |
| $ {I_{{D_1}}} = {I_{{s_1}}}({e^{\frac{{q\left( {U + I{R_s}} \right)}}{{{a_1}kT}}}}^{}-1), {\rm{ }} $ | (4) |
| $ {I_{{D_2}}} = {I_{{s_2}}}({e^{\frac{{q\left( {U + I{R_s}} \right)}}{{{a_2}kT}}}}-1), $ | (5) |
| $ {\rm{ }}{I_{si}} = {I_{do}}{(\frac{T}{{{T_{ref}}}})^3}({\rm{exp}}[\frac{{q{E_g}}}{{{a_i}k}}(\frac{1}{{{T_{ref}}}}-\frac{1}{T})]), $ | (6) |
| $ {I_{sh}} = \frac{{U + I{R_s}}}{{{R_{sh}}}}。 $ | (7) |
其中:I为光伏电池输出电流,单位为A;U为光伏电池输出电压,单位为V;S为光照强度,单位为W/m2;Isc为短路电流,单位为A;q为电子电量,单位为1.602×10-19C;T和Tref分别为绝对温度和电池表面温度,单位为K;k为玻尔兹曼常数,单位为1.38×10-23J/K;Is1和α1分别为二极管D1反向饱和电流和品质因子;Is2和α2分别为二极管D2反向饱和电流和品质因子;Eg为能带系能量常数。
光伏电池一般通过串、并联构成光伏阵列。(8) 式为由双二极管光伏电池组成的光伏阵列的数学模型:
| $ I = {N_P}{I_{ph}}-{N_P}{I_{{s_1}}}({e^{\frac{{q\left( {U/{N_s} + I{R_s}/{N_P}} \right)}}{{^{{a_1}kT}}}}}-1)-{N_P}{I_{{s_2}}}({e^{\frac{{q\left( {U/{N_s} + I{R_s}/{N_P}} \right)}}{{^{{a_2}kT}}}}} - 1) - {N_P}\frac{{U/{N_s} + I{R_s}/{N_P}}}{{{R_{sh}}}}。 $ | (8) |
其中:NS和NP分别为串联和并联的光伏电池数。
1.2 光伏阵列输出特性分析选择典型的Solarex MSX60型光伏组件用于建模,该模块由36个多晶电池组合构成,生产厂商提供给用户的试验参数 (在标准测试环境下测量的数据,温度t=25 ℃,辐照强度S=1 000 W/m2) 如表 1所示。
| 表 1 Solar MSX60型光伏组件参数 (t=25 ℃,S=1 000 W/m2) |
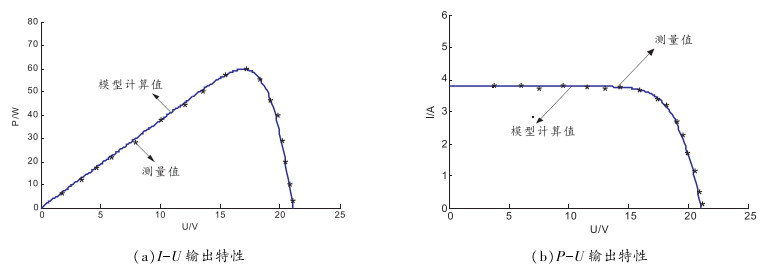
根据上述数学模型,得到光伏阵列在标准测试环境下的I-U输出特性和P-U输出特性,与实验测量曲线进行比较,如图 2所示。
|
图 2 模型计算值与实际测量值比较 |
从图 2可以看出,所提模型理论计算值与实际测量值吻合较好。误差存在的原因是在仿真计算中为了问题分析简单,认为串、并联在一起的光伏电池具有相同的特征参数,忽略了二极管损耗和光伏电池之间的连接电阻,但是误差在工程精度许可的范围以内。
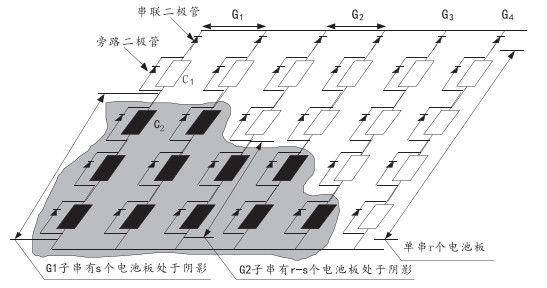
2 局部阴影条件下光伏阵列的建模 2.1 旁路二极管对光伏阵列的影响分析图 3为局部阴影条件下的光伏阵列示意图。当光伏阵列处于局部阴影的条件下,光伏组件中电池元由于辐照强度不同其输出特性将不再一致,可能出现局部过热而损坏模组的现象。在图 3中的G1双串阵列中,电池C1处于正常光照条件下,而电池C2处于阴影中,则对应输出电流IC2 < IC1,而流过C1和C2的电流均为IC2。这样,电池C2就成为C1的负载,工作在第二象限且吸收功率,时间过长就会造成C2过热损坏。因此,模型 (8) 式在局部阴影条件下的光伏阵列不再适用,需要对电路进行改进并重新建立模型。
|
图 3 局部阴影条件下光伏阵列示意图 |
为了避免上述现象,一般需要在光伏阵列中的电池板并联二极管。在图 3中的每个电池元都并联了旁路二极管,当电池正常工作时二极管截止,而负载工况时二极管导通,这样电流不再通过电池,从而起到保护电池的作用。在每双串列中串联了二极管,也起到了保护作用。由于二极管改变了电流的路径,因此会对输出造成影响。
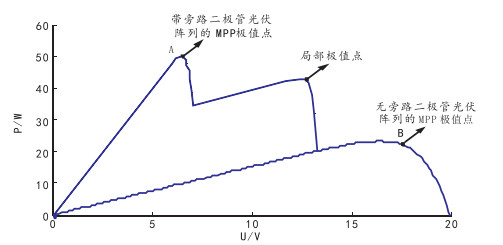
图 4为局部阴影条件下旁路二极管对光伏阵列P-U曲线影响,带旁路二极管曲线A的MPP比无旁路二极管曲线B的MPP高41.2%。可见,旁路二极管能有效提高输出功率,而且能对组件形成保护。需要注意的是,光伏阵列带旁路二极管后输出功率会出现多个极大值,而且大部分的MPP跟踪算法对局部和全局最大值之间可能无法区分。另外,旁路二极管数量越多,则电路复杂性越高,成本也越大[15-16];当旁路二极管达到一定数量时对输出功率的提高就会变得十分有限。因此实际安装旁路二极管的数量要结合复杂度与成本而综合考虑。
|
图 4 局部阴影条件下旁路二极管对光伏阵列P-U曲线影响 |
不考虑温度的变化,引入光照因子λ来描述阴影的透光情况:
| $ \lambda = \frac{{{S_b}}}{{{S_0}}}。 $ | (9) |
其中:Sb为遮光后的辐照强度,单位为W/m2;S0为标准辐照强度,一般取为1 000 W/m2。
为了便于精确分析阴影的影响,将图 3中具有相同光照条件和温度的电池板划分成一组。选取具有2个子串串联电池板的子阵列G作为基本单元,各子串包含了r个电池元。为了讨论的一般性,设在G1子串中有s个电池元处于阴影中,而与之相邻的G2子串中有r-s个电池元处于阴影中,则划分的光伏子阵的关系如下:
| $ \left\{ \begin{array}{l} {I_{ph}}_{_1} = s{I_{ph}}({G_1}), \\ {I_{p{h_2}}} = \left( {r-s} \right){I_{ph}}({G_2}). \end{array} \right. $ | (10) |
因此,光伏阵列的输出电流表示为:
| $ I = \left\{ \begin{array}{l} {I_{ph}}({G_1}) - {I_{s1}}({e^{\frac{{q\left( {U + I{R_s}} \right)}}{{{a_2}kT}}}} - 1) - {I_{s2}}({e^{\frac{{q\left( {U + I{R_s}} \right)}}{{{a_2}kT}}}} - 1) - \frac{{({U_1} + I{R_s}{N_s})}}{{{N_s}{R_{sh}}}},I > {I_{p{h_1}}},\\ {I_{ph}}({G_2}) - {I_{s1}}({e^{\frac{{q\left( {U + I{R_s}} \right)}}{{{a_2}kT}}}} - 1) - {I_{s2}}({e^{\frac{{q\left( {U + I{R_s}} \right)}}{{{a_2}kT}}}} - 1) - \frac{{({U_1} + I{R_s}{N_s})}}{{{N_s}{R_{sh}}}},I < {I_{p{h_2}}}。 \end{array} \right. $ | (11) |
图 3中任意阴影条件下的光伏阵列数学模型为:
| $ \left\{ \begin{array}{l} I = {\rm{min}}\left( {{I_i}} \right), \\ U = \Sigma {U_i}. \end{array} \right. $ | (12) |
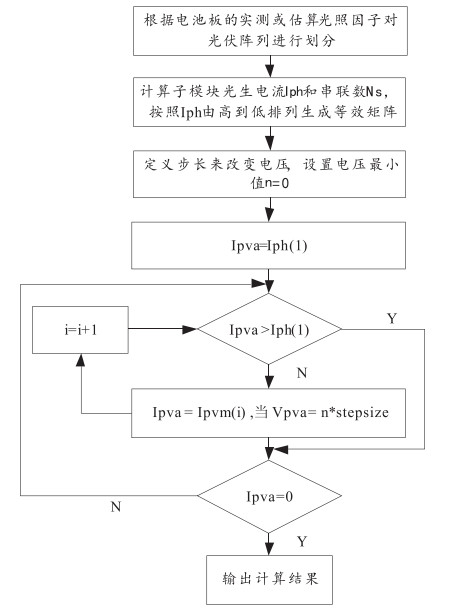
光伏阵列的组成包含多个子阵列模块,阵列的输出特性由于阴影的存在而变得更加复杂,对其进行精确计算需要合理分析方法。局部阴影条件下光伏阵列输出计算的流程如图 5。其中Ipvm(i) 为计算电流最小值。
|
图 5 局部阴影条件下光伏阵列输出特性计算流程图 |
在阴影条件下进行模型分析首先要根据实际阴影情况对阵列进行划分,再按照光生电流和电池串联数量得到的等效矩阵,结合光照因子分区段计算结果。
3 局部阴影条件下光伏阵列输出特性分析阴影的分布和大小对光伏阵列的输出特性会产生影响,按照3种不同的遮光模式对上述模型进行仿真:
(1) 整个阵列处于均匀光照条件,光照因子λ=1;
(2) 在阵列中有7个电池板处于局部阴影,光照因子λ=0.6;
(3) 在阵列中有9个电池板处于局部阴影,其中5个电池板光照因子λ=0.4,另外4个电池板光照因子λ=0.2。
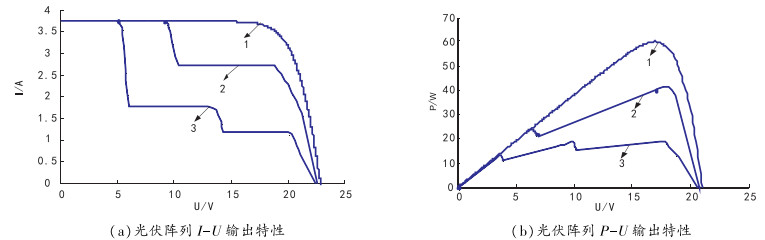
图 6为对应3种模式的局部阴影条件下光伏阵列输出特性。图 6(a)为局部阴影条件下光伏阵列I-U输出特性,可以看出,阵列的I-U曲线随着阴影存在多个阶梯,阶梯的数量和阴影的等级数量相同,输出电流随着辐照因子的增大而减小。图 6(b) 为局部阴影条件下光伏阵列P-U输出特性,图中曲线1只有1个极值点,曲线2和3分别出现了2个和3个极值点,而每条曲线只有1个最大值。
|
图 6 局部阴影条件下光伏阵列输出特性 |
根据仿真结果,可以得出如下关于阴影与光伏阵列输出的结论:
(1) 局部阴影的存在使I-U和P-U曲线呈现出阶梯状,阶梯个数与阴影辐照强度区域数相同;
(2) 阴影对输出功率的影响十分明显,输出功率的大小与阴影分布形式和阵列排列有密切关系;
(3) 局部阴影条件下,会出现多个局部极值点,但只要一个全局最大值,这将导致某些MPP跟踪算法失效,为了获得最大功率在算法设计时需要避免陷入局部极值。
4 结语针对光伏阵列的局部阴影问题,以双二极管光伏电池为基础建立光伏阵列工程数学模型,分析了局部阴影条件下光伏电池元的工作差异,建立了带旁路二极管的光伏阵列数学模型。对所提模型在不同环境温度和辐照强度条件下对组件进行仿真测试和分析,得到了阴影对光伏阵列的输出影响关系。结果表明,所提模型能准确反映不同条件下光伏组件的输出特性,为大型光伏发电系统优化设计提供了支持。
| [1] | 赵争鸣. 太阳能光伏发电及其应用[M]. 北京: 科学出版社, 2005. |
| [2] | 张鹏. 光伏并网系统控制策略研究与仿真[J]. 电器与能效管理技术, 2015(4): 56–59. |
| [3] | Walker GR. Evaluating MPPT converter topologies using a MATLAB PV Model[J]. Journal of Electrical & Electronics Engineering, 2001, 21(1): 49–55. |
| [4] | 苏建徽, 余世杰, 赵为, 等. 硅太阳电池工程用数学模型[J]. 太阳能学报, 2005, 20(5): 409–412. |
| [5] | 彭乐乐, 孙以泽, 孟婥, 等. 光伏太阳能电池组件Matlab通用仿真模块[J]. 东华大学学报 (自然科学版), 2009, 37(1): 90–94. |
| [6] | 茆美琴, 余世杰, 苏建徽. 带有MPPT功能的光伏组件Matlab通用仿真模型[J]. 系统仿真学报, 2005, 17(5): 1248–1251. |
| [7] | Patel H, Agarwal V. MATLAB-based Modeling to Study the Effects of Partial Shading on PV Array Characteristics[J]. IEEE Transaction on Energy Conversion, 2008, 23(1): 302–310. DOI:10.1109/TEC.2007.914308 |
| [8] | Villalva M.G, Gazoli J.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays[J]. IEEE Trans.Power Electron, 2009, 24(5): 118–1208. |
| [9] | 胡海燕, 胡克满, 王民权. 基于BP神经网络双硅太阳电池模型参数的解析研究[J]. 计算机应用与软件, 2014, 31(3): 55–58. |
| [10] | 郭亮, 陈维荣, 贾俊波, 等. 基于粒子群算法的BP神经网络光伏电池建模[J]. 电工电能新技术, 2011, 30(2): 84–88. |
| [11] | 田琦, 赵争鸣, 韩晓艳. 光伏电池模型的参数灵敏度分析和参数提取方法[J]. 电力自动化设备, 2013, 33(5): 119–124. |
| [12] | 胡克满, 胡海燕, 柳桂国. 太阳电池I-V曲线拟合的优化算法[J]. 计算机应用, 2013, 33(5): 1481–1484. |
| [13] | 张超, 何湘宁. 短路电流结合扰动观察法在光伏发电最大功率点跟踪控制中的应用[J]. 中国电机工程学报, 2006, 26(20): 98–102. DOI:10.3321/j.issn:0258-8013.2006.20.017 |
| [14] | 王章权, 张超, 何湘宁. 基于Pspice模拟行为模型的光伏阵列建模[J]. 计算机仿真, 2007, 24(8): 225–240. |
| [15] | GB/T 6495. 4-1996, 晶体硅光伏器件的I-V实测特性的温度和辐照度修正方法[S]. |
| [16] | 刘邦银, 段善旭, 康勇. 局部阴影条件下光伏模组特性的建模与分析[J]. 太阳能学报, 2008, 29(2): 188–192. |
 2017, Vol. 32
2017, Vol. 32