武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 218-222

文章信息

刘凯, 李文佩, 程潜善, 方华亮
LIU Kai, LI Wenpei, CHEN Qianshan, FANG Hualiang
基于启发式规则和人工免疫的智能配电网自愈
Self-healing of smart distribution network based on heuristic rules and artificial immune
武汉大学学报(工学版), 2016, 49(2): 218-222
Engineering Journal of Wuhan University, 2016, 49(2): 218-222
http://dx.doi.org/10.14188/j.1671-8844.2016-02-010

文章历史

收稿日期: 2015-05-11
 Abstract              PDF               Figures               Tables
引用本文 0
刘凯, 李文佩, 程潜善, 方华亮. 基于启发式规则和人工免疫的智能配电网自愈[J]. 武汉大学学报(工学版), 2016, 49(2): 218-222.
LIU Kai, LI Wenpei, CHEN Qianshan, FANG Hualiang. Self-healing of smart distribution network based on heuristic rules and artificial immune[J]. Engineering Journal of Wuhan University, 2016, 49(2): 218-222.
基于启发式规则和人工免疫的智能配电网自愈
刘凯, 李文佩, 程潜善, 方华亮     
武汉大学电气工程学院，湖北 武汉 430072
收稿日期: 2015-05-11
作者简介: 刘凯（1990-），男，硕士研究生，研究方向为电力系统运行与控制，E-mail：liukai9036@163.com.
通讯作者: 方华亮（1978-），男，工学博士，副教授，从事电力系统分析方面的研究工作，E-mail：hlfang@whu.edu.cn
基金项目: 国家自然科学基金项目（编号：51107090）.
摘要: 为了快速得到智能配电网故障后的最优自愈方案，提出了一种基于启发式规则和人工免疫的配电网自愈方法.首先，分析了免疫抗体选择过程和电网自愈方案选择过程的相似性，并提出电网自愈的数学模型.然后，根据启发式规则生成自愈方案候选集.最后，利用人工免疫方程从负荷停电损失、网络损失和开关操作次数3个方面对所有自愈方案进行综合评价，确定最优的自愈方案.以五馈线配电网络为例，对其发生故障后自愈方案的选择进行仿真分析.仿真结果验证了该方法的可行性和有效性.
关键词： 配电网自愈     自愈模型     启发式规则     人工免疫    
Self-healing of smart distribution network based on heuristic rules and artificial immune
LIU Kai, LI Wenpei, CHEN Qianshan, FANG Hualiang     
School of Electrical Engineering, Wuhan University, Wuhan 430072, China
Abstract: In order to obtain optimal self-healing program after the failure of the smart distribution network quickly, the heuristic rules and artificial immune method based on self-healing distribution network are proposed. Firstly, the similarity of antibody selection process and self-healing grid program selection process are compared and the mathematical model of self-healing grid is proposed. Then, the self-healing program generates a candidate set based on heuristic rules. Finally, by using artificial immune from load power loss equation, network losses and the number of switching operations of all three aspects of self-healing program, a comprehensive assessment is given to determine the optimal healing program. In this paper, the five-feeder distribution network is shown for example and simulations of the choices after a failure of self-healing solutions are analyzed. Simulation results verify the feasibility and effectiveness of this method.
Key words: self-healing of distribution network；self-healing model；heuristic rules；artificial immune    

智能电网主要由智能输电网和智能配电网组成.目前，我国在建设坚强、可靠的智能输电网方面已经取得了一定的成就[1-3]，但配电网的供电可靠性却比较低.智能配电网直接面向用户，其供电可靠性和供电质量十分重要.智能配电网的自愈控制，能够使配电网在故障情况下进行网络重构和供电恢复，提高配电网的供电可靠性.

大量文献对智能配电网的自愈模型和自愈算法进行了研究和探讨.文献[4]提出了智能配电网的自愈控制目标、技术方案与实施条件.配电网的自愈算法主要可分为3类：数学规划法[5]、人工智能算法[6-8]和启发式搜索算法[9].然而，对于规模较大的配电网而言，数学规划法和人工智能算法均存在计算时间长、实时性不强的问题[10].启发式搜索算法虽然能够快速生成可行的自愈方案，却无法给出最优自愈方案.

本文提出基于启发式规则和人工免疫的配电网自愈策略.在电网发生故障后，由启发式规则和候选方案集生成规则形成可行的自愈方案集.利用人工免疫动力学模型从负荷损失、网络损耗和开关动作次数3个方面对可行的自愈方案进行综合评价，快速获取智能配电网的最优自愈方案.

1 人工免疫与电网自愈

配电网有少量的联络开关和大量的分段开关.电网发生故障后，可以依据启发式规则生成自愈方案改变这些开关的状态，来恢复非故障失电负荷的供电,实现电网自愈.然而，启发式规则通常生成的是多个可行的自愈方案.不同的自愈方案对电网的自愈恢复程度是不同的，因此需要针对不同故障确定最优自愈方案.

免疫系统的主要功能是识别并排除从外界环境中入侵的抗原，维持人体内部环境的稳定.人工免疫系统是基于免疫系统机制和免疫学理论建立起来的各种人工系统的总称，具有学习、记忆和自我调整的能力，已广泛应用于模式识别、联想记忆、故障诊断和机器人控制等领域[11].免疫系统的作用机理可以用抗体与抗原之间、抗体与抗体之间相互作用来描述,文献[12]提出的人工免疫动力学模型为

$\begin{align} & \frac{d{{X}_{i}}}{dt}={{k}_{1}}\sum\limits_{j=1}^{M}{{{a}_{ij}}{{x}_{i}}{{y}_{j}}}-{{k}_{2}}\sum\limits_{k=1,k\ne i}^{N}{{{a}_{ik}}{{x}_{i}}{{x}_{k}}} \\ & +{{k}_{3}}\sum\limits_{l=1,l\ne i}^{N}{{{a}_{li}}{{x}_{l}}{{x}_{i}}}-{{k}_{d}}{{x}_{i}} \\ & {{x}_{i}}=\frac{1}{1+\exp (0.5-{{X}_{i}})} \\ \end{align}$    (1)

式中：N为抗体总数；M为入侵抗原的总数；yj为入侵抗原j的浓度；Xi为抗体i的受激励程度；xi为抗体i的浓度；αij为抗体i对抗原j的亲和力；αik为抗体k对抗体i的抑制作用；αli为抗体l对抗体i的激励作用；kd反映了抗体的自然死亡率.

利用免疫理论可以确定电网自愈的最优方案，将电网故障造成的失电负荷对应抗原，电网自愈方案对应抗体.自愈方案恢复失电负荷程度对应抗体对抗原的亲和力，若方案恢复失电负荷越多，则其受到的激励也就越大.不同自愈方案之间的相互激励或抑制由不同方案之间网络损耗的差值来确定.自愈方案的开关动作次数对应抗体自身的死亡率，若方案的开关动作次数较多，则其受到的激励也会减小.针对一个特定的故障抗原，利用免疫动力学模型可以确定一个浓度和所受激励最大的抗体，那么这个抗体就是当前故障环境下的最优自愈方案.

2 电网自愈数学模型 2.1 目标函数

电网自愈的优化目标主要包括以下3个方面.

1) 尽量减少负荷停电造成的损失

配电网中的负荷分为需要持续不断供电的重要负荷和必要时可以切除的普通负荷[13].电网自愈的首要任务是在保证重要负荷供电的情况下，尽可能多地恢复普通失电负荷的供电.停电引起的负荷损失函数可表示为

${{f}_{\Delta L}}={{\lambda }_{1}}\sum\limits_{i\in A}{{{x}_{i}}{{p}_{i}}}+{{\lambda }_{2}}\sum\limits_{j\in B}{{{y}_{j}}\Delta {{p}_{j}}}$    (2)

式中：A和B分别是配电网中重要负荷和普通负荷集合;pi是重要负荷i的功率;Δpj是普通负荷j的功率;xi和yj只能取0或1，当xi=0时，重要负荷i恢复供电,当xi=1时，重要负荷i失电;λ1和λ2分别表示单位重要负荷和单位普通负荷失电所造成的损失.

2) 网络损耗最低

配电网的网络损耗函数可表示为

${{f}_{\Delta p}}=\sum\limits_{i=1}^{N}{{{R}_{i}}(P_{i}^{2}+Q_{i}^{2})/|U|_{i}^{2}}$    (3)

式中：Ri是支路i的阻抗；Pi、Qi和Ui分别是支路i的有功功率、无功功率和电压；N是系统支路数.

3) 开关动作次数最少

在尽量减少停电损失的前提下，还要减少电网自愈过程中开关的动作次数.

${{f}_{\Delta N}}=\sum\limits_{i=1}^{{{N}_{s}}}{{{z}_{i}}}$    (4)

式中：Ns是系统中所有联络开关和分段开关数目；开关i的状态变化由zi来表示，当zi=1时，表示开关状态发生变化，当zi=0时，表示开关状态未发生变化.

综上所述，智能配电网多目标优化自愈的目标函数可以表示为

$F=\min ({{k}_{1}}{{f}_{\Delta L}}+{{k}_{2}}{{f}_{\Delta p}}+{{k}_{3}}{{f}_{\Delta N}})$    (5)

其中：k1、k2和k3分别是负荷损失函数fΔL、网络损耗函数fΔp和开关动作次数fΔN的权重系数，且k1远大于k2和k3.

2.2 约束条件

在电网自愈过程中，约束条件包括潮流方程约束、支路容量约束、节点电压约束和网络拓扑约束.

1) 潮流方程约束：

$\left\{ \begin{align} & {{P}_{i}}=\sum\limits_{j\to i}^{n}{{{U}_{i}}{{U}_{j}}({{G}_{ij}}\cos {{\theta }_{ij}}+{{B}_{ij}}\sin {{\theta }_{ij}})} \\ & {{Q}_{i}}=\sum\limits_{j\to i}^{n}{{{U}_{i}}{{U}_{j}}({{G}_{ij}}\cos {{\theta }_{ij}}-B\sin {{\theta }_{ij}})} \\ \end{align} \right.$    (6)

式中：n为系统节点数；Gij、Bij和θij分别是节点i与节点j之间的导纳和相角差；j→i表示节点j与节点i相连.

2) 支路容量约束：

${{P}_{k}}\le {{P}_{k\max }}$    (7)

式中：Pk是支路k中的有功功率；Pkmax是支路k中有功功率上限.

3) 节点电压约束：

${{V}_{i\min }}\le {{V}_{i}}\le {{V}_{i\max }}$    (8)

式中：Vimin和Vimax分别是节点i的电压下限和上限.

网络拓扑约束是指配电网在自愈过程中必须保持辐射状结构，不得出现环网.

3 配电网自愈策略

电网发生并切除故障后，为了满足自愈要求，需要对电网进行自愈操作.文献[14]给出了电网自愈的启发式规则和自愈方案候选集的生成方法，具体步骤如下:

1) 进行自馈线恢复.若无法恢复，转到步骤(2)；若可以恢复，转到步骤(5).

2) 计算失电总负荷和各馈线的负荷裕量，搜索相应联络开关和分段开关，进行整区或分区恢复.若无法恢复，转步骤(3)；若可以恢复，转步骤(5).

3) 将相邻馈线自身所带负荷向次相邻馈线进行转移，增大联络开关的容量，并转到步骤(2)进行整区或分区恢复.若无法进行负荷转移，转步骤(4).

4) 按事先确定好的优先级，切除部分负荷，转步骤(2)直到生成一个可行的自愈方案.

设可行的自愈方案包含p条相邻馈线和q条次相邻馈线，根据如下规则生成自愈方案候选集:

① 当p=1，q=0时，自愈方案候选集由两组方案组成：p条相邻馈线；p+1条相邻馈线.

② 当p>1,q=0时，自愈方案候选集由四组方案组成：p条相邻馈线；p+1条相邻馈线；p-1条相邻馈线和1条次相邻馈线；p条相邻馈线和1条次相邻馈线.

③ 当p=1，q>0时，自愈方案候选集为p+1条相邻馈线和q条次相邻馈线.

④ 当p>1，q>0时，自愈方案候选集为p条相邻馈线和q条次相邻馈线.

3.1 基于人工免疫的最优自愈方案评价

利用启发式规则和候选集生成规则可以快速确定电网自愈方案候选集，本文通过人工免疫动力学方程综合评价各自愈方案，确定最优自愈方案.将电网故障带来的非故障失电负荷看作抗原，将该故障对应的自愈方案看作抗体，根据人工免疫动力学方程可知抗原与抗体之间、抗体与抗体之间的相互作用关系如下：

$\left\{ \begin{align} & {{Y}_{i}}={{Y}_{i0}}+({{k}_{1}}{{m}_{i}}X+{{k}_{2}}\sum\limits_{j=1,j\ne i}^{N}{{{n}_{ij}}{{y}_{j}}}-{{k}_{i}}){{y}_{i}} \\ & {{y}_{i}}=\frac{1}{1+\exp (0.5-{{Y}_{i}})} \\ \end{align} \right.$    (9)
${{m}_{i}}=S(i)$    (10)
${{n}_{ij}}=\Delta p(j)-\Delta p(i)$    (11)

其中：yi是自愈方案i的浓度；Yi0是自愈方案i的初始受激励程度；Yi是自愈方案i受激励程度；N是抗原X对应的自愈方案候选集中自愈方案的数量；S(i)是方案i恢复的失电负荷；Δp(i)是方案i对应的网损；k1和k2是系数；ki是方案i对应的开关操作次数.

由式(9)~(11)可知，若方案i恢复失电负荷越多，同时其带来的网损和开关动作次数越少，该方案受到抗原和其他抗体的激励会越多、对应的浓度Yi也就越大，其被选中作为最优方案的概率也就越大.

3.2 配电网自愈算法流程

根据文献[14]中的启发式规则和3.1节中自愈方案评价方法，本文的配电网自愈算法流程如图 1所示.

图 1 算法流程 Figure 1 Flowchart of algorithm
图选项
4 算例分析

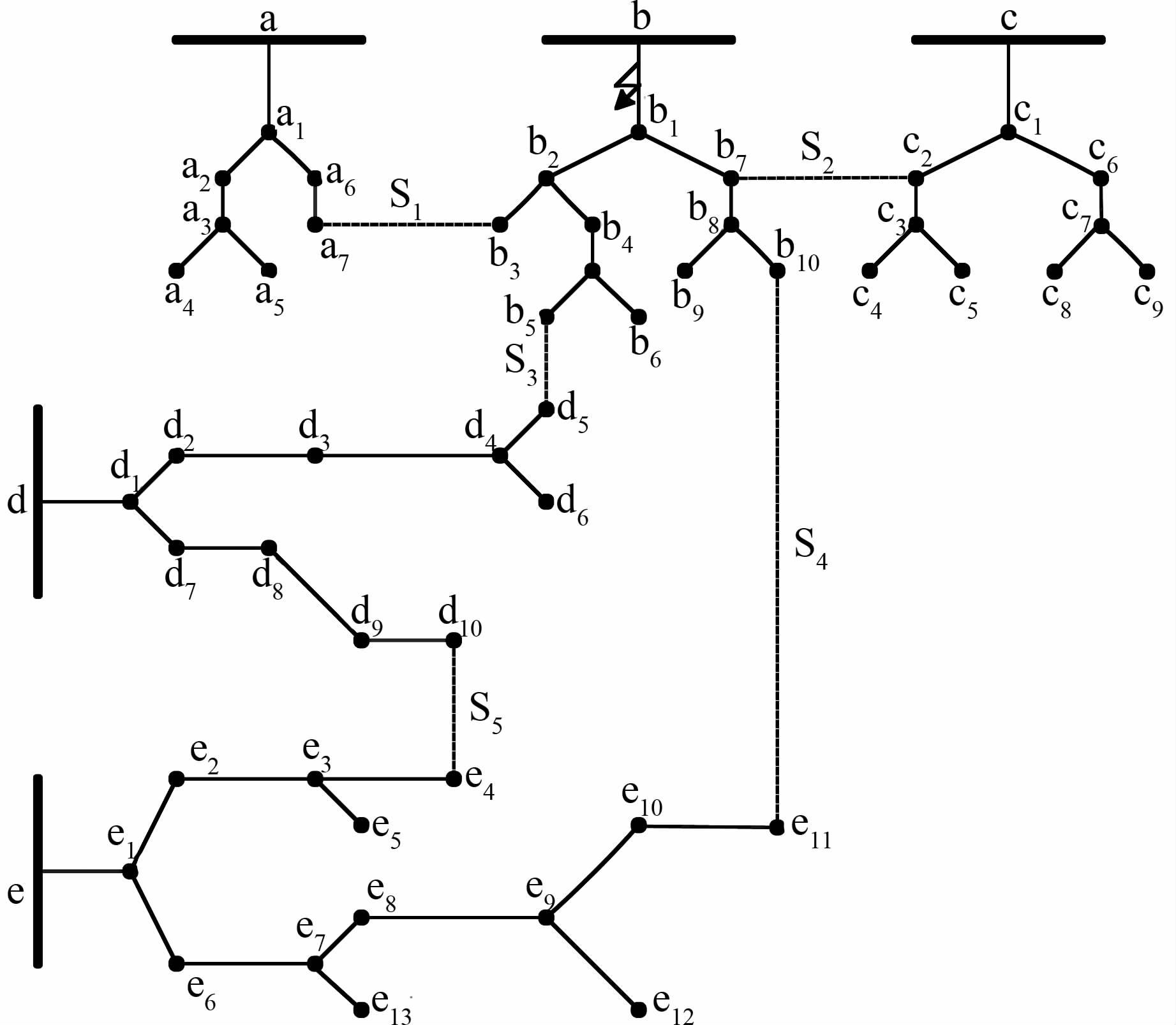
以如图 2所示的五馈线配电网络为例，其中实线代表分段开关，虚线代表联络开关，网络参数见文献[15].假设b与b1之间发生永久性故障，经故障隔离后b2的下游为非故障停电区域.

图 2 配电网算例 Figure 2 Example of distribution network
图选项

与停电区域直接相连的联络开关有4个，其备用容量的大小关系为s1>s2>s3>s4.根据启发式规则，无法通过闭合s1来实现整区恢复，于是转入分区恢复.经搜索，得到初始可行解为闭合联络开关s1、s2，断开分段开关b2b3.

由候选集生成规则，自愈方案候选集可由以下方案组成：1)2条相邻馈线；2)3条相邻馈线；3)1条相邻馈线和1条次相邻馈线；4)2条相邻馈线和1条次相邻馈线.初始化自愈候选集中所有方案的浓度和受激励程度为0.5.利用式(9)~(11)进行方案评价，得到所有的自愈方案及其对应的浓度和受激励程度如表 1所示.根据表 1可知，方案1的浓度和受激励程度最高，所以方案1是该故障环境下对应的最优自愈方案.

表 1 自愈方案及其评价 Table 1 Self-healing schemes and evaluations
自愈方案 开关动作次数 网络损耗/kW 受激励程度 方案浓度
闭合s1、s2，断开b1-b2 3 13.445 0.823 5 0.580 2
闭合s1、s3，断开b2-b4 3 16.500 0.518 9 0.504 7
闭合s1、s4，断开b1-b7 3 15.176 0.651 2 0.537 7
闭合s1、s2、s3，断开b1-b7和b2-b4 5 7.208 0.750 6 0.562 3
闭合s1、s2、s4，断开b1-b7和b8-b10 5 9.333 0.476 8 0.494 2
闭合s1、s3、s4，断开b2-b4和b7-b8 5 9.982 0.470 5 0.492 6
闭合s3、s5，断开d1-d7 3 19.670 0.201 8 0.425 9
闭合s4、s5，断开e1-e2 3 24.887 -0.319 9 0.305 8
闭合s1、s3、s5，断开b2-b4和d9-d10 5 15.692 -0.100 4 0.354 2
闭合s1、s4、s5，断开b7-b8和e3-e4 5 14.982 -0.036 5 0.369 0
表选项
5 结论

电网发生故障后，利用启发式规则可以快速得到可行的自愈方案，并结合候选集生成规则确定自愈方案候选集.基于人工免疫动力学模型提出的方案评价方法，能够综合评价候选集中自愈方案对电网的恢复程度，从而确定当前状态下电网的最优自愈策略.仿真算例表明，本文提出的算法能够快速、有效地实现配电网的多目标自愈，为配电网故障后的恢复决策提供参考.

参考文献
[1] 杨德昌, 李勇, ChristianRethanz, 等. 智能输电系统在中国的发展[J]. 电网技术, 2010, 34(5): 1–6.
Yang Dechang, Li Yong, Christian Rethanz. Overview of smart transmission system in China[J]. Power System Technology, 2010, 34(5): 1–6.
[2] 张东霞, 姚良忠, 马文媛. 中外智能电网发展战略[J]. 中国电机工程学报, 2013, 33(31): 1–14.
Zhang Dongxia, Yao Liangzhong, Ma Wenyuan. Development strategies of smart grid in China and abroad[J]. Proceedings of the CSEE, 2013, 33(31): 1–14.
[3] 王珣, 刘亚新, 邓春, 等. 智能输电网分析管控系统开发与应用[J]. 中国电机工程学报, 2011, 31: 50–54.
Wang Xun, Liu Yaxin, Deng Chun, et al. Study and application of smart transmission grid analysis-control system[J]. Proceedings of the CSEE, 2011, 31: 50–54.
[4] 董旭柱, 黄劭远, 陈柔依, 等. 智能配电网自愈控制技术[J]. 电力系统自动化, 2012, 36(18): 17–21.
Dong Xuzhu, Huang Shaoyuan, Chen Rouyi. Network self-healing control technology of smart distribution grid[J]. Automation of Electric Power Systems, 2012, 36(18): 17–21.
[5] Pere Guerrero R, Heydt G T, Jack N J. Optimal restoration of distribution systems using dynamic programming[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 1589–1596.
[6] 张利民, 马强, 李振坤, 等. 基于禁忌克隆遗传算法的配电网故障恢复重构[J]. 电力系统及其自动化学报, 2010, 2(1): 60–64.
Zhang Limin, Ma Qiang, Li Zhenkun. Service restoration reconfiguration in distribution network based on tabu clonal genetic algorithm[J]. Proceedings of CSU-EPSA, 2010, 2(1): 60–64.
[7] 程改红, 徐政. 基于粒子群优化的最优负荷恢复算法[J]. 电力系统自动化, 2007, 31(16): 62–65.
Cheng Gaihong, Xu Zheng. Optimal load recovery algorithm based on particle swarm optimization[J]. Automation of Electric Power Systems, 2007, 31(16): 62–65.
[8] 荀嘉嘉, 黄少先. 基于免疫原理的蚁群算法在配电网恢复中的应用[J]. 电力系统保护与控制, 2008, 36(17): 28–31.
Xun Jiajia, Huang Shaoxian. Ant colony algorithm based on immune principle for the fault restoration of distribution network[J]. Power System Protection and Control, 2008, 36(17): 28–31.
[9] 周勇, 周泉, 刘育民, 等. 基于启发式搜索和模糊评价的配电网故障恢复[J]. 重庆大学学报, 2010, 34(7): 103–108.
Zhou Yong, Zhou Quan. Heuristic research and fuzzy evaluation for-post-fault restoration in distribution networks[J]. Journal of Chongqing University, 2010, 34(7): 103–108.
[10] 赵璇. 智能配电网自愈策略研究[D]. 沈阳: 沈阳理工大学, 2012.
Zhao Xuan. Study on Self-healing Control Method of Smart Distribution Network[D]. Shengyang:Shengyang Ligong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10144-1013140847.htm
[11] 闵波. 基于独特性网络的人工免疫模型研究与应用[D]. 成都: 电子科技大学, 2010.
Min Bo. Artificial immune network and application based on a unique model[D]. Chengdu:UESTC, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10614-2010234025.htm
[12] 高云园. 基于生物免疫机理的多机器人协作研究[D]. 杭州: 浙江大学, 2007.
Gao Yunyuan. Multi-robot collaborative research based on biological immune mechanism[D]. Hangzhou:Zhejiang University, 2007.
[13] 王兆宇, 艾芊. 基于QPSO和BPSO算法的动态微电网多目标优化自愈[J]. 电网技术, 2012, 36(10): 23–29.
Wang Zhaoyu, Ai Qian. Multi-objective optimal self-healing of dynamic microgrid based on QPSO and BPSO[J]. Power System Technology, 2012, 36(10): 23–29.
[14] 臧天磊, 钟佳辰, 何正友, 等. 基于启发式规则和熵权理论的配电网故障恢复[J]. 电网技术, 2012, 35(6): 251–257.
Zang Tianlei, Zhong Jiachen, He Zhengyou. Service restoration of distribution network based on heuristic rules and entropy weight[J]. Power System Technology, 2012, 35(6): 251–257.
[15] 刘育民. 配电网故障诊断与快速供电恢复算法研究[D]. 重庆: 重庆大学, 2006.
Liu Yumin. Study on fault diagnosis and fast service restoration of distribution system[D]. Chongqing:Chongqing University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10611-2006148689.htm