文章信息
- 王毅, 周伟, 张超, 常晓林, 郭华伟
- WANG Yi, ZHOU Wei, ZHANG Chao, CHANG Xiaolin, GUO Huawei
- 基于热流管单元的混凝土通风冷却效果
- Concrete cooling effect by air cooling based on heat-fluid pipe element
- 武汉大学学报 (工学版), 2017, 50(1): 50-57
- Engineering Journal of Wuhan University, 2017, 50(1): 50-57
- http://dx.doi.org/10.14188/j.1671-8844.2017-01-007
-
文章历史
- 收稿日期: 2016-06-05
2. 长江勘测规划设计研究院,湖北 武汉 430015
2. Changjiang Institute of Survey, Planning, Design and Research, Wuhan 430015, China
大体积混凝土浇筑后,混凝土中的水泥水化反应释放大量的热量,由于混凝土导热能力差,其温度不断升高,后期随着混凝土温度逐渐降低,弹性模量逐渐增强,混凝土拉应力不断增大,如果其拉应力值大于抗拉强度极限时,混凝土就会产生裂缝.此外,在上述温度变化过程中均伴有内外温差,较大的内外温差也是大体积混凝土开裂的主要原因.国内外在建或已建成的众多大体积混凝土建筑物均或多或少地出现了温度裂缝,由此可见,温控防裂在大体积混凝土结构中是十分重要的.我国目前大体积混凝土温控措施中最常使用的是使用内嵌水管通水冷却来降低混凝土温度.但该工程措施在较为干旱的地区实施起来较为困难,而且在实际工程中,由于建筑物较高、水压不足所导致混凝土最高温度超标的情况也可能会发生,除此之外,在部分高寒地区,水易结冰,施工过程中不宜采取通水冷却,而采用通风冷却能够很好地避免上述的诸多问题,且相较于水,空气密度较小,可采用竖直方向通风冷却.
我国风冷主要应用于混凝土前期骨料预冷,国内外对于浇筑过程中采用通风冷却的研究较少.我国澳门银河娱乐度假酒店修建过程中采用了混凝土通风冷却,张勇[1]通过该工程实例验证了空气冷却大体积混凝土的可行性与有效性.Hedlund、Groth[2-3]在20世纪末进行了通风冷却的物理实验,并将其实验结果应用于格斯塔港大桥的数值模拟,模拟结果与实测值基本一致,由此证明了其实验结果的可靠性,并在后续仿真计算中证明了空气冷却在混凝土墙体结构中应用的可行性.Ishikawaet[4]等人提供了一套实际工程中局部冷却的空气冷却系统.Miguel Azenha[5]等人通过帕拉德拉坝闸墩的原型实测、物理实验以及数值仿真验证了空气冷却在大体积碾压混凝土闸墩中应用的可行性以及其对于预防早龄期混凝土开裂的有效性.
由于空气比热较小,其温度在通风管道的沿程变化不能忽略,因此为了更真实地模拟空气冷却效果,本文利用热流耦合管单元法[6-12]进行仿真计算,充分考虑空气在通风管道内的沿程温升,对通风冷却效果的影响因素进行敏感性分析,对比通水冷却及通风冷却的冷却效果,并从中得出一些结论,为工程实际中混凝土通风冷却提供参考.
1 计算原理大体积混凝土空气冷却过程中混凝土为一不稳定温度场,根据热学问题的基本理论,不稳定温度场应满足如下偏微分方程:
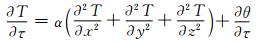 (1)
(1)
其中:T为温度;α为材料的导热系数;θ为材料的绝热温升.
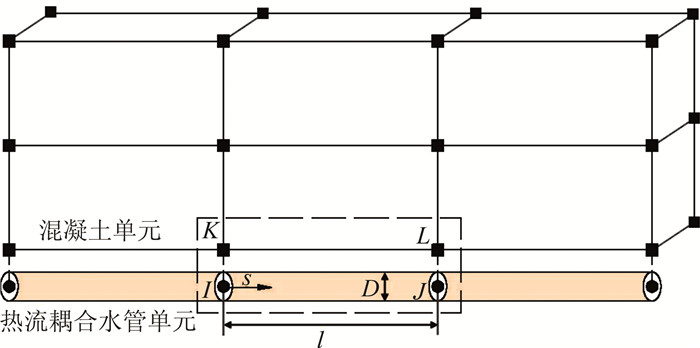
1.1 热流耦合精细算法空气对混凝土的冷却问题与通水冷却相同,是一个空间温度场问题,即混凝土中的热量由于混凝土与空气之间的温差传递到空气中,并随着空气的流动被带走.混凝土空气冷却效果分析考虑将通入管道中的空气视作一维恒定流,采用热流耦合单元,充分考虑管道内空气的流动、传热以及与混凝土的对流,精细考虑水管附近温度随时间及通气的变化情况.空气冷却的仿真分析中,混凝土采用三维实体单元离散,通风管道采用热流管单元离散.如图 1~2,热流管单元采用4节点建立,其中2节点 (I、J) 为水管单元节点,另外2节点 (K、L) 为水管附近混凝土节点,通过相应节点处的耦合完成空气与混凝土之间的热对流,并在计算过程中随着热量被空气带走,考虑气温的沿程变化.
|
| 图 1 热流管单元热交换原理 Figure 1 Heat exchange of coupled thermal-fluid pipe |
|
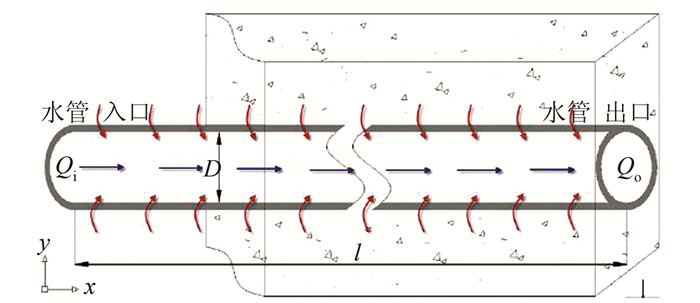
| 图 2 水管冷却热量交换机制 Figure 2 Mechanism of heat transfer with internal flow |
热流管单元与混凝土单元的热交换过程根据能量守恒可表达为如下方程:
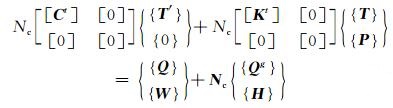 (2)
(2)
式中:[Ct]为比热矩阵;[T′]为节点变温速率向量;[Kt]为热传导矩阵;{T}为节点温度向量;{P}为节点应力向量;{Q}为节点热流向量;{W}为节点流体向量;{Qg}为热生向量; {H}为重力效应向量;Nc为平行管道数.
本文在热流耦合精细算法中不同冷却介质与混凝土的对流热传导系数均采用Dittus-Boelter[13]方程确定:
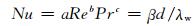 (3)
(3)
式中:Nu为努塞尔特数;Re为雷诺数;Pr为普兰特数;β为混凝土与冷却介质之间的对流热传导系数;λw为冷却介质的导热系数;d为管径.
通水冷却采用McAdams[14]建议的a=0.023, b=0.8, 加热时c=0.4,冷却时c=0.3.通风冷却采用Hedlund、Groth[2]试验结果拟合值进行计算,如图 3所示,拟合值a=0.007, b=0.907, c=0.33.
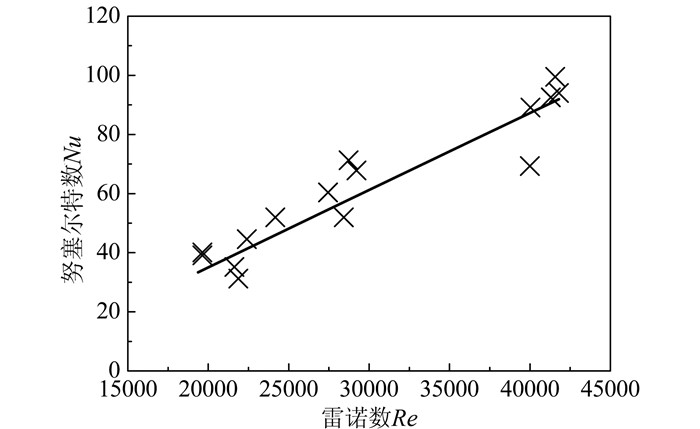
|
| 图 3 通风冷却Dittus-Boelter方程拟合值 Figure 3 Fitting values of Dittus-Boelter equation by air cooling |
将通风冷却与混凝土接触等效为第三类边界条件.第三类边界条件假定混凝土表面与流体之间的热流量与接触面温度和流体温度之差成正比[15],即:
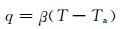 (4)
(4)
式中:q为热流量;β为混凝土与冷却介质之间的对流热传导系数;T为混凝土表面温度;Ta为流体温度.
混凝土与风之间的对流热传导系数采用Hedlund、Groth[2]试验结果,如图 4所示.
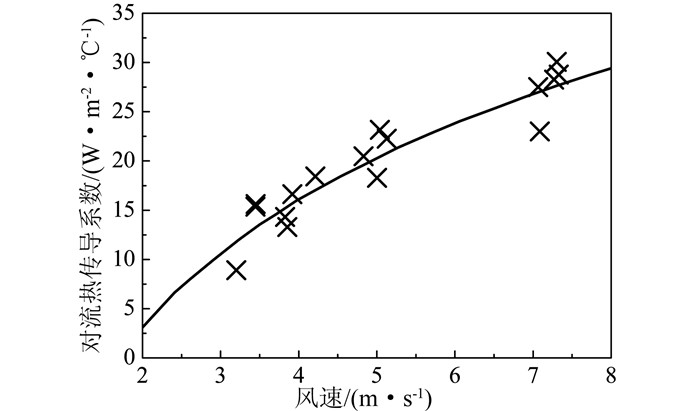
|
| 图 4 通风冷却对流热传导系数 Figure 4 Heat transfer coefficient of air cooling |
Hedlund、Groth[3]将通风管与混凝土接触面等效为第三类边界条件,对混凝土结构某一截面进行仿真分析,结果表明,已知某一截面通风温度、风速及该风速下空气与混凝土的对流热传导系数的情况下,可以较为准确地计算出该截面混凝土温度场.为保证热流耦合精细算法的准确性,笔者采用热流耦合精细算法对某一混凝土截面进行通风冷却计算.以混凝土单元各节点平均温度作为对比衡量标准.
模型截面尺寸为1.5 m×1.5 m,混凝土厚0.1 m.对流边界条件等效为第三类边界条件及热流耦合精细算法混凝土材料采用八节点Solid70离散,热流耦合精细算法中冷却管采用Fluid116热流耦合管单元进行离散.网格划分见图 5.混凝土块四周设置绝热.通风管径为90 mm,风速为5 m/s,通风温度为12 ℃.

|
| 图 5 冷却管附近网格划分 Figure 5 Element mesh around the cooling pipe |
混凝土的绝热温升公式按复合指数型公式进行拟合:
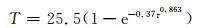 (5)
(5)
| 导温系数 /(m2·h-1) |
导热系数/(kJ· m-1·h-1·℃-1) |
比热/(kJ· kg-1·℃-1) |
| 0.004 | 9.80 | 1.02 |
| 密度 /(kg·m-3) |
导热系数/(J· m-1·s-1· ℃-1) |
比热/(kJ· kg-1·℃-1) |
流体黏度 /(10-5Pa·s) |
| 1.29 | 0.023 | 1.005 | 1.81 |
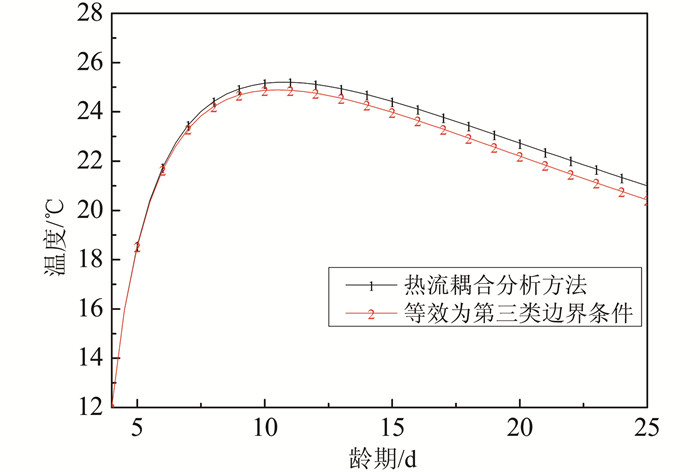
根据上述条件进行仿真计算,结果如图 6所示.
|
| 图 6 仿真结果对比 Figure 6 Simulation results contrast |
由图 6可知,采用热流耦合分析方法计算得到的混凝土通风冷却效果与将通风过程等效为第三类边界条件时计算所得的冷却效果基本一致;由于本文将通风过程等效为第三类边界条件时,未考虑冷却空气沿程温度上升导致混凝土与冷却空气热交换效果的降低,因而此方法计算的整个混凝土块平均温度比热流耦合分析方法所得的结果偏低.从冷却效果来看,考虑了冷却介质沿程温升的热流耦合分析方法更能准确反映混凝土浇筑块内的温度变化情况.
3 通风冷却效果敏感性分析不同实际工程对于混凝土的温度控制要求有所不同,即使同一工程也可能由于混凝土所在位置的不同而制定不同的温控标准.笔者采用第2节中混凝土截面有限元模型,运用热流耦合精细算法,对通风冷却中冷却风速、通风温度及混凝土截面尺寸进行敏感性分析,为实际工程选择合适的冷却方案提供借鉴.在不同影响因素的敏感性分析中均以混凝土单元各节点平均温度作为冷却效果衡量标准,混凝土浇筑温度均为12 ℃,通风管管径均采用90 mm.
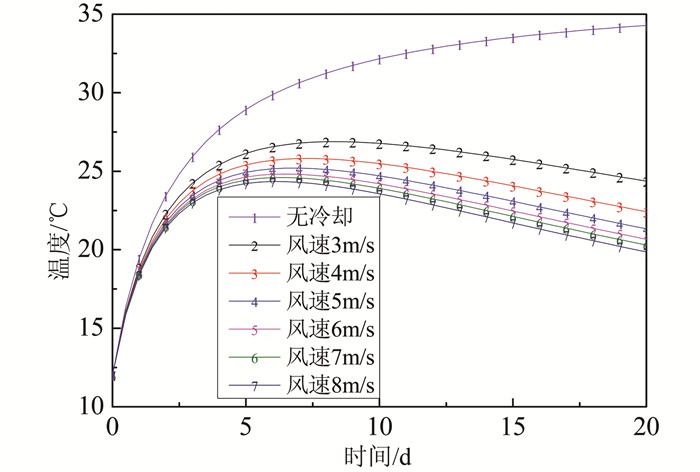
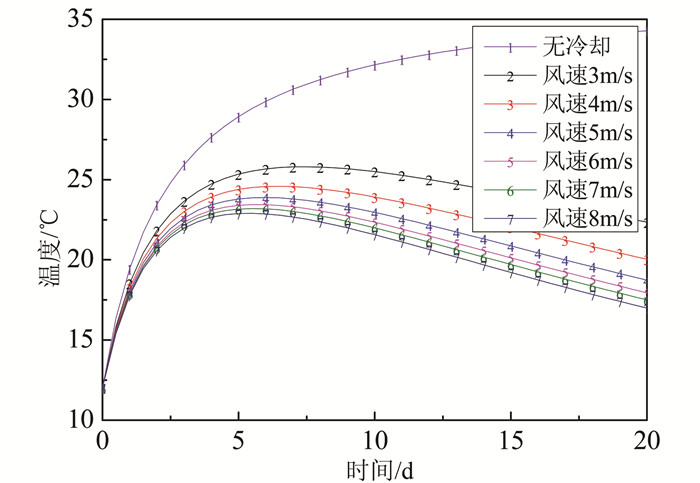
3.1 冷却风速敏感性分析由于空气的密度较小,因此单位体积带走的热量有限,为了保证混凝土的冷却效果必须要采用较大通风流量,在此以通风风速作为变量.计算风速在3~8 m/s时,不同风速的冷却效果.计算过程中选取两个不同的通风温度8 ℃、12 ℃,混凝土截面大小为1.5 m×1.5 m.仿真结果如图 7~8所示.
|
| 图 7 混凝土平均温度 (风温12 ℃) Figure 7 Concrete average temperature (Air temperature is 12 ℃) |
|
| 图 8 混凝土平均温度 (风温8 ℃) Figure 8 Concrete average temperature (Air temperature is 8 ℃) |
由图 7可知,混凝土浇筑后,前期水化热大量释放,释放的水化热多于风冷带走的热量,致使混凝土温度不断升高;随着时间的增长,水化热释放逐渐减小,风冷带走的热量多于水化热的释放量,混凝土温度逐渐降低.仿真计算结果显示,不同的风速条件下,通风冷却均能够较为有效地削减混凝土温度曲线的峰值.
同一通风温度条件下,随着风速的增大,通风流量增大,相应能够带走更多的热量,混凝土温度逐渐降低,冷却效果更好.在同一时间,风速每增加1 m/s,混凝土与风之间对流热传导系数的增幅逐渐降低,混凝土温度曲线是逐渐收敛的.在风速大于5 m/s时,其敏感性随着风速的增大而不断减弱.不同工程实际所需混凝土的降温幅度各有不同,因此可针对实际所需温度降幅选择合适的通风速度,本文推荐采用5 m/s左右的通风速度进行冷却.
由图 7、图 8对比可知,不同通风温度条件下,不同风速混凝土温度的变化规律基本一致.但当风速为6~8 m/s时,通风温度为8 ℃各温度曲线之间同一时刻的差值均大于通风温度为12 ℃的差值,由此可知,随着通风温度的降低,风速的敏感性增强.
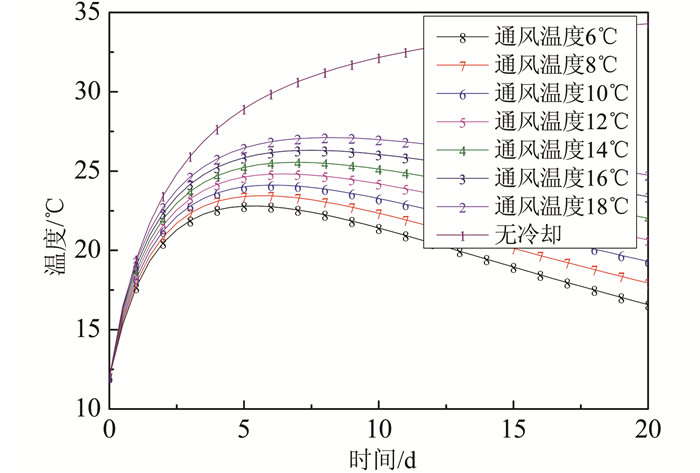
3.2 风冷温度敏感性分析选取6~18 ℃不同的通风温度进行敏感性计算,仿真计算中混凝土截面尺寸为1.5 m×1.5 m,风速为5 m/s.仿真结果如图 9~10所示.
|
| 图 9 混凝土平均温度 Figure 9 Concrete average temperature |
|
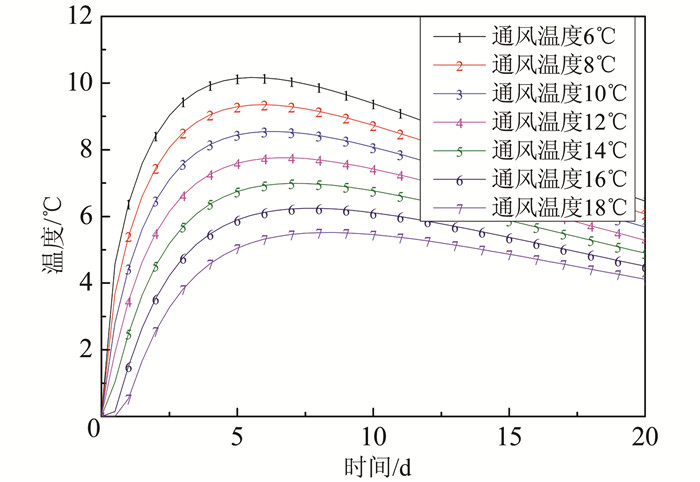
| 图 10 混凝土截面温差 Figure 10 Temperature difference of concrete cross-section |
由图 9可知,不同通风温度条件下混凝土平均温度的变化规律基本一致.通风温度在6~18 ℃时,通风冷却对混凝土均有较好的削峰效果.而对比不同通风温度混凝土的平均温度历程曲线可知,混凝土平均温度对于通风温度的大小有较强的敏感性,随着通风温度的降低,混凝土平均温度明显降低,仅变化通风温度混凝土平均温度峰值基本呈线性变化,通风温度每降低2 ℃,混凝土最高温度降低约0.7 ℃.除此之外,随着通风温度的降低,混凝土平均温度在后期的降温过程中降温速率增大,因此不同通风温度之间混凝土平均温度的差距随着时间的增长而变大,在浇筑20 d时,通风温度每降低2 ℃,混凝土平均温度降低1.4 ℃.
由图 10可知,不同通风温度混凝土截面温差 (某一时刻截面最高温度与最低温度差值) 变化规律基本一致,在混凝土平均温度与截面温差在同一时刻达到最大值.对比不同通风温度混凝土截面温差曲线可知,在同一时刻,随着通风温度的降低,混凝土截面温差增大,这主要是由混凝土本身热阻导致的,即靠近通风管的混凝土由于通风温度较低而导致其温度值较低,而远离通风管的混凝土受到通风温度的影响较小,从而导致其混凝土截面温差增大,通风温度每降低2 ℃,混凝土截面最大温差增加0.8 ℃左右.混凝土截面温差达到峰值后,通风温度越高,后期截面温差变化越小,在20 d时,不同通风温度混凝土截面温差在4~6 ℃,通风温度每降低2 ℃,混凝土截面温差增加0.36 ℃左右.
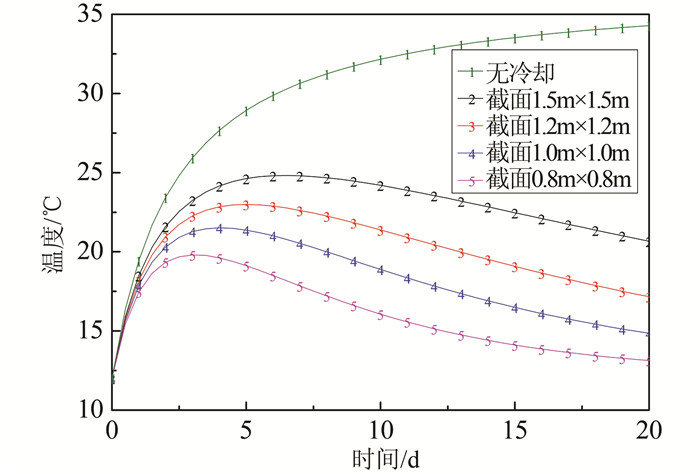
3.3 混凝土截面大小敏感性分析在混凝土截面大小敏感性分析中,笔者选取4种混凝土截面,分别为1.5 m×1.5 m、1.2 m×1.2 m、1.0 m×1.0 m以及0.8 m×0.8 m,不同截面尺寸风速为5 m/s,通风温度为12 ℃.仿真结果见图 11~12.
|
| 图 11 混凝土平均温度 Figure 11 Concrete average temperature |
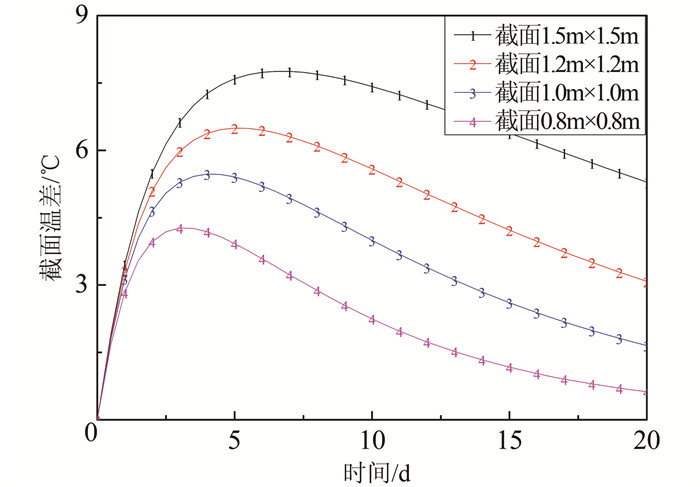
|
| 图 12 混凝土截面温差 Figure 12 Temperature difference of concrete cross-section |
由图 11可知,通风冷却均能够有效地削减不同截面大小混凝土温度峰值.随着截面尺寸的减小,在相同的通风条件下,其冷却效果越来越好.截面0.8 m×0.8 m增大至1.0 m×1.0 m时,混凝土最高温度升高1.7 ℃,在20 d时,混凝土平均温度升高1.6 ℃;截面1.0 m×1.0 m增大至1.2 m×1.2 m时,混凝土最高温度升高1.5 ℃,在20 d时,混凝土平均温度升高2.2 ℃;截面1.2 m×1.2 m增大至1.5 m×1.5 m时,混凝土最高温度升高1.8 ℃,在20 d时,混凝土平均温度升高3.5 ℃.
由图 12可知,通风冷却中,混凝土截面温差与平均温度在同一时刻达到最大值,之后会随着时间增长,截面温差不断减小.对比不同截面尺寸的混凝土温差曲线可知,在相同的通风冷却条件下,截面越小,混凝土的温差越小,且在截面温差达到峰值后,温差降低的速率加快.
4 不同冷却介质冷却效果对比 4.1 计算模型及参数混凝土内嵌水管通水冷却是当前我国最常采用的混凝土冷却措施之一,众多的工程实际也验证了该法的可行性与有效性,因此笔者将通水冷却的冷却效果作为一个评判标准来判断空气冷却能否达到相似的冷却效果.由于空气和水的密度、比热以及与混凝土之间的对流热传导系数均存在较大差异,在计算中是无法获取完全相同的温度场的,因此本文以通水冷却、通风冷却混凝土单元各节点平均温度作为参考.仿真计算中混凝土的浇筑温度为12 ℃,水管管径32 mm,通水流量1.5 m3/h,通水20 d,冷却水水温为14 ℃.
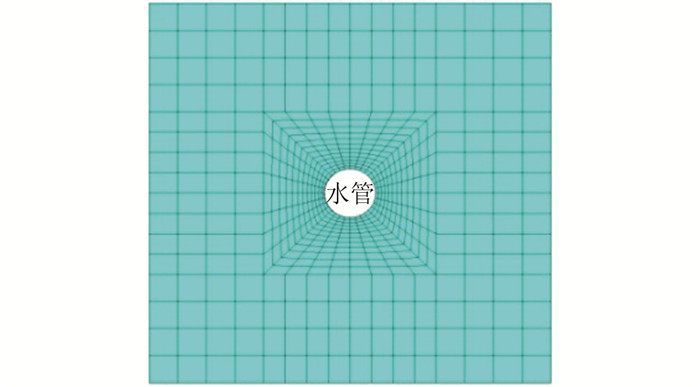
为了方便研究,计算模型为一混凝土块,如图 13~14所示,模型截面尺寸为1.5 m×1.5 m,垂直截面方向长20 m,混凝土块体积约为45 m3.混凝土材料采用八节点Solid70实体单元离散,冷却管采用Fluid116热流耦合管单元进行离散.混凝土块四周均进行绝热设置.

|
| 图 13 计算模型 Figure 13 Calculation model |
|
| 图 14 冷却管附近网格划分 Figure 14 Element mesh around cooling pipe |
混凝土和空气的热力学参数见表 1~2,冷却水热学参数见表 3.
| 密度 /(kg·m-3) |
导热系数/(J/ m-1·s-1· ℃-1) |
比热/(kJ· kg-1·℃-1) |
流体黏度 /(10-3Pa·s) |
| 1 000 | 0.58 | 4.183 | 1.1 |
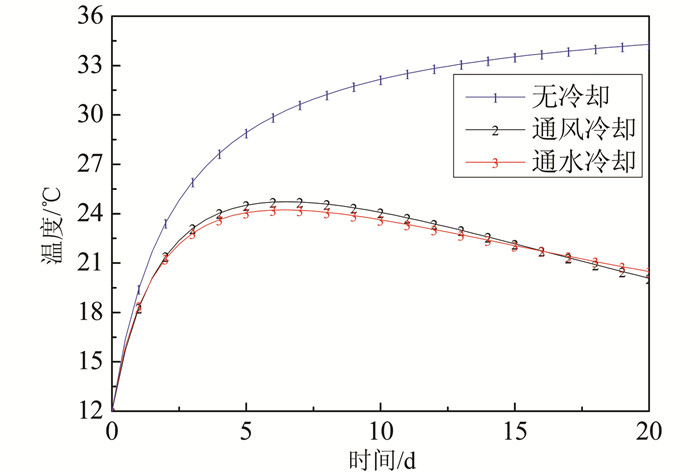
选取通风管管径90 mm,风速8 m/s,通风温度6.5 ℃,经过计算可知,在该条件下通风冷却所得混凝土整体平均温度与4.1中所述通水条件下所得混凝土平均温度基本一致,如图 15所示.
|
| 图 15 混凝土平均温度 Figure 15 Concrete average temperature |
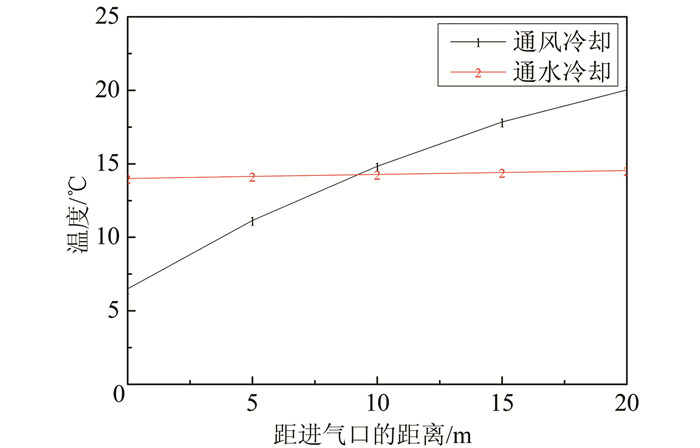
由图 16可知,相较于冷却水,冷却空气的密度及比热极小,在吸收相同热量的条件下,冷却空气升温幅度远大于冷却水;在冷却管长为20 m条件下,整个冷却过程中,冷却水进、出口水温最大温度变化为0.5 ℃;冷却空气进、出口最大温度变化为13 ℃.由于空气温度变化较快,空气冷却效果会随着管长的增大而快速减弱,因此混凝土通风冷却的适用跨度、管道布置形式以及通风方式还有待进一步研究.
|
| 图 16 冷却管不同位置冷却介质最高温度 Figure 16 Highest temperature along cooling pipe |
由于水温沿程基本无变化,因此在冷却水入口截面与出口截面处的混凝土温度场基本一致,相较于通水冷却,风温度沿程变化较快,风入口与出口截面处混凝土的温度场变化较大.
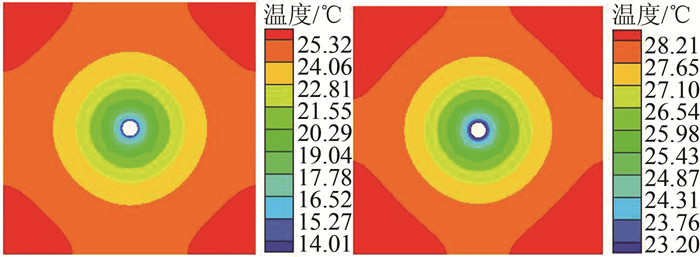
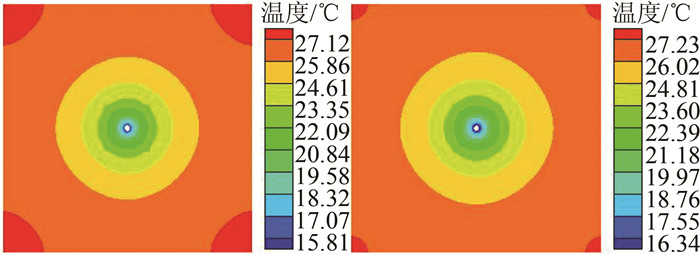
图 17~18为冷却介质进口与出口处混凝土截面温差最大时刻的温度场.通水冷却不同截面内部最大温差发生在混凝土温度峰值所处的时刻即浇筑后6 d左右,入口与出口截面最大温差均为11 ℃左右.空气冷却混凝土截面最大温差也与该截面节点温度峰值所处的时刻相同,但由于空气温度的沿程变化较大,不同截面内节点温度达到峰值的时间有所不同,入口截面处混凝土最大温差发生在浇筑后4 d,最大温差11.3 ℃,出口截面最大温差发生在浇筑后8.5 d左右,最大温差为5.0 ℃.由此可知,不同冷却方法的混凝土截面温度梯度均较大,但在相似冷却效果条件下,相较于冷却通水,通风冷却截面温度梯度较小.
|
| 图 17 通风入口与出口混凝土截面温度分布 Figure 17 Temperature distribution of inlet and outlet cross-section of air cooling |
|
| 图 18 冷却水入口与出口混凝土截面温度分布 Figure 18 Temperature distribution of concrete cross-section at inlet and outlet of water cooling pipe |
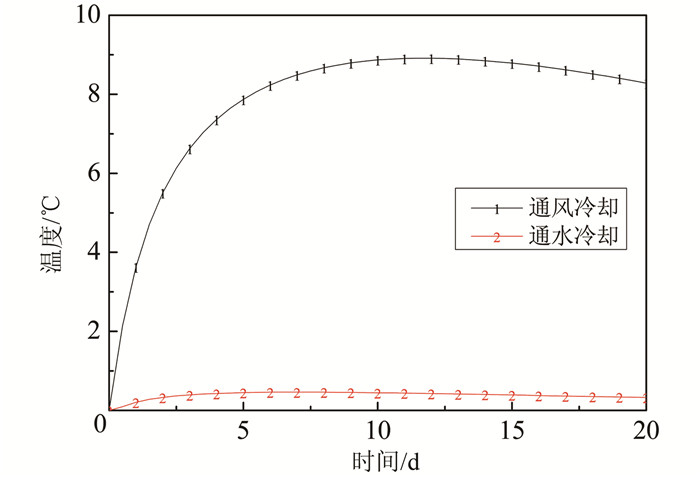
由图 19可知,由于水温沿程变化较小,因此水管附近混凝土不同点的温度历程曲线相差较小,整个冷却过程中,沿冷却水管方向水管附近点温差最大值与混凝土温度峰值发生的时刻相同 (浇筑第6 d),最大温差为0.53 ℃.相较于冷却通水,空气温度沿程升高较快,通风管附近点的温度历程曲线变化较大.而与冷却通水不同的是,沿通风管方向最大温差未出现在混凝土温度达到峰值的时刻附近,而是发生在浇筑过后11 d左右,最大温差为8.9 ℃.远离冷却管处混凝土与冷却管附近混凝土的温度变化规律一致.由此可知,空气冷却在沿冷却管方向上混凝土的温度梯度要远大于冷却通水的温度梯度,但远小于截面温度梯度.
|
| 图 19 冷却管附近混凝土沿管方向温差 Figure 19 Temperature difference of concrete along water cooling pipes |
本文对比了混凝土通水冷却及通风冷却的冷却效果,并进行了通风冷却不同影响因素的敏感性分析,仿真结果表明:
1) 不同通风条件的通风冷却能够较为有效地削减混凝土温度峰值.随着风速的增大,混凝土平均温度对风速的敏感性逐渐降低,建议在实际工程中采用5 m/s左右的冷却风速.相较于通风速度,混凝土平均温度对通风温度、混凝土截面尺寸的敏感性较强.通风温度每降低2 ℃,混凝土平均温度最大值降低0.7 ℃左右,混凝土截面温差最大值约增大0.8 ℃.混凝土平均温度及混凝土截面温差均随着截面面积的减小而减小.
2) 以混凝土平均温度变化过程作为混凝土冷却效果的评判标准,通风冷却能够达到与通水冷却相似的冷却效果.在相似冷却效果前提下,通风冷却及通水冷却均会使混凝土截面产生较大温度梯度,通风冷却混凝土截面温度梯度小于通水冷却;沿冷却管方向,通风冷却混凝土温度梯度远大于通水冷却,但该梯度远小于截面温度梯度.
3) 通风冷却中风温沿通风管道方向温升幅度较大,因此混凝土通风冷却的适用跨度、管道布置形式以及通风方式还有待进一步的研究.
| [1] |
张勇. 大体积混凝土风冷却技术研究与应用[J].
中国建设信息, 2010(7): 81–83.
Zhang Yong. Research and application of mass concrete air cooling technology[J]. Information of China Construction, 2010(7): 81–83. |
| [2] | Hedlund H, Groth P. Air cooling of concrete by means of embedded cooling pipes-Part Ⅰ: Laboratory tests of heat transfer coefficients[J]. Materials and Structures, 1998, 31(5): 329–334. DOI:10.1007/BF02480675 |
| [3] | Groth P, Hedlund H. Air cooling of concrete by means of embedded cooling pipes-Part Ⅱ: Application in design[J]. Materials and Structures, 1998, 31(6): 387–392. DOI:10.1007/BF02480711 |
| [4] | Ishikawa S, Matsukawa K, Nakanishi S, et al. Air pipe cooling system[J]. Concrete International, 2007, 29: 45–49. |
| [5] | Azenha M, Lameiras R, de Sousa C, et al. Application of air cooled pipes for reduction of early age cracking risk in a massive RC wall[J]. Engineering Structures, 2014, 62: 148–163. |
| [6] |
段寅, 向正林, 常晓林, 等. 大体积混凝土水管冷却热流耦合算法与等效算法对比分析[J].
武汉大学学报 (工学版), 2010, 43(6): 703–707.
Duan Yin, Xiang Zhengling, Chang Xiaolin, et al. Comparative analysis of pipe cooling in mass concrete using thermal fluid coupling method and equivalent method based on FEM[J]. Engineering Journal of Wuhan University, 2010, 43(6): 703–707. |
| [7] |
闫慧玉.大体积混凝土温度场水管冷却热流耦合仿真方法研究[D].武汉:武汉大学, 2005.
Yan Huiyu. Study on thermal-fluid method of water pipe cooling for the temperature field of mass concrete[D]. Wuhan: Wuhan University, 2005. |
| [8] |
刘杏红, 马刚, 常晓林, 等. 基于热-流耦合精细算法的大体积混凝土水管冷却数值模拟[J].
工程力学, 2012, 29(8): 159–164.
Liu Xinghong, Ma Gang, Chang Xiaolin, et al. The refined numerical simulation of pipe cooling in mass concrete based on heat-fluid coupling method[J]. Engineering Mechanics, 2012, 29(8): 159–164. |
| [9] | Liu X, Duan Y, Zhou W, et al. Modeling the piped water cooling of a concrete dam using the heat-fluid coupling method[J]. Journal of Engineering Mechanics, 2012, 139(9): 1278–1289. |
| [10] |
李梁, 张超, 张振洲, 等. 基于热流管单元的大体积混凝土一期冷却效果精细模拟[J].
武汉大学学报 (工学版), 2013, 46(4): 442–448.
Li Liang, Zhang Chao, Zhang Zhenzhou, et al. Refined simulation of first stage artificial cooling effect in mass concrete based on heat-fluid pipe element[J]. Engineering Journal of Wuhan University, 2013, 46(4): 442–448. |
| [11] |
刘俊, 黄玮, 周伟, 等. 大体积混凝土小温差的长期通水冷却[J].
武汉大学学报 (工学版), 2011, 44(5): 549–553.
Liu Jun, Huang Wei, Zhou Wei, et al. Study of small temperature difference and long-term water cooling in mass concrete[J]. Engineering Journal of Wuhan University, 2011, 44(5): 549–553. |
| [12] | Liu Xinghong, Zhang Chao, Chang Xiaolin, et al. Precise simulation analysis of thermal field in mass concrete with pipe water cooling system[J]. Applied Thermal Engineering, 2015, 78: 449–459. DOI:10.1016/j.applthermaleng.2014.12.050 |
| [13] | Dittus F W, Boelter L M K. Heat transfer in automobile radiators of the tubular type[J]. International Communications in Heat and Mass Transfer, 1985, 12(1): 3–22. DOI:10.1016/0735-1933(85)90003-X |
| [14] | McAdams W H. Heat Transmission[M]. New York: McGraw-Hill, 1954. |
| [15] |
朱伯芳.
大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1999.
Zhu Bofang. Thermal Stresses and Temperature Control of Mass Concrete[M]. Beijing: China Electric Power Press, 1999. |
 2017, Vol. 50
2017, Vol. 50




