文章信息
- 方自虎, 简旭阳, 周尧, 李向鹏
- FANG Zi-hu, JIAN Xu-yang, ZHOU Yao, LI Xiang-peng
- 考虑屈曲的钢筋滞回模型
- Hysteretic model of reinforced bar considering buckling
- 武汉大学学报(工学版), 2016, 49(2): 254-258
- Engineering Journal of Wuhan University, 2016, 49(2): 254-258
- http://dx.doi.org/10.14188/j.1671-8844.2016-02-016
-
文章历史
- 收稿日期: 2015-09-28
钢筋混凝土结构受循环荷载作用的力学性能分析无疑是当前混凝土结构研究的热点之一,其中,循环荷载下混凝土力学性能自然是很多研究者热衷研究的对象.然而钢筋在循环荷载下的力学模型对钢筋混凝土结构数值分析结果的影响也不容忽视,这也引起很多研究者对循环荷载下钢筋的力学性能产生了浓厚兴趣[1-3].特别是文献[1]提出的开创性的M-P模型,对循环荷载钢筋模型的研究起到了巨大的促进作用,引起很多研究者对该模型进行更深入的研究[4-9].文献[4]还针对M-P模型编制了程序放入到开源平台OpenSees中,更进一步促进了研究者对钢筋模型研究的热情.除了对M-P模型的参数取值和单调荷载下钢筋应力应变曲线线形进行研究外,还有研究者在该模型中加入了钢筋受压屈曲后的数值分析方法[5-9],特别是文献[8]采用文献[7]考虑钢筋屈曲的分析方法编制了程序,并将该程序提供给OpenSees以后,极大地促进了研究者对钢筋屈曲的研究.此后,有研究者将考虑屈曲的钢筋模型开发到COSMOS平台上[9].我国有研究者依据CLOUGH[10]分析框架的模型建立起循环荷载钢筋模型,并在商业平台ABAQUS上开发了应用程序[11].
众所周知,由于工程材料使用特点,设计人员使用的钢筋材料特性多数为所在区域的设计规范文件提供,而这类钢筋材料一般仅提供屈服强度和弹性模量,全部的钢筋受拉应力应变关系几乎不可能得到,因此,在工程应用中,单调荷载下二折线的钢筋应力应变关系的应用更加普遍,最常用的即为理想弹塑性钢筋模型.而开源平台OpenSees使用对象为极少数的研究者,使用该平台同时还要具有Tcl计算机语言知识,这更使得该平台一时难以实现在工程中的普遍应用.
鉴于上述情况,本文将文献[3]以单调荷载下三折线钢筋应力应变关系建立的循环荷载钢筋模型,简化为二折线应力应变关系的循环荷载钢筋模型,结合文献[7]钢筋屈曲的技术,建立了考虑屈曲的循环荷载钢筋滞回模型,并在商业平台ABAQUS上进行了二次开发,使得考虑屈曲的钢筋滞回模型可以方便地用于工程设计.通过循环荷载下钢筋混凝土梁和剪力墙3个试验结果的数值分析,验证了本文方法的有效性.
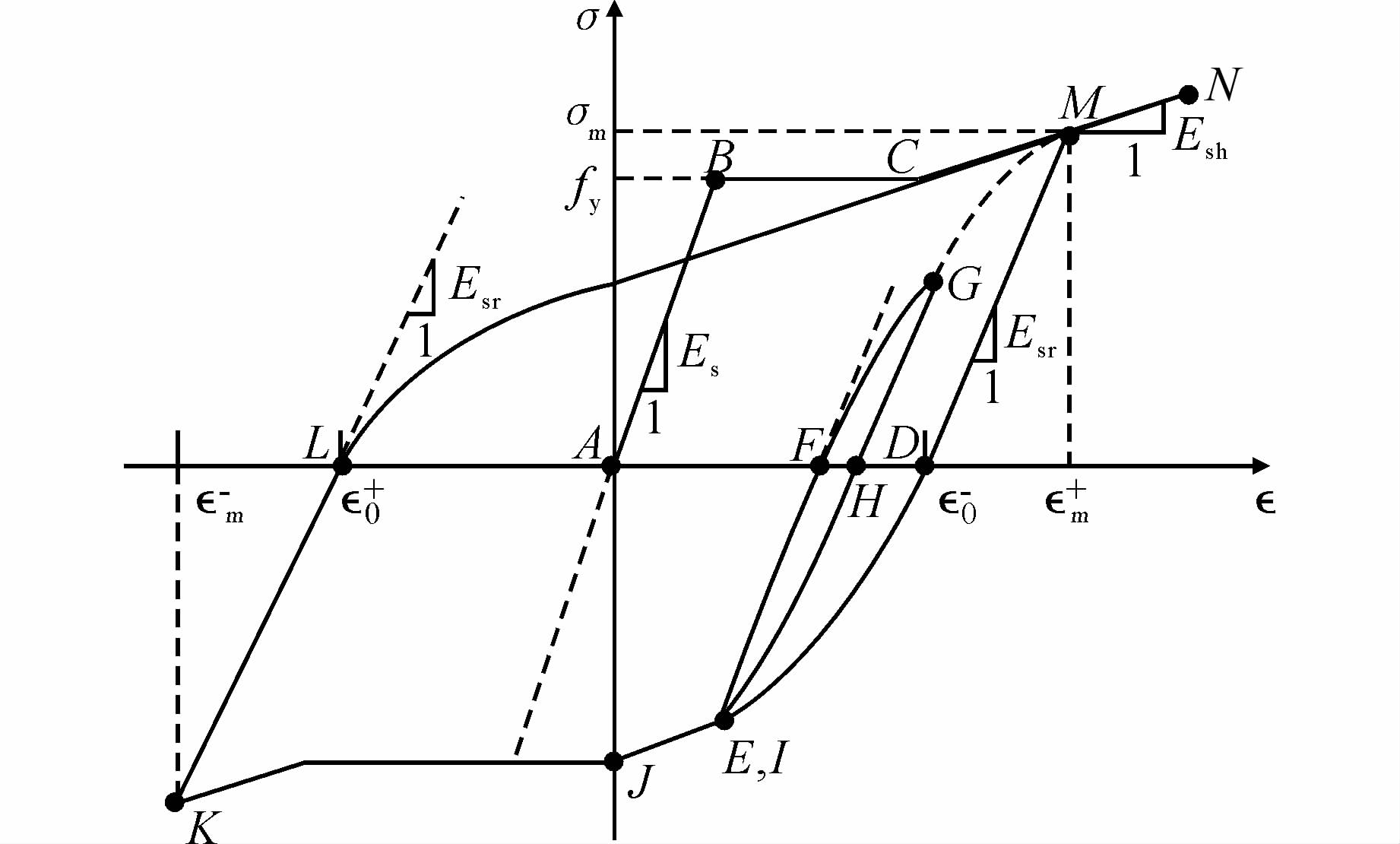
1 VECCHIO钢筋模型Vecchio[3]根据Skckin[12]提出的钢筋模型改编的循环荷载钢筋模型如图 1所示.
图 1中,单调荷载下钢筋应力应变关系假定为三折线,即图中ABCN;初始刚度为Es,屈服应力为fy,经过屈服平台(BC段)后进入线性硬化阶段,硬化刚度为Esh;荷载第一次循环沿单调荷载路径(即三折线),而卸载路径为直线,其刚度为Esr;从应力为零点(ε0,图中上标“+”代表拉应变,“-”代表压应变,最大应变εm同其一致)到该方向最大应变(εm)之间的加载路径(图中LM曲线)由下式确定:
式(1)中的系数N由下式确定:
式(1)是根据Ramberg-Osgood模型建立的,材料的Bauschinger效应已经包含其中,该加载曲线在加载起点刚度等于卸载刚度,而在应变最大点刚度等于硬化刚度.当从正向加载经卸载到第一次负向循环加载时,加载曲线为图中的DJ线段,即负向没有最大应变时,取最大负向应变为0(εm=0).
卸载刚度Esr根据εm-ε0区间的大小而变化.当εm-ε0εy(εy为屈服应变)时,卸载刚度等于初始刚度Es;当εm-ε0>4εy时,卸载刚度取0.85Es;当εy<εm-ε0<4εy时,卸载刚度按照下式计算:
不完全加载与卸载路径如图 1中EFGHI线段.其中EF和GH的卸载段是直线,FG和HI是式(1)确定的曲线.
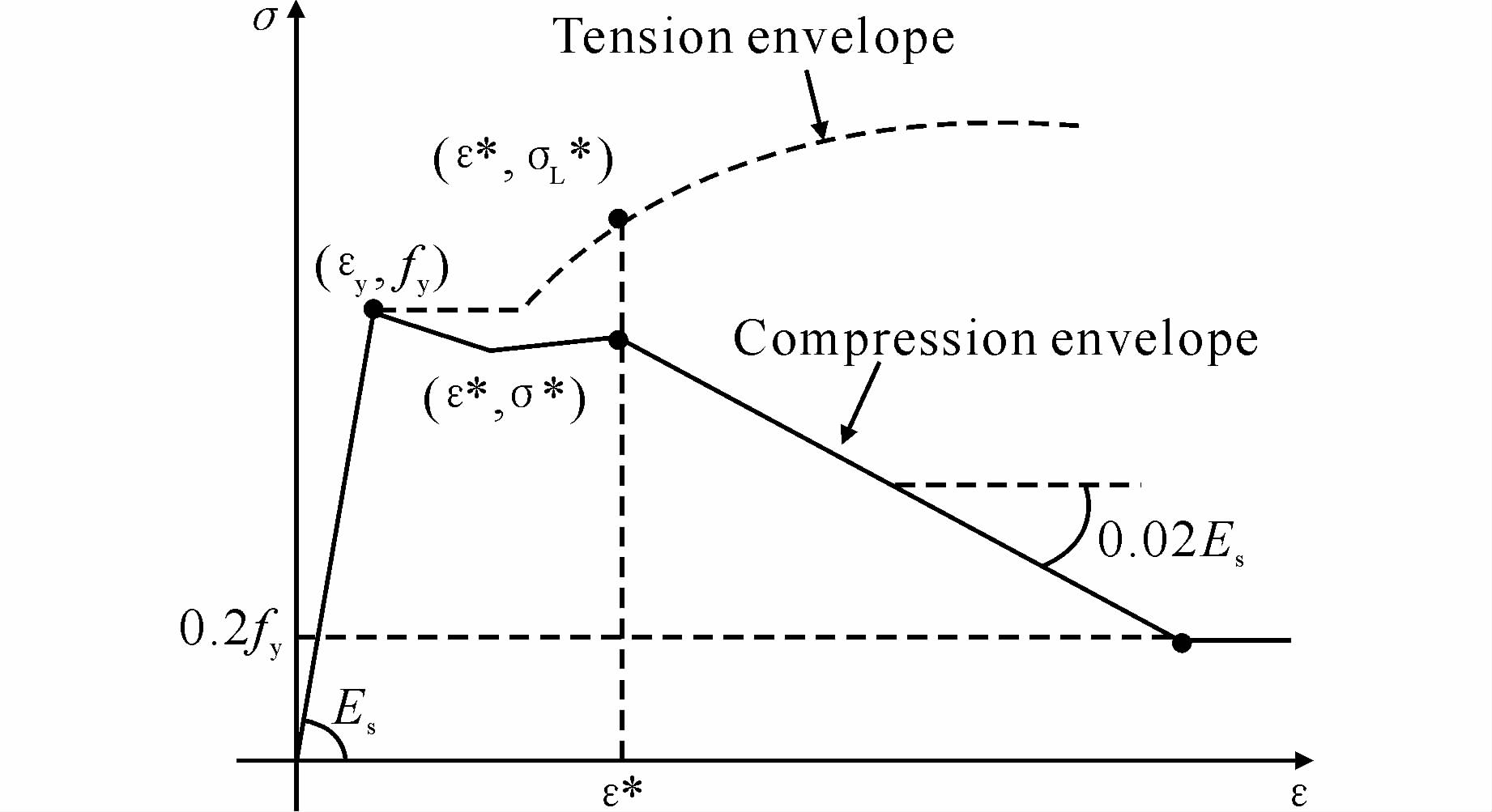
2 屈服效应模型文献[5]在大量的单调和循环荷载下通过三组长细比(L/D,L为钢筋长度,D为钢筋直径)的钢筋试验,发现了钢筋压应力应变曲线与拉应力应变曲线之间的典型特征,文献[7]在分析文献[5]和其他研究者的试验结果以及自己完成的试验结果后,对钢筋单调受压平均应力应变曲线总结出以下规律:1)平均压应力应变曲线仅仅取决于长细比和屈服强度的乘积;2)屈曲后的平均压应力较无屈曲时压应力要小,其变小的规律与无屈曲时的应力应变曲线相关;3)屈曲后期平均压应力应变曲线的斜率近似常数,约等于-2%初始弹性模量;4)平均压应力降低到屈服应力的20%后保持为常数.文献[7]建立如图 2所示屈曲钢筋的平均压应力应变关系,图中,拉应力应变曲线也代表不考虑屈曲时的压应力应变曲线,中间应变ε*由下式定义[7]:
|
| 图 2 屈曲钢筋压应力应变关系 Figure 2 Average compressive stress-strain for buckling bar |
式中:ε*/εy≥7.0;L/D为钢筋的长细比;fy的单位为MPa.根据ε*求得无屈曲时的应力σL*后,按照下式求得屈曲时对应的应力σ*[7].
式中:σ*≥0.2fy;α为参数,取值在0.75~1.0之间,文献[7]建议对于线性硬化的取1.0,而理想弹塑性的取0.75.
从图 2可以看出,屈曲钢筋压应力应变曲线分成4段:1)当应变不超过屈服应变时,曲线与无屈曲时相同;2)从屈服应变到中间应变ε*,曲线由下面的公式确定;3)中间应变ε*后应力应变为直线关系,斜率为初始弹性模量的-2%;4)当应力下降到0.2倍屈服应力后,其后应力保持为常数.
式中,σL为不考虑屈曲时(即拉应力应变关系)的应力.
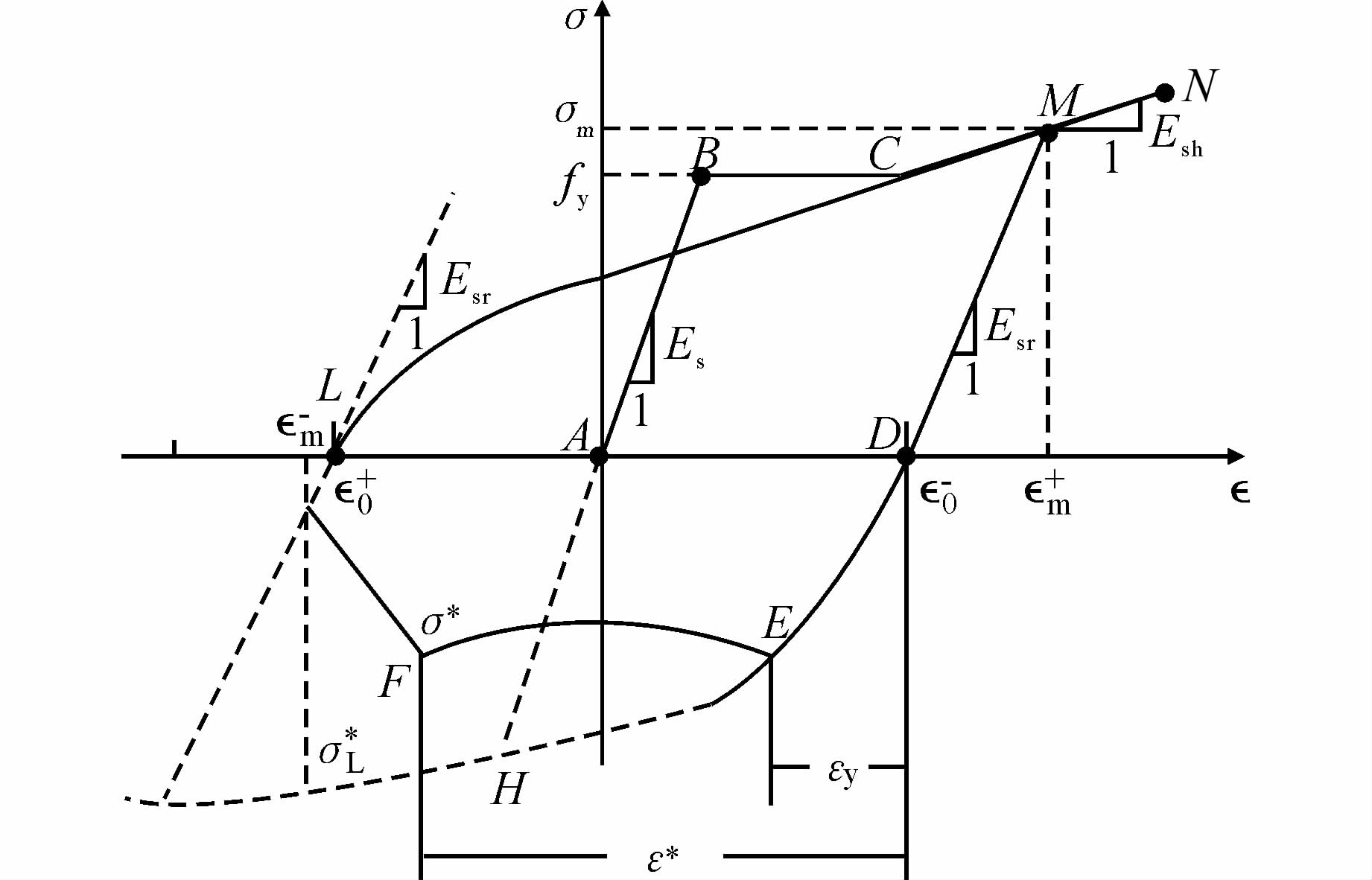
3 本文钢筋模型本文将Vecchio的单调荷载三折线应力应变曲线改为二折线,即钢筋屈服后进入硬化阶段,如图 3中ABC所示.第一次拉循环时,当拉应力超过屈服应力到达最大拉应变εm+对应的σm(图 3中M点)后,根据卸载刚度,应力直线下降至0(图 3中D点).继续反向加载,应力应变关系进入第一次压循环,当不考虑屈曲时,路径为图 3中DEHN曲线,第一次压循环取最大压应变为屈服应变,$\varepsilon _{m}^{-}=-{{\varepsilon }_{y}}$(即H点,DEH曲线由式(1)确定).当考虑屈曲时,路径为图 3中DEFG曲线,其中DE段与不考虑屈曲时路径一致,EF段的应力由式(6)计算,FG段为直线,其斜率为-0.02Es.第一次压循环结束后,卸载路径为GL,LM为第二次拉循环路径,而第二次压循环的最大应变为图中N点对应的应变.余下的循环依次进行.
|
| 图 3 本文钢筋滞回曲线 Figure 3 Present hysteresis stress-strain of bar |
本文利用ABAQUS的truss单元编写了钢筋材料的考虑屈曲和不考虑屈曲两种UMAT,不考虑屈曲的材料输入参数3个,即:Es(MPa)、fy(MPa)和Esh/Es(硬化刚度与初始刚度比值);而考虑屈曲的材料输入参数5个,除上述3个外,第4个参数为式(4)中的长细比L/D,第5个参数为式(5)中的α.
本文首先选择钢筋循环荷载的试验结果来验证本文方法的有效性.文献[5]以3组钢筋长细比分别为L/D=5、8和11(分别用A、B和C作为试件代号,钢筋直径也有3种,分别为16、20和24 mm)循环荷载试验结果为基础建立钢筋屈曲模型,文中给出了部分A和C组的试验结果,由于A组不存在屈曲效应,因此,本文选择C3作为验证对象.
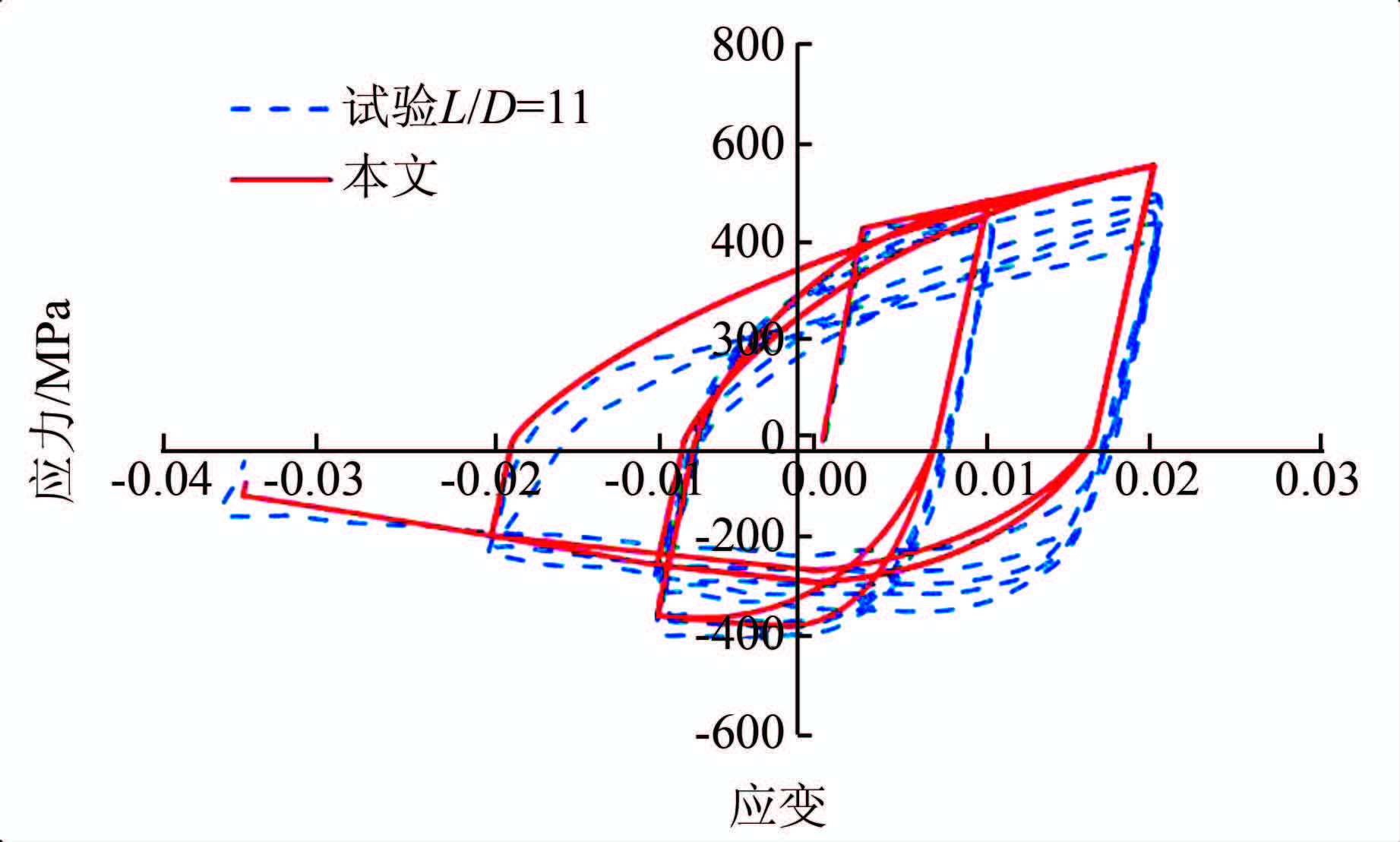
4.1 算例1:钢筋C3文献[5]中给出了C3试件的材料参数:Es=1.8×105 MPa,硬化刚度与初始刚度比为0.04,fy=430 MPa,L/D=11.本文用直径16 mm作为分析对象,钢筋长度为176 mm,用5个T2D2单元分析,α取1.图 4给出了单元3(中间单元)的应力应变滞回曲线分析结果与试验结果的对比.
|
| 图 4 C3试验与分析滞回曲线对比 Figure 4 Comparison of stress-strain responses for C3 |
从图 4可以看出,由于本文方法没有考虑钢筋的疲劳效应[8],所以同一变形条件的循环滞回曲线是重合的,而从试验结果中可以看出疲劳效应的存在,即同一变形的不同循环次数,钢筋的强度有所降低.除去疲劳效应外,本文的分析结果可以说很好地反映了钢筋屈曲所引起的强度降低,说明本文方法能有效地描述钢筋屈曲.
除钢筋循环荷载试验结果验证外,本文还选择了其中两个结构具有钢筋屈曲的3个钢筋混凝土结构作为算例,分别是文献[13]的钢筋混凝土梁R6、R2和文献[14]的剪力墙R1,涉及的钢筋长细比分别为4.7、5.6和10.7,以检验本文方法的有效性.在钢筋混凝土结构算例中,混凝土单元使用的是CSP4,混凝土材料使用的是MCFT模型[15].
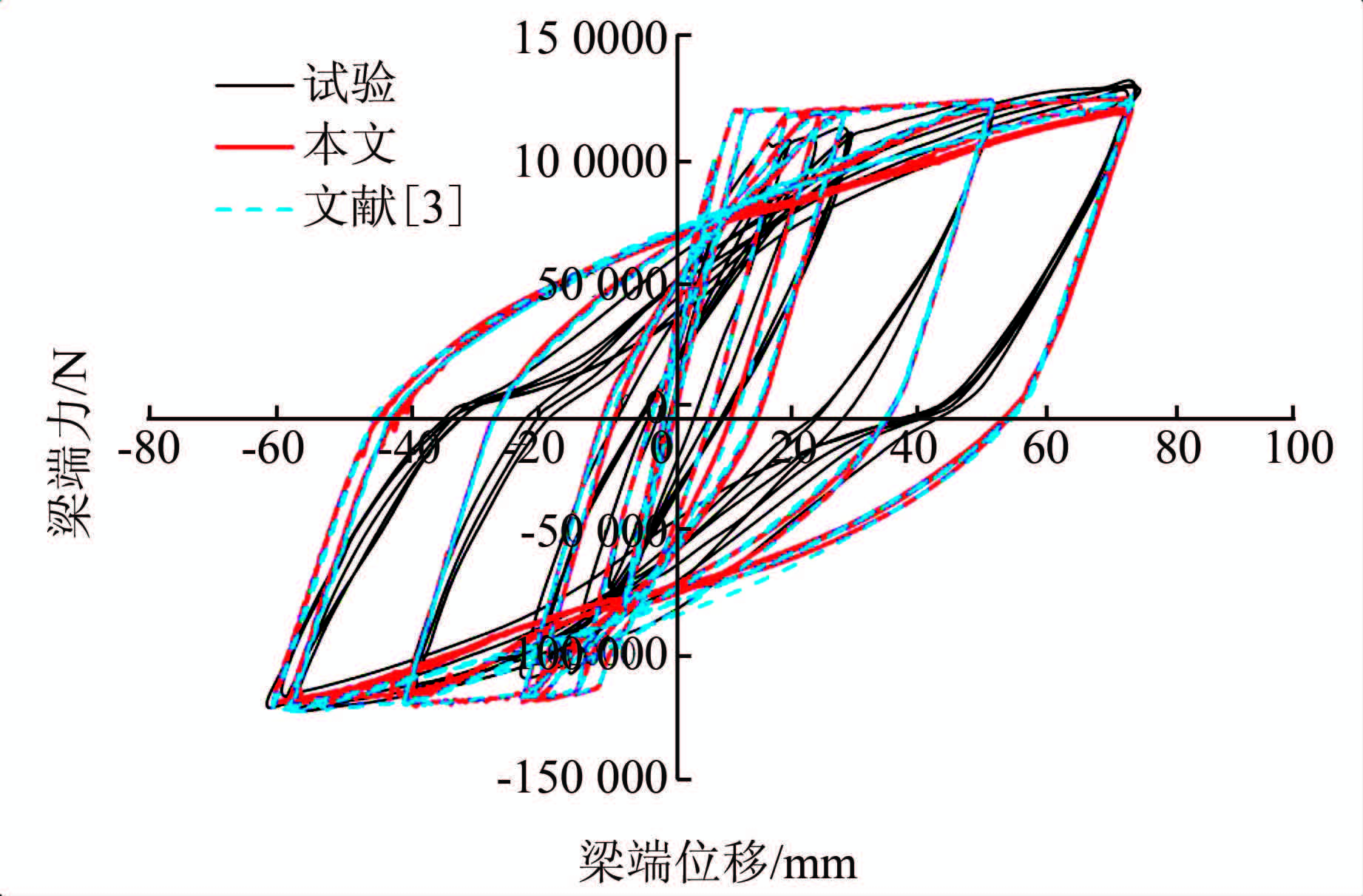
4.2 算例2:梁R6梁的截面尺寸为229 mm×406 mm,悬臂长度为1 600 mm.上下均配有4根直径为19.05 mm的纵筋(451 MPa)和间距为89 mm、直径为6.35 mm的四肢箍筋(413.8 MPa),混凝土圆柱体抗压强度为30 MPa,单元网格为8×18.钢筋的长细比为4.7,弹性模量取2×105 MPa,α取0.75.荷载位移滞回曲线的本文方法分析结果、Vecchio方法分析结果和试验结果对比见图 5.
|
| 图 5 R6试验与分析滞回曲线对比 Figure 5 Comparison of load-deflection responses for R6 |
从图 5可以看出,除刚度和强度有轻微下降外,考虑和不考虑屈曲影响对计算结果影响不大,这是因为本例的钢筋长细比为4.7,而影响屈曲的关键因素为长细比.当钢筋长细比小于5时,可以不计屈曲影响[5].虽然文献[7]认为这个结论对于高强钢筋来说是不妥的,这也说明对于普通钢筋来说文献[7]也是同意这个结论的.而本例中的钢筋为普通强度,本文的计算结果符合文献[5]结论.
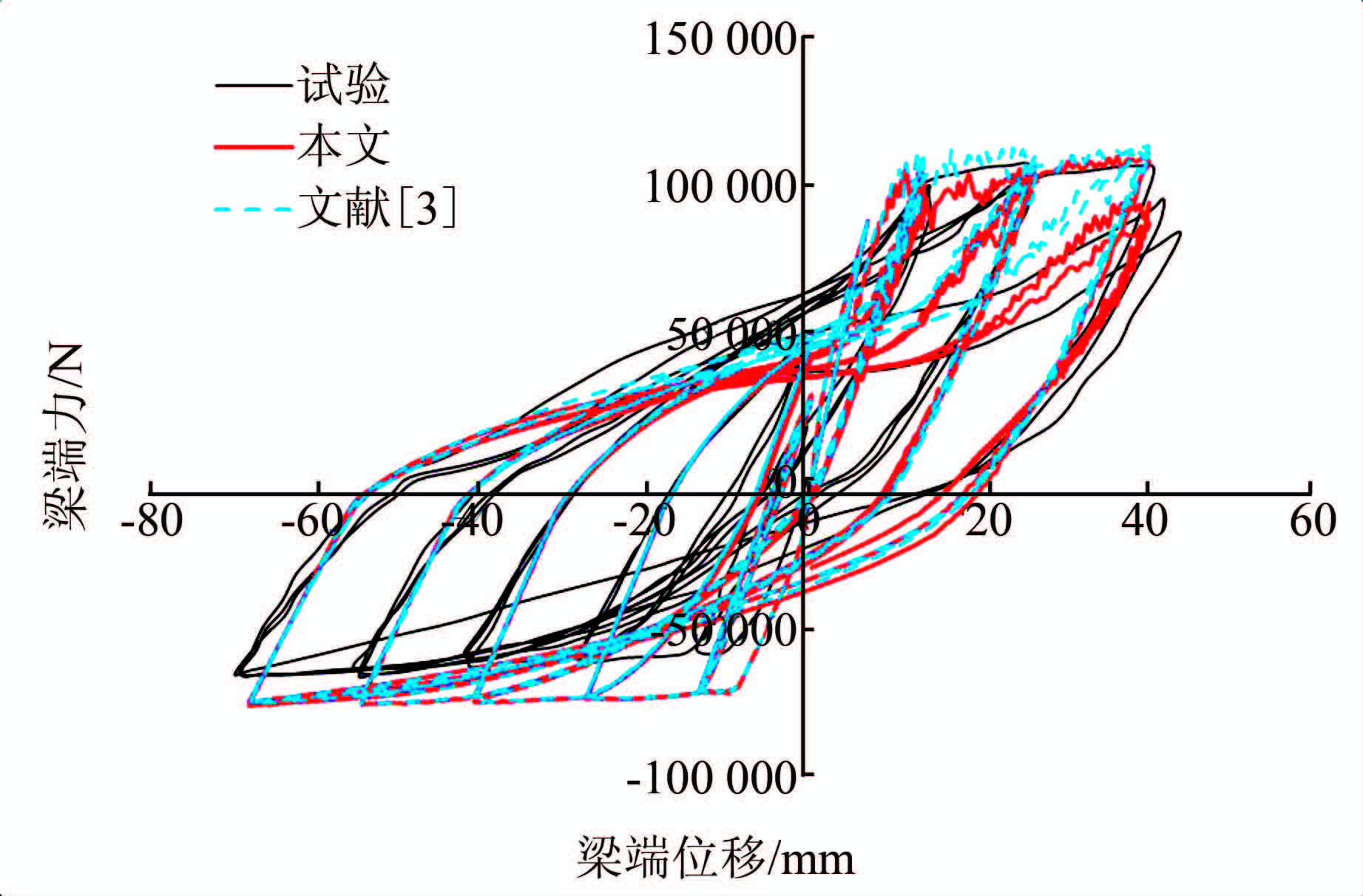
4.3 算例3:梁R2本例与算例2中的梁在几何尺寸上是完全相同的,梁上部钢筋与箍筋也同R6一样,仅底部改为3根直径16 mm的钢筋(458 MPa),混凝土棱柱体抗压强度29 MPa.其他数据同算例2,底部钢筋的长细比为5.6.荷载位移滞回曲线的本文方法分析结果、Vecchio方法分析结果和试验结果对比见图 6.
|
| 图 6 R2试验与分析滞回曲线对比 Figure 6 Comparison of load-deflection responses for R2 |
从图 6可以看出,试验结果在最后两次循环时,由于梁底部钢筋出现压屈后导致梁的刚度和强度降低,本文方法都能准确地描述,而不考虑钢筋屈曲的模型则不能描述试验中刚度和强度的突降现象,说明本文方法能有效描述钢筋屈曲效果.
4.4 算例4:剪力墙R1墙截面尺寸为101.6 mm×1 905 mm×4 572 mm.墙两边各配有4根直径9.5 mm纵筋(512 MPa)和直径5 mm间距101.6 mm的双肢箍筋(455 MPa),中间配有14根直径6 mm的纵筋(522 MPa)和间距203.2 mm的同样型号水平钢筋.混凝土圆柱体强度45 MPa,单元网格为10×23.墙体的主要弯曲钢筋的长细比为10.7,弹性模量取2×105 MPa,α取1.0.利用本文方法分析的荷载位移滞回曲线结果、利用Vecchio方法分析结果和试验结果对比见图 7.

|
| 图 7 R1试验与分析滞回曲线对比 Figure 7 Comparison of load-deflection responses for R1 |
当正向加载至76.2 mm的第二次循环时,剪力墙R1墙体最外边的钢筋出现屈曲,图 7试验曲线中强度和刚度突然下降是由屈曲钢筋被拉断引起的.由图 7可以看出,考虑钢筋屈曲的分析结果比不考虑钢筋屈曲的分析结果更加捏拢.由于受压钢筋屈曲导致墙体刚度降低,因此考虑受压钢筋屈曲的计算结果更符合试验结果,说明本文考虑钢筋屈曲计算方法是十分有效的.
从图 6和图 7可以看出,如果结构因钢筋屈曲而导致刚度或强度降低的现象,不考虑屈曲效应的钢筋模型是无法描述的,而本文建立的考虑屈曲效应的钢筋滞回模型则基本能够准确描述.
5 结论本文将文献[3]基于Ramberg-Osgood公式的循环荷载作用下的钢筋模型中拉压应力应变包络曲线的三折线简化为二折线后,再植入文献[7]考虑钢筋受压屈曲效应计算方法,成功地建立了考虑屈曲的循环荷载钢筋分析模型,并通过编制材料的UMAT程序将其移植到ABAQUS通用分析平台上,通过对1个钢筋和3个混凝土结构在循环荷载作用下的算例分析,验证了本文方法的有效性,可得出以下结论:
1) 本文建立的模型以及在ABAQUS通用软件上的二次开发,使得工程设计人员可以方便使用该程序在工程设计中考虑钢筋屈曲对工程设计的影响.
2) 本文所建立模型的有效性,也验证了钢筋长细比是影响钢筋屈曲仅有的影响因素,该结论是目前国际学术界的通识.
3) 本文分析结果验证了用钢筋平均压应力来描述屈曲钢筋的应力是有效的.
4)本文通过3种长细比钢筋混凝土结构的分析结果验证了以下结论:对于普通强度的钢筋,长细比L/D=5是钢筋是否屈曲的分界点,其对结构设计具有重要现实意义.
| [1] | Mengotto M, Pinto P E. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending [C] // Proceedings of the Conference on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, IABSE Reports Vol.13, Lisbon, 1973: 15-22. |
| [2] | Dodd L, Restrepo-Posada J I. Model for predicting cyclic behavior of reinforcing steel[J]. Journal of Structure Engineering, ASCE, 1995, 121(3): 433–445. DOI:10.1061/(ASCE)0733-9445(1995)121:3(433) |
| [3] | Vecchio F J. Towards cyclic load modeling of reinforced concrete[J]. ACI Structural Journal, 1999, 96(2): 192–202. |
| [4] | Filippou F C, Popov E P, Bertero V V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints [R]. University of California, Berkeley, 1983. |
| [5] | Monti G, Nuti C. Nonlinear cyclic behavior of reinforcing bars including buckling[J]. Journal of Structural Engineering, ASCE, 1992, 118(12): 3268–3284. DOI:10.1061/(ASCE)0733-9445(1992)118:12(3268) |
| [6] | Gomes A, Appleton J. Nonlinear cyclic stress strain relationship of reinforcing bars including buckling[J]. Engineering Structures, 1997, 19(10): 822–826. DOI:10.1016/S0141-0296(97)00166-1 |
| [7] | Dhakal R, Maekawa K. Modelling for post yielding buckling of reinforcement[J]. Journal of Structural Engineering, ASCE, 2002, 128(9): 1139–1147. DOI:10.1061/(ASCE)0733-9445(2002)128:9(1139) |
| [8] | Kunnath S K, Heo Y A, Mohle J F. Nonlinear uniaxial material model for reinforcing steel bars[J]. Journal of Structure Engineering, ASCE, 2009, 135(4): 335–343. DOI:10.1061/(ASCE)0733-9445(2009)135:4(335) |
| [9] | Korentz J. The effect of yield strength on inelastic buckling of reinforcing bars[J]. Mechanics and Mechanical Engineering, 2010, 14(2): 247–255. |
| [10] | Clough R W. Effect of stiffness degradation on earthquake ductility requirements [R]. University of California, Berkeley, 1966. |
| [11] | Qu Z, Ye L P. Strength deterioration model based on effective hysteretic energy dissipation for RC members under cyclic loading [C] // Proc.7th Intl. Conf. on Urban Earthquake Eng. & 5th Intl. Conf. on Earthquake Eng., 2010: 851-856. |
| [12] | Seckin M. Hysteretic behavior of cast-in-place exterior beam colum-slab subassemblies [D]. University of Toronto, 1981. |
| [13] | Ma S M, Bertero V V, Popov E P. Experimental and analytical studies on the hysteretic behavior of reinforced concrete rectangular and T-beams [R]. University of California, Berkeley, 1976. |
| [14] | Osterle R G, Fiorato A E, Johal L S, et al. Earthquake resistant structural walls-tests of isolated walls[J]. Construction Technology Laboratories, Portland Cement Association, Illinois, 1976. |
| [15] |
方自虎, 谢强, 周尧, 等. 循环荷载下MCFT混凝土结构模型[J].
地震工程与工程振动, 2015, 35(3): 1–6.
Fang Zihu, Xie Qiang, Zhou Yao, et al. MCFT model of concrete structures subjected to cyclic loading[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(3): 1–6. |
 2016, Vol. 49
2016, Vol. 49