文章信息
- 林建兵, 陈智雄, 姚国祥
- LIN Jianbing, CHEN Zhixiong, YAO Guoxiang
- 一种基于域密度的蚁群系统(AS)改进算法及结果解析
- An improved AS algorithm and result analyzing based on domain and its density
- 武汉大学学报(工学版), 2016, 49(4): 627-634
- Engineering Journal of Wuhan University, 2016, 49(4): 627-634
- http://dx.doi.org/10.14188/j.1671-8844.2016-04-024
-
文章历史
- 收稿日期: 2015-10-11
2. 莆田学院数学学院,福建 莆田 351100;
3. 莆阳网络系统公司,福建 莆田 351100
2. College of Mathematics, Putian University, Putian 351100, China;
3. Puyang Network System Corporation, Putian 351100, China
蚁群系统(Ant System) 于20世纪90年代初由意大利学者Macro Dorigo提出,作为一种经典的元启发式算法,AS受自然界的蚂蚁的觅食行为启发而提出用来在计算机上求解问题,因为其出色的性能而在TSP等组合优化问题上得到广泛的应用[1].后来的学者在最初的AS算法基础上,针对算法的相关参数进行了改进,相继提出了精华蚂蚁系统(Elitist Strategy for Ant System,EAS),基于排列的蚂蚁系统(AS rank,RAS),最大最小蚂蚁系统(MAX-MIN Ant System,MMAS)和蚁群系统(Ant Colony System,ACS)等[2-5],这些算法统称为ACO算法并逐渐形成了一系列比较成熟的算法框架,在路由、分配、子集、调度和机器学习等多种问题上显示出重要的应用价值.近年来,Rivero等人利用进一步改进的ACO算法来进行社交网络的路径搜索,取得了一系列的新成果[6];Jayadeva等人提出了一种改进的ACO算法EigenAnt并用数学方法证明了在可选择的信息素作用下最小路径是该算法的唯一均衡解[7];Dhananjay以及Munoz-Organero等分别在路径规划和资源过滤等方面取得了一些新的研究成果[8, 9].国内的一些学者也对蚁群优化算法进行了理论和应用研究,宋超等人利用ACO算法对传感器网络的节点自适应分布进行探索并取得了满意的解结果[10];黄翰等人基于吸收态Markov过程的数学模型,对蚁群算法本身的收敛速度进行深入分析,得出了利用此算法进行设计的一些指导原则[11];田志波等人构造了合成邻域以改进ACO算法性能并应用于板坯生产过程中,取得了不错的效果[12];夏亚梅等人提出了一种多信息素动态更新的蚁群算法并应用于Web服务组合的优化[13].随着对ACO算法内部作用机理了解的不断深入以及相关软硬件技术的发展,ACO及在此基础上进行改进的相关算法的应用范围不断扩大.
目前存在着大量的ACO算法及相关应用的文献主要是根据ACO算法自身存在的一些缺陷如收敛速度慢、容易陷入局部最优等情况而对算法内部的信息素或相关的参数进行修正所进行的探讨,如文献[3-5]等;或通过增加额外的调节参数或设置一些其他条件从而对问题的解的优化产生有利影响,如文献[7-9]和[11]等.文献[10、12]则研究了对某一具体问题利用ACO基本原理而进行问题求解的具体应用,存在着约束条件多、结论难以推广的问题.文献[6]考虑到了对应问题集的图中节点密集情况的问题,但是没有对节点的分布情况进行相应的处理.作为一种自组织的元启发性算法,蚁群优化算法对众多的类似组合优化的NP难问题是有效的解决工具之一,然而目前存在的文献却很少针对问题的节点分布的特征进行研究,以及研究节点的不同分布特征对解结果的影响.在现实情况中,人类社会和自然界的很多现象都表现出簇状分布的特征,如城镇的分布、昆虫的聚居情况、海洋众多鱼群的聚集以及网络节点的分布等.而在求解优化问题中,很多问题的节点分布情况将对解结果产生重要的影响,如同样节点个数的TSP问题,节点分布密集的收敛结果要比节点稀疏分布的收敛结果要小很多.在一个图中,有些地方的节点分布较密集,另外一些地方节点分布较稀疏,这种情况也将对ACO构建解的结果产生重要影响.通过分析几种经典ACO算法的具体求解过程可知:在处理TSP问题时,对节点数据进行初始化处理所需的时间和算法复杂度远远小于相对于路径寻优过程[2, 4, 5].为此下文将从ACO算法求解TSP问题的目标出发,对图中节点的分布特征进行分析研究,提出域和密度的概念,在此基础上构建DDACO(Domain Density ACO)蚁群优化算法,以处理类似TSP问题时节点分布具有显著差别的情况,并分别利用DDACO和AS算法对相应的仿真数据进行测试并作比较分析.
1 域和密度蚁群算法所涉及的问题大都可以归结为图的问题.为研究问题的方便,下文算法研究的图为无向对称图.对ACO问题所涉及图的节点分布情况进行研究,节点分布有2种情况:1)节点的分布有规律;2)节点分布杂乱,没有规律.如果节点分布有规律,比如按照等间距分布,那么问题最终可以转换成利用多项式来进行求解的过程;反之,问题就是一个NP难问题.下面引入域和密度概念,针对节点分布没有规律的情况进行问题的优化求解.
定义1:域是指平面的一个正方形区域,用符号SD来表示.一个域可以通过式子SDi:[O(x,y),r]来说明,其中O为域的原点,r为域半径(正方形的半径r为边长的1/2),(x,y)为原点对应的坐标,i=1,2,…,n.
定义2:密度是用来描述域节点分布密集情况的指标,用符号ρ来表示密度,任一域SDi的密度ρi可以通过式子ρi=Ni/Ai来表示,其中Ni为域SDi的节点数量,Ai为域SDi的面积.为计算方便,通常需要对Ai进行进一步的处理,通常让Ai=sqrt(Ai),sqrt为平方根函数.
按照上述定义,取图中某一点当做域的原点,对不同的域半径,域面积不同,其所包含的节点数将不同.对有限的节点,可以找到一个合适的原点和半径,成为最大域SDmax,将图中所有的节点都包含在最大域里.
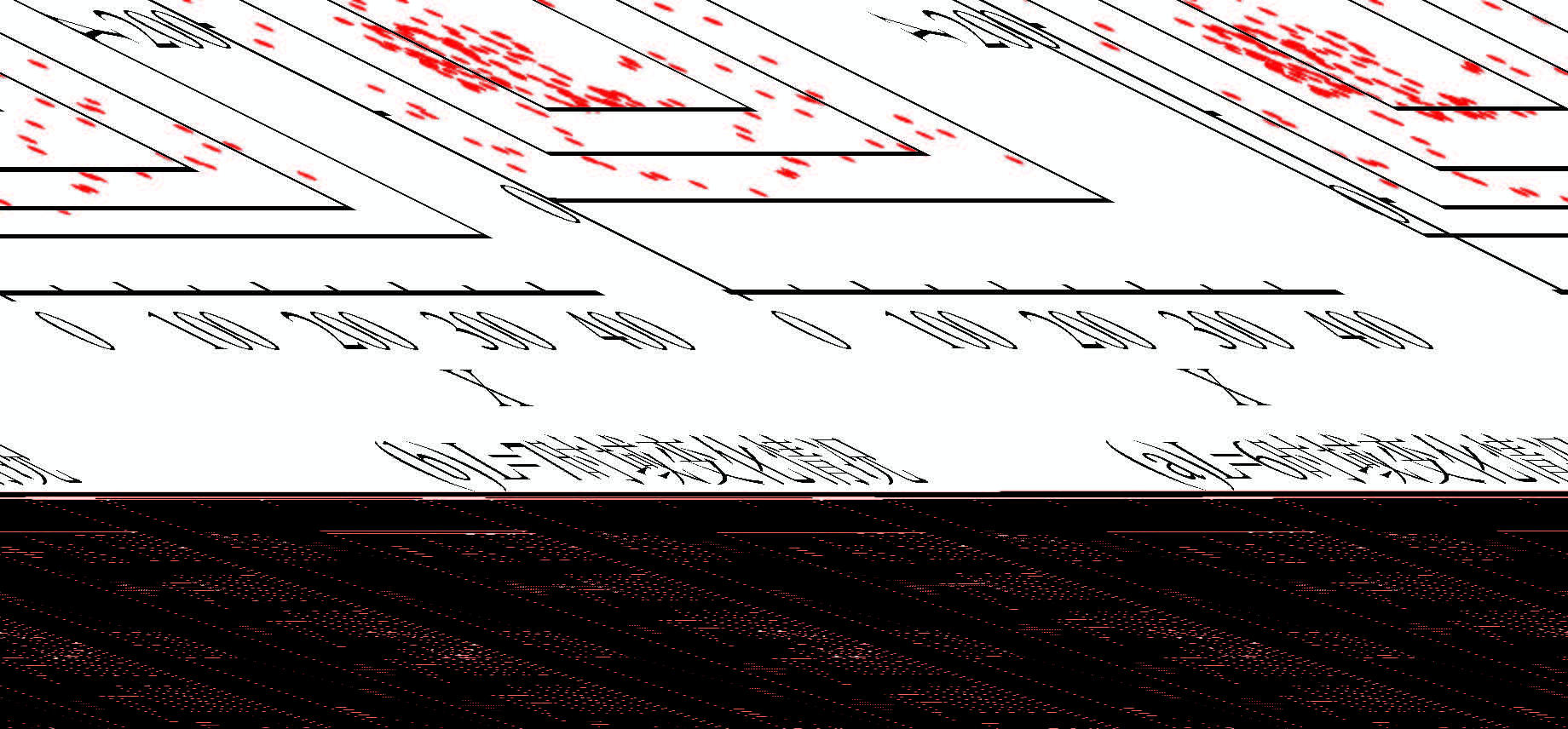
图 1所示是分别包含100、200个节点图的节点情况分布图(为方便起见,坐标轴单位为整数单位).假设图 1(a)和图 1(b)的域的半径都为100,可以根据各节点坐标算出各图的域包含的节点个数,假设图 1(a)中的域包含19个节点,图 1(b)中的域包含129个节点,根据上述定义,通过计算可得图 1(a)域密度ρ1=0.095,图 1(b)域密度ρ2=0.645,ρ2>ρ1.从图中也可以看出,图 1(b)的域中节点比图 1(a)的密集,这是由于对应域的密度比较大.在节点分布没有规律的情况下,通过密度,可以刻画出同等域下节点分布情况的一些特征.
|
| 图 1 不同节点分布及域 Figure 1 Different distributions of nodes and their domain |
DDACO算法求解TSP问题的主要目标是对于给定的图,寻找最优或较优路径,该路径遍历图中的所有节点.节点在图中的分布情况即设定的域和相应的密度对DDACO解的构建过程和最终结果具有重要影响,算法需要对此影响进行相应处理,为此作如下定义.
定义3:一个完全的DDACO问题的带权无向图用G=(V,E)来表示,其中V={v1,v2,…,vn}是带有n=|V|个节点的集合,E是完全连接这些点的边的集合.每一条边带有一条权值d(i,j)代表节点i和节点j之间的距离.
DDACO算法的目标就是要求找到图G中的1条最短回路,这条回路可以遍历图G中的每一个点1次且仅1次.即找到图G中所有点的所有排列π中一个权重之和最小的排列,目标函数为
在经典ACO算法中,随着图中节点数量的增加,问题的计算量急剧增加,相应的算法性能降低.针对节点的规模和性质,DDACO通过设定不同大小、数量的域来描述节点分布的特征.按照上一节的定义,域SD的形状为正方形,那么域的大小通过半径r来标识,显然r为边长的1/2,域的中心点即原点由域原点坐标O(x,y)来标识,当r=0时,规定域SD为一个点,r=+∞时,域为整个平面.
显然,如果r比较小,那么对应域包含的节点数量较少,寻找最优的f(π)容易实现,随着r的不断增加,寻找对应域的最优f(π)将越来越困难.根据文献[2, 4, 5]等大量的蚁群相关算法的研究得知,人工蚂蚁在寻找最优解的过程中容易陷入局部最优,因此寻找一个解在所有的域上都是最优解几乎是不可能的,可能的做法往往是寻找次优解并通过多次的循环过程从而逼近全局的最优解和一个较优解.对于图 1(b)所示的情况,所划定的域内密度显然明显高于图 1(a)的情况,人工蚂蚁若访问图 1(b)域内的某一点,则只有在域内其他所有距离较近的点都继续访问完再访问域外的点,这样才不会导致更长的路径,从而有可能得到全局的最优解或较优解.
按照上述的说明,从节点集在图中的分布情况入手,通过域和密度来确定人工蚂蚁的初始化动作及路径寻优过程的一些相应措施,从而构建ACO的改进算法DDACO.
2.2 具体构建 2.2.1 域的构建设图G中对应节点集为V = {v1,v2,…,vn},对于每一节点vi(i=1,2,…,n),对应的位置由vi(xi,yi)来表示,xi,yi分别对应平面上的横坐标和纵坐标.令xmax=max(x1,…,xn),xmin=min(x1,…,xn),max()表示取x1,…,xn中的最大值,min()表示取x1,…,xn中的最小值,同理,令ymax=max(y1,…,yn),令ymin=min(y1,…,yn),则最大域可以表示为
其中rmax=(xmax-xmin)/2, 或rmax=(ymax-ymin)/2.
可以算出对应最大域的密度为ρmax=n/sqrt(4rmax2)=n/2 rmax.
针对图G的规模,选择一整数作为域系数记为L,令Δr=(xmax-xmin)/L,Δr表示域半径的增量,最小域半径rmin=Δr.如果L为偶数,则域的数量为L/2;如果L为奇数,令域的数量为int(L/2)+1,其中的int表示取整数函数.对于图 2的节点分布,若选取L=6,域的数量为3,那么域的变化如图 2(a)所示;如L=7,域的数量为4,域的变化如图 2(b)所示.

|
| 图 2 域系数不同时时域变化情况 Figure 2 Variation of domain with different coefficients |
按照定义2,域的密度可以通过表达式ρi=Ni/sqrt(Ai)求得,必须计算各个域对应的节点数量.
假定L'为域的数量,当L为偶数时L'=L/2;当L为奇数时,L'=int(L/2)+1.域按照从小到大依次命名为SD1,SD2,…,SDmax,依据式(2)域的原点可以表示为 O(xmin+rmax,ymin+rmax),为下文方便表示,域原点坐标简单表示为:O(x,y).
按上述规定,最小域即SD1其半径rmin=Δr=(xmax-xmin)/2L',SDi域的半径为
ri=i·Δr ,i∈[1,L']
最小域面积:
Amin=4rmin2
任一vi(xi,yi)节点是否属于某一域用BEi来表示:
其中j∈[1,L'].
最小域节点数Nmin:
最小域密度ρmin:
所有域的密度求解式为
式中:ρj为第j个域的域密度.
2.2.3 优先域的选定通过2.2.1 节的说明可以知道,不同的域系数L将决定图的域的数量和大小.对于图中存在的各个域,DDACO算法需要确定一个域作为优先域.优先域里的节点聚集程度比较高,通常域的密度比较大,在DDACO算法蚂蚁信息素在优先域的释放可以根据需要进行调整,而且如果蚂蚁当前所在的节点位于优先域,那么在下一节点的选取过程中,优先域内的其他节点被选中的概率相应较大.可以按照如下的策略来进行优先域选取.
1) 密度最大优先策略:计算各个域对应的密度,选择最大密度的域作为优先域.如果最大密度的域不是最小域,则忽略比最大密度面积小的域.
2) 密集节点包含策略:选取的域能够最大程度包含密集节点,根据域半径的增量依次进行不同域的大小变化,直到包含所有的密集节点.
2.2.4 蚂蚁的行为DDACO中蚂蚁的行为参照文献[2]中基本ACO算法的做法,即图G中人工蚂蚁随机选择某一节点作为始发点,假设始发点为节点i,那么蚂蚁k选择j作为下一节点的概率:
其中:ηij=1/dij,表示预先给定的启发式信息,dij表示节点i和节点j之间的距离.
蚂蚁在行进过程中会释放信息素,τij表示节点i和节点j之间的信息素,信息素的更新为
其中λ为信息素挥发系数,0<λ<1.Δτij规定:
式中:C为一常量,可以取按照某一算法求出的路径长度.蚂蚁遍历完图中的所有节点之后,将回到始发点,这样蚂蚁就完成了一次的路径寻优过程.
2.3 仿真测试及结果分析根据域和密度的定义,结合DDACO算法策略的具体构建过程,对TSP问题进行DDACO实验仿真和结果分析,同时进行ACO算法中的AS仿真测试,并进行比较分析,所有的仿真都是在1台具有2G RAM系统时钟为2.50GHz的Intel Core 2双核个人PC上进行的.本节首先对DDACO算法的具体构建过程作实例化的描述,并解释一些关键的指标及其运算过程,然后对不同指标出现的不同结果进行分析和比较.大体上,DDACO算法具体构建过程可以分成下面的2个阶段,分别为初始化阶段和路径寻优阶段.
2.3.1 初始化阶段在初始化阶段,首先根据问题的规模,将节点的坐标分布情况利用相应的软件在平面图上大体生成节点的基本分布图.根据节点的分布图,确定域系数L,通常情况下,L的选取应让优先域有较大的密度,也就是让优先域包含尽量多的密集点,L的最终选择由密度的实验结果决定.表 1是一个具有50个节点的图的对应坐标数据(单位为整数单位).假设选取域系数L=4,那么域数量为int(4/2)=2,即域的数量L'为2.一旦确定完域的数量,接下来就要开始寻找优先域.首先必须确定域的原点位置和半径,由式(2)可以求得域的原点坐标和半径.首先求得最小横坐标xmin =1,最大横坐标xmax=197,最小纵坐标ymin=4,最大纵坐标ymax=98,那么最小域即SD1其半径rmin=Δr=(xmax-xmin)/2L'=49.域的原点坐标O((xmin+xmax)/2,(ymin+ymax)/2)为O(99,51),最小域为SDmin[O(99,51),49],第2个域为SD2[O(99,51),98].根据式(3)、(4)计算各个域对应的节点数分别为Nmin=42,N2=50.于是根据式(6)可以求得各个域对应的密度ρmin=42/sqrt(Amin)=0.429,ρ2=0.255.采取密度最大优先策略确定SD1为优先域.
确定完优先域,下一步需要对从原始的节点数据文件中读进来的数据按照优先域产生的状况进行重新存放,以便后续步骤对数据的使用.首先,按照所确定的优先域,计算优先域所对应的节点数目及位置情况.按照上面的计算结果,优先域包含42个节点,第2个域包含50个节点.由于SD1为优先域,所以首先将优先域的点的坐标分别存入一新的坐标数组,初始域以外的点存入新的坐标数组的后部,这样将产生按照所确定的优先域的新的节点坐标数据,由此可以计算对应的距离矩阵[5, 14].
确定完优先域并计算完距离矩阵后,DDACO需要对节点之间的信息素进行初始化.位于不同域的节点之间信息素初始化策略不同,通常情况下优先域内节点之间分配较高的初始信息素,其余域节点之间的信息素的初始值按照经典的ACO的做法[2].优先域内节点间的信息素初值的选择根据密度值来进行,通常情况下是一个和该域密度正相关的函数,也需要根据实验仿真的结果数据进行调整,但初值一定高于优先域外的信息素的初值.初始化的最后阶段是随机放置蚂蚁,蚂蚁可以放置在问题集的任一节点,蚂蚁的数量根据问题集的规模而定,Dorigo等人在文献[1]详细给出了各种经典的ACO算法的蚂蚁的合理数量,下文仿真实验的相关参数数据参考文献[1]对应参数的设定并将在需要调整的地方作相应的说明.
| x | y |
| 53 | 26 |
| 28 | 71 |
| 1 | 68 |
| 21 | 23 |
| 27 | 62 |
| 78 | 14 |
| 97 | 51 |
| 105 | 45 |
| 120 | 45 |
| 116 | 64 |
| 74 | 32 |
| 65 | 51 |
| 108 | 57 |
| 130 | 24 |
| 67 | 48 |
| 79 | 13 |
| 119 | 14 |
| 110 | 20 |
| 82 | 36 |
| 70 | 22 |
| 128 | 43 |
| 86 | 31 |
| 131 | 49 |
| 95 | 48 |
| 89 | 55 |
| 133 | 19 |
| 73 | 4 |
| 100 | 23 |
| 114 | 20 |
| 96 | 18 |
| 132 | 55 |
| 90 | 53 |
| 125 | 55 |
| 80 | 41 |
| 104 | 69 |
| 121 | 7 |
| 122 | 8 |
| 127 | 24 |
| 75 | 65 |
| 103 | 53 |
| 118 | 21 |
| 93 | 56 |
| 123 | 47 |
| 71 | 22 |
| 72 | 59 |
| 142 | 98 |
| 157 | 70 |
| 170 | 66 |
| 185 | 29 |
| 197 | 90 |
DDACO在蚂蚁完成初始化阶段后,进入路径寻优阶段.这一阶段,每只蚂蚁从所有的节点中随机选取一节点作为出发点,然后根据该出发点到可选节点的各条路径上的信息素的情况根据式(7)进行概率计算,并按照轮盘赌的方式概率选择下一节点,在行进到下一节点的过程中,释放一定量的信息素,为了和AS算法进行比较,信息素的释放规则和AS系统相同[2].在此过程中,蚂蚁将会判断出发点是否位于优先域内,如果出发点位于优先域内,那么蚂蚁将对可选节点是否也位于优先域内进行逐一判断.如果可选节点也位于优先域内,蚂蚁将对按照式(7)计算出来的概率增加一概率增量,以表示优先域内部的节点之间选择的可能性增加,如果出发节点和可选节点没有同时位于优先域内部,蚂蚁选择下一节点的概率仍然按照式(7)计算.蚂蚁将重复上述的动作,直到图中所有的节点都选择完毕,这样蚂蚁就完成了1次循环.之后蚂蚁将重新进行初始化,然后继续进行路径寻优,并将结果和上一次的寻优结果进行比较,将比较后较优的结果保存下来.循环的次数作为参数可以进行控制.
按照上述的过程针对表 1数据所示的具有50个节点的图TSP问题求解仿真,令DDACO算法中域系数为4,优先域内节点之间的信息素初值为0.3,其余的节点之间的信息素初值为0.1,蚂蚁数为50,α为1,β为3,ρ为0.7,循环次数为50时,图 3说明了对于不同给定的概率增量DDACO的运算仿真结果情况.

|
| 图 3 不同概率增量的DDACO仿真结果 Figure 3 Simulation results of DDACO with different probability increments |
在图 3中,RunTimes表示循环次数,BestLength表示最后收敛值.从图 3可以看出,针对几种不同的概率增量,DDACO都表现出收敛于一个较低值的情况,随着循环次数的增加,即使是在遭遇一个比较大的初值的情况下(如p=0.007的情况),DDACO也能和较低的概率增量一样收敛于一个较优值.进一步的仿真测试表明,概率增量对应此去0.007到0.01之间比较合适.然而,对同样的节点数据和相同的参数设定,利用AS算法进行仿真测试,结果表明DDACO算法无论是在时间或是在收敛值的情况下都不占据明显的优势.这可以通过分析DDACO和ACO算法的具体运行过程得到解释:对于表 1所示的数据,DDACO算法的优先域包含了42个节点,剩余节点在优先域外比较平均地分散分布,由于节点数、蚂蚁数和循环次数都比较少,几次循环过后各条路径上的信息素差异比较明显,导致DDACO算法和ACO算法的蚂蚁在优先域内具有相同的行为,因此仿真结果没有明显的区别.但是当循环次数增多时,进一步的仿真结果表明:得到同样的结果,DDACO所耗费的时间却远远小于AS系统耗费的时间.这是由于经过多次循环后,优先挥发系数的作用,各条路径上的信息素浓度下降,蚂蚁通过信息素进行路径的轮盘式概率选择的计算量增加,由于DDACO算法在计算时给优先域内的点额外的概率增量,从而减少了相关过程的计算量,使得整个运算过程的时间减少.根据Blum和Sampels等人研究相关AS算法性能的相关文献得知:随着图的节点、蚂蚁数量或循环次数的增加,ACO算法很可能陷入局部最优或搜索停滞的状态,相关性能指标急剧下降[15, 16].为此,下面继续通过增加节点数和调整相应的参数来测试DDACO在一些方面所具有的优势.
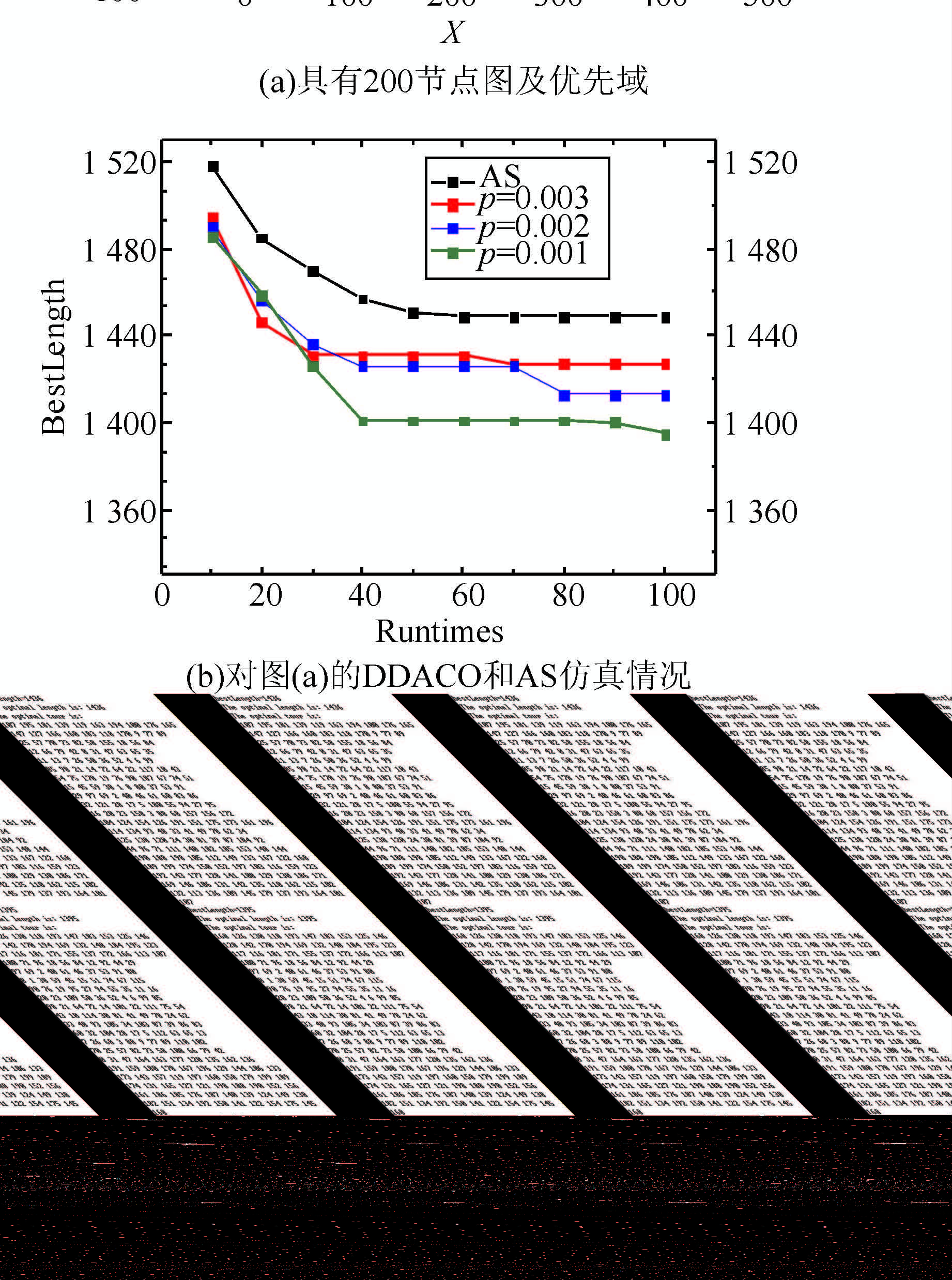
构造一个在局部区域节点比较密集的具有200个节点的图,图的节点分布情况如图 4中(a)所示(坐标轴单位为整数单位),选择DDACO算法中域系数为6,优先域D1如图 4(a)所示.优先域内节点之间的信息素初值为0.3,其余节点之间的信息素初值为0.1,蚂蚁数为200,α为1,β为3,ρ为0.7,循环次数为100时,图 4(b)给出了对于不同给定的概率增量DDACO和AS的运算仿真结果情况.
|
| 图 4 对200节点的图DDACO和AS仿真 Figure 4 Simulation results of DDACO and AS with 200 nodes |
从图 4(a)中可以看出,在X值的100~300以及Y值100~300之间具有一些比较密集的点,因此DDACO算法在优先域里囊括了这些密集点,并对这些点按照信息素分配的策略和概率处理策略进行了处理,然后根据不同的参数和AS系统进行测试,结果显示在图 4(b)中,图中显示,对应不同的几种概率增量,DDACO的收敛结果都优于AS,在时间上也有优势.通过增加循环次数的进一步测试表明,DDACO算法的性能随循环次数的增加相对于AS有大幅度的提高.为进一步分析DDACO算法性能得到提升的原因,图 5、6分别给出了利用AS算法和DDACO算法(p=0.001)情况下经过100次循环的最优结果和行走路径.从图 5、6可以看到,通过分析行走路径的差异,可以看到2种算法得到的结果不同.图 5中,蚂蚁在最后的搜索路径中所经过的节点在优先域内外没有什么规律地交错进行,而在图 6中,蚂蚁的最终搜索路径自当前选中节点落在优先域内部时,后续的一系列节点几乎都从优先域内部进行选择,这直接导致最终结果比较接近最优值.当当前节点位于优先域内部时,虽然AS系统中的蚂蚁通过信息素和路径启发信息也能够以较大概率从优先域内部进行,但是随着循环次数的增加挥发系数不断弱化信息素和路径启发信息的作用,结果是容易陷入局部最优和搜索停滞.
|
| 图 5 AS最优结果和行走路径 Figure 5 Optimal results and route of AS |
|
| 图 6 DDACO最优结果和行走路径 Figure 6 Optimal results and route of DDACO |
通过改变图中的节点数量、蚂蚁数量和循环次数,对DDACO和AS算法进行进一步的仿真测试,表 2列出了对几种样本数据进行10次仿真实验的平均收敛结果和平均耗费时间.
从表 2可以看出,当节点个数和蚂蚁数量为60时,AS和DDACO在循环次数为200次时在时间和最终收敛值上几乎没有什么差别,随着循环次数的增加,二者在收敛值方面都有改善,其中DDACO改善更为明显,同样在时间上DDACO也较有优势.当节点数和蚂蚁数量增加到200时,DDACO的收敛值和耗费时间较AS具有明显的优势,随着循环次数增加时,这种优势更加明显.当节点规模和蚂蚁数量增加到600时,AS和DDACO所需的时间都急剧增加,但是DDACO最终耗费的时间却不到AS的一半,收敛值也远远优于AS;并且还能观察到,尽管循环次数增加,然而AS系统的收敛值没有得到进一步的优化,DDACO在此时随着循环的继续增加,收敛值有继续向好的趋势.这是由于当循环次数增加到一定次数时,AS系统的各条边上的信息素几乎不起作用,寻优工作陷入停滞;而DDACO由于有额外的信息素和概率增量,从而使得寻优工作能够继续进行.
| 节点数 | 蚂蚁数 | 循环次数 | B.L. | R.T./s | ||
| AS | DDACO | AS | DDACO | |||
| 60 | 60 | 200 | 319 | 315 | 10.43 | 10.19 |
| 60 | 60 | 500 | 292 | 281 | 56.13 | 49.26 |
| 200 | 200 | 200 | 1 531 | 1 446 | 1 712 | 1 638 |
| 200 | 200 | 500 | 1 489 | 1 365 | 13 256 | 8 136 |
| 600 | 600 | 200 | 12 315 | 7 613 | 13 6231 | 61 236 |
| 600 | 600 | 500 | 12 363 | 7 012 | 468 125 | 15 683 |
研究了蚁群算法中的图的节点分布的一些特征,在此基础上提出了域和密度的概念,并对具有密集点特征的图构建DDACO算法.文中详细描述了DDACO算法策略以及具体的构建过程,利用仿真数据对DDACO算法进行了测试,并和AS算法的测试结果进行比较,结果表明DDACO在问题规模集比较大时且具有明显的密集点特征时较AS具有明显的时间和收敛性能上的优势.
未来将对DDACO如何应用于具有若干块随机分布的密集区域的图进行研究,并致力于寻找制约DDACO算法收敛速度和收敛值的深层次原因以及数据敏感性问题,使得DDACO算法的性能得到进一步的提升并且具有更大的适用范围.
| [1] | Dorigo M, Stutzle T. Ant Colony Optimization[M]. Cambridge, MA: The MIT Press, 2004: 26-46. |
| [2] | Dorigo M, Gambardella L M. Ant colonies for the traveling salesman problem[J]. BioSystems, 1997, 43(2): 73–82. DOI:10.1016/S0303-2647(97)01708-5 |
| [3] | Bullnheimer B, Hartl R F, Strauss C. A new rank based version of the ant system—A computational study[J]. Central European Journal for Operations Research and Economics, 1999, 7(1): 25–38. |
| [4] | Stutzle T, Hoos H. MAX-MIN ant system[J]. Future Generation Computer Systems, 2000, 16(8): 889–914. DOI:10.1016/S0167-739X(00)00043-1 |
| [5] | Dorigo M, Gambardella L M. Ant colony system: A cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53–66. DOI:10.1109/4235.585892 |
| [6] | Rivero J, Cuadra D, Calle J, et al. Using the ACO algorithm for path searches in social networks[J]. Applied Intelligence, 2012, 36(4): 899–917. DOI:10.1007/s10489-011-0304-1 |
| [7] | Jayadeva, Sameena Shah, Amit Bhaya, et al. Ants find the shortest path:a mathematical proof[J]. Swarm Intelligence, 2013(3): 43–62. |
| [8] | Dhananjay Thiruvady, Gaurav Singh, Andreas T, et al. Constraint-based ACO for a shared resource constrained scheduling problem[J]. International Journal of Production Economics, 2013, 141(1): 230–242. DOI:10.1016/j.ijpe.2012.06.012 |
| [9] | Munoz-Organero M, Ramirez G, Merino P, et al. Analyzing convergence in e-learning resource filtering based on ACO techniques: a case study with telecommunication engineering students[J]. IEEE Transactions on Education, 2010, 53(4): 542–546. DOI:10.1109/TE.2009.2032168 |
| [10] |
宋超, 刘明, 龚海刚, 等. 基于蚁群优化解决传感器网络中的能量洞问题[J].
软件学报, 2009, 10(20): 2729–2743.
Song Chao, Liu Ming, Gong Haigang, et al. ACO-based algorithm for solving energy hole problems in wireless sensor networks[J]. Journal of Software, 2009, 10(20): 2729–2743. |
| [11] |
黄翰, 郝志峰, 吴春国, 等. 蚁群算法的收敛速度分析[J].
计算机学报, 2007, 30(8): 1344–1356.
Huang Han, Hao Zhifeng, Wu Chunguo, et al. The convergence speed of ant colony optimization[J]. Chinese Journal of Computers, 2007, 30(8): 1344–1356. |
| [12] |
田志波, 唐立新, 任一鸣, 等. 基于合成邻域的蚁群算法求解无委托板坯匹配问题[J].
自动化学报, 2009, 35(2): 186–192.
Tian Zhibo, Tang Lixin, Ren Yiming, et al. Solving open-order Slab matching problem by ACO with compound neighborhood[J]. ACTA Automatic Sinica, 2009, 35(2): 186–192. DOI:10.3724/SP.J.1004.2009.00186 |
| [13] |
夏亚梅, 程渤, 陈俊亮, 等. 基于改进蚁群算法的服务组合优化[J].
计算机学报, 2012, 35(2): 270–281.
Xia Yamei, Cheng Bo, Chen Junliang, et al. Optimizing service composition based on improved ant colony algorithm[J]. Chinese Journal of Computers, 2012, 35(2): 270–281. DOI:10.3724/SP.J.1016.2012.00270 |
| [14] | Dorigo M. Optimization, learning and natural algorithm[D]. Milan:Dipartimento di Elettronica,Politecnico di Milano,1992. |
| [15] | Blum C, Sampels M. When model bias is stronger than selection pressure[C]//Proceedings of the Seventh International Conference on Parallel Problem Solving from Nature.Berlin:Springer-Verlag, 2002: 893-902. |
| [16] | Blum C, Sampels M, Zlochin M. On a particularity in model-based search[C]//Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2002). San Francisco:Morgan Kaufmann, 2002: 35-42. |
 2016, Vol. 49
2016, Vol. 49



