文章信息
- 王志杰, 何晟亚, 王国栋, 王宁, 何明磊
- WANG Zhijie, HE Shengya, WANG Guodong, WANG Ning, HE Minglei
- 轴对称解析解对马蹄形隧道衬砌水压力及渗透量适用性研究
- Study of applicability of an axisymmetric solution for water pressure and seepage flow on lining of horseshoe shaped tunnel
- 武汉大学学报(工学版), 2016, 49(1): 54-59
- Engineering Journal of Wuhan University, 2016, 49(1): 54-59
- http://dx.doi.org/10.14188/j.1671-8844.2016-01-009
-
文章历史
- 收稿日期: 2015-05-07
现在各个部门采用不同措施和计算方法[1-4]来计算公路、铁路、地铁、水工隧道的水荷载,并结合经验进行设计.近年来,大量隧道的施工都会遇到水荷载的作用,例如福建厦门翔安隧道、大连海底隧道和克色克阔兹隧道等等.不少研究学者发表了不少关于水荷载的论文,王建秀等在深埋隧道衬砌水荷载计算的基本理论中,对渗流场和外水压力作用系数进行了研究[5] ;李伟等以渗流连续性方程和Darcy定律为基本原理,总结围岩注浆加固圈、初期支护和排水系统对地下渗流的主要影响因素[6];李鹏飞等基于地下水水力学理论,推导海底隧道渗水量和符合衬砌结构外水压力的计算方法[7];郑波等在复合式衬砌等效渗透系数的基础上,利用整体式衬砌结构的水压力计算方法估算衬砌水压力[8];张民庆通过现场监测水压力值,分析水压力曲线特征,提出注浆后二次衬砌水压力设防建议[9];李苍松等在隧道地下水处置的设计理论及方法研究中,结合模型试验和理论计算,提出了防排水原则[10]等.
上述研究给予不同的理论基础,考虑的因素和关注的中心也各不相同,具有各自的优势和适用性.为丰富隧道衬砌水压力及内力分析方法,这里阐述一种在隧道断面为轴对称形状的情况下,基于隧道断面形状等效周长公式和轴对称解析解公式用于简化马蹄形断面计算隧道衬砌水压力荷载及渗透量的方法,并将其与同等条件下的FLAC3D有限差分法数值分析结果进行对比,验证其合理性和得到马蹄形隧道衬砌水压力荷载与内力规律.何明磊[11]等在圆形隧道亦采用该方法进行相关研究,本文亦是对该方法的拓展.
1 简化的轴对称解析解和等效周长公式假设围岩、衬砌和注浆加固圈为不同材料的均匀连续各向同性介质,并且满足Darcy渗流定律.设远水场的水头为H,求解圆形隧道的衬砌内表面渗透量和衬砌外水压力,轴对称解析计算见图 1.图中:k1为衬砌渗透系数,cm/s;kg为加固圈渗透系数,cm/s;kr为围岩渗透系数,cm/s;r0为衬砌内半径,m;r1为衬砌外半径,m;rg为加固圈半径,m;H为隧道中心水头,m.
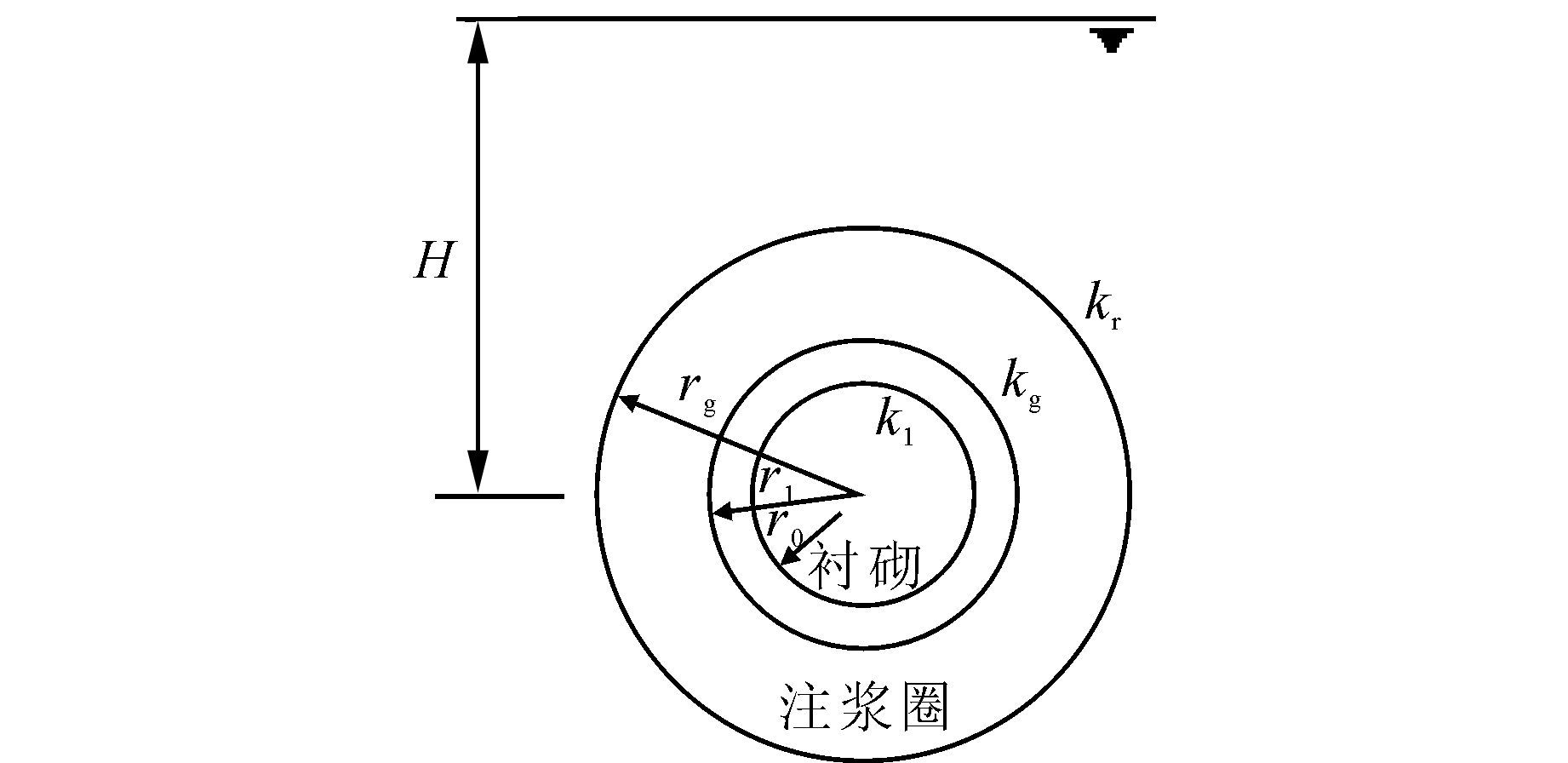
|
| 图 1 轴对称解析计算图示 Figure 1 The calculation of the axisymmetric analytic method |
通过计算可以求解得到衬砌内表面渗透量、衬砌背后水压力:
从式(1)、(2)可以看出:
1) 当衬砌不透水时,Q=0,p=γH;
2) 当衬砌的渗透系数增大时,Q增大,p减小;
3) 当注浆圈半径、衬砌半径提高时,Q、p影响趋势一致.
施作衬砌前渗透量为
水荷载折减系数为
式(4)可以作为实际工程中监测渗透量反分析水荷载折减系数.
以上为圆形隧道的轴对称解析解,而对于马蹄形隧道,则需要考虑等效半径[12].利用等效周长法,通过将马蹄形断面尺寸转化为圆形断面尺寸,即隧道内径、外径等效成圆形隧道的几何参数,等效尺寸见表 1,其公式为
| 衬砌厚度/m | 衬砌内周长/m | 等效衬砌内径/m | 衬砌外周长/m | 等效衬砌外径/m |
| 0.3 | 43.82 | 6.97 | 47.59 | 7.27 |
| 0.6 | 43.82 | 6.97 | 47.59 | 7.57 |
| 0.9 | 43.82 | 6.97 | 47.59 | 7.87 |
通过有限差分法数值软件计算和轴对称解析计算分别进行衬砌水压力、渗透量及衬砌内力计算,实际中衬砌背后盲管排水等效为衬砌渗透排水,分别比较3种工况:1)不同衬砌渗透系数下衬砌水压力、渗透量、衬砌内力及数值计算与轴对称解析解之间的误差;2)不同注浆半径下衬砌水压力、渗透量、衬砌内力及数值计算与轴对称解析解之间的误差;3)不同衬砌半径下衬砌水压力、渗透量、衬砌内力及数值计算与轴对称解析解之间的误差.计算中采用水工隧道提出的荷载折减系数βw概念:
式中:p为衬砌水压力,Pa;βw为水荷载折减系数;γ为水的重度,kN/m3;H为水头高度,m.
2.2 计算参数根据《铁路隧道设计规范》,选取Ⅳ级围岩和地下水物理力学参数作为计算参数,见表 2.
| Ⅳ围岩参数 | 水参数 | ||||||
| 重度/(kN·m-3) | 变形模量/GPa | 泊松比 | 内摩察角/(°) | 黏聚力/MPa | 密度/(kg·m-3) | 抗拉强度/MPa | 体积模量/MPa |
| 20 | 3 | 0.3 | 30 | 0.4 | 1 000 | 0 | 2×103 |
利用有限差分法软件FLAC3D建立渗流模型,见图 2.模型的高度为100 m,宽度为100 m,隧道中心在模型的中心,即隧道中心到模型的上下边界为50 m,至模型的左右边界均为50 m,沿隧道轴线方向取单位长度.隧道中心的水头高度为50 m,埋深为42.15 m,隧道区域的几何形状为马蹄形.力学模型的边界均受到法向的约束,渗流模型中开挖围岩界面或衬砌外表面的孔隙水压力取p=0.根据对称性,分析点2与分析点4的计算结果相同,所以仅记录分析点1、3的计算结果并进行比较分析,分析点编号见图 3.

|
| 图 2 FLAC3D渗流模型 Figure 2 Seepage model in FLAC3D |
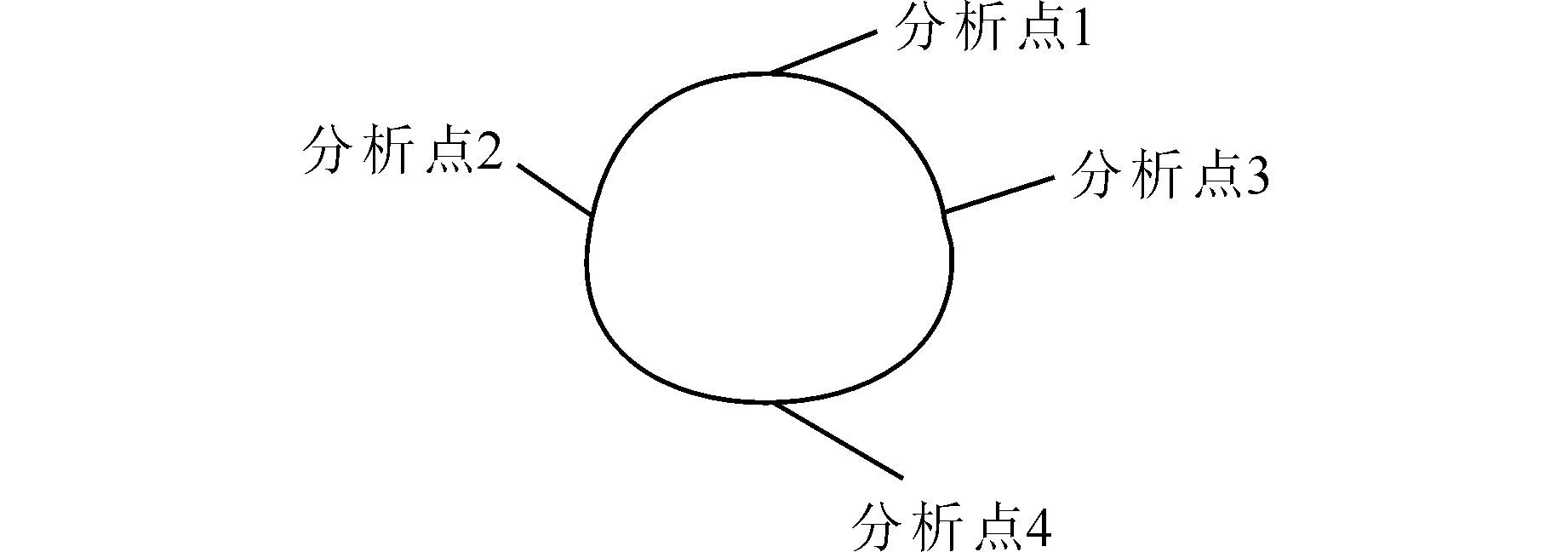
|
| 图 3 分析点编号示意图 Figure 3 The analytical point number |
不考虑固体介质压缩性的情况下,在不同工况下衬砌的透水性能各不相同,作用在衬砌上的水荷载也各不相同.通过分析不同工况下衬砌单元应力,考虑弹塑性理论,可以得到各个单元的弯矩与轴力,并根据《铁路隧道设计规范》(TB10003-2005),运用容许应力法计算安全系数.
3 结果分析对上述的3种工况进行分析,分别运用等效周长下的轴对称解析计算与有限差分法数值计算,可以得到相应情况下的分析点1、2、3的内力值以及渗透量情况,并根据《铁路隧道设计规范》(TB10003-2005)中的容许应力法计算安全系数.围岩渗透系数为1.0×10-3 cm/s、衬砌厚度为0.6 m时,不同衬砌渗透系数下衬砌水压力、渗透量及衬砌内力分别见表 3、4;围岩渗透系数为1.0×10-3 cm/s、注浆渗透系数为1.0×10-5 cm/s、衬砌厚度0.6 m时,不同注浆半径下衬砌水压力、渗透量及衬砌内力分别见表 5、6;围岩渗透系数为1.0×10-3 cm/s、衬砌渗透系数为1.0×10-5 cm/s、内表面净空不变时,不同衬砌厚度下衬砌水压力、渗透量及衬砌内力分别见表 7、8.
| 衬砌渗系数/(cm·s-1) | 水压力/Pa | 折减系数 | 渗透量/(m2·(s·m-1)-1) | ||||
| 分析点1 | 分析点2 | 分析点3 | 理论值 | 数值解 | 理论解 | ||
| 1.0×10-3 | 8.39×103 | 1.83×104 | 2.86×104 | 1.93×104 | 0.05 | 1.59×10-3 | 1.47×10-3 |
| 1.0×10-4 | 1.10×105 | 1.43×105 | 1.75×105 | 1.37×105 | 0.32 | 1.11×10-3 | 1.04×10-3 |
| 1.0×10-5 | 3.35×105 | 3.71×105 | 4.60×105 | 3.49×105 | 0.83 | 2.83×10-4 | 2.66×10-4 |
| 1.0×10-6 | 4.11×105 | 4.44×105 | 5.51×105 | 4.13×105 | 0.97 | 3.39×10-5 | 3.14×10-5 |
| 不透水 | 4.21×105 | 4.81×105 | 5.63×105 | 4.81×105 | 1.00 | 0 | 0 |
| 渗透系数/(cm·s-1) | 分析点1 | 分析点2 | 分析点3 | ||||||
| 弯矩/(kN·m) | 轴力/kN | 安全系数 | 弯矩/(kN·m) | 轴力/kN | 安全系数 | 弯矩/(kN·m) | 轴力/kN | 安全系数 | |
| 1.0×10-3 | -19.48 | -1 615 | 5.57 | 212.21 | -5 363 | 1.67 | -60.01 | -1 530 | 5.84 |
| 1.0×10-4 | -18.88 | -1 685 | 5.34 | 203.73 | -5 325 | 1.68 | -62.64 | -1 595 | 5.60 |
| 1.0×10-5 | -18.53 | -1 823 | 4.94 | 187.84 | -5 255 | 1.71 | -68.47 | -1 708 | 5.23 |
| 1.0×10-6 | -37.89 | -1 880 | 4.79 | 99.54 | -5 212 | 1.73 | -80.91 | -1 745 | 5.07 |
| 不透水 | 27.91 | -1 803 | 4.99 | 46.07 | -4 986 | 1.80 | 54.60 | -1 646 | 5.47 |
| 无水 | 23.93 | -1 482 | 6.07 | 39.06 | -4 170 | 2.16 | 46.27 | -1 344 | 6.69 |
| 注:轴力受压为正,弯矩内侧受拉为负. | |||||||||
| 注浆半径/m | 水压力/Pa | 折减系数 | 渗透量/(m2·(s·m-1)-1) | ||||
| 分析点1 | 分析点2 | 分析点3 | 理论值 | 数值解 | 理论解 | ||
| 0 | 3.35×105 | 3.73×105 | 4.60×105 | 3.49×105 | 0.83 | 2.84×10-4 | 2.66×10-4 |
| 1 | 3.02×105 | 3.32×105 | 4.12×105 | 3.14×105 | 0.74 | 2.53×10-4 | 2.39×10-4 |
| 2 | 2.77×105 | 3.03×105 | 3.77×105 | 2.88×105 | 0.68 | 2.30×10-4 | 2.19×10-4 |
| 3 | 2.58×105 | 2.81×105 | 3.49×105 | 2.68×105 | 0.64 | 2.14×10-4 | 2.04×10-4 |
| 注浆半径/m | 分析点1 | 分析点2 | 分析点3 | ||||||
| 弯矩/(kN·m) | 轴力/kN | 安全系数 | 弯矩/(kN·m) | 轴力/kN | 安全系数 | 弯矩/(kN·m) | 轴力/kN | 安全系数 | |
| 0 | -18.53 | -1 823 | 4.94 | 187.84 | -5 255 | 1.71 | -68.47 | -1 708 | 5.23 |
| 1 | -38.03 | -1 943 | 4.63 | 166.80 | -5 298 | 1.70 | -101.44 | -1 937 | 4.51 |
| 2 | -36.76 | -1 973 | 4.56 | 155.75 | -5 300 | 1.70 | -101.75 | -1 999 | 4.38 |
| 3 | -33.91 | -1 989 | 4.52 | 150.04 | -5 284 | 1.70 | -98.60 | -2 029 | 4.34 |
| 注:轴力受压为正,弯矩内侧受拉为负. | |||||||||
| 衬砌厚度/m | 水压力/Pa | 折减系数 | 渗透量/(m2·(s·m-1)-1) | ||||
| 分析点1 | 分析点2 | 分析点3 | 理论值 | 数值解 | 理论解 | ||
| 0.3 | 2.79×105 | 3.21×105 | 3.87×105 | 2.97×105 | 0.71 | 4.80×10-4 | 4.44×10-4 |
| 0.6 | 3.35×105 | 3.72×105 | 4.60×105 | 3.49×105 | 0.83 | 2.84×10-4 | 2.66×10-4 |
| 0.9 | 3.57×105 | 4.00×105 | 4.93×105 | 3.70×105 | 0.88 | 2.08×10-4 | 1.92×10-4 |
| 衬砌半径/m | 分析点1 | 分析点2 | 分析点3 | ||||||
| 弯矩/(kN·m) | 轴力/kN | 安全系数 | 弯矩/(kN·m) | 轴力/kN | 安全系数 | 弯矩/(kN·m) | 轴力/kN | 安全系数 | |
| 0.3 | -6.12 | -1 099 | 4.09 | -43.54 | -3 536 | 1.27 | 2.75 | -1 037 | 4.34 |
| 0.6 | -18.53 | -1 823 | 4.94 | 187.84 | -5 255 | 1.71 | -68.47 | -1 708 | 5.23 |
| 0.9 | 68.22 | -2 353 | 5.74 | -337.37 | -6 195 | 2.17 | 245.54 | -2 327 | 5.38 |
| 注:轴力受压为正,弯矩内侧受拉为负. | |||||||||
由表 3、4可知,在工况1中注浆半径和衬砌半径不变的情况下:
1) 有水较无水情况下荷载大,随着渗透系数的减小,不透水情况下的内力最大,最不利位置均出现于拱腰处;衬砌由透水逐渐过渡为不透水的过程中,拱腰内力减小,其安全系数增大了7.8%,而对拱顶和仰拱存在不利,安全系数分别减小了10.4%和6.3%.
2) 衬砌渗透系数减小,渗透量减小,水压力增大;当衬砌不透水时,衬砌上的水压力全部为静水压力,不进行折减;渗透量和折减系数以及水压力和埋深的关系满足公式(4);渗透系数每减小10倍,水压力依次增大85.9%、60.7%、15.5%,渗透量依次减小29.3%、74.4%、88.2%.
3) 随着渗透系数的减小,水压力与渗透量的数值解与解析解的误差分别为5.2%、4.2%、5.9%、7.0%和7.5%、6.3%、6.4%、7.4%.
以衬砌渗透系数作为横坐标轴,折减系数与渗透量分别作为主要纵坐标轴和次要纵坐标轴,绘制关于3者的关系曲线,见图 4.
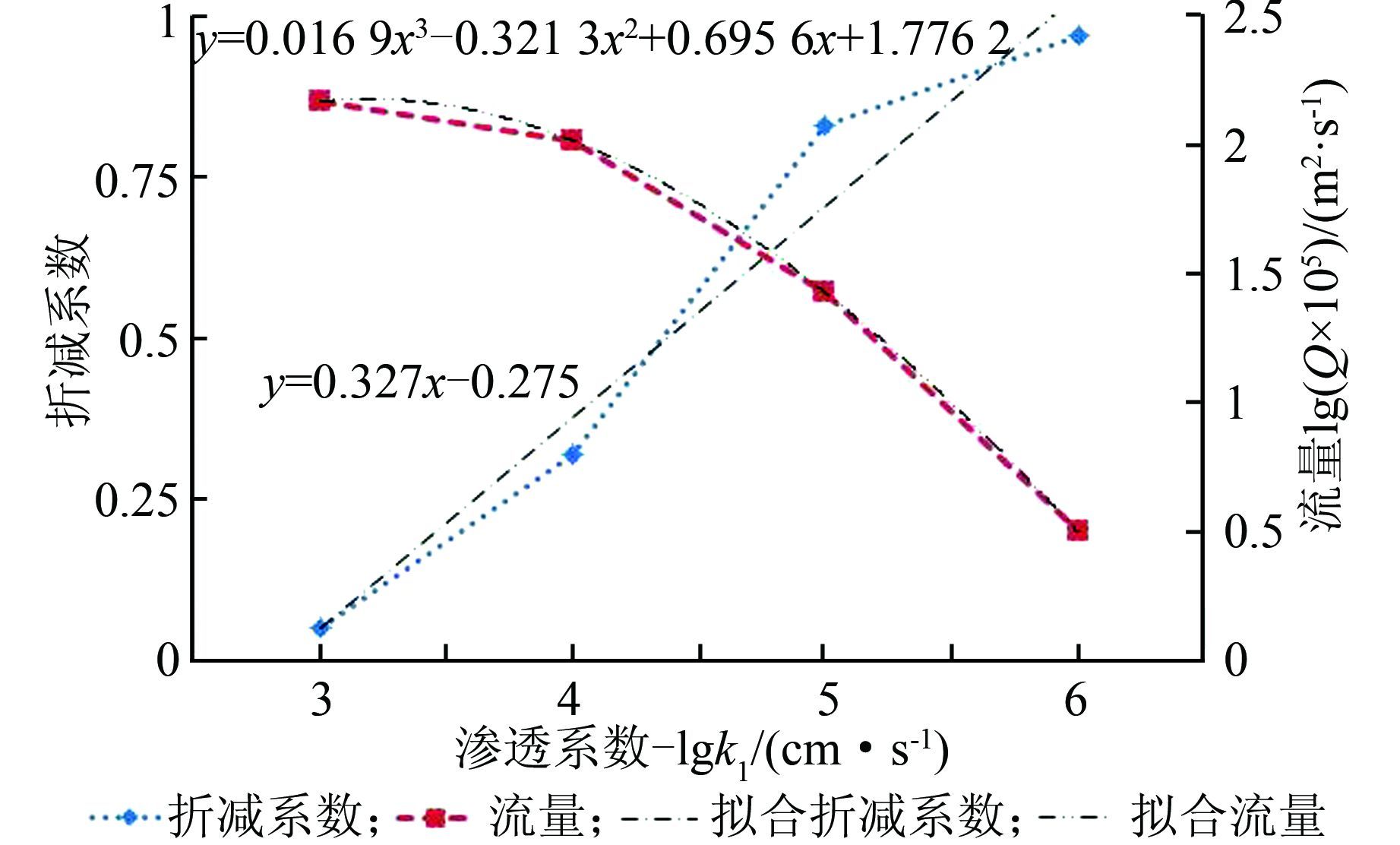
|
| 图 4 衬砌渗透系数与渗透量和折减系数的关系曲线 Figure 4 The relationship among the permeability coefficient of lining,flow and the reduction coefficient |
由图 4可知,位于不透水与透水之间的渗透系数,与相应情况下的折减系数与渗透量满足一定关系,可通过拟合曲线插值直接得到各个渗透系数下的折减系数与渗透量.
由表 5、6可知,在工况2中衬砌渗透系数与衬砌半径不变的情况下:
1) 随着注浆半径的增大,水压力减小,衬砌的安全系数改变不明显,但趋势均为减小;拱腰处安全系数变化最小.
2) 注浆半径每增加1 m,则渗透量依次减小10.2%、8.4%、6.8%,水压力依次减小10.0%、8.3%、6.9%.
3) 该工况下水压力与渗透量的数值解与解析解误差分别为6.4%、5.4%、5.0%、4.6%和6.3%、5.5%、4.8%、4.7%.
以注浆半径作为横坐标轴,折减系数与渗透量分别作为主要纵坐标轴和次要纵坐标轴,绘制关于3者的关系曲线,见图 5.
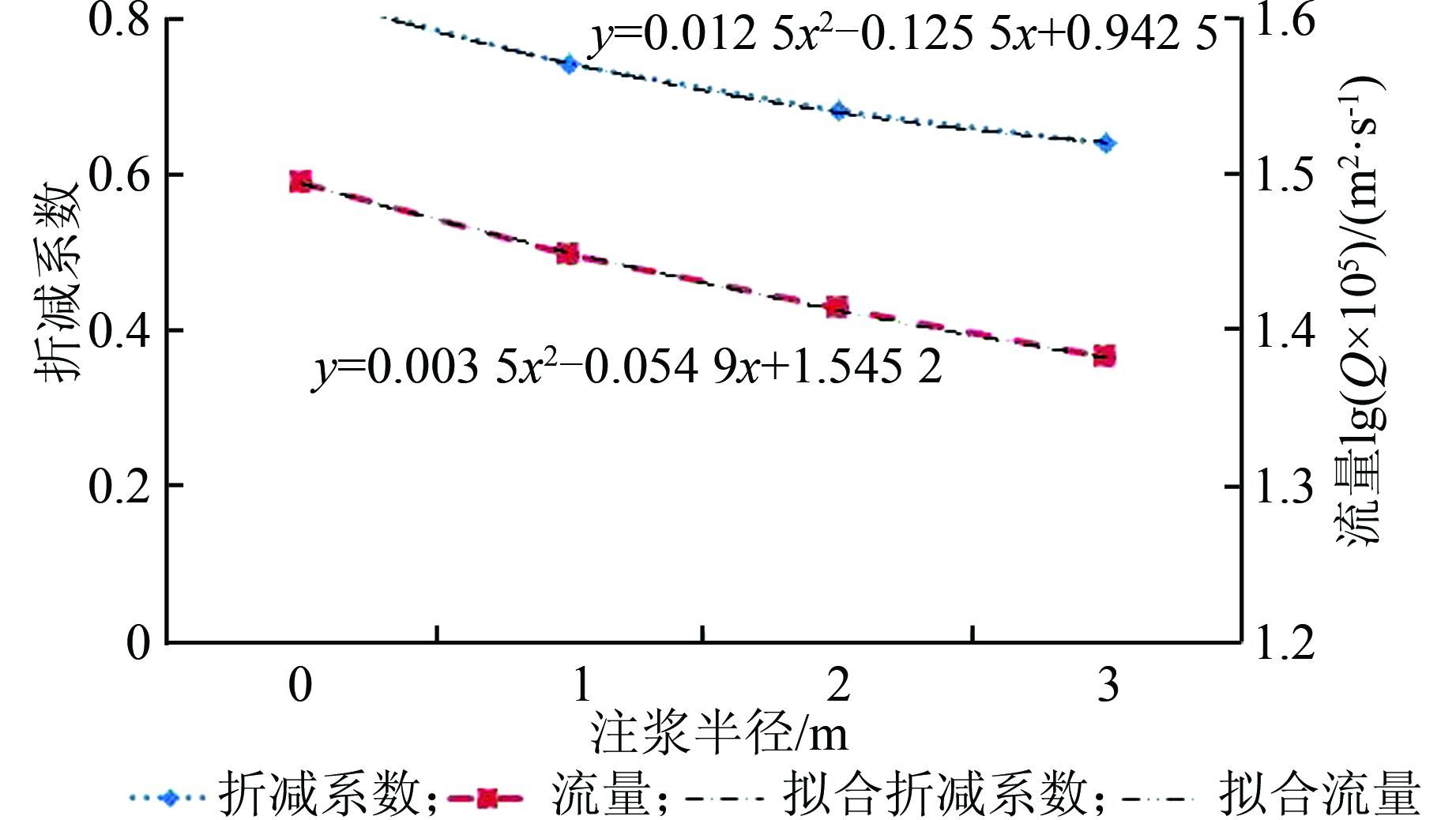
|
| 图 5 注浆半径与渗透量和折减系数的关系曲线 Figure 5 The relationship among the grouting radius,flow and the reduction coefficient |
由图 5可知:注浆半径由0逐渐增大到3 m,与相应情况下的折减系数与渗透量满足一定关系.当注浆半径未达到令渗透量稳定的数值时[13],可以通过拟合曲线插值直接得到各个注浆半径下的折减系数与渗透量.
由表 7、8可知,在工况3中衬砌渗透系数与注浆半径不变的情况下:
1) 衬砌厚度增大,安全系数随之增大;最不利位置拱腰(分析点2)的安全系数依次增大25.7%、21.2%.
2) 随着衬砌厚度的增大,渗透量减小,水压力增大,折减系数增大;衬砌厚度每增加0.3 m,则水压力依次减小14.9%、5.7%,渗透量依次减小40.1%、27.8%.
3) 该工况下水压力与渗透量数值解与解析解的误差分别为7.5%、6.2%、7.5%和7.5%、6.3%、7.7%.
4 结论通过将马蹄形隧道等效为圆形隧道的方式,对轴对称解析解计算和有限差分法FLAC3D数值计算,可以得到在不同衬砌渗透系数、不同注浆半径以及不同衬砌半径的情况下,衬砌所受水压力、渗透量、衬砌内力的数据及水压力与渗透量数值解与解析解的误差,并对其加以分析,得到以下关于马蹄形隧道衬砌与水压力结论:
1) 衬砌不透水,无需对水压力进行折减;
2) 3种工况下,最不利位置均在拱腰处;衬砌渗透系数由透水至不透水,拱腰处安全系数增大7.8%,拱顶与仰拱处减小10.4%和6.3%;注浆半径的增大对衬砌安全系数没有显著的改变;衬砌厚度的增大,拱腰处安全系数依次增大了25.7%、21.2%;
3) 渗透系数每减小10倍,水压力会依次增大85.9%、60.7%、15.5%,渗透量依次减小29.3%、74.4%、88.2%;注浆半径每增加1 m,渗透量依次减小10.2%、8.4%、6.8%,水压力依次减小10.0%、8.3%、6.9%;衬砌厚度每增加0.3 m,水压力依次减小14.9%、5.7%,渗透量依次减小40.1%、27.8%;
4) 在3种工况下,水压力与渗透量的数值解与解析解误差最大值为7.7%,误差较小,验证了轴对称解析解简化马蹄形断面计算隧道衬砌水压力荷载及渗透量的方法.
通过以上结论,得到了马蹄形隧道在不同渗透系数、注浆半径和衬砌厚度的衬砌水压力、内力和渗透量的变化规律,并验证了轴对称解析解简化马蹄形断面计算隧道衬砌水压力及渗透量的方法.
| [1] |
铁道第二勘察设计院.TB10003-2005 铁路隧道设计规范[S].北京:中国铁道出版社,2005.
The Second Railway Survey and Design Institute Group Corporation. TB10003-2005 Code for Design of Railway Tunnel[S]. Beijing: China Railway Publishing House , 2005. |
| [2] |
北京城建设计研究总院.GB50157-2003 地铁设计规范[S].北京:中国计划出版社,2003.
Beijing Urban Engineering Design & Research Institute. GB50157-2003 Code for Design of Metro[S].Beijing: China Planning Press, 2003. |
| [3] |
重庆交通科研设计院.JTG D70-2004 公路隧道设计规范[S].北京:人民交通出版社,2004.
Chongqing Communications Research and Design Institute. JTG D70-2004 Code for Design of Highway Tunnel[S]. Beijing : China Communications Press , 2004. |
| [4] |
水利部东北勘测设计研究总院.SL279-2002 水工隧道设计规范[S].北京:中国水利水电出版社,2004.
Northeast Investigation and Design Institute of Water Conservancy. SL279-2002 Specification for Design of Hydraulic Tunnel[S]. Beijing: China Water Power Press , 2004. |
| [5] |
王建秀, 杨立中, 何静. 深埋隧道衬砌水荷载计算的基本理论[J].
岩石力学与工程学报, 2002, 21(9): 1339–1343.
Wang Jianxiu, Yang Lizhong, He Jing. Introduction to the calculation of external water pressure of tunnel lining[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(9): 1339–1343. |
| [6] |
李伟, 杨丹, 李庆. 高水压山岭隧道衬砌结构水压力特征研究[J].
铁道工程学报, 2013, 182(11): 57–61.
Li Wei, Yang Dan, Li Qing. Study on the characteristic of water pressure upon lining in subject to high hydraulic pressure mountain tunnel[J]. Journal of Railway Engineering Society, 2013, 182(11): 57–61. |
| [7] |
李鹏飞, 张顶立, 赵勇, 张成平. 海底隧道复合衬砌水压力分布规律及合理注浆加固圈参数研究[J].
岩石力学与工程学报, 2012, 31(2): 280–288.
Li Pengfei, Zhang Dingli, Zhao Yong, Zhang Chengping. Study of distribution law of water pressure acting on composite lining and reasonable parameters of grouting gircle for subsea tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 280–288. |
| [8] |
郑波, 王建宇, 吴剑. 基于等效渗透系数计算衬砌水压力方法研究[J].
现代隧道技术, 2011, 48(12): 43–46.
Zheng Bo, Wang Jianyu, Wu Jian. Study of the calculation of external water pressure on tunnel lining based on the equivalent permeability coefficient of the composite lining[J]. Modern Tunnelling Technology, 2011, 48(12): 43–46. |
| [9] |
张民庆, 黄鸿健, 苗德海, 田四明. 岩溶隧道水压力的研究与确定[J].
铁道工程学报, 2008, 116(5): 53–58.
Zhang Minqing, Huang Hongjian, Miao Dehai, Tian Siming. Study on and determination of water pressure of the karst tunnel[J]. Journal of Railway Engineering Society, 2008, 116(5): 53–58. |
| [10] |
李苍松, 胡元芳, 丁建芳, 等. 隧道地下水处治的设计理论及方法研究[J].
工程地质学报, 2012, 20(5): 832–839.
Li Changsong, Hu Yuanfang, Ding Jianfang, et al. Research on design theory and methodology for tunnel groundwater treatment[J]. Journal of Engineering Geology, 2012, 20(5): 832–839. |
| [11] |
何明磊, 胡磊, 孟祥磊. 隧道衬砌水压力荷载及内力研究[J].
铁道标准设计, 2014, 58(2): 79–83.
He Minglei, Hu Lei, Meng Xianglei. Research on water pressure load and internal force of tunnel lining[J]. Railway Standard Design, 2014, 58(2): 79–83. |
| [12] |
郑波, 王建宇, 吴剑. 轴对称对隧道衬砌水压力计算的适用性研究[J].
现代隧道技术, 2012, 49(1): 61–65.
Zheng Bo, Wang Jianyu, Wu Jian. A Study of the applicability of an axisymmetric solution for calculating the water pressure on a tunnel lining[J]. Modern tu Tunnelling Technology, 2012, 49(1): 61–65. |
| [13] |
李鹏飞, 张顶立, 周烨. 隧道涌水量的预测方法及影响因素研究[J].
北京交通大学学报, 2010, 34(4): 11–15.
Li Pengfei, Zhang Dingli, Zhou Ye. Study on prediction methods and its influence factors of water inflow into tunnels[J]. Journal of Beijing Jiaotong University, 2010, 34(4): 11–15. |
 2016, Vol. 49
2016, Vol. 49



