文章信息
- 鲜杏, 范传光, 文闪闪, 王有春, 陈聪, 刘欣
- XIAN Xing, FAN Chuanguang, WEN Shanshan, WANG Youchun, CHEN Cong, LIU Xin
- 考虑可再生能源随机性的孤岛微网容量优化配置方法
- Optimal deployment for island microgrid considering probabilistic factors of renewable energy generations
- 武汉大学学报(工学版), 2016, 49(1): 100-104
- Engineering Journal of Wuhan University, 2016, 49(1): 100-104
- http://dx.doi.org/10.14188/j.1671-8844.2016-01-017
-
文章历史
- 收稿日期: 2015-05-11
2. 武汉大学电气工程学院, 湖北 武汉 430072
2. School of Electrical Engineering, Wuhan University, Wuhan 430072, China
由于地理因素和建设成本等问题,在海岛、山村等偏远地区仍存在大量由柴油机供电的孤岛电网.随着这类地区化石燃料的日益紧缺和公众环保意识的逐渐加强,有必要在这类地区发展以可再生能源发电为主的微网[1, 2].
孤岛运行的微网中分布式电源出力存在不确定性,系统惯性小,电力电量平衡的难度较大,因此微网容量优化配置问题是微网规划与设计的关键问题之一.该问题与出力较稳定的传统类型分布式电源优化配置问题的区别主要体现在于微网内部可再生能源发电的随机性上[3, 4].
在微网容量优化配置领域,目前国内外学者取得了一些理论和实践方面的成果[5, 6].文献[7]考虑了分布式发电接入对配网潮流和线路负载率的影响,建立了含分布式电源的配网扩展规划的实用数学模型;文献[8]系统地提出了分布式发电系统的规划设计、运行和保护等问题,均可延伸至微网领域;文献[9]使用模糊C均值聚类处理大量的初始数据,采用基于马尔可夫链的遗传算法,对孤岛微网容量进行优化;文献[10]以年风速、气温、光照强度作为基础数据,考虑了经济性、可靠性等因素的协调,建立了孤岛微网的容量优化配置模型;文献[11]对含微网的复杂配电网进行了可靠性评估,并依次实现了微电源的位置和容量规划.文献[5-8]均未考虑风能、太阳能发电的随机性对微网中分布式电源容量优化配置带来的影响,一般只将可再生能源发电作为固定出力的电源.
综上所述,目前微网容量优化配置问题对微网内部随机性因素考虑不足.针对这一问题,本文首先对微网内部随机性因素进行建模,利用蒙特卡洛(Monte Carlo)随机模拟的方法获取随机性出力电源出力与负荷容量;在此基础上,建立了微网容量优化配置数学模型,以总投资最少为目标函数,以碳排放量和供电可靠性等指标为约束条件,采用遗传算法求解,实现了微网容量的优化配置.
1 微网内部随机因素模拟 1.1 蒙特卡洛模拟蒙特卡洛模拟即随机模拟,是从给定的概率分布中抽取随机变量,重复该过程以对系统决策进行检验或为系统决策提供依据[12].
1.2 风力发电机出力随机模型威布尔分布被普遍认为是与实测风速分布拟合较好的概率模型,其概率密度分布为
式中:v为风速;α>0,为形状参数,无单位;β>0,为尺度参数;δ<vmin,为位置参数,二者可由风速的平均值和标准差获得:
已知风速时,利用风力发电机出力与风速关系可得其出力:
式中:pr为风力发电机组的额定功率;vr为额定风速;vci为切入风速;vco为切出风速.
进行蒙特卡洛模拟时,利用当地经纬度信息在NSDR气象网站查询每月平均风速所生成每小时风速,根据公式(2) 、(3) 得到每天风速的平均值和标准差,进而获取威布尔分布参数,代入式(1) ,利用蒙特卡罗方法随机产生风速数据,并根据式(4) 计算风机的随机有功出力.
1.3 光伏电池出力随机模型据统计,在数小时尺度内,光照强度可以近似看成贝塔分布,其概率密度函数如下:
式中:r和rmax分别为该时间段内的实际光照强度和最大光照强度;α和β均为贝塔分布的形状参数,可由光照强度的平均值和标准差近似求出:
光伏电池方阵有功出力的简化计算公式为
式中:A为方阵的总面积;η为方阵总的光电转换效率.已知光照强度的概率密度函数,利用式(8) 可得光伏有功出力的概率密度函数:
进行蒙特卡洛模拟时,首先利用当地经纬度在NSDR气象网站查询每月平均光照强度所生成每小时光照强度,得到每天光照强度的平均值和标准差,从而根据公式(6) 、(7) 获取贝塔分布参数,再根据式(9) ,利用蒙特卡罗方法随机产生风机的随机有功出力.
1.4 负荷随机模型长期实践中验证了用电负荷的分布近似满足正态分布,其概率密度函数为
式中:PL为用电负荷功率;μP和δP分别为用电负荷的平均值和标准差.
进行蒙特卡洛模拟时,首先利用历史用电负荷数据获取其平均值与标准差,再利用式(10) 根据蒙特卡罗方法随机产生用电负荷的模拟容量.
2 微网容量优化配置方法 2.1 微网容量优化配置目标函数在本文所提出的微网容量优化配置方法中,以经济性最佳建立目标函数.微网成本包括机组成本、安装成本和运行成本.对于风力发电和光伏太阳能发电等可再生能源,运行成本可以忽略.对于柴油发电机,在功率平衡策略中处于次要地位,因此其成本计算需要经过功率平衡计算其燃料耗量后进行.
以风、光、柴微网为例,这种微网建设时的成本最小目标函数为
式中:N和C分别表示3种分布式电源的数目和成本;数字1、2和3分别代表机组成本、安装成本和运行成本.
2.2 微网容量优化配置约束条件在孤岛微网正常运行的基础上,考虑实际情况,综合协调可靠性和环保因素,微网容量优化配置的主要约束条件有
1) 电力电量平衡
本文以1 h为时间尺度建立微网电力电量平衡约束:
式中,Nx,i,t表示各种分布式电源在规划时间t时的电源出力,本文中的规划时间尺度设为1,从而避免考虑各种发电机的动态运行情况.
2) 微网中分布式发电最多和最好的数量限制如下:
3) 供电可靠性约束
常用的可靠性指标有最小缺电概率LO,全年负载缺电率LP等[11],本文中采用LO:
4) 环保因素约束
柴油发电机的经济模型除了安装成本和维护成本外,还包括燃油运行成本.柴油发电机发电过程中会排放二氧化碳(CO2).燃料耗量和CO2排放量均可以表示为柴油机输出功率的二次函数[17]:
则柴油机经济模型为
相对于其他类型分布式发电,柴油发电机的响应速度较快,由于本文中的时间尺度为1 h,因此在此忽略1 h内柴油发电机输出功率的变化情况.
2.3 模型求解方法在蒙特卡洛模拟获得各类分布式电源的每小时出力数据和用电负荷的每小时数据之后,以各类分布式电源的装机数目为决策变量,利用遗传算法进行求解.首先将决策变量进行十进制编码,把目标函数作为适应度函数,在约束条件筛选的限制下,通过复制、遗传和变异,最终实现种群的进化和目标函数值最小.
在遗传算法实现过程中,取种群数为50,迭代次数为100,交叉率和变异率初设为0.75和0.1,并随种群多样性调整.选择操作采用轮盘赌的方法.
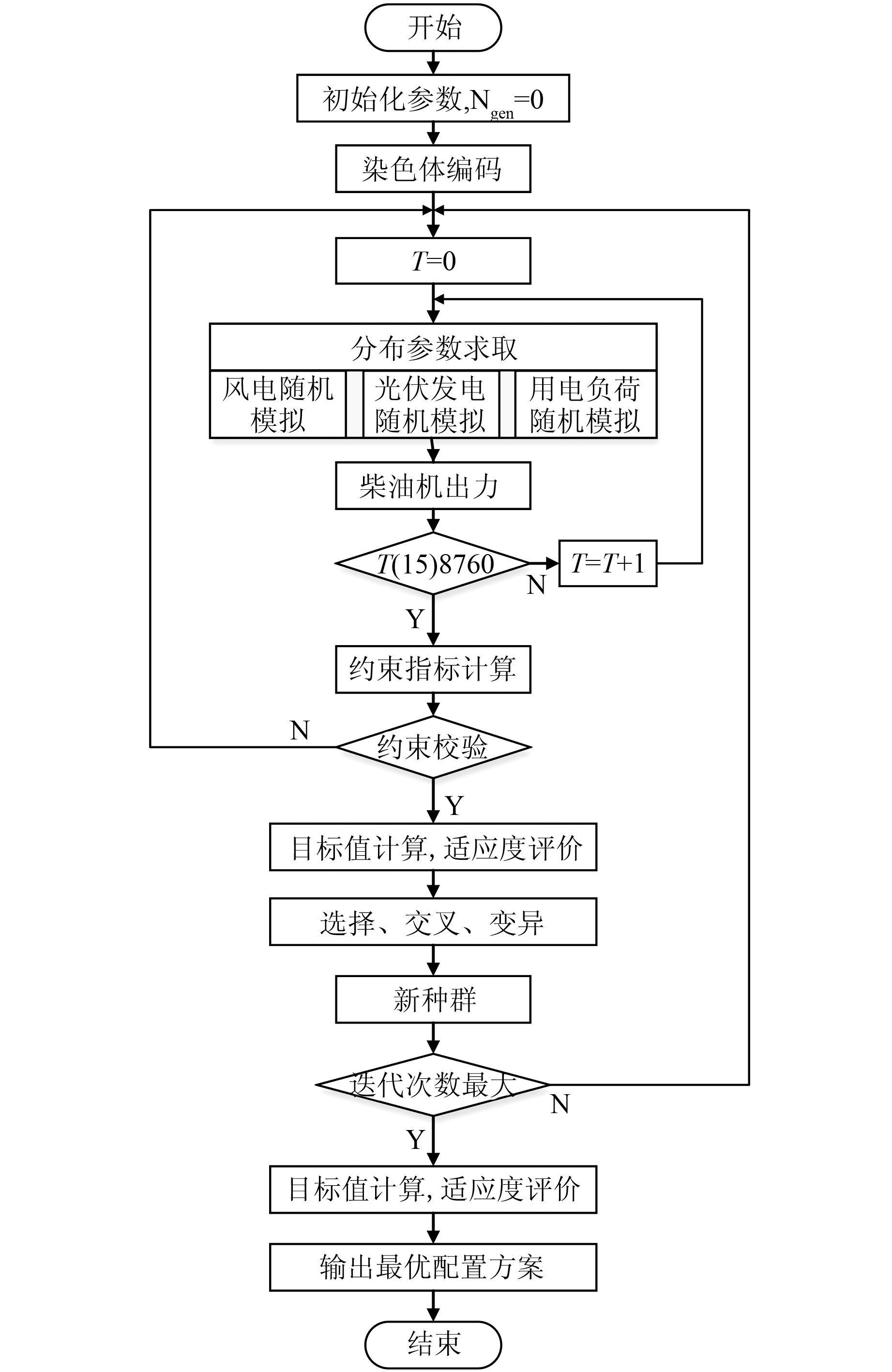
本文所提出的微网容量优化配置方法的系统流程如图 1所示.其中,Ngen表示种群迭代次数,T表示一年中的时间,单位为1 h.风力发电和光伏发电的随机模拟为单机模拟,且不考虑机组之间的出力相关性;由分布式电源随机模拟与用电负荷随机模拟之差得到柴油机运行情况,进而获取LO、碳排放量等指标结果.目标函数中,柴油机运行成本结果参与全年迭代过程,这是模型求解的一个难点.
|
| 图 1 微网的容量优化配置流程图 Figure 1 Flow chart for optimal sizing of microgrid |
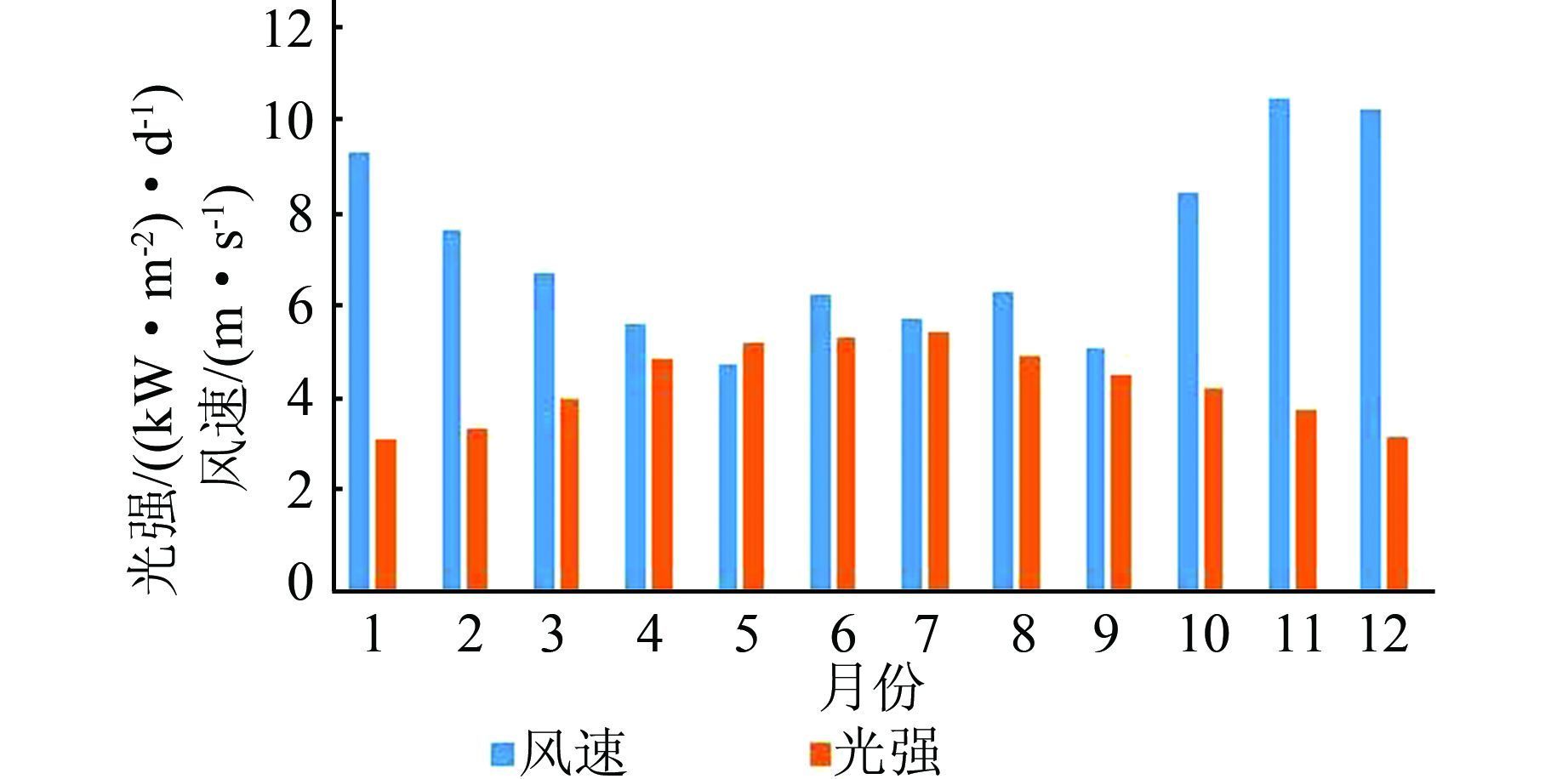
某海岛地区具有较为丰富的风资源和日照资源,在案例分析前,主要由柴油机发电供电.该岛月平均天气数据如图 1所示,容易看出该地区风光资源具有明显的互补特性.
|
| 图 2 月平均风速与光强 Figure 2 Monthly avergage wind speed and solar radiation |
|
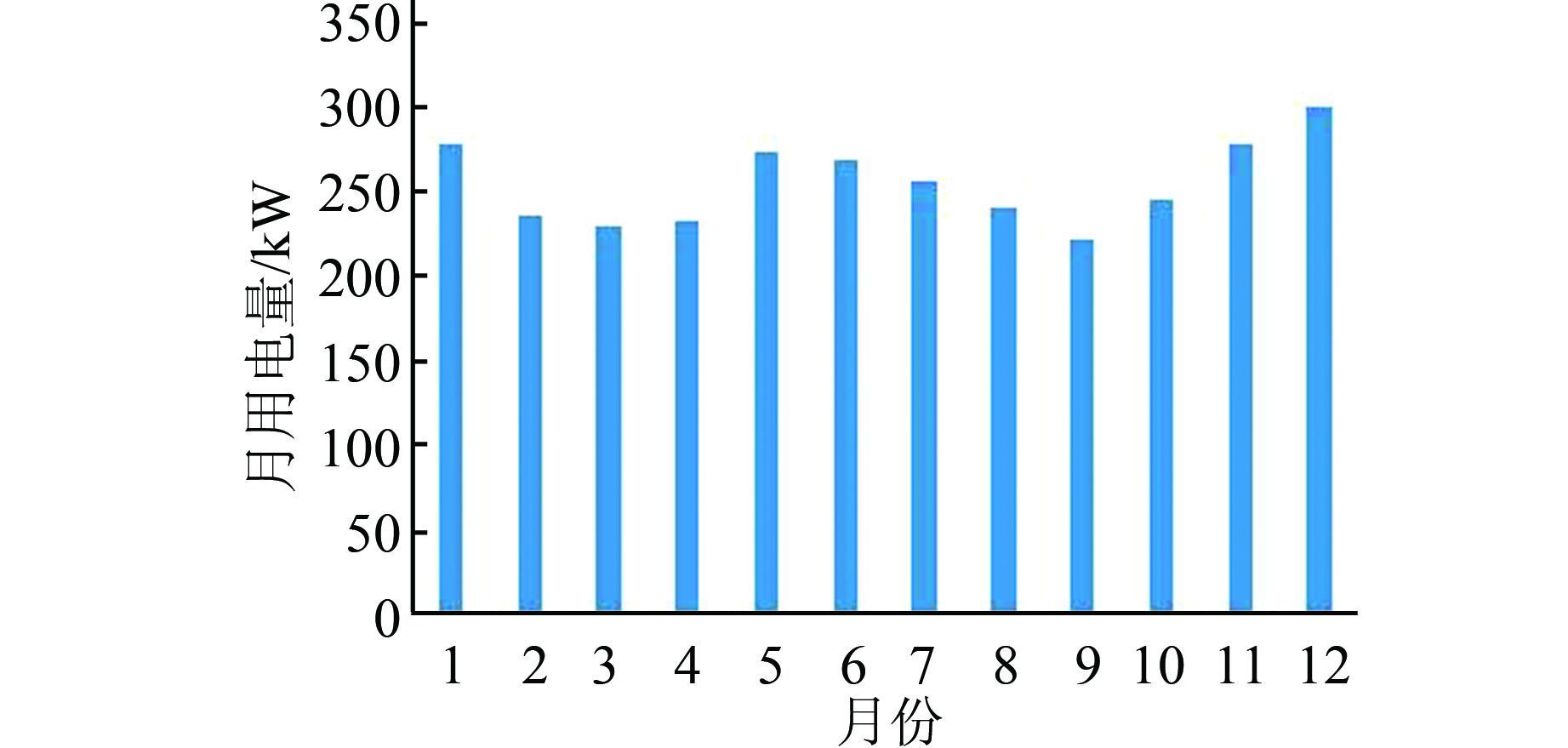
| 图 3 每月平均用电负荷功率 Figure 3 Monthly average load power |
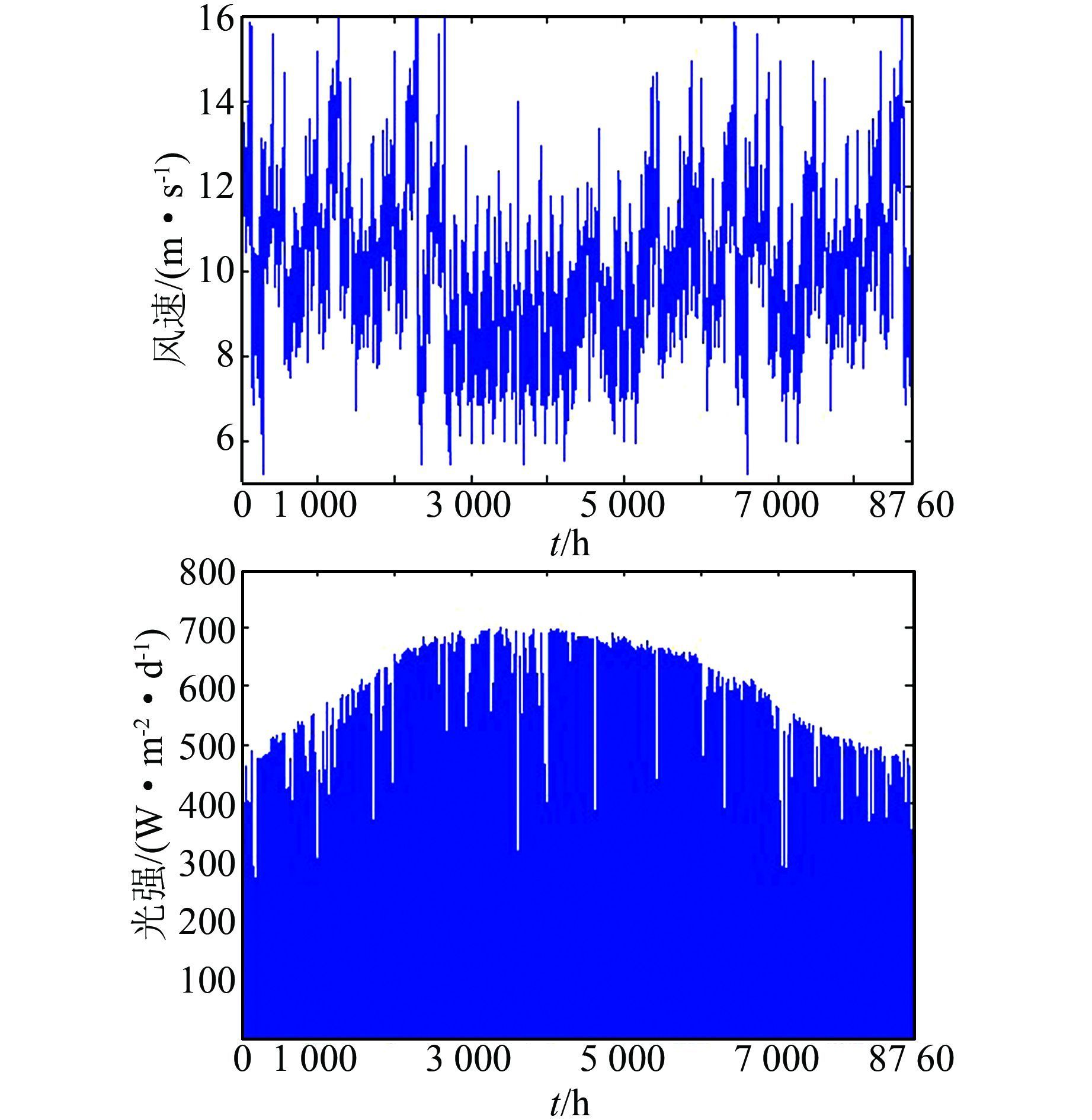
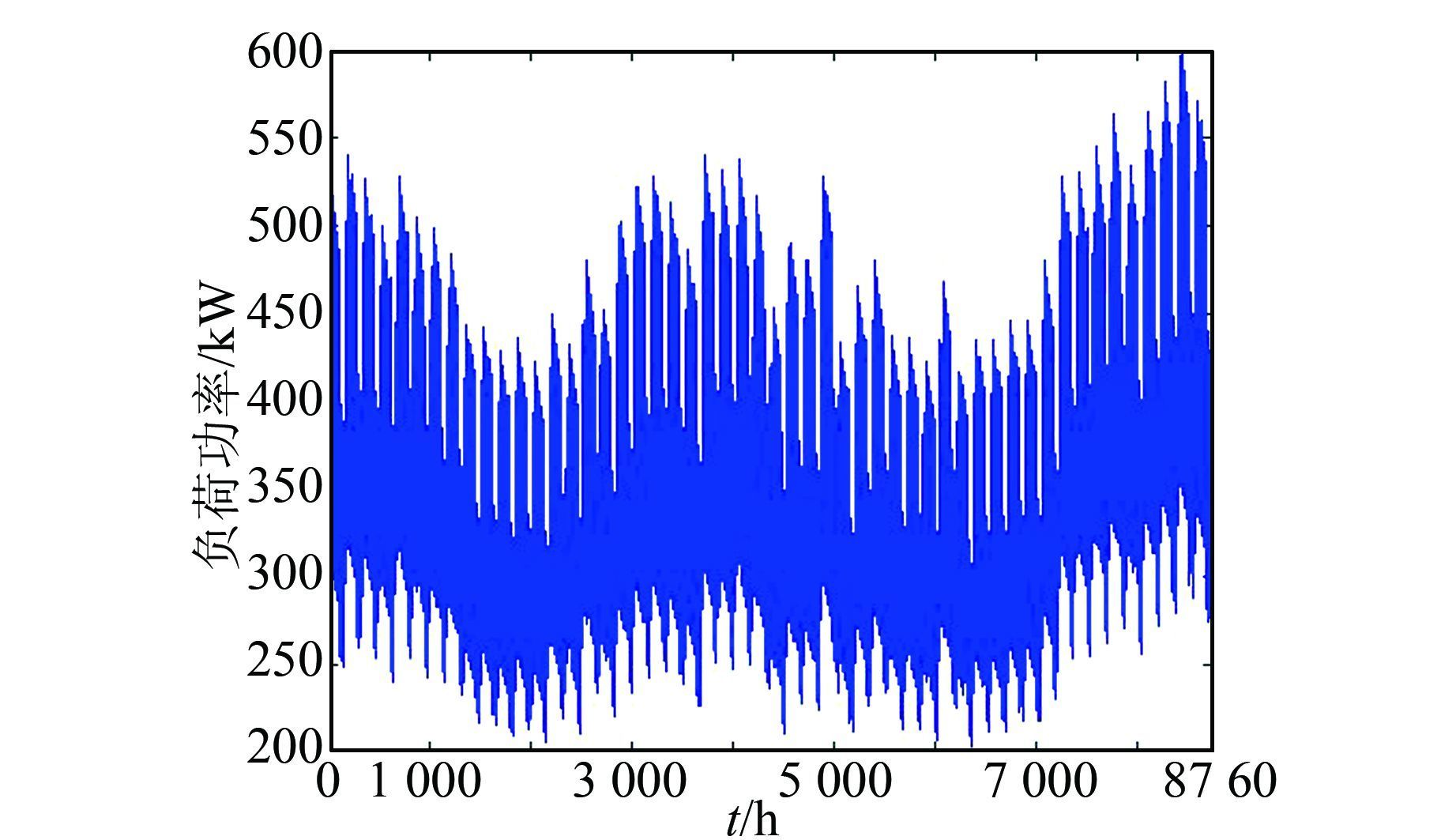
利用第1节所述方法,根据风速、日照和负荷平均数据,即可得到各种随机因素分布函数所对应的分布参数,对各个分布函数分别使用蒙特卡罗模拟,得到全年8 760 h的风速、光照强度和用电负荷数据,如图 4、5所示.
|
| 图 4 年风速与日照模拟 Figure 4 Simulation of annual wind speed and solar radiation |
|
| 图 5 年用电负荷模拟 Figure 5 Simulation of annual electricity comsumption |
分布式电源成本参数见表 1,其中,机组型号最后的数字代表其额定功率,单位为kW.风机切入、额定和切出风速分别为2.5、12和15 m/s.
| 机组名 | 型号 | 单位功率成本/($·kW-1) | 安装成本/($·kW-1) | 维护成本/($·kW-1) |
| 柴油机 | DE-K-60 | 300 | 3 250 | 0.02 |
| 风机 | WD-10 | 2 805 | 450 | 0.06 |
| 光伏电池 | MSX-83 | 5 175 | 1 500 | 0 |
在蒙特卡洛模拟获得各类分布式电源的每小时出力数据和用电负荷的每小时数据之后,以各类分布式电源的装机数目为决策变量,利用遗传算法对该问题进行求解,得到的最终决策变量结果见表 2.
案例地区风光资源均较为丰富,图 1中也可以明显看出风光资源的互补性,有利于提升可再生能源发电利用率,减少柴油发电机运行时间.
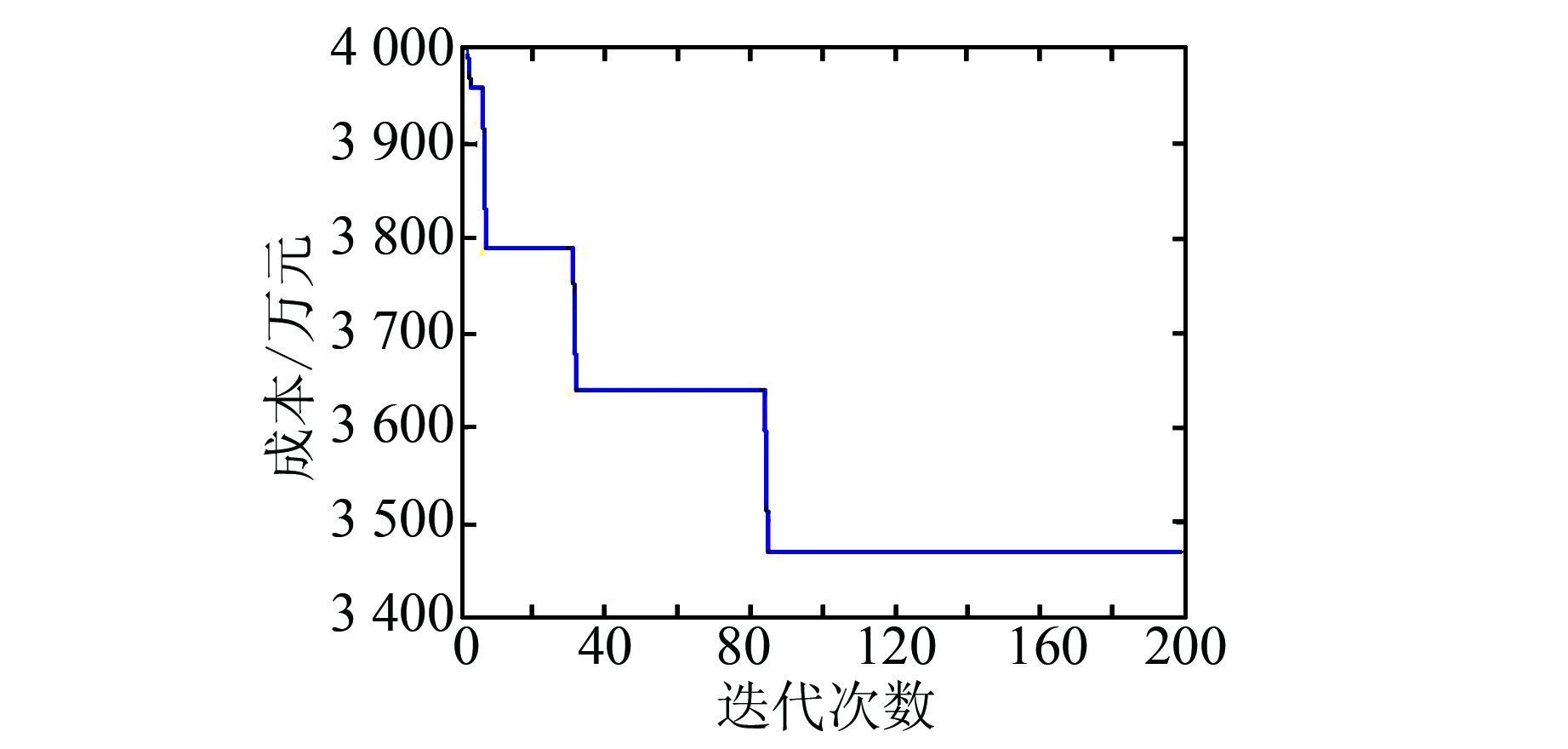
目标函数的收敛情况如图 6所示.从图中可知,算法可以快速寻找到最优解,当系统可靠性设置为0.005时,最佳成本为3 470万元.
|
| 图 6 收敛曲线 Figure 6 Curve convergence |
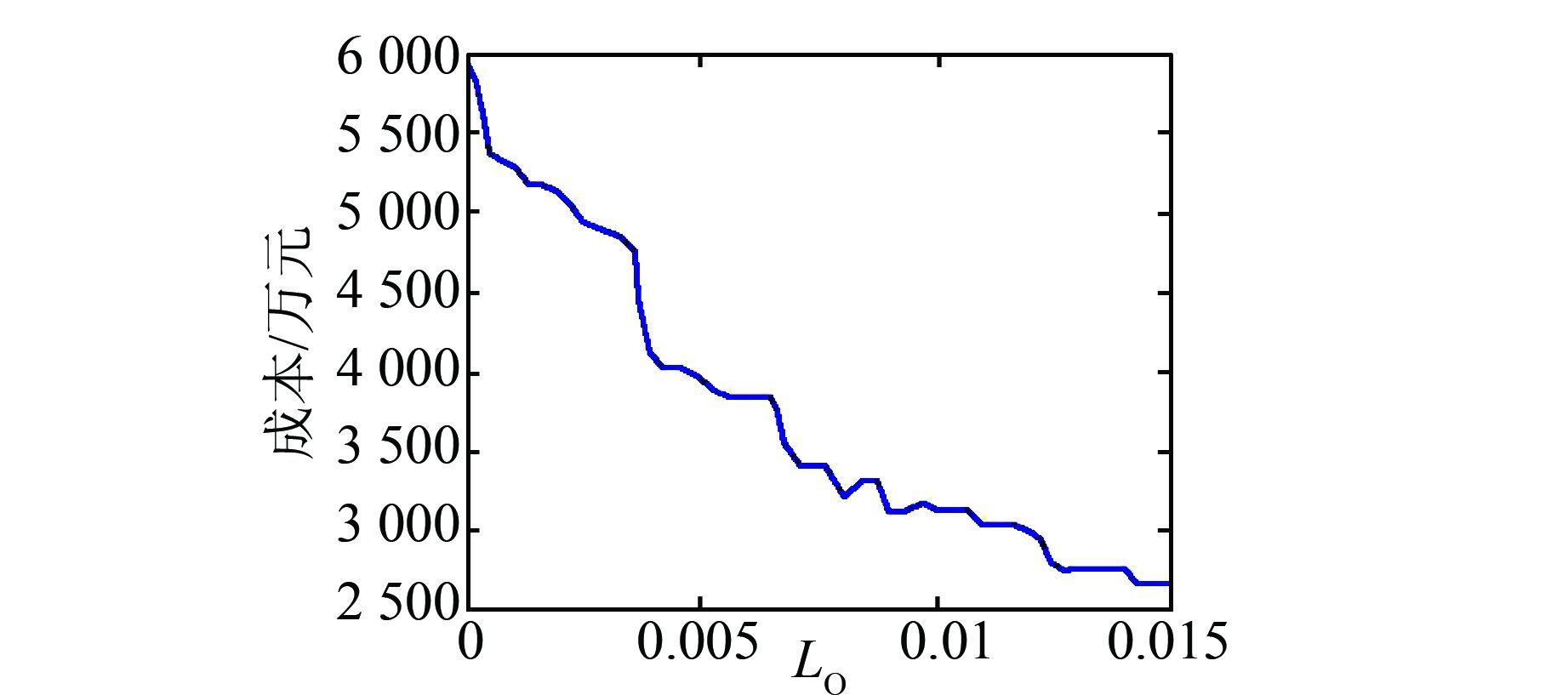
微网年投资费用变化较大,高供电可靠性会带来高经济性代价,当系统最小缺电概率LO在0~0.015之间时,LO与成本灵敏度关系见图 6.
由图 7可知,随着可靠性指标LO的增大,系统的供电可靠性变差,但微网的总体经济性也会显著降低,说明系统可靠性的改善需要以增大投入为代价;并且在容量配置投资成本足够大时,可以完全保证孤岛微网的可靠供电,但此时的经济性不理想.在孤岛微网系统容量配置的工程实践中,应当根据用电负荷的重要性和具体情况,在系统充裕性不足时,允许中断部分非重要负荷,即根据满足一定的LO约束条件,选取最优的电源容量组合,从而在保证系统可靠性的同时,尽可能地保证系统的经济性.
|
| 图 7 可靠性指标与成本灵敏度关系 Figure 7 Relationship between reliable |
微网容量配置时必须考虑其内部随机性因素,应用本文方法,得出以下结论:
1) 独立海岛地区微网可采用风光互补的方式供电,在保证当地供电可靠性的同时,提高可再生能源利用率,减少柴油机发电运行时间.
2) 微网随机性主要体现在可再生能源发电出力不确定性上,通过历史数据获取分布参数,利用蒙特卡洛模拟的方法可以有效解决该问题.
3) 随着LO的降低,系统的供电可靠性改善,但由于电源配置的增加导致综合成本费用也会显著增加,系统可靠性的提高需要以增大投资为代价;并且在容量配置足够大时,可以完全保证可靠供电,但此时的成本费用会很高.
| [1] | Lasseter R H. MicroGrids [C]// 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings, 2002, 1: 305-308. |
| [2] | Lasseter R H. Microgrid: A conceptual solution [C]// IEEE 35th Annual Power Electronics Specialists Conference, 2004: 4285-4290. |
| [3] |
徐迅, 高蓉, 管必萍, 等. 微电网规划研究综述[J].
电网与清洁能源, 2012, 28(7): 18–24.
Xu Xun, Gao Rong, Guan Biping, et al. Overview of research on planning of Micro-Grid[J]. Power System and Clean Energy, 2012, 28(7): 18–24. |
| [4] |
乔蕾, 段绍辉, 汪伟, 等. 独立微网系统优化规划设计方法综述[J].
电力系统及其自动化学报, 2013(02): 115–123.
Qiao Lei, Duan Shaohui, Wang wei, et al. Reviews on optimal methods for planning of stand-alone microgrid system[J]. Electric Power System and Its Automotion, 2013(02): 115–123. |
| [5] | Jiayi H, Chuanwen J, Rong X. A review on distributed energy resources and MicroGrid[J]. Renewable and Sustainable Energy Reviews, 2008, 12(9): 2472–2483. DOI:10.1016/j.rser.2007.06.004 |
| [6] | Ustun T S, Ozansoy C, Zayegh A. Recent developments in microgrids and example cases around the world—A review[J]. Renewable and Sustainable Energy Reviews, 2011, 15(8): 4030–4041. DOI:10.1016/j.rser.2011.07.033 |
| [7] |
王成山, 陈恺, 谢莹华, 等. 配电网扩展规划中分布式电源的选址和定容[J].
电力系统自动化, 2006, 30(03): 38–43.
Wang Chengshan, Chen Kai, Xie Yinghua, et al. Siting and sizing distributed generation in distribution network expansion planning[J]. Automotion of Electric Power System, 2006, 30(03): 38–43. |
| [8] | Driesen J, Katiraei F. Design for distributed energy resources[J]. IEEE Power and Energy Magazine, 2008, 6(3): 30–40. DOI:10.1109/MPE.2008.918703 |
| [9] | Arabali A, Ghofrani M, Etezadi-Amoli M, et al. Stochastic performance assessment and sizing for a hybrid power system of solar/wind/energy storage[J]. Sustainable Energy, IEEE Transactions on, 2014, 5(2): 363–371. DOI:10.1109/TSTE.2013.2288083 |
| [10] |
秦跃进, 王有春, 范黎, 等. 微网中分布式电源的容量优化配置方法[J].
武汉大学学报(工学版), 2014, 47(03): 359–364.
Qin Yuejin, Wang Youchun, Fan Li, et al. Optimal sizing method of distributed generations in a stand-alone MicroGrid[J]. Engineering Journal of Wuhan University, 2014, 47(03): 359–364. |
| [11] |
马溪原, 吴耀文, 方华亮, 等. 基于可靠性评估的微电网配置方法[J].
电力系统自动化, 2011, 35(09): 73–77.
Ma Xiyuan, Wu Yaowen, Fang Hualiang, et al. Allocation of microgrids based on reliability evaluation[J]. Automotion of Electric Power System, 2011, 35(09): 73–77. |
| [12] |
张红丽, 刘涤尘, 王波, 等. 基于蒙特卡罗算法的孤岛供电系统随机调度研究[J].
陕西电力, 2012, 40(06): 1–5.
Zhang Hongli, Liu Dichen, Wang Bo, et al. Study on stochastic dispatch for island power supply system based on Monte Carlo algorithm[J]. Shanxi Electric Power, 2012, 40(06): 1–5. |
| [13] | Hong Y, Lian R. Optimal sizing of hybridwind/PV/diesel generation in a stand-alone power system using Markov-based genetic algorithm[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 640–647. DOI:10.1109/TPWRD.2011.2177102 |
 2016, Vol. 49
2016, Vol. 49




