文章信息
- 程龙, 王涛, 漆鹏, 李永辉
- CHENG Long, WANG Tao, QI Peng, LI Yonghui
- 新庄铜铅锌矿含水层下防水矿柱留设计算分析
- Investigation of waterproof pillar design under aquifer in Cu-Pb-Zn mining of Xinzhuang
- 武汉大学学报(工学版), 2017, 50(3): 368-374
- Engineering Journal of Wuhan University, 2017, 50(3): 368-374
- http://dx.doi.org/10.14188/j.1671-8844.2017-03-008
-
文章历史
- 收稿日期: 2016-06-27
2. 中国石油大学(北京)石油工程教育部重点实验室,北京 102249;
3. 长沙矿山研究院有限责任公司,湖南 长沙 410012
2. Key Laboratory of Petroleum Engineering of Ministry of Education, China University of Petroleum (Beijing);
3. Changsha Institute of Mining Research, Co., Ltd., Changsha 410012, China
含水层下采矿要求矿井涌水量不超过其正常的排水能力,否则就会造成矿井水灾,影响矿井正常生产甚至导致人员的伤亡.因此,要防止由于开采形成的岩体损伤裂隙带波及到水体或含水层,这就需要留设防水矿柱,并根据计算确定允许的开采上限标高.防水矿柱可视为上覆岩层载荷以及水压力作用下的地下结构物,也是一种典型的可变形多孔介质.而突水是矿区防水矿柱失效的重要形式,不仅涉及到矿柱在水压力作用下的力学性质与长期稳定性问题,还涉及到流固耦合问题[1].
近年来,不受水体影响的矿产资源越来越匮乏,开采水体(包括含水层)下的矿产资源已经逐渐成为趋势.随着水体下开采煤矿的大幅度增加,上覆岩体的移动变形、破坏和导水裂隙带发育规律研究越来越受到人们的高度重视.水体下矿体的开采连同建筑物、路基(公路、铁路等)下矿体的开采合称为“三下”开采,其研究最早始于19世纪国外对保护教堂的需要[2].日本认为海下开采煤矿首要的安全措施是预留足够的防水煤矿柱;匈牙利煤矿区的水文地质复杂,含水灰岩多,溶洞发育,根据多年经验总结,提出了由采动引起的回采松动带高度的计算公式[3].
早期,由于我国采矿技术水平的限制,为保障安全而留设大尺寸的防水矿柱,给我国矿产资源造成较大程度的浪费.近几十年,伴随着开采技术水平的不断提高,我国的一些矿区进行了减小矿柱尺寸的开采,取得了不少经验.比如华东、华北、西北等地的许多煤矿,对防水煤矿柱的合理留设进行了深入研究[4-6].杨本水[7]等对中等含水层下留设防水煤矿柱的安全开采机理进行了研究,孟召平[8]等对第四系松散含水层下防水煤矿柱高度的确定方法进行了探讨,尹先尚[9]对防水煤矿柱留设对围岩变形的影响进行了数值模拟方面的研究,但他们大都是只考虑应力场而没有考虑渗流场的作用.
本文应用三维有限差分软件FLAC3D,结合江西省宜丰新庄铜铅锌矿区,考虑渗流场和应力场的共同作用,在保证回采充填区不会发生突水的情况下,对含水层下防水矿柱留设合理的尺寸进行研究.
1 FLAC3D中的流固耦合计算方法从渗流力学观点来看,土壤、岩石和混凝土均为孔隙介质或裂隙介质.FLAC3D模拟孔隙介质流体流动时,流体流动既可以独立于力学计算进行,又可以与力学计算耦合(即流固耦合计算),这样就可以考虑流体与岩土体之间的相互作用.流固耦合过程包含了两种力学现象:一是孔隙水压力的改变导致了有效应力的改变,从而影响土体的力学性能;二是土体中的流体会对土体体积的改变产生反作用,表现为流体孔压的变化[10].流固耦合计算主要由以下4个方程控制[11].
1) 平衡方程
流体平衡方程可以表示为
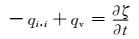 (1)
(1)
式中:qi为流体速度矢量在i方向分量,m/s;qv为流体体积源密度,L/s;ζ为由于流体扩散运动引起的单位体积孔隙介质流体质量变化量.
2) 运动方程
用Darcy定律来描述孔隙介质渗流过程中流体流速与孔隙水压力的关系.对均质的、各向同性的固体和常流体密度,运动方程可表示成如下形式:
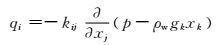 (2)
(2)
式中:kij为FLAD3D中的渗透系数k(m2/(Pa/s)),与渗透系数K(m/s)的关系,k=K/ρwgk;p为孔隙水压力,Pa;ρw为流体密度,kg/m3;gk为重力加速度分量.在FLAD3D中,对于饱和与非饱和流体,空气压力被认为是常数或等于0.
3) 本构方程
在FLAC3D公式描述中,假定流体质量的变化与孔隙水压力p、体积应变e、温度T的变化成线性关系,所以流体本构方程可以表示成:
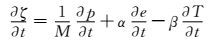 (3)
(3)
式中:M为Biot模量,N/m2;α为Biot系数;β为热膨胀系数,1/℃,用此来考虑流体和颗粒的热膨胀.
4) 相容方程
应变速率和速度梯度之间的关系为
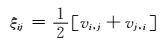 (4)
(4)
在FLAC3D流固耦合计算过程中,从初始力学平衡状态开始,要求水力耦合模拟的每一步包含一步或更多步的流体计算,直到满足静力平衡方程为止.由于流体的流动,孔隙压力增加在流体循环步中被计算,其对体积应变的贡献在力学循环步中被计算;然后,体积应变作为一个区域值被分配到各个节点上,从而实现流体与固体两者间的耦合.流固耦合问题分析中,引起系统平衡状态改变的因素包括力学边界条件(力学扰动)和流体边界条件(流体扰动).如果力学边界条件发生突变,分析的方法为:无渗流模式下,力学扰动后计算使系统达到静力平衡状态;然后,再计算随后的流固耦合响应.如果流体边界条件随着力学扰动的同时发生变化,分析的顺序为力学扰动、平衡状态、流体扰动、流固耦合分析.本文所采用的耦合模拟方法为:交替执行单渗流模式和单力学模式的计算时间步,通过设置平衡条件,控制系统进行力学与流体的循环计算,最终达到稳定平衡状态.
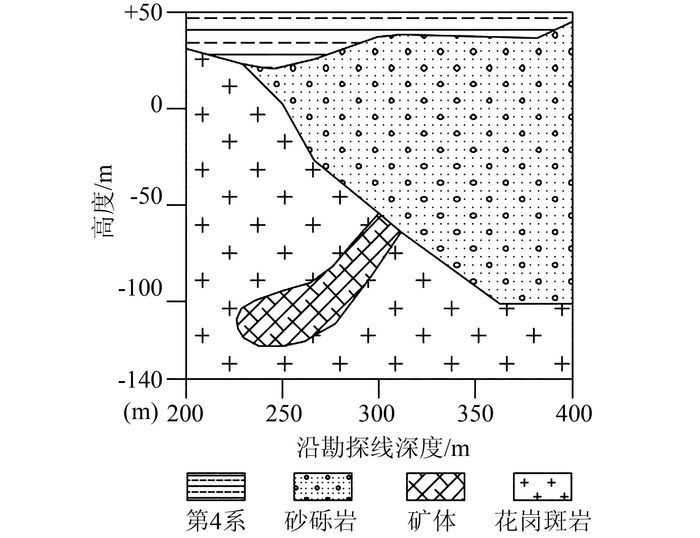
2 工程应用实例 2.1 工程概况江西省宜丰新庄铜铅锌矿区位于江西省宜丰县城东南面37 km处的宜丰县新庄镇口溪,图 1为17A号勘探线剖面局部图,地面标高+50 m,水位面为+50 m,底边界标高-140 m,矿体由下向上开采,采矿方法为胶结充填法.矿层走向长50 m,倾斜方向长80 m,平均厚度为20 m.矿区地表是第4系含水层,下面分别是砂砾岩含水层和主岩枝花岗斑岩,矿层与砂砾岩含水层直接接触.其中矿体为弱透水层,花岗斑岩充当隔水层.
|
| 图 1 矿区17A号勘探线剖面图 Figure 1 Prospecting line 17A profile map in mining area |
表 1为矿区现场试验测得的各岩体参数.由于计算模型是从实际地质体中取出的一部分,其边界处依然要受到力或位移的约束.在FLAC3D中,模型中的位移约束主要通过固定模型边界处节点的速度来实现,应力边界则是用来模拟模型边界处节点的应力.根据实际情况,在该项目中用FIX命令来施加模型的约束条件.模型前后和左右边界施加水平约束,即侧面边界水平位移为0;模型底部边界固定,即底部边界水平、垂直位移均为0;模型顶部为地表,看作是自由面,无任何约束.模型四周给定不透水边界,并在模型上施加初始孔隙水压力.
| 岩体 | 矿体 | 第4系 | 砂砾岩 | 花岗斑岩 | 充填体 |
| 弹性模量/MPa | 16 498 | 200 | 9 264 | 5 949 | 500 |
| 泊松比 | 0.2 | 0.3 | 0.25 | 0.2 | 0.3 |
| 内摩擦角 | 40.7 | 25 | 35.54 | 31.64 | 26 |
| 黏聚力/MPa | 4.949 | 0.2 | 3.606 | 2.799 | 0.1 |
| 抗拉强度/MPa | 2.5 | 0.2 | 1.8 | 0.9 | 0.2 |
| 密度/(t·m-3) | 3.3 | 1.8 | 2.68 | 2.57 | 1.4 |
| 渗透系数/(m2/(Pa·s-1)-1) | 3×10-11 | 8×10-10 | 2×10-11 | 1×10-12 | 5×10-10 |
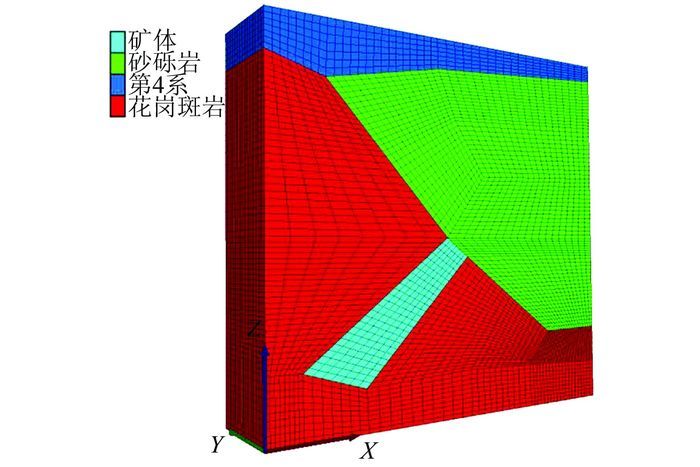
根据17A号勘探线剖面图,用FLAC3D建立的三维模型见图 2.模型的尺寸大小为200 m×50 m×190 m,一共划分为63 400个单元体.整个模型包含有4种材料,分别是第4系含水层、砂砾岩含水层、主岩枝花岗斑岩以及矿体.
|
| 图 2 FLAC3D计算模型 Figure 2 Calculation model in FLAC3D |
岩土强度理论是岩土理论的重要组成部分,一直是众多学者研究的热点.大量的试验和工程实践已证实,Mohr-Coulomb强度理论能较好地描述岩土材料的强度特性和破坏行为,在岩土工程领域得到了广泛的应用[12].因此,本文选择FLAC3D中的Mohr-Coloumb强度理论模型作为本构模型.
2.4 数值模拟结果分析1) 初始孔隙水压力分布特征
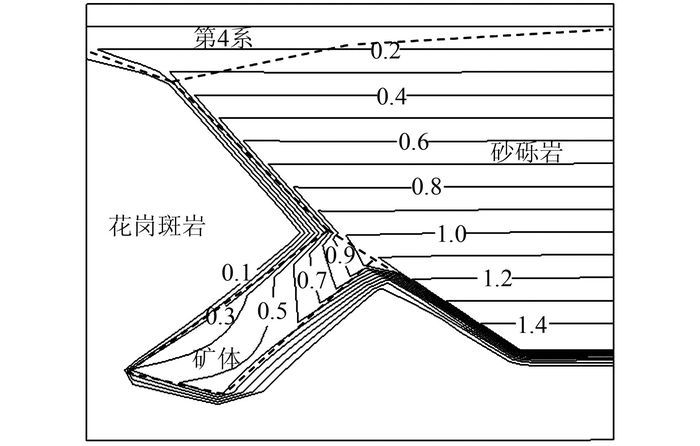
在矿体开采前,首先模拟研究区域的初始耦合渗流场,得到初始孔压等值线图(见图 3).从初始孔压云图可以看出,在第4系和砂砾岩两个含水层中的孔隙水压力等值线呈水平分布,这是因为渗流场达到平衡,孔隙水压力可以看作是静水压力;矿体是弱透水层,离含水层的距离越远孔隙水越难渗透,因而孔隙水压力越小;主岩枝花岗斑岩透水性很小,完全充当隔水层的作用,所以孔隙水压力基本为0.
|
| 图 3 初始孔压等值线图(单位:MPa) Figure 3 Contour map of initial pore pressure (unit:MPa) |
2) 渗流速度矢量分析
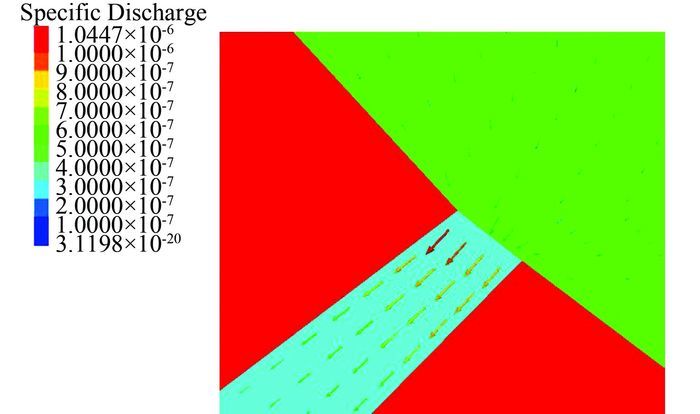
图 4为初始渗流速度矢量局部图.可以看出隔水层中的渗流速度基本为0,含水层中的渗流速度较小,越靠近砂砾岩的矿体,其渗流速度越大,渗流速度最大的地方是与砂砾岩接触的那部分矿体,这是因为矿体与砂砾岩交界处渗透坡降比较大.这说明了越靠近砂砾岩含水层,矿体突水的危险性就会越大.
|
| 图 4 渗流速度矢量局部图(单位:m/s) Figure 4 Vectograph of seepage velocity (unit:m/s) |
3) 涌水量计算
矿体的开采相当于力学边界条件发生改变,对耦合场造成扰动,需要重新进行流固耦合计算.通过模拟开采工作面的推进,即矿体的开采(由下向上开采),拟对开采过程中的7个工作面进行涌水量计算.
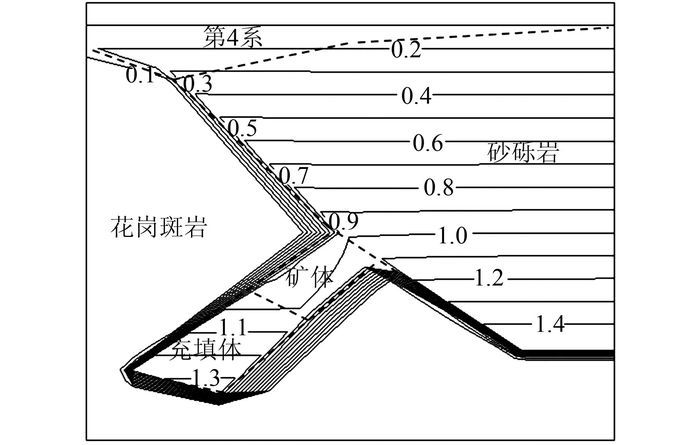
图 5是工作面推进到与含水层距离为35 m时的孔压等值线图.由于矿体的回采与充填,渗流场被扰动.充填体的渗透系数比矿体小,造成回采充填区的孔压比矿体的孔压大,会加速水体从含水层向矿体的渗透.从图 4、5看出,工作面前方的矿体孔压变大,大于初始渗流场同一位置的孔压约0.4 MPa,工作面比开采前更容易发生突水.
|
| 图 5 工作面距离含水层35 m时的孔压等值线图(单位:MPa) Figure 5 Pore pressure contour map when working face and aquifer is 35 m apart (unit:MPa) |
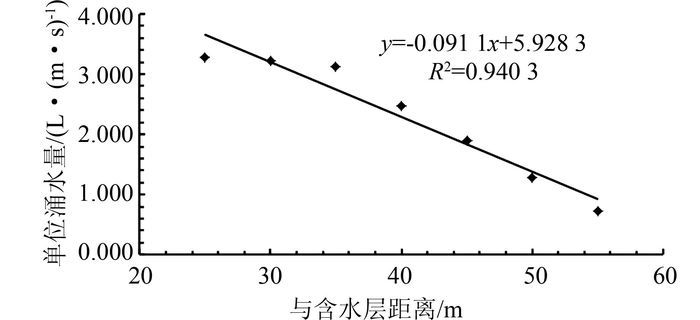
FLAC3D通过计算开采区域断面节点的不平衡水头,实现对工作面涌水量的预计.这需要利用FLAC3D软件中内置的FISH语言,编写并调用相关函数,计算出开采过程中7个工作面的涌水量.以工作面与含水层距离为x轴,单位涌水量为y轴,将得到的结果进行线性拟合,见图 6.
|
| 图 6 单位涌水量曲线图 Figure 6 Specific water inflow curve |
从图 6可以看出,随着工作面的推进,即矿体的开采范围增大,与含水层的距离越来越小,工作面的涌水量随之增大.由于工作面的推进,使渗流场发生扰动,工作面前方的矿体进一步充水,更加增大了工作面突水的危险,这和前面的渗流速度矢量图表明的结果一致.经现场钻孔(ZK1712) 抽水试验,径流排泄区单位涌水量达2.975 L/(m·s).当工作面与含水层的距离为35 m时,单位涌水量为3.124 L/(m·s),大于排水量2.975 L/(m·s),工作面会有突水的危险;当工作面与含水层的距离≥40 m时,单位涌水量小于排水量,不会发生突水.
因此,为了防止工作面突水,必须保留一部分的矿体作为防水矿柱,由上可知须保持工作面与含水层的距离不少于40 m,才使得工作面单位涌水量不超过排水量,因而防水矿柱才能发挥效果.
4) 塑性区分析
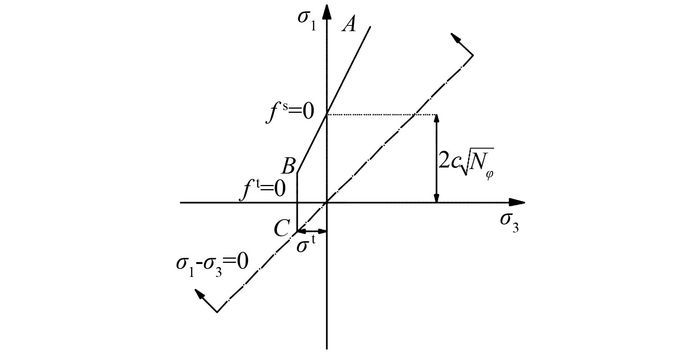
在FLAC3D中,对Mohr-Coulomb强度准则在主应力平面中(σ3, σ1)进行了描述,如图 7所示.为了方便说明,图中的主应力以压应力为正,拉应力为负.
|
| 图 7 Mohr-Coulomb强度准则(主应力平面中) Figure 7 Mohr-Coulomb failure criterion(principal stresses planes) |
图 7中,A点到B点的剪切屈服函数为
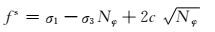 (5)
(5)
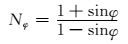 (6)
(6)
B点到C点的拉屈服函数为
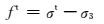 (7)
(7)
式中:φ为内摩擦角;c为黏聚力;σt为抗拉强度.
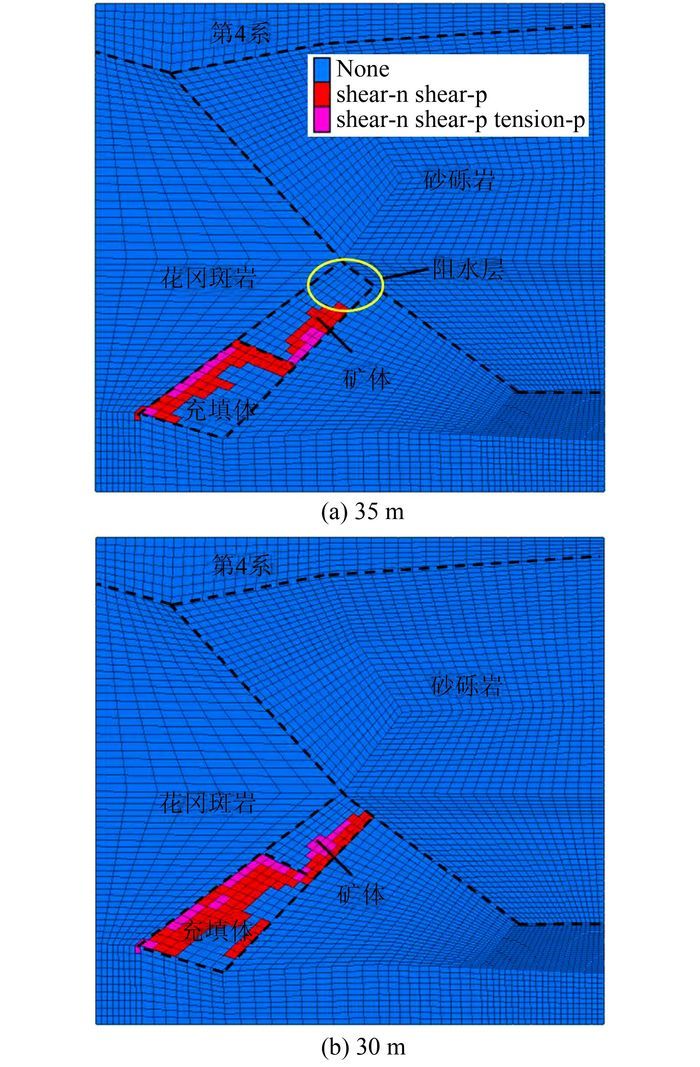
矿体回采充填后,在耦合的应力场和渗流场条件下,工作面与含水层距离35 m和30 m时产生的塑性区分布分别如图 8(a)、(b)所示.随着矿体地不断开采与充填,应力重分布后,上覆岩层由矿柱与充填体共同支撑;充填体强度与矿体相比较低,故矿柱起主要支撑作用,会使工作面前方的矿柱形成应力集中.在此期间,渗流场经过扰动后再次达到稳定,使工作面前方的矿柱孔压变大,有效应力降低,更容易产生塑性区,有利于塑性区的进一步延伸扩展.而塑性区隔水能力会降低,不能起到防水矿柱的作用.刘波[13]和施龙青[14]都认为塑性区渗透系数会变大,最终会形成导水裂隙带;Zhu[15]研究表明采矿产生的损伤屈服区会成为渗水通道,引起突水事故的发生.
|
| 图 8 工作面距离含水层35 m和30 m时的塑性区分布 Figure 8 Failure zone distribution while the working face and the aquifer is 35m and 30m apart |
从图 8(a)看出,由于工作面离含水层有足够的距离,存在着阻水层,因而导水裂隙带没有与含水层连通,顶板不会发生突水;图 8(b)中,工作面离含水层没有足够的安全距离,导水裂隙带的范围已经波及到上覆含水层,将有突水的危险.由上所述,为避免导水裂隙带与含水层贯通,防水矿柱的高度应该取35 m.
使用胶结充填法开采矿体时,由于充填接顶率小,充填体沉缩产生的残余空间会使顶板围岩发生变形破坏[16].金属矿地质条件复杂且各矿差异大, 目前没有成熟的冒落带高度和导水裂隙带高度计算经验公式;而我国在水体下采煤开展了大量的研究和实践,积累了可靠的计算导高的经验公式[17].因此,选用煤炭系统流行的经验公式进行计算.依据《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》[18],防水矿柱的高度按下式计算:
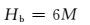 (10)
(10)
式中:Hsh为防水矿柱高度;Hli为导水裂隙带高度;Hb为保护层厚度;M为充填未结顶高度,胶结充填采矿法中,取最大未结顶高度2 m[19].
由式(8)~(10) 计算可得防水矿柱高度为
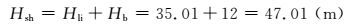
而采用FLAC3D模拟计算推求得到的防水矿柱高度为35 m,表明上述经验公式计算得出的结果偏安全,有些保守.经验公式不仅验证了数值模拟结果的合理性,也说明了FLAC3D能够进一步优化防水矿柱留设的尺寸.
3 结论为了避免开采水下矿体时,出现回采充填区工作面突水问题,本文探索在渗流场和应力场耦合的作用下,如何从涌水量和塑性区的计算来研究留设防水安全矿柱,得出了以下结论:
1) 涌水量计算是从耦合计算得出的渗流场方面来考虑,用渗流矢量图定性地描述矿体越靠近含水层,渗流速度越大;计算7个工作面的单位涌水量,定量地分析了随着与含水层距离越来越小,涌水量越来越大.经计算,防水矿柱高度取为40 m,工作面涌水量小于排水量,不会发生突水.
2) 塑性区分析是从耦合计算得出的应力场方面来考虑,矿体的回采使工作面前方的矿柱产生应力集中,以及增大矿柱孔压,降低其有效应力,形成塑性区即导水裂隙带.随着工作面的不断推进,导水裂隙带会向前延伸,最终会波及到含水层.经模拟,防水矿柱高度取为35 m,导水裂隙带不会与含水层贯通,不会有突水的危险.
3) 综合考虑涌水量和塑性区(导水裂隙带)两个方面的影响,防水矿柱的高度取为40 m,说明了经验公式算得的47 m相对保守,数值模拟结果提高了矿体利用率.这里需要说明的是:采用塑性区来代替导水裂隙带是一种近似处理方法,更加准确的方法将在后期的工作中研究.
| [1] |
张金才.
岩体渗流与煤层底板突水[M]. 北京: 地质出版社, 1997.
Zhang Jincai. Rock Seepage and Water Projecting in Coal Bed[M]. Beijing: Geological Publishing House, 1997. |
| [2] |
姚金蕊, 李夕兵, 周子龙. "三下"矿体开采研究[J].
地下空间与工程学报, 2005, 1(S1): 1073–1075.
Yao Jinrui, Li Xibing, Zhou Zilong. Study of excavation for the under-three-objects ore body[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(S1): 1073–1075. |
| [3] |
黄建鑫. 水银洞金矿水下矿体的开采[J].
现代矿业, 2012(1): 74–75.
Huang Jianxin. Excavation of Shuiyindong gold deposit under the water[J]. Modern Mining, 2012(1): 74–75. |
| [4] |
曹秋菊, 王金安, 纪洪广. 不整合地层下开采防水煤柱合理宽度的研究[J].
中国矿业, 2012, 21(3): 66–69.
Cao Qiuju, Wang Jinan, Ji Hongguang. Research on reasonable width of waterproof coal pillar when mining under the unconformity strata[J]. China Mining Magazine, 2012, 21(3): 66–69. |
| [5] |
张林山, 秦靖宇. 小煤窑采空区留设防水煤柱合理宽度的探讨[J].
华北科技学院学报, 2009, 6(4): 66–69.
Zhang Linshan, Qin Jingyu. The discussion about waterproof mine columniation pillar width in small coal mines bare area[J]. Journal of North China Institute of Science and Technology, 2009, 6(4): 66–69. |
| [6] |
王大设, 王俊, 姚多喜. 孙疃煤矿102采区防水煤岩柱留设技术研究[J].
中国煤炭地质, 2011, 23(3): 34–38.
Wang Dashe, Wang Jun, Yao Duoxi. Study on reasonable water barrier leaving key technologies in No.102 minning district, Suntuan coalmine[J]. Coal Geology of China, 2011, 23(3): 34–38. |
| [7] |
杨本水, 王从书, 阎昌银. 中等含水层下留设防砂煤柱开采的试验与研究[J].
煤炭学报, 2004, 27(4): 342–346.
Yang Benshui, Wang Congshu, Yan Changyin. Study and trial on explitation of retaining safety coal pillar against sand under medium-thickness aquifer layer[J]. Journal of China Coal Society, 2004, 27(4): 342–346. |
| [8] |
孟召平, 高延法, 卢爱红, 等. 第四系松散含水层下煤层开采突水危险性及防水煤柱确定方法[J].
采矿与安全工程学报, 2013, 30(1): 23–29.
Meng Zhaoping, Gao Yanfa, Lu Aihong, et al. Water inrush risk evaluation of coal mining under Quaternary alluvial water and reasonable design method of waterproof coal pillar[J]. Journal of Mining and Safety Engineering, 2013, 30(1): 23–29. |
| [9] |
尹尚先. 陷落柱防水煤柱留设对围岩变形影响的数值模拟[J].
煤炭学报, 2006, 31(2): 179–182.
Yin Shangxian. Numerical simulation of influence of water barrier pillars for subsided column on rock failure in mining process[J]. Journal of China Coal Society, 2006, 31(2): 179–182. |
| [10] |
王涛, 韩煊, 赵先宇, 等.
FLAC3D数值模拟方法及工程应用——深入剖析FLAC3D5.0[M]. 北京: 中国建筑工业出版社, 2015.
Wang Tao, Han Xuan, Zhao Xianyu, et al. FLAC3D Numerical Simulation Method and Engineering Application—Deeply Analyze FLAC3D 5.0[M]. Beijing: China Architecture & Building Press, 2015. |
| [11] | Itasca Consulting Group Inc. FLAC3D-Fast Lagrangian Analysis of Continua in 3 Dimensions[Z]. Ver. 3.0 User's Manual. ICG, Minneapolis, 2005. |
| [12] |
贾善坡, 陈卫忠, 杨建平, 等. 基于修正Mohr-Coulomb准则的弹塑性本构模型及其数值实施[J].
岩土力学, 2010, 31(7): 2051–2058.
Jia Shanpo, Chen Weizhong, Yang Jianping, et al. An elastoplastic constitutive model based on modified Mohr-Coulomb criterion and its numerical implementation[J]. Rock and Soil Mechanics, 2010, 31(7): 2051–2058. |
| [13] |
刘波, 贺雷, 罗立平. 流-固耦合作用下防隔水煤柱留设的数值模拟[J].
采矿与安全工程学报, 2010, 26(4): 445–449.
Liu Bo, He Lei, Luo Liping. Numerical modeling on fluid-solid coupling for the waterproof coal pillar design[J]. Journal of Mining and Safety Engineering, 2010, 26(4): 445–449. |
| [14] |
施龙青, 韩进, 刘同彬, 等. 采场底板断层防水煤柱留设研究[J].
岩石力学与工程学报, 2005(S2): 5585–5590.
Shi Longqing, Han Jin, Liu Tongbin, et al. Study on design of safety pillar against water-inrush through stope sill faults[J]. Chinese Journal of Rock Mechanics and Engineering, 2005(S2): 5585–5590. |
| [15] | Zhu W C, Wei C H. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model[J]. Environmental Earth Sciences, 2011, 62(1): 43–54. DOI:10.1007/s12665-010-0494-6 |
| [16] | Xia Yucheng, Zhi Jianfeng, Sun Xueyang. Study on relation between tectonic stress and coal-mining subsidence with similar material simulation[J]. Journal of Coal Science & Engineering, 2005(2): 37–40. |
| [17] |
吴浩, 赵国彦, 马少维, 等. 滨海基岩矿床开采防水矿岩柱高度的确定[J].
中国地质灾害与防治学报, 2014, 25(1): 44–50.
Wu Hao, Zhao Guoyan, Ma Shaowei, et al. Design on the size of waterproof pillar (rock) in subsea bedrock mining[J]. The Chinese Journal of Geological Hazard and Control, 2014, 25(1): 44–50. |
| [18] |
国家煤炭工业局. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S]. 北京: 煤炭工业出版社, 2000
National Coal Industry Bureau. Coal Pillar Designing and Mining Regulations of Buildings, Water, Railway and Main Roadway [S]. Beijing: China Coal Industry Publishing Home, 2004. |
| [19] |
赵彬, 王新民, 李耀武, 等. 康家湾永久防水矿柱安全开采可行性[J].
昆明理工大学学报(理工版), 2009, 34(1): 27–34.
Zhao Bin, Wang Xinmin, Li Yaowu, et al. Safe mining feasibility of permanent waterproof jamb in Kang jiawan mine[J]. Journal of Kunming University of Science and Technology (Science and Technology), 2009, 34(1): 27–34. |
 2017, Vol. 50
2017, Vol. 50




