武汉大学学报(工学版)   2016, Vol. 49 Issue (5): 654-660

文章信息

康飞, 李俊杰, 李守巨, 李红军
KANG Fei, LI Junjie, LI Shouju, LI Hongjun
边坡系统可靠度分析智能响应面法框架
Framework of intelligent response surface methods for system reliability analysis of slopes
武汉大学学报(工学版), 2016, 49(5): 654-660
Engineering Journal of Wuhan University, 2016, 49(5): 654-660
http://dx.doi.org/10.14188/j.1671-8844.2016-05-003

文章历史

收稿日期: 2016-03-25
 Abstract              PDF               Figures               Tables
引用本文 0
康飞, 李俊杰, 李守巨, 李红军. 边坡系统可靠度分析智能响应面法框架[J]. 武汉大学学报(工学版), 2016, 49(5): 654-660.
KANG Fei, LI Junjie, LI Shouju, LI Hongjun. Framework of intelligent response surface methods for system reliability analysis of slopes[J]. Engineering Journal of Wuhan University, 2016, 49(5): 654-660.
边坡系统可靠度分析智能响应面法框架
康飞1, 李俊杰1, 李守巨2, 李红军3     
1. 大连理工大学水利工程学院，辽宁 大连 116024;
 2. 大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116024;
 3. 中国水利水电科学研究院, 北京 100048
收稿日期: 2016-03-25
作者简介: 康飞（1982-），男，副教授，主要从事水工结构安全监测与数值分析研究，E-mail: kangfei@dlut.edu.cn.
通讯作者: 李俊杰（1963-），男，教授，博士生导师，主要从事水工建筑物安全监测与数值分析研究，E-mail: lijunjie@dlut.edu.cn
基金项目: 国家重点研发计划资助项目（编号：2016YFC0401600）; 国家自然科学基金项目(编号：51109028);工业装备结构分析国家重点实验室开放基金(编号：GZ15207);中央高校基本科研业务费专项资金资助项目(编号：DUT15LK11);中国水科院科研专项青年专项（编号：GE0145B112016）.
摘要: 多失效模式情况下，边坡体系可靠性分析较为复杂.提出了基于计算机试验结合机器学习理论建立边坡系统（体系）可靠度分析智能响应面法的一般框架.边坡体系可靠性分析智能响应面法步骤包括：样本生成、模型参数优化、智能响应面建立、蒙特卡罗模拟计算失效概率.对支持向量机、高斯过程等多种智能机器学习理论用于建立智能响应面的性能进行了对比分析.通过典型边坡的体系可靠度分析，验证了小样本情况下智能响应面法在边坡体系可靠性分析中的可行性和优越性.
关键词： 边坡稳定     系统可靠性     响应面法     人工蜂群算法     高斯过程     支持向量机     最小二乘支持向量机    
Framework of intelligent response surface methods for system reliability analysis of slopes
KANG Fei1, LI Junjie1, LI Shouju2, LI Hongjun3     
1. School of Hydraulic Engineering, Dalian University of Technology, Dalian 116024, China;
 2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China;
 3. China Institute of Water Resources and Hydropower Research, Beijing 100048, China
Abstract: System reliability analysis of soil slopes is a quite complex task under the multiple failure modes situation. This study proposes a general framework of intelligent response surface methods, which combine computer experimental methods with machine learning theories, for slope system reliability analysis. The main steps of the proposed method include, samples generation, model parameters optimization, intelligent response surface establishment and Monte Carlo simulation for calculating the failure probability. Performance of several intelligent response surfaces established by support vector machines (SVM) and Gaussian process regression are compared. The proposed methods are tested on three typical slope examples with obvious system effect. The results show that the intelligent response surface methods with small samples are effective for slope system reliability analysis.
Key words: slope stability     system reliability     response surface     artificial bee colony algorithm     Gaussian processes     support vector machines(SVM)     least squares    

滑坡灾害会带来严重的生命、财产损失和环境破坏.可靠度分析是考虑土体参数不确定性对边坡稳定性影响的有效工具.常用的边坡可靠度分析方法，如一次二阶矩法通常计算对应某一最危险滑动面的可靠度[1]，该方法对于空间土性较为均匀、潜在失效模式较为单一(失效模式间相关性较强)的边坡是有效的，但对于不同滑动面安全系数相关性不强的情况，该方法得到的失效概率将会小于所有可能滑动面的失效概率.因此，为充分考虑边坡系统具有的多种潜在失效模式，有必要采用系统可靠度分析的思路求解边坡整体可靠度问题，以期得到更为准确的可靠度水平.

边坡系统(体系)可靠度分析研究近年来得到越来越多的重视.Oka和Wu[2],Chowdhury和Xu[3],Low等[4]采用了可靠度界限法，该方法能够计算系统失效概率可能范围的上下界.一些能够直接计算失效概率的方法也被提出来，如蒙特卡罗有限元法[5]、重要性抽样法[6]、子集模拟法[7]等.随后又提出了基于代表性滑动面的分析方法[8-10]，该方法通过在大量可能的滑动面中识别出代表性滑动面来计算边坡的体系可靠度.但目前在如何识别代表性滑动面及代表性滑动面的数目等方面还需要深入研究.蒙特卡罗法(Monte Carlo simulation,MCS)是计算系统失效概率最直接的方法，但其计算效率较低，特别是当确定性分析采用非线性有限元等耗时较长的程序时.响应面法[11](response surface method,RSM)是一种改进MCS效率的有效方法，已被较多地用于边坡可靠度分析问题[12,13]，但研究对象多为失效模式间相关性较强的边坡.对具有明显系统效应的边坡，还需要深入研究如何建立有效的响应面.

传统的多项式响应面不能准确地逼近边坡系统可靠度分析中非线性程度较强的极限状态方程[14]，因此有必要引入具有更大灵活性和更强非线性学习能力的智能机器学习理论来建立智能响应面[15-17].在已有研究成果的基础上，提出了基于智能优化结合机器学习数学模型建立边坡系统可靠度分析智能响应面的一般框架.比较了支持向量回归[16](support vector regression,SVR)、ν-支持向量机[17](ν-support vector machine,ν-SVM)、最小二乘支持向量机[18](least squares SVM,LSSVM)、高斯过程回归[15](Gaussian process regression，GPR)等多种智能响应面的性能，结合计算机试验方法，探讨了小样本智能响应面计算边坡系统可靠度的可行性.研究结果对促进边坡体系可靠性分析方法的发展、提高分析效率具有重要意义.

1 边坡体系可靠性分析

边坡概率稳定性分析能够反映出非确定参数对于边坡稳定性的影响，非确定参数构成的向量可表达为x = [x1, x2, …, xD]，D为非确定性参数的个数，边坡的失稳概率Pf可以表达为如下的积分形式[12]

${{P}_{f}}=P\{g(x)\le 0\}=\int_{g(x)\le 0}{{{f}_{x}}}(x)dx$    (1)

式中：g(x)为功能函数；fx(x)为联合概率密度函数.

功能函数一般定义为

$Z=g(x)={{F}_{s}}(x)-1.0$    (2)

式中，Fs为用确定性边坡稳定分析方法求解得到的安全系数.

要直接根据式(1)计算边坡的失稳概率较为困难，因此提出了一次二阶矩法、蒙特卡罗法等近似求解方法.一次二阶矩法被较多地应用于求解边坡可靠度分析问题，该方法只能够得到概率最危险滑动面的失稳概率，往往小于整个边坡系统所有可能滑动面的失稳概率.从系统可靠度分析角度看，边坡系统可以看作一个串联系统，系统失稳概率可以表达为[8]

${{P}_{f}}\approx P(E({{S}_{1}})\cup E({{S}_{2}})\cup \cdots \cup E({{S}_{M}}))$    (3)

式中：P(·) 为失稳事件发生概率；E(Si) 代表沿滑动面Si发生失稳破坏；M为计算考虑的滑动面个数.尽管理论上边坡失稳滑动面有无穷多个，但不同滑动面的安全系数之间存在高度的相关性，因此系统失效概率常由有限个代表性滑动面所确定.通常沿各滑动面的失稳破坏既不会是统计独立的也不会完全相关，因此失稳概率会处于两个极值之间，如下式[16]：

$\underset{i\in 1,M}{\mathop{\max }}\,{{P}_{fi}}\le {{P}_{f}}\le 1-\prod\limits_{i=1}^{M}{(1-{{P}_{fi}})}$    (4)

式中：Pfi为沿Si的失稳概率；M为计算考虑的滑动面数.

基于代表性滑动面的分析方法目前处于发展之中，其关键问题是如何确定代表性滑动面及代表性滑动面数目.另一种有效方法为蒙特卡罗法，采用该方法时失稳概率可计算为 Pf=Nf/Ns ，其中Ns为抽样模拟总次数，Nf为失稳破坏发生次数.MCS较为直接，但需要大量的确定性分析计算，耗时较长.为提高计算效率，提出如下小样本智能响应面法.

2 小样本智能响应面法 2.1 响应面法数学模型

在传统响应面法中，真实的目标函数采用二次多项式近似为[14]

$g(x)={{b}_{0}}+\sum\limits_{i=1}^{D}{{{b}_{i}}{{x}_{i}}}+\sum\limits_{i=1}^{D}{{{b}_{D+i}}x_{i}^{2}}$    (5)

式中：D为非确定参数个数；bi为多项式系数.相对于传统响应面法，智能响应面采用非线性拟合能力更强的机器学习数学模型来建立响应面.

1) 支持向量机

支持向量机[16,17]是数据挖掘中的一项新技术，它基于统计学习理论，采用该技术实现由低维空间到高维空间的非线性映射，成功解决了“维数灾难”问题，其采用的结构风险最小化原则可避免神经网络的“过学习”现象，既具有严格的理论基础，又能较好解决小样本、非线性、高维数等实际问题.通过引入结构风险最小化准则和ε不敏感损失函数，可建立支持向量机的优化原问题，引入拉格朗日乘子后其对偶问题为

$\begin{align} & \max R({{\alpha }_{i}},\alpha _{i}^{*})=-\frac{1}{2}\sum\limits_{i,j=1}^{l}{({{\alpha }_{i}}-\alpha _{i}^{*})({{\alpha }_{j}}-\alpha _{j}^{*})K({{x}_{i}},{{x}_{j}})} \\ & -\varepsilon \sum\limits_{i=1}^{l}{({{\alpha }_{i}}+\alpha _{i}^{*})+}\sum\limits_{i=1}^{l}{{{y}_{i}}({{\alpha }_{i}}-\alpha _{i}^{*})} \\ \end{align}$    (6)
$\text{St}\text{.}\sum\limits_{i=1}^{l}{({{\alpha }_{i}}-\alpha _{i}^{*})}=0,\text{ 0}\le {{\alpha }_{i}},\alpha _{i}^{*}\le C$    (7)

式中：αi,αi*为拉格朗日乘子；K(xi,xj)为核函数，常用的是径向基核函数：

$K({{x}_{i}},{{x}_{j}})=\exp (-\gamma {{\left\| {{x}_{i}}-{{x}_{j}} \right\|}^{2}})$    (8)

式中：γ 为核函数参数.求解上述优化问题，可得到SVR预测方程：

$f(x)=\sum\limits_{i=1}^{l}{({{\alpha }_{i}}-\alpha _{i}^{*})}K({{x}_{i}},x)+b$    (9)

式中：b为预测方程常数项.模型求解过程中需要输入的参数为C、ε 和γ，由于参数ε的范围不易确定，因此研究者又提出了ν-SVM模型，即引入参数ν∈(0,1］，让程序自动计算参数ε的值，支持向量的个数由参数ν确定.

Suykens等[18]采用等式最小二乘误差方程代替SVM模型中的不等式约束方程，提出了LSSVM模型，大幅度提高了SVM的建模效率.

2) 高斯过程回归

在机器学习领域，高斯过程[15](Gaussian processes,GPs)是指在高斯随机过程与贝叶斯学习理论基础上发展起来的一种机器学习方法.GPs被认为是处理回归、分类、降维等问题最先进的贝叶斯机器学习工具.和神经网络、SVM相比，GPs有其自身的一些优势，如超参数可以通过最大似然估计快速优化求解；输出具有明确的概率意义，提供了对预测结果不确定程度的估计.

高斯过程回归预测均值和方差为

${{{\bar{f}}}_{*}}=K({{X}_{*}},X){{[K(X,X)+\sigma _{n}^{2}I]}^{-1}}y$    (10)
$\operatorname{cov}({{f}_{*}})=K({{X}_{*}},{{X}_{*}})-K({{X}_{*}},X){{[K(X,X)+\sigma _{n}^{2}I]}^{-1}}K(X,{{X}_{*}})$    (11)

式中：K[X,X]为协方差矩阵，其元素为Kij=k(xi,xj)，体现了xi,xj的相关性.常用的协方差函数为

$\begin{align} & k({{x}_{p}},{{x}_{q}})=\sigma _{n}^{2}\delta (p,q)+\sigma _{f}^{2}\exp (-\frac{1}{2}{{({{x}_{p}}-{{x}_{q}})}^{\text{T}}}M({{x}_{p}}-{{x}_{q}})) \\ & =\sigma _{f}^{2}\exp (-\frac{1}{2}\sum\limits_{i=1}^{D}{\frac{{{({{x}_{p,i}}-{{x}_{q,i}})}^{2}}}{l_{i}^{2}}})+\sigma _{n}^{2}\delta (p,q) \\ \end{align}$    (12)

式中：M=diag(l)-2,l=[l1,l2,…，lD]T.θ=(lnl1,…,lnlD,lnσf,lnσn)为超参数，可采用共轭梯度法求解.

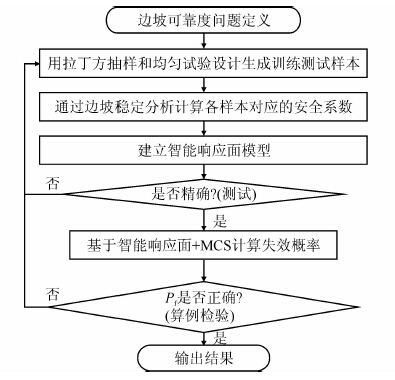
2.2 小样本智能响应面法一般框架

小样本智能响应面法主要思路是利用试验设计方法生成能够均匀覆盖变量区间的试验样本，以减少需要的样本个数.采用具有较强非线性拟合能力的智能机器学习模型建立响应面，最后用智能响应面代替确定性边坡稳定分析，预测边坡安全系数，基于蒙特卡罗法抽样计算系统失稳概率.边坡系统可靠度分析小样本智能响应面法一般框架可用图 1表示.关于建模样本个数N，对边坡系统可靠度分析问题的研究表明，N=15D可以得到较好的结果[15-17].

图 1 边坡体系可靠度分析小样本智能响应面法一般框架 Figure 1 Framework of intelligent RSM for system reliability analysis of slopes
图选项
2.3 模型参数优化

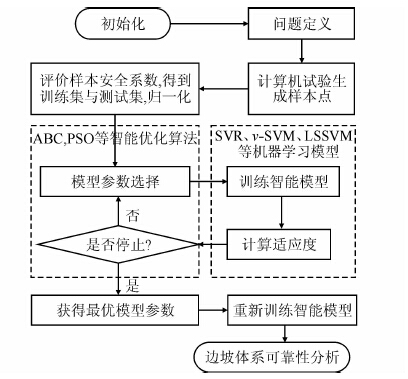
在SVM、ν-SVM、LSSVM模型中都有需要用户输入的模型参数，参数的选择对模型预测性能的影响较大.为此采用群体智能优化算法[15-17]，如粒子群算法(particle swarm optimization,PSO)、人工蜂群算法(artificial bee colony algorithm,ABC)等对模型参数进行优化，优化过程以交叉验证法得到的均方误差(mean square error,MSE)作为优化目标函数.群体智能优化智能响应面法流程见图 2.

图 2 与群体智能优化相结合的智能响应面法一般框架 Figure 2 Framework of intelligent RSM combined with swarm intelligence optimization
图选项
3 算例分析

对各测试算例，采用拉丁方抽样生成建模样本.对于对数正态分布参数，样本点生成区间为(μx - 3σx，μx + 3σx)；对于正态分布参数，样本点生成区间为(μx - 4σx，μx + 4σx)[16](μx、σx分别为参数的均值和标准差).建模样本个数取为N=15D[16]，基于均匀试验设计生成测试样本，测试样本个数取为20[15-17].文献[16, 17]比较了网格搜索、PSO和ABC优化支持向量机模型的性能，结果表明PSO和ABC都具有较强的全局优化能力，搜索精度相近，效率优于网格搜索法，本文选用ABC，基于5-fold交叉验证法进行模型参数优化.在ABC算法中群体规模设置为NP=20，最大迭代次数为100，控制limit=(NP/2)×D，为考察结果稳定性，每个优化问题运行20次.LSSVM参数搜索区间设置为

log10C∈[2,-6],log102γ∈[2-,3]

SVR模型参数搜索区间为

$\eqalign{ & {\log _{10}}C \in \left[ {0,4} \right] \cr & {\log _{10}}\gamma \in \left[ { - 2,2} \right] \cr & {\log _{10}}\varepsilon \in \left[ { - 4,0} \right] \cr} $

ν-SVM参数搜索区间为[16,17]

$\eqalign{ & {\log _{10}}C \in \left[ { - 1,2.5} \right] \cr & {\log _{10}}\gamma \in \left[ { - 1,1} \right] \cr & {\log _{10}}\varepsilon \in \left[ {0.2,0.8} \right] \cr} $
3.1 黏性土坡

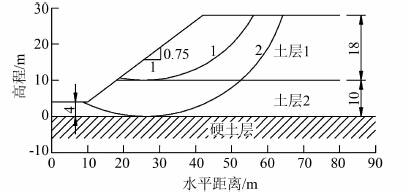
该算例为一两层黏性土坡[6]，边坡剖面如图 3所示，材料参数见表 1.由于摩擦角φu=0，剪切强度主要由黏聚力cu确定，简化Bishop法和瑞典圆弧法会得到相同的安全系数.基于材料参数均值计算的安全系数为1.993，与Cho[10]计算得到的1.992一致.图 4中同时给出了Low等[4]识别出的两个代表性滑动面.

图 3 算例1黏性土坡剖面 Figure 3 Cross-section of the slope consisted by two clay layers
图选项
表 1 算例1材料参数及其统计特性 Table 1 Statistical properties of soil parameters in Example 1
土层编号 容重γ/(kN·m-3) 不排水剪强度 cu/kPa
均值 COV 分布
1 19.0 120 0.3 对数正态
2 19.0 160 0.3 对数正态
表选项

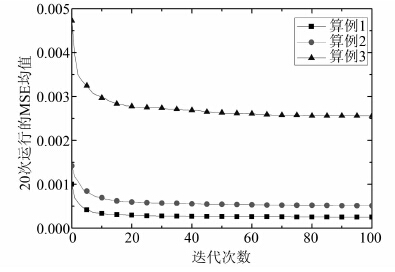
本例中训练样本个数为N=15D=30.采用ABC分别优化3种支持向量机模型参数，优化结果见表 2，ABC优化LSSVM的误差均值变化过程如图 4所示.

图 4 ABC优化LSSVM模型参数收敛过程曲线 Figure 4 Convergence processes of ABC for optimizing LSSVM models
图选项
表 2 支持向量机模型参数 Table 2 Parameters of support vector machine models
算例号 SVR模型参数[C,γ,ε] ν-SVM模型参数[C,γ,ν] LSSVM模型 参数[C,2γ]
1 [100.46,0.968 4,0.006 3] [66.156,1.140 2,0.519 7] [4 674.5,0.443]
2 [13.08,2.029 0,0.005 8] [9.621 6,2.016 2,0.206 5] [1 223.9,0.296]
3 [105.84,0.238 7,0.002 2] [86.955,0.250 1,0.652 9] [3.65e4,4.503]
表选项

采用不同可靠度分析方法得到的失稳概率比较如表 3所示.可以看出蒙特卡罗法得到的失稳概率约为0.40%，FORM和传统响应面法都严重低估了失稳概率值.所提出的智能响应面法所得失稳概率与直接MCS法及其他系统可靠度分析方法计算结果接近，尤以GPR、SVR和ν-SVM计算结果较好.

表 3 算例1不同方法可靠度分析结果 Table 3 Results of probabilistic analysis for example 1
分析方法 失稳概率Pf/% 参考文献
FORM 0.16 [6]
重要性抽样1 000次 0.41(COV=6.6%) [6]
MCS(分层RSM) 0.390 [19]
MCS抽样2万次 0.405 [19]
MCS(传统RSM) 0.170(COV=7.7%) [14]
MCS(Kriging) 0.458(COV=4.7%) [14]
MCS抽样2万次 0.415 [10]
MCS(GPR) 0.384(COV=1.6%) [15]
MCS(SVR) 0.397(COV=1.6%) [16]
MCS(ν-SVM) 0.405(COV=1.6%) [17]
MCS(LSSVM) 0.356(COV=1.6%) 本文
注：分析方法一栏括号内为响应面模型，GPR、SVR、ν-SVM、LSSVM抽样次数为106次.
表选项
3.2 路堤边坡

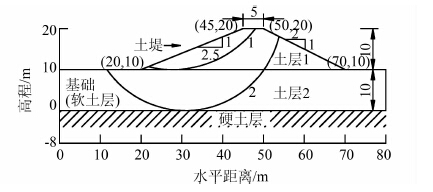
算例2为一软土层上的路堤边坡[3]，边坡剖面见图 5，图中同时给出了两个代表性滑动面[19]，材料参数见表 4，参数服从正态分布.采用简化Bishop法，基于材料参数均值计算得到的安全系数为1.159，与Cho[10]计算得到的1.164较为接近.

图 5 算例2路堤边坡剖面 Figure 5 Cross-section of the embankment built on a clay layer
图选项
表 4 算例2土体参数统计特性 Table 4 Statistical properties of soil parameters in Example 2
边坡土层 容重/(kN·m-3) 黏聚力/kPa 摩擦角/(°)
均值 COV 均值 COV
1 20 10 0.2 12 0.25
2 18 40 0.2 0 0
表选项

本例中训练样本个数为N=15D=45.算例2三种SVM模型参数优化结果见表 2，LSSVM模型优化过程见图 4.采用不同可靠度分析方法得到的失稳概率比较如表 5所示，智能响应面法计算结果和MCS以及其他系统可靠度分析方法计算结果基本一致.

表 5 算例2可靠度分析结果 Table 5 Results of probabilistic analysis for example 2
分析方法 失稳概率Pf/% 参考文献
系统可靠度界限法 22.7~44.9 [3]
分层RSM界限法 31.7~36.3 [19]
MCS(分层RSM) 35.75 [19]
MCS(最危险滑动面) 20.9(COV=3.2%) [9]
MCS(代表性滑动面) 35.6(COV=2.1%) [9]
MCS 20 000次抽样 36.555 [10]
多点FORM 35.939 [10]
FORM 20.6 [10]
MCS(GPR) 34.38(COV=0.4%) [15]
MCS(SVR) 34.39(COV=0.4%) [16]
MCS(ν-SVM) 34.62(COV=0.4%) [17]
MCS(LSSVM) 34.49(COV=0.4%) 本文
注：分析方法一栏括号内为响应面模型，GPR、SVR、ν-SVM、LSSVM抽样次数为105次.
表选项
3.3 ASCD测试题边坡

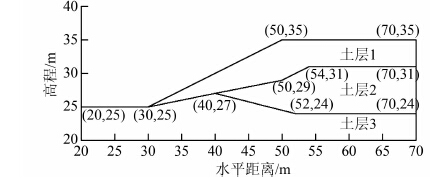
算例3改编自澳大利亚计算机辅助设计协会(ASCD)测试题[19]，边坡剖面见图 6，材料参数见表 6，不确定参数服从正态分布.采用著名岩土工程分析软件GeoStudio，基于简化Bishop法和材料参数均值计算的安全系数为1.405.

表 6 算例3土体参数统计特征 Table 6 Statistical properties of soil parameters in Example 3
边坡土层 容重/(kN·m-3) 黏聚力/kPa 摩擦角/(°)
均值 COV 均值 COV
1 19.5 0 NA 38 NA
2 19.5 5.3 0.3 23 0.2
3 19.5 7.2 0.3 20 0.2
表选项

本例中训练样本个数为N=15D=60.算例3三种SVM模型参数优化结果见表 2，LSSVM优化过程见图 4.采用不同可靠度分析方法得到的失稳概率比较如表 7所示，智能响应面法依然表现出较高的计算精度.

图 6 ASCD测试题边坡剖面 Figure 6 Cross-section of the ASCD testing slope
图选项
表 7 算例3不同方法可靠度分析结果 Table 7 Results of probabilistic analysis for example 3
分析方法 失稳概率Pf/% 参考文献
系统可靠度界限法 1.35~1.53 [19]
Slide V6.0抽样2万次 1.40 [19]
MCS(抽样50 000次) 1.33(COV=3.8%) [9]
MCS(最危险滑动面) 1.01(COV=4.4%) [9]
MCS(代表性滑动面) 1.08(COV=4.3%) [9]
MCS(GPR) 1.59(COV=0.8%) [15]
MCS(SVR) 1.41(COV=0.8%) [16]
MCS(ν-SVM) 1.43(COV=0.8%) [17]
MCS(LSSVM) 1.41(COV=0.8%) 本文
注：分析方法一栏括号内为响应面模型，GPR、SVR、ν-SVM、LSSVM抽样次数为106次.
表选项
4 计算效率分析

为体现智能响应面法在计算效率方面的优越性，对各个环节的计算时间进行了分析，其中智能响应面的建模时间见表 8，MCS抽样时间见表 9.GPR的建模时间较少，主要是因为采用共轭梯度法优化模型参数.另外3种响应面模型，采用ABC优化模型参数，建模时间稍长，其中LSSVM模型由于本身计算效率高于SVR和ν-SVM，其建模时间也明显较短.

表 8 智能响应面优化建模时间比较 Table 8 Time of modeling for intelligent RSM
算例 GPR SVR ν-SVM LSSVM
1 0.50 63.72 155.83 1.95
2 0.72 23.23 71.29 2.28
3 10-6 92.85 187.78 2.71
表选项
表 9 基于智能响应面的MCS时间 Table 9 Time of MCS using intelligent RSM
算例 GPR SVR ν-SVM LSSVM
1 4.26 2.48 2.46 2.43
2 5.10 3.11 3.01 3.24
3 5.79 5.20 5.20 3.73
表选项

在总体时间方面，以建模时间较长的ν-SVM模型为例来进行分析.3个算例采用简化Bishop法进行一次确定性边坡稳定分析需要7.46、5.82、5.79s，算例2采用Spencer法时需要8.39 s.采用ABC优化的ν-SVM模型，系统可靠度分析需要的时间分别为6.33、5.55、8.92 min，算例2采用Spencer法时需要7.63 min.该时间包含了样本安全系数计算时间、响应面模型优化时间和MCS(基于智能响应面法)抽样时间.然而直接蒙特卡罗法进行20 000次抽样分别需要41.44、32.33、32.17 h，算例2采用Spencer法时需要46.61 h[17].由此可以看出所提出智能响应面法在保持计算精度的同时，计算效率方面具有较大的优势.

5 结论

将几种具有较强非线性拟合能力的智能机器学习理论用于建立边坡体系可靠性分析智能响应面，提出了边坡系统可靠度分析智能响应面法一般框架及基于群体智能的模型参数优化一般流程，对GPR、SVR、ν-SVM、LSSVM多种智能响应面的性能进行了比较.得到如下结论：

1) GPR、SVR、ν-SVM、LSSVM等智能响应面模型用于边坡体系可靠性分析是有效的，体系可靠性分析智能响应面法获得的失效概率与直接蒙特卡罗法及其他系统可靠度分析方法获得的结果基本一致.

2) 所采用的几种智能响应面模型能够大幅度提高体系可靠性分析效率，从几个算例来看，分析时间可由直接MCS法的几十小时减少为几分钟.

3) 验证了拉丁方抽样样本个数N=15D时对于GPR、SVR、ν-SVM、LSSVM等几种模型来说可以达到较好的建模效果.

4) 所提出智能响应面法不需要搜索代表性滑动面，可减少很多复杂操作而得到失效概率的准确估计.但所研究问题没有考虑土体的空间变异性，对智能响应面法在此类问题上的应用还有待进一步深入研究.

参考文献
[1] Hassan A M, Wolff T F. Search algorithm for minimum reliability index of earth slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(4): 301–308. DOI:10.1061/(ASCE)1090-0241(1999)125:4(301)
[2] Oka Y, Wu T H. System reliability of slope stability[J]. Journal of Geotechnical Engineering, 1990, 116(8): 1185–1189. DOI:10.1061/(ASCE)0733-9410(1990)116:8(1185)
[3] Chowdhury R N, Xu D W. Geotechnical system reliability of slopes[J]. Reliability Engineering & System Safety, 1995, 47(3): 141–151.
[4] Low B K, Zhang J, Tang W H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope[J]. Computers and Geotechnics, 2011, 38(2): 196–204. DOI:10.1016/j.compgeo.2010.11.005
[5] Griffiths D V, Huang J, Fenton G A. Influence of spatial variability on slope reliability using 2-D random fields[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1367–1378. DOI:10.1061/(ASCE)GT.1943-5606.0000099
[6] Ching J, Phoon K K, Hu Y G. Efficient evaluation of reliability for slopes with circular slip surfaces using importance sampling[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(6): 768–777. DOI:10.1061/(ASCE)GT.1943-5606.0000035
[7] Wang Y, Cao Z J, Au S K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet[J]. Canadian Geotechnical Journal, 2011, 48(1): 162–172. DOI:10.1139/T10-044
[8] Li L, Wang Y, Cao Z, et al. Risk de-aggregation and system reliability analysis of slope stability using representative slip surfaces[J]. Computers and Geotechnics, 2013, 53: 95–105. DOI:10.1016/j.compgeo.2013.05.004
[9] Zhang J, Huang H W, Juang C H, et al. Extension of Hassan and Wolff method for system reliability analysis of soil slopes[J]. Engineering Geology, 2013, 160: 81–88. DOI:10.1016/j.enggeo.2013.03.029
[10] Cho S E. First-order reliability analysis of slope considering multiple failure modes[J]. Engineering Geology, 2013, 154: 98–105. DOI:10.1016/j.enggeo.2012.12.014
[11] Li D Q, Zheng D, Cao Z J, et al. Response surface methods for slope reliability analysis: Review and comparison[J]. Engineering Geology, 2015, 203: 3–14.
[12] Cho S E. Probabilistic stability analyses of slopes using the ANN-based response surface[J]. Computers and Geotechnics, 2009, 36(5): 787–797. DOI:10.1016/j.compgeo.2009.01.003
[13] Tan X H, Bi W H, Hou X L, et al. Reliability analysis using radial basis function networks and support vector machines[J]. Computers and Geotechnics, 2011, 38(2): 178–186. DOI:10.1016/j.compgeo.2010.11.002
[14] Zhang J, Huang H W, Phoon K K. Application of the Kriging-Based response surface method to the system reliability of soil slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(4): 651–655. DOI:10.1061/(ASCE)GT.1943-5606.0000801
[15] Kang F, Han S, Salgado R, et al. System probabilistic stability analysis of soil slopes using Gaussian process regression with Latin hypercube sampling[J]. Computers and Geotechnics, 2015, 63: 13–25. DOI:10.1016/j.compgeo.2014.08.010
[16] Kang F, Li J J. Artificial bee colony algorithm optimized support vector regression for system reliability analysis of slopes[J]. Journal of Computing in Civil Engineering, 2016, 30(3): 04015040. DOI:10.1061/(ASCE)CP.1943-5487.0000514
[17] Kang F, Xu Q, Li J J. Slope reliability analysis using surrogate models via new support vector machines with swarm intelligence[J]. Applied Mathematical Modelling, 2016, 40(11-12): 6105–6120. DOI:10.1016/j.apm.2016.01.050
[18] Suykens J A K, Van Gestel T, De Brabanter J, et al. Least Squares Support Vector Machines[M]. Singapore: World Scientific, 2002.
[19] Ji J, Low B K. Stratified response surfaces for system probabilistic evaluation of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(11): 1398–1406. DOI:10.1061/(ASCE)GT.1943-5606.0000711