文章信息
- 鞠程炜, 郝嘉凌, 杨晓松, 刘璐
- JU Chengwei, HAO Jialing, YANG Xiaosong, LIU Lu
- 台州东部新区围区海水入侵抗渗计算
- Calculation of antiseepage of seawater intrusion in Taizhou Eastern new reclamation area
- 武汉大学学报(工学版), 2018, 51(5): 394-400, 417
- Engineering Journal of Wuhan University, 2018, 51(5): 394-400, 417
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-004
-
文章历史
- 收稿日期: 2016-10-30
2. 山东省交通规划设计院,山东 济南 250000;
3. 江苏方洋集团有限公司,江苏 连云港 222000
2. Shandong Provincial Communications Planning and Design Institute, Jinan 250000, China;
3. Jiangsu Fang Yang Group Ltd., Lianyungang 222000, China
随着沿海地区经济的高速发展和海岸带的利用与开发,沿海各地区许多国家都不同程度出现了海水地下入侵情况[1],在我国,主要集中在渤海和黄海这片区域.海水入侵不仅危害当地经济的发展,更对生态环境有很大的破坏.国内外均很重视海水入侵的研究与治理,主要体现在堤身防渗材料的选择方面,并取得了较好效果.而对于经海堤地基海水地下入侵及抗渗研究,仍然存在难度,主要原因是经堤基土的海水入侵现象较为复杂,且缺少现场实测资料,难以了解海水入侵的过程变化.
台州市位于浙江省沿海中部,地处台州湾南侧(图 1).改革开放以来,台州市实现了经济的高速增长,为保持增长态势,解决土地资源紧张状况,台州市启用东部新区围垦项目(图 2)作为未来产业中心,发展循环经济,打造生态水城,提出月湖绿岛、公园水网的新概念,即在围区中心布置一个人工湖——月湖,其淡水系统有利于维护围区生态环境.由于围区地质土渗透性较强,受海堤堤基渗流入侵影响,水质中盐分不仅会对月湖及周边的生态环境产生破坏,而且因月湖与周围水系组成了相互连通的水网,一旦其水质受到破坏,将对围区内整体生态环境产生连锁破坏效应,亟需寻求有效解决海水入侵方法,控制月湖淡水中盐分浓度,使邻近月湖区域不受海水入侵的影响.

|
| 图 1 台州地理位置图 Figure 1 Taizhou location map |

|
| 图 2 围区布置图 Figure 2 Reclamation project area layout |
海水入侵的本质是由于外海海水产生的涨潮水位高于围区地面高程,形成了水头差,且在水头差作用下,海水经海堤堤身及堤基土的空隙产生渗流,同时因海水盐分含量远高于陆地地下水盐分含量[2],在海水向围区内渗流的过程中盐分也随着向内转移、扩散,造成土质的盐碱化.因此,外海海水水头是海水入侵发生的重要因素,其水头变化与区域潮汐特性有关.
本区域外海潮汐属浅海正规半日潮,每次涨潮和落潮大约为6 h,潮流的涨潮方向基本上由东南向西北,落潮方向相反.潮位过程选取非汛期10年一遇潮型(见图 3).

|
| 图 3 潮位过程曲线图 Figure 3 Tide process graph |
海堤是沿海地区挡潮抗浪的护岸建筑物,外海潮水在潮汐作用下经海堤堤身和堤基渗流至围区,形成海水入侵.海堤渗流通常分为两个部分,一个是堤身渗流,一个是海堤基础渗流[3],由此可见海堤堤身断面的材料及结构型式对海水渗流尤为重要.
东部新区海堤断面为混合式,其断面结构见图 4,海堤的堤顶宽度为6.8 m,顶部的高程为8.2 m,防浪墙顶高程9.0 m,堤顶基础均座落于块石子堤上.堤顶基面采用0.20 m厚的碎石垫层和0.20 m厚的5%水泥,路面采用厚0.20 m的C20砼浇筑.堤顶坝面结合排水需要,自外向内倾斜,坡度为2%.堤身采用土石混合结构,地基处理层上部采用机械抛填块石混合料,顶高程至4.00 m,上部设块石型砌子堤(背水侧)和C20砼灌砌块石重力墙(迎水侧).子堤顶宽4.00 m,内坡1:1.0,与防渗土之间设过渡反滤层.重力墙内侧直立,外侧1:0.4.防浪墙基础座落于重力墙上,采用“L”形C20砼结构.外海侧采用C20细石砼灌砌块石、干砌块石、3 t四角空心块等3种方式联合进行防护.内坡采用淤泥质黏土防渗体,一级平台顶高程7.0 m,顶宽6.0 m,坡度1:4;二级平顶高程4.5 m,顶宽8.00 m,坡度1:12;三级平台顶高程2.50 m,顶宽12 m,坡度1:3.0,对一级、二级平台采用干砌石保护,对二级平台斜坡采用三维土工网绿化固土处理.

|
| 图 4 海堤典型断面结构 Figure 4 Cross-sectional structure of typical sea dyke |
海水渗流在透过海堤后,堤后的地质情况会对海水的进一步渗流产生影响.围区项目的地层基础是海堤渗流模型的主体部分,每层的地质参数都对建模的准确性有很大的影响.根据钻孔取样及静力触探揭示,工程区地层自上而下主要分别为淤泥、淤泥夹粉土、淤泥或淤泥质黏土、黏土4层,主要盐分离子有Ca2+、Mg2+、Na+、K+、CO32-、HCO3-、Cl-和SO42-.在勘察深度40.20 m范围内,自上而下各土层工程地质特征如下:
1) 第1层为淤泥地层,物理力学参数指标:含水量49.9%~62.8%,湿密度16.1~17.7 kN/m3,孔隙比为1.370~1.690,压缩模量1.75~3.04 MPa.
2) 第2层为淤泥夹粉土,厚度0.5~11.10 m,物理力学参数指标:含水量40.1%~56.0%,湿密度16.88~18.2 kN/m3,孔隙比为1.030~1.538,压缩模量为1.55~3.87 MPa.
3) 第3层为淤泥,一般厚度10.0~19.0 m,物理力学参数指标:含水量44.0%~65.5%,湿密度16.1~17.7 kN/m3,孔隙比为1.242~1.805,压缩模量1.16~2.65 MPa.
4) 第4层为黏土,最大厚度取到20.20 m,物理力学参数指标:含水量30.6%~46.0%,湿密度17.1~18.7 kN/m3,孔隙比为0.913~1.321,压缩模量2.40~4.06 MPa.
具体的每层地基土颗粒分析见表 1,其中d60、d30、d10分别相当于小于某粒径土重累计百分含量的60%、30%及10%对应的粒径,分别称为限制粒径、中值粒径和有效粒径.
| 土层 | 地基名称 | 不同粒径地基土颗粒含量/% | d60/mm | d30/mm | d10mm | ||||
| 0.1~0.05 mm | 0.05~0.01 mm | 0.01~0.005 mm | 0.005~0.002 mm | < 0.002 mm | |||||
| 1 | 淤泥 | 5.60 | 46.76 | 14.7 | 13.80 | 19.1 | 0.010 | 0.006 | 0.001 |
| 2 | 粉土 | 5.80 | 53.43 | 12.8 | 9.37 | 18.6 | 0.019 | 0.007 | 0.001 |
| 3 | 淤泥 | 5.40 | 44.30 | 16.9 | 12.70 | 20.6 | 0.010 | 0.005 | 0.001 |
| 4 | 黏土 | 4.39 | 39.18 | 18.7 | 15.07 | 22.4 | 0.012 | 0.004 | 0.001 |
描述土壤水分特征曲线的Van Genuchten方程基本表达式为
 (1)
(1)
式中:θ(h)是土壤体积含水量,cm3/cm3;θs和θr分别为土壤饱和含水量和残余含水量;h为压力水头,cm;α是与进气吸力相关的参数;m和n为土壤水分特征曲线的形状系数,m=1-1/n.
Geo-Studio软件SEEP/W模块自带土-水特征曲线模拟功能,基于Van Genuchten方程可评估出合理的体积含水量与基质吸力的关系曲线[4].借助Geo-Studio软件,根据土体的颗粒级配曲线(表 1),描绘地基和内部土体应力随含水量变化的过程,描述水土二相对土体相互影响相互制约的耦合关系.对在海水渗流时这一特殊的双向饱和-非饱和非稳定渗流场进行模拟[5],结果见图 5.以含水度和基质吸力的关系曲线为基础,进而可以模拟出在含水度不断变化的过程中渗透系数的变化,将这种关系通过拟合曲线的形式表达出来.渗透系数与基质吸力关系曲线见图 6.以上两种曲线将作为渗流模型中地基基础的定义参数.

|
| 图 5 不同土层的体积含水量与基质吸力关系曲线 Figure 5 Volumetric water content and matrix suction relation curve of different soil layers |

|
| 图 6 不同土层的渗透系数与基质吸力关系曲线 Figure 6 X-Conductivity and matrix suction of different soil layers |
采用的Geo-Studio软件的建模程序是平面二维模式——垂直方向和水平延伸方向.为了确保渗流模型的准确性,要求模拟对象应具有以下3个条件:
1) 海岸线较为平整.
2) 沿海向内陆延伸的一定封闭区域内,地势平缓,地质构造分层且稳定.
3) 拥有挡水建筑物保护岸线.
依据上述条件,拟建模研究围区海水入侵抗渗计算代表断面位于月湖中段,月湖至海堤之间水平距离约1 000 m,挡潮海堤长度3.0多km,其间地势起伏不大,地质构造较为稳定,垂直方向(地基土层)范围可自上而下取4层地质,计算区域的边界:内陆侧为月湖,沿海侧为已建海堤.因此根据模型的计算范围,边界条件包括月湖水位及其氯离子浓度、海水水位及其氯离子浓度.其中海水水位可以通过潮位变化曲线来设置,月湖水位则需要通过分析研究来确定[6-11].
利用Geo-Studio建立的渗流二维模型空间(图 7)左端为围区内陆侧,右端为沿海侧,自左向右沿地势分布长度为1 400 m,地层深度基准为40 m.以右端海堤模块及右侧边界长度为15 m的地基模块作为海水水头边界,海堤模块依据1.2节中海堤的典型断面形式所定义,地基模块依据1.3节中地质资料自上而下布置为4层:第1层为淤泥,厚度为4.29 m;第2层为淤泥夹粉砂,厚度为7 m;第3层为淤泥,厚度为16.45 m;第4层为黏土,其厚度为9.88 m,每层地基的土质特性遵循图 5、6中的土水特性曲线.模型主要研究月湖至海堤之间渗流的形成,氯离子在渗流过程中的浓度扩散.

|
| 图 7 围区二维渗流模型 Figure 7 Reclamation two-dimensional seepage model |
通过对围区沿海水质进行抽样检查,选取围区内高低潮期各区一组水样,水质分析结果见表 2.由于受海水入侵影响,围区土海水中氯离子比其他离子的含量高,是影响围区生态环境的主要物质,其在地下渗流中含量的变化可视为评判海水入侵发生程度的标准.所以在模型中选取低潮样本中氯化物的含量11 527 mg/L作为边界离子浓度.
| 取样时刻 | pH | 含量/(mg·L-1) | |||||
| 氯化物 | 高锰酸盐指数 | 游离二氧化碳 | 侵蚀性二氧化碳 | 硫酸盐 | 溶解性总固体 | ||
| 高潮期 | 8.10 | 10 846 | 19.6 | 0.00 | 0.00 | 793 | 21 825 |
| 低潮期 | 8.10 | 11 527 | 19.4 | 0.00 | 0.00 | 860 | 22 781 |
海水入侵数学模型的控制方程主要有两个,一个是描述地下渗流过程中由于水头变化和浓度变化而运动特性也在不断改变的过程,另一个是描述地下水中离子浓度转移和分布的过程.
第一个方程简称为水头方程,由Darcy定律、欧拉方程和采用Huyakorn的线性处理可得:
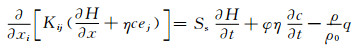 (2)
(2)
式中:Kij表示渗透系数的张量形式,i, j=1, 2;H为淡水区域的水头;xi、xj为自定义坐标,i, j=1, 2;η为密度耦合的系数,η=ε/cs;ε=(ρs-ρ0)/ρ0,为密度差率;cs、ρs分别为海水浓度和密度;c、ρ分别为地下水浓度和密度;ρ0为淡水密度;ej为重力方向的第j个分量;Ss为贮水率;t为时间;φ为孔隙度;q为表示单位体积下源(或汇)定额时间内的流量.
对潜水含水层来说,对应的初始条件和边界条件有
 (3)
(3)
 (4)
(4)
 (5)
(5)
式中:H0为水头初值;H为第一类边界Γ1上给定的水头;n=(n1, n2),为定义的第二类边界Γ2、B2和潜水面Γ2-1上的外法向单位矢量;vn为Γ2上给定的单位面积侧向流量(流入为正,流出为负).
第二个综合方程是描述地下渗流中盐分的运移,经研究表明,可采用下面的对流-弥散方程:
 (6)
(6)
式中:Dij为弥散系数张量;v=(v1, v2),为地下水实际平均速度矢量; c*为注入(或抽出)液体浓度,相应的初始条件和边界条件为
 (7)
(7)
 (8)
(8)
 (9)
(9)
式中:c0为浓度初值; c为第一类边界B1上给定的浓度;B2为隔水边界.
2.3 围区海水入侵的抗渗计算治理海水入侵的一个思路是对已建海堤建筑物进行防渗再处理,由于围区区域面积大,海堤长度有3 000多m,如果对现已建成的海堤进行重新整修,需要大量资金.另一个思路是通过补给地下水形成淡水帷幕,增加内陆淡水水头,控制界面的移动.高学平(2006)[12]通过建立剖面二维非均匀流体的对流-扩散有限元模型,对广西北海海城的海水入侵几种治理方案和方法进行了模拟,论证了帷幕方式防止海水入侵的可行性.考虑到围区建设规划方案中已布置内陆湖泊——月湖,可以利用月湖蓄水的水头产生渗流,反向运动与海水产生的渗流交汇,对海水渗流既有阻挡抑制作用又降低渗流两端的浓度差,对此,则需要计算分析月湖水位变化及水头差是否能将海水入渗控制在对围区影响的较小范围.
若想要利用月湖蓄水来抑制海水入侵,需对月湖不同水位产生的淡水渗流阻挡作用进行评估.根据围区运行防洪规划及排涝能力,围区防洪月湖最高控制水位为2.68 m,月湖的日常水位为0.6~2.68 m.采用渗流模型模拟计算不同水位下渗流和氯离子的扩散,月湖水位从0.6 m开始,以0.3 m为水头梯度,依次取0.6、0.9、1.2、1.5、1.8、2.1、2.4、2.7 m模拟,并对计算结果进分析、比较与研究.
代表水位0.6 m时计算结果见图 8、9,其他水位下计算结果见表 2、3.

|
| 图 8 水位为0.6 m时渗流稳定计算图 Figure 8 Seepage stability calculation map on 0.6 m water level |

|
| 图 9 水位为0.6 m时浓度扩散稳定计算图 Figure 9 Concentration diffusion stability calculation map on 0.6 m water level |
| m | |||||||
| 月湖水位/m | > 10 000 mg/L | 8 000~10 000 mg/L | 6 000~8 000 mg/L | 4 000~6 000 mg/L | 2 000~4 000 mg/L | 严重区 | 超标区 |
| 0.6 | 300 | 200 | 160 | 140 | 180 | 500 | 980 |
| 0.9 | 260 | 180 | 150 | 140 | 130 | 440 | 960 |
| 1.2 | 250 | 170 | 140 | 130 | 120 | 420 | 810 |
| 1.5 | 230 | 140 | 100 | 100 | 120 | 370 | 690 |
| 1.8 | 220 | 130 | 90 | 100 | 120 | 350 | 660 |
| 2.1 | 210 | 110 | 90 | 80 | 100 | 320 | 590 |
| 2.4 | 200 | 100 | 80 | 80 | 100 | 300 | 560 |
| 2.7 | 170 | 140 | 80 | 80 | 100 | 320 | 570 |
从整个模拟过程可以看出,在渗流推进过程中,月湖淡水水头产生的渗流与海水水头产生的渗流分别推进,在月湖与外海之间交汇,形成完整的渗流体系;氯离子随着海水渗流向前扩散,在海水渗流与淡水渗流尚未交汇前,氯离子的扩散较快,在交汇后,扩散速度会因受到淡水渗流的影响而慢下来[6].同时从图 5、6中可以看出,在海水渗流的作用下,渗流稳定后,超标区(氯离子浓度高出正常标准)的范围有980 m,月湖至海堤区域长约1 100 m,由此可见这片范围内的大部分土地都会受到氯离子的侵袭,存在发生盐碱化[13]的趋势.
2.4 计算结果分析1) 不同水位下氯离子浓度结果统计
对不同月湖水位下氯离子浓度的分布进行统计,得出月湖至海堤段严重带(氯离子浓度过高)、超标带(氯离子浓度高出正常标准)和安全带的长度(表 3).因为氯离子的浓度是海水渗流产生的,浓度变化从海岸向内陆依次递减,所以严重区主要集中在海堤堤身附近的区域[14-16].
为更直观地研究海水渗流下氯离子浓度扩散的规律,并分析浓度扩散后对月湖附近生态环境的影响范围,将表 3中数据绘制影响范围进行对比和分析,如图 10所示.

|
| 图 10 海水入渗计算影响范围 Figure 10 The calculation influence range of seawater intrusion |
同时为更准确确定抑制海水入侵的水位,在距离月湖900 m的典型断面上同一高程处自左向右选取8个观察点,研究这8个点在月湖水位变化的情况下随海堤渗流所发生的浓度变化,其统计结果见表 4.
| 观察点 | 氯离子浓度/(mg·L-1) | |||||||
| ▽0.6 m | ▽0.9 m | ▽1.2 m | ▽1.5 m | ▽1.8 m | ▽2.1 m | ▽2.4 m | ▽2.7 m | |
| 1 | 7 971 | 7 255 | 6 891 | 5 348 | 4 965 | 3 883 | 3 093 | 3 072 |
| 2 | 7 938 | 7 251 | 6 887 | 5 342 | 4 960 | 3 880 | 3 097 | 3 072 |
| 3 | 7 940 | 7 242 | 6 882 | 5 276 | 4 949 | 3 971 | 3 433 | 3 334 |
| 4 | 7 939 | 7 232 | 6 872 | 5 224 | 4 931 | 3 997 | 3 548 | 3 469 |
| 5 | 7 938 | 7 225 | 6 864 | 5 186 | 4 916 | 4 000 | 3 581 | 3 552 |
| 6 | 7 938 | 7 220 | 6 858 | 5 161 | 4 905 | 3 989 | 3 568 | 3 589 |
| 7 | 7 934 | 7 197 | 6 834 | 5 042 | 4 839 | 3 828 | 3 262 | 3 633 |
| 8 | 7 933 | 7 190 | 6 826 | 5 001 | 4 815 | 3 758 | 3 130 | 3 627 |
1) 当月湖水位从0.6 m依次增加至2.7 m,海水入侵所造成的氯离子浓度超标的范围不断缩小,超标区从980 m缩减570 m,而严重区从500 m缩减至320 m.氯离子浓度一步步地降低,从7 000多mg/L降低至3 000多mg/L,这说明淡水水位的提高对咸水产生的入侵有明显的抑制效果.
2) 月湖水位为2.1、2.4、2.7 m时,超标区范围分别为590、560、570 m,说明水位接近2.1 m时,氯离子浓度扩散的范围已经变化很小了.在2.1 m这个水位时,扣除海堤堤身长度200 m,氯离子超标的范围会被控制在堤身后390 m左右,此时距离月湖还有800 m,说明海水入侵对月湖附近的生态环境影响已经非常小.
这些现象说明由于淡水水头提高会缩小与海水的水头差,淡水渗流产生的作用会变大,对海水产生的渗流推进造成了抑制,在这种抑制作用下,随海水渗流向内陆扩散的氯离子受到了抑制.同时,月湖水头增大到一定程度时,与外海的水头差不再是推动氯离子扩散的因素,这时氯离子的扩散主要以浓度差为动力,即淡水水头的抑制作用会达到极限,氯离子扩散的范围几乎不会随之变化.
2) 涨落潮时海水入侵分析
为了对计算的现象有清楚认识,便于分析和研究渗流变化,选取月湖典型水位2.1 m时涨潮和落潮分别稳定效果图,通过观察稳定时交汇界面的迁移来观测涨落潮对海水入侵的影响.
通过对比图 11(a)、(b),可以看出在氯离子扩散稳定下来后,稳定界面并不是一成不变的,而是随着潮汐的涨落不断振荡.自涨潮开始时起,稳定界面慢慢向内陆侧移动,在达到潮位最高时,稳定界面也濒临达到内陆侧方向的极限值;在落潮开始时,稳定界面也开始回收,在潮位最低时,稳定界面濒临达到外海侧方向的极限值.可见稳定界面会随着潮汐的进行周而复始的迁移.

|
| 图 11 浓度扩散稳定计算图 Figure 11 Concentration diffusion stability calculation map |
同时,可以看到在水位2.1 m时,无论涨潮还是落潮,距月湖的安全距离都超过了800 m,水位在2.1 m时对涨落潮时海水入侵有明显抑制作用.
3 结论本文以台州东部新区围区建设项目中存在的海水地下入侵渗透问题为研究对象,基于围区建设的基本条件,利用Geo-Studio软件计算研究月湖蓄水(水位0.6~2.7 m)的反向抗渗效果,主要结论如下:
1) 外海与围区内的水头差、浓度差、潮位变化、围区的地质指标是海水地下入侵的主要影响因素;无抗渗措施时,海水入侵影响的范围非常大,对围区生态破坏严重.
2) 氯离子的浓度是海水渗流产生的,浓度变化的趋势是从海岸向内陆依次递减,外海与内陆的水头差是推动氯离子扩散的主要因素,当水头差达到一定程度时,淡水水头的抑制作用会达到极限,氯离子的扩散主要以浓度差为动力.
3) 淡水水位的提高对咸水产生的入侵有明显的抑制效果.月湖水位为2.1~2.68 m时,可以达到消除海水入侵的效果.围区防洪月湖最高控制水位为2.68 m,则月湖蓄水位达到2.1~2.68 m是可以实现的,有利于阻挡与减缓海水入侵.
| [1] |
郭占荣, 黄奕普. 海水入侵问题研究综述[J].
水文, 2003, 23(3): 10–15.
Guo Zhanrong, Huang Yipu. Comprehensive study on seawater intrusion[J]. Hydrology, 2003, 23(3): 10–15. |
| [2] | Lazarov R D, Mishev I D, Vassilevski P S. Finite volume method for convection-diffusion problems[J]. SIAM J. Numer Anal, 1996, 33(1): 31–55. DOI:10.1137/0733003 |
| [3] |
刘鹏. 考虑渗流作用的海堤稳定性分析[J].
价值工程, 2010, 29(33): 274–274.
Liu Peng. Coastal levee stability study taking into consideration of seepage[J]. Value Engineering, 2010, 29(33): 274–274. DOI:10.3969/j.issn.1006-4311.2010.33.256 |
| [4] |
来剑斌, 王全九. 土壤水分特征曲线模型比较分析[J].
水土保持学报, 2003, 17(1): 137–140.
Lai Jianbin, Wang Quanjiu. Comparison of soil water retention curve model[J]. Journal of Soil and Water Conservation, 2003, 17(1): 137–140. |
| [5] |
王海华, 陈德春, 亢扬. 条子泥一期匡围截流堤失稳与接面抗渗破坏对策方案[J].
江南大学学报, 2014, 13(5): 576–582.
Wang Haihua, Chen Dechun, Kang Yang. Unstability analysis and junction permeability damage countermeasure research of Tiaozini First-Phase Closure dike[J]. Journal of Jiangnan University, 2014, 13(5): 576–582. |
| [6] | Ghassemi F, Jakeman A J, Jacobson G. Mathematical modeling of sea water intrusion[J]. Nauru Island.Hydrol Process, 1990, 4: 269–235. DOI:10.1002/(ISSN)1099-1085 |
| [7] | Estabragh A R, Soltani A, Javadi A A. Models for predicting the seepage velocity and seepage force in a fiber reinforced silty soil[J]. Computers and Geotechnics, 2016, 75: 174–181. DOI:10.1016/j.compgeo.2016.02.002 |
| [8] | Naoya Masaoka, Ken'ichirou Kosugi, Yosuke Yamakawa, et al. Processes of bedrock groundwater seepage and their effects on soil water fluxes in a foot slope area[J]. Journal of Hydrology, 2016, 535: 5–83. |
| [9] | Zhao Chongbin, Schaubs P, Hobbs B E. Computational simulation of seepage instability problems in fluid-saturated porous rocks: Potential dynamic mechanisms for controlling mineralisation patterns[J]. Ore Geology Reviews, 2016, 79: 180–188. DOI:10.1016/j.oregeorev.2016.05.002 |
| [10] | Garey A Fox, Rachel G Felice. Bank undercutting and tension failure by groundwater seepage: Predicting failure mechanisms[J]. Earth Surf. Process. Landforms, 2014, 39(6): 758–765. DOI:10.1002/esp.v39.6 |
| [11] | Bereslavskii é N. Some cases of seepage in dams with a vertical upstream face and base drainage[J]. Fluid Dynamics, 1992, 26(6): 841–844. DOI:10.1007/BF01056784 |
| [12] |
高学平, 杨建华, 涂向阳, 等. 帷幕防治海水入侵的数值模拟研究[J].
环境污染与防治, 2006, 25(11): 55–58.
Gao Xueping, Yang Jianhua, Tu Xiangyang, et al. Study on numerical simulation for control of seawater intrusion through barriers[J]. Environmental Pollution and Control, 2006, 25(11): 55–58. |
| [13] | Yuan G W, Hang X D, Sheng Z Q, Yue J Y. Progress in numerical methods for radiation diffusion equations[J]. Chinese J. Comput Phys, 2009, 26(4): 475–500. |
| [14] | Ye Haiwang, Li Wen. Dynamic stability analysis and forecast of surface mine dump[J]. Open Journal of Safety Science and Technology, 2012, 2(2): 55–61. DOI:10.4236/ojsst.2012.22008 |
| [15] | Monal Raj, Aniruddha Sengupta. Rain-triggered slope failure of the railway embankment at Malda[J]. India. Acta Geotechnic, 2014, 9(5): 789–798. DOI:10.1007/s11440-014-0345-9 |
| [16] | Mohammad Asif Raja. Behaviour of earth dam under seismic load considering nonlinearity of the soil[J]. Open Journal of Civil Engineering, 2016, 6(2): 75–83. DOI:10.4236/ojce.2016.62007 |
 2018, Vol. 51
2018, Vol. 51




