文章信息
- 余智, 张凤亮, 熊海贝
- YU Zhi, ZHANG Fengliang, XIONG Haibei
- 基于线性累计损伤理论的预应力混凝土风电塔架疲劳可靠性及剩余寿命研究
- Fatigue reliability and remaining life analysis of prestressed concrete wind turbine towers based on linear cumulative damage rule
- 武汉大学学报(工学版), 2016, 49(5): 756-762
- Engineering Journal of Wuhan University, 2016, 49(5): 756-762
- http://dx.doi.org/10.14188/j.1671-8844.2016-05-019
-
文章历史
- 收稿日期: 2016-04-20
在新兴能源中,风能因洁净、环保、成本低和可再生等优势而受到各个国家的重视.近年来,风力发电系统在我国发展迅猛,混凝土塔架由于其刚度大、耐久性好等特性越来越多地应用于各大风场中.风电塔架是风力发电系统的承重结构,同时还承受风荷载等随机荷载的作用,风荷载可使风电塔架因疲劳导致强度不足而破坏.因此,对随机风荷载作用下的塔架进行疲劳分析的研究具有重要的科学意义和实用价值.
风力发电塔架属于高耸结构,其风致疲劳属于随机变幅疲劳问题,此类问题的研究多采用S-N曲线及线性累计损伤理论.Albert A. Petrov[1]提出预测结构的使用寿命时需要考虑风荷载的随机作用,通过计算结构在风荷载下的疲劳损伤可以得出其使用寿命,结合当地的风载资料、结构所使用材料的疲劳特性以及结构动力响应得出其平均寿命;Robertson[2]等对圆柱体结构进行了风振疲劳试验,并根据实测数据计算了结构的疲劳寿命;欧进萍[3]等用概率方法研究了结构的风振疲劳累积损伤问题;刘胜祥[4]等基于线性累计损伤提出估算海上风力塔架寿命的方法,用雨流计数法对循环应力进行循环参量的统计,通过等寿命转换将其转换为对称循环应力谱,分析变幅应力谱下塔架的疲劳损伤并估算其疲劳寿命;王永玲[5]对塔架在不同风况下的响应进行模拟,利用最小二乘法对数据进行直线拟合,从而获得塔架的S-N曲线,根据经验估计出塔架设计载荷谱,结合Miner损伤理论,对风机塔架作出寿命评估.
目前尚未发现有相关文献对预应力混凝土风力发电塔进行相关研究,本文在上述研究的基础上,以预应力钢筋混凝土风电塔架为研究对象,利用有限元软件建立塔架模型,之后采用谐波叠加法[6](WAWS法)模拟出不同风速下的随机风荷载时程样本,结合有限元软件计算出风电塔架在不同风速下的动力响应,提取出疲劳关键点的应力谱,通过雨流计数法统计出随机应力幅及其相应的循环次数,得出相应风速下各应力幅在设计使用年限内总的循环次数,最后基于Miner线性累计损伤准则和预应力钢筋的S-N曲线求出对塔架关键点的疲劳可靠指标并估算出塔架的剩余疲劳寿命.
1 预应力混凝土风力发电塔架结构疲劳分析 1.1 预应力混凝土风电塔架疲劳特性疲劳可以从不同的角度分类,从微观上看,疲劳裂纹与其局部微观塑性有关.从宏观上看,循环应力水平较低时,结构的疲劳寿命较长,称为高周疲劳或者是应力疲劳;反之,结构的疲劳寿命相对较短,称之为低周疲劳或者是应变疲劳.风电塔架在作用载荷下产生的应力一般比较小,但是由于风机时时在运行及风荷载的频繁作用,使得其应力循环次数较高,因而,在风荷载作用下,风电塔架一般会发生高周疲劳.
研究[7, 8]表明,钢筋混凝土结构在受到疲劳荷载时,受压区的混凝土一般不作为重点关注对象,而受力钢筋的疲劳损伤程度成为重要的关注对象,受力钢筋的疲劳破坏往往标志着钢筋混凝土构件的疲劳破坏,因而目前工程界通常以钢筋材料的疲劳寿命作为钢筋混凝土结构疲劳寿命预测的基础.而在预应力混凝土结构中,由于在使用过程中预应力钢筋通常始终保持着较高的应力水平且预应力钢筋的重要性远高于普通钢筋,而一般认为当应力范围相同时,平均应力越高结构的疲劳寿命越低[9].故预应力钢筋的疲劳比普通钢筋更值得关注.
1.2 预应力钢筋S-N曲线铁科院相关技术人员[10]对预应力钢绞线的疲劳性能进行了研究,对一批fpk=1 860 MPa的钢绞线进行了疲劳试验,根据试验结果并取99.7%保证率得到1 860级预应力钢绞线的S-N曲线表达式:
式中:N为疲劳寿命;S为疲劳应力幅.
式(1)是常用的疲劳失效的经典模型,它是在常幅循环应力作用下疲劳试验的基础上建立起来的,该疲劳模式适用于等幅应力下的高周疲劳,该模型中的平均应力等于0,然而对于实际工程结构,在循环荷载作用下其应力的平均值通常不等于0,这时就需要考虑平均应力的影响将循环应力幅值S按Goodman换算公式进行处理:
式中:Sa0为零平均应力的应力幅;Sa为非零平均应力的应力幅;Sm为平均应力;St为材料的抗拉强度.
1.3 Miner线性累积损伤理论风力发电系统在正常使用过程中总是处于变幅应力循环作用下,载荷每循环一次,使得构件承受大于疲劳极限的应力时,材料就会受到一定的损伤,随着循环次数的增加,损伤的累积逐渐增大,最终导致结构疲劳破坏,这就是疲劳累积损伤理论,疲劳累积损伤准则是评估结构疲劳寿命的常用方法.本文选用Miner线性疲劳损伤理论,其假定为[9]
1) 如果将某一荷载块的应力循环数表示为相同应力幅下造成破坏所需总应力循环数的百分数,则这一百分数就是该荷载块所消耗的变幅疲劳寿命的百分数;
2) 荷载块的顺序不影响疲劳寿命;
3) 当每个荷载水平引起的损伤的线性累加和达到临界值,则结构发生破坏.
在含有k个荷载块的加载序列中,如果用ni表示应力幅Si的实际应力循环次数,Ni表示该应力幅对应的破坏循环次数,则Miner线性累计损伤理论表述为
按一次二阶矩可靠度分析方法,构件的失效概率可由可靠指标β来表达.极限状态方程为
当假定ΔσR、Δσe均近似服从对数正态分布且二者相互独立时,先将其改写为等效的极限状态方程:
式中,lnΔσR和lnΔσe服从正态分布.由一次二阶矩方法求得构件的疲劳可靠指标为
式中:lnΔσR为lnΔσR的均值;lnΔσe为lnΔσe的均值;σlnΔσR为lnΔσR的标准差;σlnΔσe为lnΔσe的标准差.
通常抗力S-R曲线是在常用对数(以10为底)坐标中进行回归的,且所给出的lgΔσR-lgN的值都是取97.73%保证率,即均值减去2倍标准差的值,故$\lg \Delta {{\sigma }_{R}}=\overline{\lg \Delta {{\sigma }_{R}}}-2{{S}_{R}}$,即
式中,SR=σlgΔσR,为疲劳抗力常用对数lgΔσR的标准差.
为了应用方便,将式(6)变换成以常用对数表达的形式,由对数换底公式得
将式(8)~(12)代入式(6)中,得
式中,Se=σlgΔσe,为等效等幅应力常用对数lgΔσe的标准差;lgΔσR为构件疲劳抗力常用对数的均值;lgΔσe为设计基准期内疲劳荷载等效等幅应力常用对数的均值.
将$\overline{\lg \Delta {{\sigma }_{e}}}=\lg \overline{\Delta {{\sigma }_{e}}}$代入式(13),得疲劳可靠指标如下式所示:
由可靠指标可得失效概率的公式:
雨流计数法又可称为“塔顶法”,由英国的工程师Matsuiski和Endo提出的,距今已有50多年.雨流计数法在工程中应用得较多,尤其是在计算疲劳寿命时应用更加广泛[12].雨流计数法一般分为数据压缩、载荷时间历程的调整以及循环提取3个步骤完成.
按照一般的雨流计数法原则对疲劳应力时程的峰谷值提取循环块主要分成两个阶段,即一次雨流计数和二次雨流计数,在进行二次雨流计数之前需要对数组进行对接.经过对疲劳关键点的应力时程曲线预先处理,循环块的提取不需要进行对接即可完成[13].
对本研究中的预应力混凝土塔架模型来说,进行完风荷载作用下的动力分析后,取出对疲劳关键点单元的应力时程分别进行雨流计数,将各单元的应力时程储存于数组中,按照以下步骤依次完成.
2.1 数据压缩数据压缩就是将原始的应力时程处理成便于计取循环数的数组,包括相邻等值数压缩、峰谷值检测和无效幅值去除.
1) 相邻等值数压缩.即判断应力时程前后两个元素是否相等,若相等则只保留一个.
2) 峰谷值监测.判断经压缩后的数组相邻数值之差的乘积是否>0,若>0则提取峰(或谷)值.
3) 无效幅值去除.即将幅值很小的点去除.对于无效幅值的省略,目前还没有统一的准则,为了便于对不同载荷时间历程所省略的无效幅值进行统一,文中采用董乐义[12]推荐的公式进行无效幅值的舍弃.
2.2 载荷时间历程调整[14]1) 调整峰谷值.判断数组的峰谷值点总数是奇数还是偶数,若为奇数,则对应力时程不做处理;若为偶数,则去掉最后一个点.判断首尾点是峰值还是谷值,若是峰值,则使首尾两点的值都取二者中的较大者;若是谷值,则使首尾两点的值都取二者中的较小者.
2) 重新对接.寻找经上述调整后的应力时程中的最高波峰(最低波谷)点,将应力时程从该点处截断,将左段的起点与右段的末点对接,使新的应力时程首尾均为最高波峰(最低波谷)点.
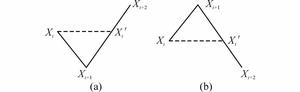
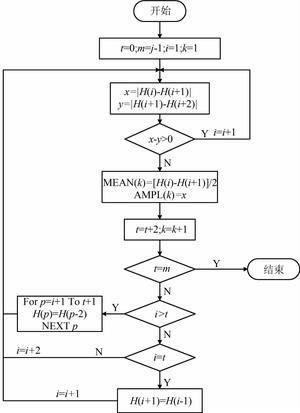
2.3 循环提取用雨流计数法[13]对应力时程进行雨流计数,即按照“三峰谷计数原则”对历程计数,从头反复寻找如图 1所示的波形,具体流程如图 2所示.图中,H(i)为经历过上述调整后的应力时程,j为H(i)的长度,最终寻找出来的各个循环均值和幅值分别存放在数组MEAN(k)和AMPL(k)中.
|
| 图 1 循环提取的波形 Figure 1 Wave extracted |
|
| 图 2 雨流计数法循环提取图 Figure 2 Flowchart by rain-flow counting method |
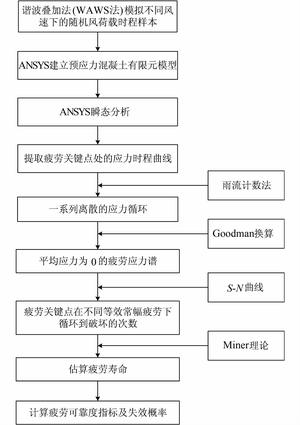
对预应力钢筋混凝土风电塔架进行疲劳寿命分析的具体过程如图 3所示.
|
| 图 3 预应力钢筋混凝土风电塔架疲劳寿命估算过程 Figure 3 Flowchart of fatigue life assessment of prestressed R.C. wind turbine towers |
计算模型为某风场200 kW风力发电机组的预应力钢筋混凝土塔架,截面为环形,高度为30 m,每10 m分为一个塔段,采用后张法施工工艺,预应力钢筋的分布按高度不同分别为12~24根,预应力随塔段由上至下逐渐增大,塔架采用200 MPa级活性粉末混凝土,预应力钢筋为fpk=1 860 MPa钢绞线.风力发电机组总重9.5t,有3个桨叶,额定工作转速为48 r/min.塔架参数如表 1所示.
| 塔架材料 | 塔架高度/m | 顶部外径/m | 底部外径/m | 叶轮直径/m | 预应力钢筋数/根 | 预应力/GPa | 分部厚度/mm |
| 预应力钢筋混凝土 | 30 | 1.7 | 3.2 | 37.5 | 12~24 | 1.12 | 205~250 |
使用ANSYS软件建立有限元分析模型.塔架混凝土部分采用Solid65单元模拟,普通钢筋采用Link8单元模拟,预应力钢筋的分布情况按高度不同分别为12~24根,采用Link8单元模拟,机舱、轮毂和风机叶片集合成一个集中质量点,用Mass21单元模拟,不考虑检修门对塔筒的影响.模型底部与地面刚接,相邻单元之间节点位移协调.采用线弹性钢筋混凝土本构模型,不考虑材料非线性和几何非线性,预应力钢筋混凝土塔架有限元模型和顶部连接如图 4、5所示.

|
| 图 4 预应力钢筋混凝土风力发电塔架模型 Figure 4 Model of prestressed of top of tower reinforced concrete wind turbine tower |

|
| 图 5 塔架顶部连接模型 Figure 5 Connection model of top of tower |
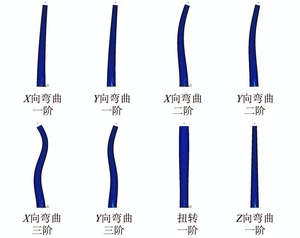
一般的风力发电塔架都会面临共振问题,即风机运行状态下的频率与塔架频率相等或接近,由文献[15]知,风机有3个浆叶,每转1周塔架受激振动3次.本文中风力发电机叶轮的转速范围为29~51 r/min,频率为0.483~0.85Hz,则作用在塔身上的轴向推力的频率为1.45~2.55 Hz.采用上述塔架模型进行模态分析,结果如表 2 和图 6所示.
| 模态阶数 | 固有频率/Hz | 模态性质 |
| 1 | 3.025 | X向弯曲一阶 |
| 2 | 3.025 | Y向弯曲一阶 |
| 3 | 13.564 | X向弯曲二阶 |
| 4 | 13.564 | Y向弯曲二阶 |
| 5 | 33.431 | X向弯曲三阶 |
| 6 | 33.431 | Y向弯曲三阶 |
| 7 | 39.366 | 扭转一阶 |
| 8 | 50.010 | Z向拉伸一阶 |
|
| 图 6 风电塔架振型(1~8阶) Figure 6 Mode shapes of wind turbine tower(1~8 th) |
由计算结果可见,由于未考虑塔架底部开洞情况,塔架的X、Y向质量分布和刚度分布相同,故塔架的X、Y向固有频率相同.计算得出的塔架频率均处于风机承受的轴向推力频率之外,因此该塔架避免了与叶片脉动激励的共振响应.
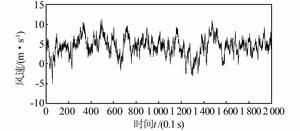
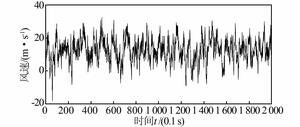
3.4 风荷载时程样本风荷载具有随机性,对于风电塔架而言,其风致疲劳分析需要计算出不同风速造成的损伤及其发生的概率.通常情况下,认为每个方向的平均风速均满足Weibull分布,采用文献[16]风速概率分布图,模拟出标准高度处平均风速分别为2、4、6、8、10和12 m/s的风荷载时程样本,图 7、8为模拟出的平均风速分别为4和12 m/s时的风荷载时程曲线.
|
| 图 7 平均风速4 m/s的风荷载时程样本 Figure 7 Time history of wind loading for average wind velocity of 4 m/s |
|
| 图 8 平均风速12 m/s的风荷载时程样本 Figure 8 Time history of wind loading for average wind velocity of 12 m/s |
对于预应力混凝土风力发电塔架而言,在无外荷载作用下时混凝土承受压应力,预应力钢筋承受拉应力且应力处于较高水平,故塔身受拉侧底端的预应力钢筋是极易发生疲劳的区域,因此文中对塔架受拉侧底端的预应力钢筋进行疲劳分析并由此进行风电塔架可靠性分析及疲劳寿命的预测.
采用雨流计数法统计出变幅应力谱后,根据损伤等效原则按下式将其折算为等效的常幅疲劳[17]:
式中:Δσe为变幅疲劳的等效应力幅;∑ni为以应力循环次数表示的结构预期使用寿命,在本文中取107;ni为预期寿命内应力幅水平达到Δσi的应力循环次数;β取3.5[18].
按图 3所示,对塔架受拉侧底端的预应力钢筋计算出在不同风速下的变幅应力谱进行等效折算,结果如表 3所示.
| 风速/(m·s-1) | 等效应力幅值/MPa | 实际循环次数 | 理论循环次数 | 损伤 |
| 2 | 1.559 6 | 5.07×108 | 1.46×1013 | 3.47×10-5 |
| 4 | 5.032 8 | 2.15×108 | 2.42×1011 | 8.87×10-4 |
| 6 | 12.331 3 | 9.61×107 | 1.05×1010 | 9.14×10-3 |
| 8 | 23.368 1 | 6.05×107 | 1.12×109 | 5.40×10-2 |
| 10 | 38.516 7 | 1.19×107 | 1.95×108 | 6.10×10-2 |
| 12 | 57.740 9 | 1.21×107 | 4.73×107 | 2.56×10-1 |
| 总计 | 3.81×10-1 | |||
表 3中,理论循环次数由计算得到的等效应力幅值再根据式(1)计算得出,实际循环次数按图 2编写的雨流计数法程序得出.塔架受拉侧底端的预应力钢筋初始应力为1 116.07 MPa,与N=107对应的应力幅为ΔσR=90 MPa,lgΔσR的SR=0.043.根据式(16)计算得
根据表 3计算可得Δσe常用对数lgΔσe的Se均值为0.067,按式(14)计算出塔架受拉侧底端预应力钢筋的疲劳可靠指标为
由式(15)计算得出相应的失效概率为
塔架的设计使用年限为20 a,由表 3中的疲劳损伤即可计算出预应力风电塔架T1,并预测出其剩余寿命T2:
通过上述的计算结果可以看出,塔架受拉侧底端的预应力钢筋的疲劳寿命>20 a,即整个塔架的疲劳关键点满足塔架设计使用年限为20 a的要求.
由表 3中的损伤结果中可以看出,塔架的疲劳关键点在平均风速为12 m/s下产生的疲劳损伤较大,这是因为随着风速的增加,塔架内预应力钢筋的应力水平相应增大,平均应力水平越高时,单位时间内产生的损伤增大,结构的疲劳寿命越低.
4 结论1) 塔架的前两阶固有频率在风机运行频率之外,故塔架所有频率均在安全频率范围之内,因此该预应力钢筋混凝土风电塔架的设计避免了叶片脉动激励的共振响应.但是随着风机塔架高度的升高,塔架的固有频率会逐渐降低,因此需要合理考虑荷载的共振响应.
2) 简化后的雨流计数法省去二次雨流时的对接,只需循环执行一次雨流即可,而且操作较传统雨流计数方便、快捷.
3) 经模拟和计算分析得出,塔架的疲劳可靠指标为2.92,塔架受拉侧底端的预应力钢筋的相应失效概率为0.18%.
4) 研究发现塔架疲劳寿命满足其设计使用年限的要求.塔架受拉侧底端的预应力钢筋为其疲劳分析时的关键点,本文未考虑门洞对塔架的影响,但在实际设计中需要进一步对门洞与塔架连接部位进行疲劳分析.门洞开设在背离常年主导风向一侧时对于塔架抗疲劳能力的提高较为有利.
5) 不考虑风向变化的概率时,在2~12 m/s风速段内,随着风速的增加,损伤程度相应增大,损伤累计的程度也越深.
| [1] | Petrov A A. Dynamic response and life prediction of steel structures under wind loading[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1998(98): 1057–1065. |
| [2] | Robertson A P, Holmes J D, Smith B W. Verification of closed-form solutions of fatigue life under along-wind loading[J]. Engineering Structures, 2004, 26(10): 1381–1387. DOI:10.1016/j.engstruct.2004.05.004 |
| [3] |
欧进萍, 叶骏. 结构风振的概率疲劳累积损伤[J].
振动工程学报, 1993(2): 164–169.
Ou Jinping, Ye Jun. Probabilistic fatigue cumulative damage of wind-resistance structures[J]. Journal of Vibration Engineering, 1993(2): 164–169. |
| [4] |
刘胜祥, 李德源, 黄小华. 风波联合作用下的风力机塔架疲劳特性分析[J].
太阳能学报, 2009, 10: 1250–1256.
Liu Shengxiang, Li Deyuan, Huang Xiaohua. Fatigue characteristic analysis of the offshore wind turbine tower under combinwid and wave[J]. Acta Energiae Solaris Sinica, 2009, 10: 1250–1256. |
| [5] |
王永玲. 风力发电机塔架优化设计与疲劳分析[D]. 大连:大连理工大学, 2012.
Wang Yongling. Optimization design and fatigue analysis for wind turbine tower[D]. Dalian: Dalian University of Technology, 2012. |
| [6] |
孙振. 建筑结构风荷载的计算机模拟与分析[D]. 南京:南京航空航天大学, 2007.
Sun Zhen. Computer simulation and analysis of wind loading of structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007 |
| [7] |
金伟良, 赵羽习. 混凝土结构耐久性研究的回顾与展望[J].
浙江大学学报(工学版), 2002(4): 27–36.
Jin Weiliang, Zhao Yuxi. State-of-the-art on durability of concrete structures[J]. Journal of Zhejiang University(Engineering Science), 2002(4): 27–36. |
| [8] |
李朝阳.钢筋混凝土结构的疲劳性能研究[D]. 大连:大连理工大学, 2001.
Li Chaoyang. Research on the fatigue performance of reinforced concrete structures[D]. Dalian: Dalian University of Technology, 2001. |
| [9] |
王世村. 高耸结构风振响应和风振疲劳研究[D]. 杭州:浙江大学, 2005.
Wang Shicun. Studies of wind-induced vibration and wind-induced fatigue on high-rise structures[D]. Hangzhou: Zhejiang University, 2005. |
| [10] |
马林. 国产1860级低松弛预应力钢绞线疲劳性能研究[J].
铁道标准设计, 2000(5): 21–23.
Ma Lin. Study on the fatigue performance of low relaxation prestressed steel strand for domestic 1860 type[J]. Railway Standard Design, 2000(5): 21–23. |
| [11] |
常大民, 江克斌.
桥梁结构可靠性分析与设计[M]. 北京: 中国铁道出版社, 1995.
Chang Damin, Jiang Kebin. The Reliability Analysis and Design of Bridge Structures[M]. Beijing: China Railway Publishing House, 1995. |
| [12] |
董乐义, 罗俊, 程礼. 雨流计数法及其在程序中的具体实现[J].
计算机技术与应用, 2004, 24(3): 38–40.
Dong Leyi, Luo Jun, Cheng Li. Rain flow count method and its realization in programming[J]. Computer Science and Application, 2004, 24(3): 38–40. |
| [13] |
过玉卿, 龙靖宇. 改进雨流计数法及其统计处理程序[J].
武汉钢铁学院学报, 1987(1): 22–28.
Guo Yuqing, Long Jingyu. An improved rain flow counting method and computer programming of its statistic treatment[J]. Journal of Wuhan Iron and Steel University, 1987(1): 22–28. |
| [14] |
毕继红, 陈花丽, 任洪鹏. 基于雨流计数法的接触线疲劳寿命分析[J].
铁道学报, 2012(6): 34–39.
Bi Jihong, Chen Huali, Ren Hongpeng. Analysis on fatigue life of contact wire based on rain-flow counting method[J]. Journal of the China Railway Society, 2012(6): 34–39. |
| [15] |
谢峰, 赵吉文, 沈维蕾, 等. 600 kW风力机塔架结构的仿真设计[J].
系统仿真学报, 2004(1): 70–72.
Xie Feng, Zhao Jiwen, Shen Weilei, et al. Simulating design of the tower structure for 600 kW-wind turbine[J]. Journal of System Simulation, 2004(1): 70–72. |
| [16] |
尹艳杰. 风力发电机塔架风荷载识别和风致疲劳的研究[D]. 呼和浩特:内蒙古科技大学, 2015.
Yin Yanjie. The study of wind load identification and wind-induced fatigue for wind turbine tower[D]. Inner Mongolia University of Science & Technology, 2015. |
| [17] |
GB 50017-2003钢结构设计规范[S]. 北京:中国计划出版社, 2003.
GB 50017-2003 Code of design of steel structure[S]. Beijing: China Architecture & Building Press, 2003. |
| [18] |
曹开胜. 钢筋混凝土桥梁疲劳损伤分析研究[D]. 大连:大连理工大学, 2012.
Cao Kaisheng. Fatigue damage analysis of thereinforced concrete bridge[D]. Dalian: Dalian University of Technology, 2012. |
 2016, Vol. 49
2016, Vol. 49




