文章信息
- 杜斐, 黄宏伟, 张东明, 张帆
- DU Fei, HUANG Hongwei, ZHANG Dongming, ZHANG Fan
- 上海轨道交通网络的复杂网络特性及鲁棒性研究
- Analysis of characteristics of complex network and robustness in Shanghai metro network
- 武汉大学学报(工学版), 2016, 49(5): 701-707
- Engineering Journal of Wuhan University, 2016, 49(5): 701-707
- http://dx.doi.org/10.14188/j.1671-8844.2016-05-010
-
文章历史
- 收稿日期: 2016-04-30
2. 同济大学地下建筑与工程系,上海 200092;
3. 必维国际检验集团,上海 200011
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;
3. Bureau Veritas, Shanghai 200011, China
轨道交通具有快捷、环保、舒适等优点,逐渐成为各城市用于缓解地面交通压力的措施.我国的上海、北京、广州等城市已建成一定规模的轨道交通网络.一方面,各城市的轨道交通网络仍在不断地发展演化;另一方面,轨道交通在网络化运营过程中,信号故障、恶意袭击等突发事件会导致站点或线路瘫痪,对轨道交通网络的安全运营造成不利的影响,进而造成经济损失与人员伤亡[1].
在此背景下对轨道交通网络的复杂网络特性进行研究能够从直观上认识网络的结构特征,给出网络发展演化的拓扑描述;而研究轨道交通网络对外界干扰破坏的抵抗能力,即网络的鲁棒性,对保障轨道交通安全运营具有重要的意义.轨道交通网络的复杂网络特性反映了网络的结构特征,而其鲁棒性则是网络功能的一部分[2],结构和功能正是复杂网络理论研究的两个核心问题[3],二者并非相互独立,而是存在着本质的相互联系,结构影响功能,功能反过来影响结构的发展演化[4].
国内外学者应用复杂网络理论对复杂网络的特性和鲁棒性进行了大量的研究.Watts和Strogatz[5]在研究复杂网络问题时提出了小世界网络模型;Barabási和Albert[6]提出了无标度网络模型;Latora和Marchiori[7]验证了波士顿地铁网络是小世界网络,并提出小世界网络是地铁网络的建造法则;韩继彬等[8]采用Space L方法对2012年的上海轨道交通网络特性进行了研究,其研究表明当时的上海轨道交通网络在L空间中是无标度网络但不是小世界网络.Albert等[9]与Crucitti等[10,11]的研究指出无标度网络对随机故障表现出鲁棒性,而对蓄意攻击表现出脆弱性.
有关上海轨道交通网络的研究[8, 12-14]多是针对网络的特性和可靠性分析,对于鲁棒性还缺少相关的研究.本文基于复杂网络理论,实证分析上海轨道交通网络的复杂网络特性,研究上海轨道交通网络的鲁棒性,研究成果可望为上海乃至国内其他城市轨道交通网络的日常维护、安全运营以及合理的规划与设计提供理论参考.
1 上海轨道交通网络特性分析 1.1 上海轨道交通网络拓扑结构的构建上海市的轨道交通建设起步较晚,但发展非常迅速,从1995年4月10日第一条轨道交通线路投入运营,截止到2015年12月31日已发展为包含15条运营线路(含磁浮线)、303个站点、总长度共计617 km(含磁浮线29 km)的庞大轨道交通网络.
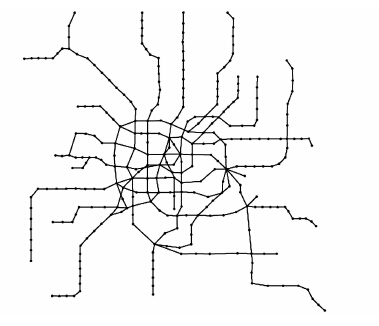
网络的拓扑结构是研究网络结构特征和功能的基础,轨道交通网络拓扑结构的构建主要有4种方法[15]:Space L法、Space P法、Space B法和Space C法,每种方法构建的拓扑结构中节点与线的含义见表 1.在4种方法中,由于Space L法建模直观,节点与线的含义及其相互连接与真实的轨道交通网络相近,故本文采用Space L方法构建上海轨道交通网络的拓扑结构,如图 1所示.
| 拓扑图 | 节点 | 线 |
| Space L | 站点 | 站点之间的线路,代表两个站点直接相连 |
| Space B | 站点和线路 | 代表站点隶属于某条线路 |
| Space P | 站点 | 代表一个站点到另外一个站点不需要换乘 |
| Space C | 线路 | 代表两线之间可直接换乘 |
|
| 图 1 上海轨道交通网络拓扑结构 Figure 1 Topology of Shanghai metro network |
对上海轨道交通网络拓扑结构作以下说明:
1) 选用截止到2015年12月31日上海轨道交通网络站点及线路数量的数据,未考虑只有首末两个站点的磁悬浮线以及规划在建的线路,共14条运营线路,303个站点.
2) 针对部分线路有重叠站点的情况,如3号线与4号线部分线路有重叠站点,认为是同一个站点有多条线路通过,但将两座浦电路站视为两个不同的站点.
3) 不考虑轨道交通网络中上下行线路、车辆运行时间、发车频次和载客流量以及政治文化等因素,节点之间有直接连接则连接强度为固定值1,无直接连接则为无穷大,即本文所研究的上海轨道交通网络为无向非加权网络.
1.2 复杂网络特征指标计算及分析在L空间中,典型的复杂网络特征指标包括:节点数、边数、节点度及度分布、网络的平均度、平均路径长度、网络直径和聚类系数等[3],这些指标分别描述了复杂网络不同方面的特征,综合起来能够比较全面地反映网络的特征.
根据图 1可建立上海轨道交通网络的邻接矩阵{aij},该邻接矩阵为303×303的对称矩阵,在矩阵中,1表示两个站点是直接相连的,0表示同一个站点,100表示两个站点不直接相连.利用Excel软件可计算得到网络的节点数、边数及平均度;利用Matlab软件根据Floyd算法[16]可得到轨道交通网络节点间的距离矩阵,进一步利用相应的算法计算可得到其他特征指标.上海轨道交通网络的复杂网络特征指标计算结果如表 2所示.
| 特征指标 | 计算值 |
| 节点 | 303 |
| 边数 | 350 |
| 平均度 | 2.31 |
| 平均路径长度 | 14.87 |
| 网络直径 | 41 |
由表 2的计算结果可得,上海轨道交通网络拓扑结构中的节点数为303,边数为350,表示上海轨道交通运营网络共有303个站点,350段区间线路;平均度为2.31表示在上海轨道交通网络中平均1个站点与2.31个其他站点直接相连;平均路径长度为14.87表示在上海轨道交通网络中平均最短路程要经过14.87个站点;网络直径为41表示上海轨道交通最长的一条线路要经过41个站点.
1.3 复杂网络特性分析Watts和Strogatz[5]指出小世界网络具有与随机网络一样短的平均路径长度,又有像规则网络一样的高聚集度.小世界网络要符合以下两个条件[5]:
式中:LRandom为随机网络的平均路径长度;CRandom为随机网络的聚类系数;N为网络中节点总数;<k>为网络的平均度.
为验证上海轨道交通网络在L空间中是否为小世界网络,本文根据式(1)、(2)求得与上海轨道交通网络同规模的随机网络的平均路径长度与聚类系数,计算结果见表 3.同规模是指两个网络具有相同的节点数、边数和平均度.
| 特征指标 | 上海轨道交通网络 | 随机网络 |
| 平均路径长度 | 14.87 | 6.82 |
| 网络聚类系数 | 0.008 2 | 0.007 6 |
由表 3可知,相比于同等规模的随机网络,上海轨道交通网络的平均路径长度大于随机网络的平均路径长度,网络聚类系数也大于随机网络的聚类系数,因此在L空间中上海轨道交通网络是小世界网络.结合Milgram[17]的研究结果,该结论表示尽管实际的上海轨道交通网络规模很大,但任意两站点之间有相对较短的路径,各个站点之间连通流畅,整个网络系统的运行质量较好.
Barabási和Albert[6]提出的无标度网络的特点是在网络中很少的节点具有较大的度,而有很多的节点具有较小的度,网络节点的累积度分布P(k)服从幂律分布,即
式中:p(i)为节点度为i的节点占总节点数的比例;kmax为网络中节点度的最大值;γ为幂律指数,无标度网络的幂律指数一般为2.1~4.
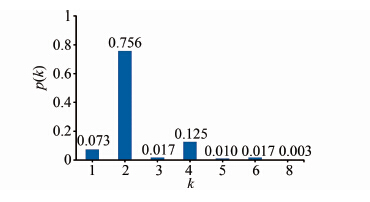
为验证上海轨道交通网络在L空间中是否为无标度网络,对网络中节点的度分布p(k)和累积度分布P(k)进行统计分析.首先分析网络节点度的分布特征,如图 2所示为上海轨道交通网络的节点度分布.
|
| 图 2 上海轨道交通网络节点的度分布 Figure 2 Node degree distribution of Shanghai metro network |
在地铁网络中,节点的度数表示站点直接连接的区间线路或其他站点的数量,度数为1的节点代表的是某条线路的终点站,度数为2的节点代表只有一条线路通过的站点,而度数>2的节点代表的是换乘站.由图 2可知,在上海轨道交通网络中度数为2的站点占站点总数的75.6%,表明在上海轨道交通网络中有229个站点只有一条地铁线路通过;度数大于2的站点占站点总数的17.2%,表明上海轨道交通网络中有52座换乘车站,换乘站点的数量有待进一步的增加.
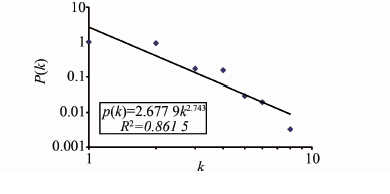
为获得节点累积度分布的分布形式,将上海轨道交通网络中的节点度及累积度分布的数据在双对数坐标系中进行拟合,拟合结果如图 3所示.
|
| 图 3 上海轨道交通网络双对数坐标累积度分布 拟合曲线 Figure 3 Fitting curve of cumulative degree distribution of Shanghai metro network in log-log plot |
由图 3可知,上海轨道交通网络的累积度分布服从幂律分布,幂律指数γ=2.743,位于[2.1,4]之间,拟合系数R2=0.861 5,拟合效果较好,上海轨道交通网络在L空间中是无标度网络.结合Albert等[9] 与Crucitti等[10-11]对无标度网络鲁棒性的研究成果,利用此结论可从网络结构特征的角度定性地判断上海轨道交通网络的鲁棒性:对随机故障表现出鲁棒性,而对蓄意攻击表现出脆弱性.但仅依据网络结构特征从定性的角度去认识网络的鲁棒性并不能为保护现有网络和改善网络性能提供可靠的理论依据,故本文第2章将从定量的角度分析上海轨道交通网络的鲁棒性.
1.4 不同时期上海轨道交通网络对比分析经上述分析,“上海城市轨道交通基本网络”在L空间中表现出小世界网络与无标度网络的特性,而根据韩继斌等[8]的研究,2012年的上海轨道交通网络在L空间中还不具有小世界网络的特性.为展现上海轨道交通网络近几年的发展情况,分析上海轨道交通网络特性变化的原因,本文对2015年12月与2012年8月的上海轨道交通网络进行对比分析,表 4分别列出了两个时期上海轨道交通网络参数.
由表 4可知,在2012年8月至2015年12月期间,随着上海地铁11号线北段二期、花桥段、迪士尼段,12号线全线,13号线一期、二期的投入运营,上海轨道交通网络的站点增加61座,增加25.2%;区间线路增加83条,增加31.1%;节点平均度增大0.1,说明上海地铁网络站点之间的联系有所增强;网络直径没有变化,均为41,网络规模的扩大并未改变网络中的最长线路;平均路径长度由于网络规模的扩大、站点数量的增加而增大0.08;网络的聚类系数由0.002增大到0.008 2,增大了4.1倍,这是由于新线路的投入运营,使部分站点之间由原来的不直接相连而变成直接相连,如大木桥路站与龙华中路站、金沙江路站与隆德路站,各站点之间的相互连接更加紧密,而聚类系数的增大使得上海轨道交通网络成为小世界网络.
2 上海轨道交通网络鲁棒性分析 2.1 轨道交通网络的鲁棒性及评价指标网络的鲁棒性是指当网络中的节点或边被破坏时,网络仍然能够继续维持其功能的能力[18].本文研究的轨道交通网络的鲁棒性指网络连通鲁棒性[19,20],即轨道交通网络遭受随机故障或蓄意攻击时,整个网络仍能保持连通的能力.
在复杂网络理论的基础上,交通网络鲁棒性的评价指标主要有:平均路径长度、网络最大子图大小和网络的全局效率[8].Latora和Marchiori[21]提出的网络全局效率[5]能够衡量网络的连通性,网络中节点i和j之间的效率εij可以用节点i和j两点之间的最短距离dij的倒数表示,即εij=1/dij,当节点i与j不连通的时候,dij等于无穷大,εij等于0.对于整个网络而言,将所有节点对之间效率的平均值定义为网络的全局效率,用Eglob表示,即
式中:N为网络中节点的数量;Eglob的取值范围是(0,1],当Eglob=1时,网络中任意两节点都是直接相连的,网络的连通性最好.
当网络遭受内部随机故障或外部蓄意攻击时,网络中受到攻击的节点会失效,有效节点的数目减少,全局效率也随之减小,新的网络全局效率为E′glob,计算公式为
式中:N′是网络遭受破坏后节点数量;d′ij是新的网络中节点i和j之间的最短路径.
网络的全局效率下降表示网络连通性降低,因此网络的鲁棒性就能用网络全局效率的变化值来表示.本文将网络全局效率作归一化处理,即采用网络全局效率的相对值rEglob作为轨道交通网络连通鲁棒性的评价指标,即
网络的鲁棒性主要包括网络面对随机故障和蓄意攻击时的鲁棒性[9-11].随机故障是指自然灾害、电力机械故障、信号故障等,对网络中所有节点来说随机故障发生的概率是相等的.蓄意攻击则包括人为恶意的纵火、恐怖袭击等有目的性的破坏行为,蓄意攻击主要针对的是一些重要的换乘站点.
针对复杂网络,在网络中随机删去节点表示随机故障的作用,而在网络中特意删去重要的节点表示蓄意攻击的作用.对于上海轨道交通网络,本文拟依次删去15个节点,约占总节点数的5%,随机故障和蓄意攻击的作用均是每次删去一个节点,直至删掉15个节点,随机故障是随机选择并删去节点(借助Excel生成随机数而选择节点删去),而蓄意攻击则是从高到低依次删去度数较大的节点.
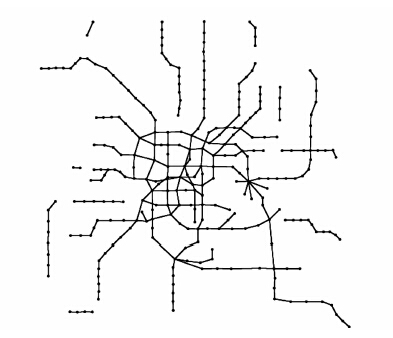
2.3 上海轨道交通网络的鲁棒性在模拟随机故障和蓄意攻击两种情况下,上海轨道交通网络在删去15个节点后的拓扑图如图 4、5所示.
|
| 图 4 随机故障后的上海轨道交通网络拓扑图 Figure 4 Topology of Shanghai metro network after random attacks |
|
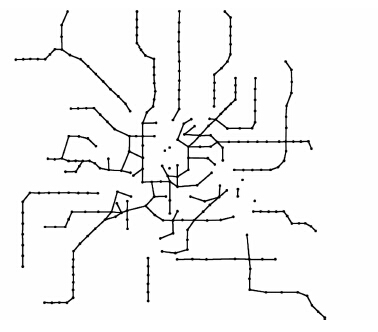
| 图 5 蓄意攻击后的上海轨道交通网络拓扑图 Figure 5 Topology of Shanghai metro network after malicious attacks |
由图 4、5可以直观地看出,上海轨道交通网络5%的节点在遭遇随机故障后,整个网络仍具有一定的完整性,轨道交通运营仍能保证一定的网络化,但是网络在遭遇蓄意攻击后,5%的节点失效使整个网络变得支离破碎.
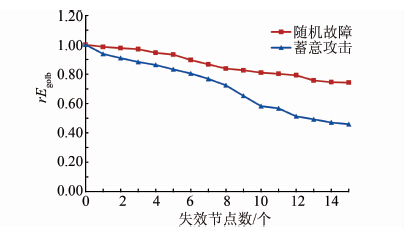
按照前文提出的网络鲁棒性指标及节点失效策略,通过计算可以得到上海轨道交通网络分别在随机故障、蓄意攻击发生时的网络全局效率的相对值rEglob的变化曲线如图 6所示,由图可知,上海轨道交通网络在面对随机故障时,网络全局效率下降比较平缓,而受到蓄意攻击时,网络全局效率下降迅速.
|
| 图 6 上海轨道交通网络全局效率相对值变化曲线 Figure 6 The changing curve of Shanghai metro network relative global efficiency |
当轨道交通网络遭遇随机故障时,15个节点失效造成网络全局效率下降25.7%,单个节点失效造成网络全局效率下降平均值为1.71%,即在上海轨道交通网络中,当有5%的站点发生随机故障而失效时,网络全局效率为无站点失效时网络全局效率的74.3%.由此可见,上海轨道交通网络对随机故障有较好的鲁棒性,15个站点失效后轨道交通网络的连通性仅下降25.7%,这是因为在上海轨道交通网络中,度数为2的节点占绝大多数(比例为75.6%),在随机选择失效节点时,度数为2的节点被选中的概率是最大的,而度数为2的节点失效对网络全局效率的影响有限.
当轨道交通网络遭遇蓄意攻击时,15个节点失效造成网络全局效率下降54.1%,单个节点失效造成网络全局效率下降平均值为3.61%,为遭遇随机故障时的2.1倍,当有5%的站点发生失效时,网络全局效率仅为无节点失效时网络全局效率的45.9%.由此可见,上海轨道交通网络对蓄意攻击的鲁棒性较差,15个站点在遭受蓄意攻击而失效后轨道交通网络的连通性下降45.9%,这是因为蓄意攻击针对的是度数大的节点,而每个度数大的节点失效会造成多条通过节点的线路随之失效,对网络的连通性造成较大的打击.
由上述分析可知,上海轨道交通网络对随机故障鲁棒,而面对蓄意攻击表现出脆弱性,这符合无标度网络鲁棒性的特征.造成这种情况的原因是在蓄意攻击下失效的节点都是度数比较大的节点,把节点删去的同时也把其所连接的边一同删去,所以会直接加大网络中任意两节点之间的最短距离,甚至会出现最短距离无限大即不能连通的情况,从而使全局效率大大降低.
为研究单个节点失效对网络全局效率Eglob的影响,本文分别计算了图 5中上海地铁网络遭遇蓄意攻击而失效的15个节点单独失效时Eglob的变化值ΔEglob,计算结果如表 5所示.
| 失效节点 | Eglob | ΔEglob/% | k | |
| 1 | 曹杨路 | 0.092 1 | 7.37 | 4 |
| 2 | 上海火车站 | 0.092 8 | 6.69 | 4 |
| 3 | 龙阳路 | 0.093 2 | 6.24 | 5 |
| 4 | 宜山路 | 0.093 2 | 6.22 | 5 |
| 5 | 世纪大道 | 0.093 2 | 6.22 | 8 |
| 6 | 虹口足球场 | 0.094 2 | 5.18 | 4 |
| 7 | 东方体育中心 | 0.095 0 | 4.46 | 5 |
| 8 | 中山公园 | 0.097 2 | 2.19 | 4 |
| 9 | 南京西路 | 0.097 3 | 2.10 | 6 |
| 10 | 汉中路 | 0.097 5 | 1.95 | 6 |
| 11 | 徐家汇 | 0.097 6 | 1.79 | 6 |
| 12 | 西藏南路 | 0.097 7 | 1.71 | 4 |
| 13 | 人民广场 | 0.097 9 | 1.54 | 6 |
| 14 | 陕西南路 | 0.097 9 | 1.54 | 6 |
| 15 | 东安路 | 0.098 4 | 1.00 | 4 |
由表 5可知,曹杨路、上海火车站、龙阳路、宜山路、世纪大道等站点失效时,对上海轨道交通网络的全局效率影响较大,这5个节点单独失效时网络全局效率下降超过6%.曹杨路站点失效时,网络的全局效率下降幅度最大,为7.37%.表 5同时列出了节点度k的值,通过对比可发现单个节点失效对网络全局效率的影响与节点度数不呈现严格的正相关关系[22].节点度数最大的世纪大道站失效造成网络全局效率下降6.22%,且度数为6的几个节点的失效造成网络全局效率下降值均不超过2.1%,而度数为4的曹杨路站失效造成网络全局效率下降7.37%,度数为4的上海火车站失效造成网络全局效率下降6.69%,造成这种现象的原因为曹杨路站、上海火车站是分别连接11号线支线、1号线支线与中心网络的节点,这两个节点的失效会造成大量节点与中心网络分离,使网络效率下降而大大降低网络的连通性,宜山路、虹口足球场等站点也具有相似的特点;而陕西南路、人民广场等站点,其周围站点比较密集,网络的容错性较好,该节点失效后,周围站点可以起到一定的疏通作用,虽然其失效会造成网络连通性下降,但不会产生大量的与网络不相连的孤立节点,故其对网络连通性的影响有限.
综上所述,在轨道交通网络日常运营及规划建设中,要加强对节点度数较高的站点(如世纪大道站、人民广场站等)以及连接支线与中心网络的站点(如曹杨路站、上海火车站)的日常维护与安全防护,避免此类重要站点发生故障或遭受蓄意攻击而对整个轨道交通网络的连通性造成较大的影响.
3 结论本文基于复杂网络理论,采用Space L方法构建了“上海城市轨道交通基本网络”的拓扑结构,实证分析了上海轨道交通网络的网络特征指标及复杂网络特性,定量研究了上海轨道交通网络面对随机故障和蓄意攻击时的鲁棒性,得出以下结论:
1) 截止2015年12月31日,上海城市轨道交通基本网络中75.6%的站点与另外两个站点直接相连,平均1个站点与2.31个其他站点直接相连,平均最短路程要经过14.87个站点,最长的一条路线要经过41个站点.
2) 通过对网络特征值的实证分析得出上海轨道交通网络在L空间中的结构特征,即小世界网络、无标度网络.通过网络的结构特征可判断当前网络的整体运行情况以及网络对外界干扰破坏的抵抗能力,小世界网络表明当前上海轨道交通网络整体运行质量较好,而且随着网络的不断发展演化,网络规模越来越大,各站点之间的联系越来越紧密,网络运行会更加通畅;无标度网络表明当前上海轨道交通网络对随机故障具有较强的抵抗能力,但对蓄意攻击抵抗力较差.
3) 上海轨道交通网络在面对站点遭遇随机故障时有较强的鲁棒性,而对于以最大度为目标进行的站点蓄意攻击,网络表现出脆弱性,这一结论的现实意义是要加强对节点度数较高的站点与连接支线以及中心网络站点的日常维护与安全防护,保障其正常运行,防止因其失效而造成网络瘫痪.
| [1] |
黄宏伟, 叶永峰, 胡群芳. 地铁运营安全风险管理现状分析[J].
中国安全科学学报, 2008(07): 55–62.
Huang Hongwei, Ye Yongfeng, Hu Qunfang. Analysis of the current situation of metro operation safety risk management[J]. China Safety Science Journal, 2008(07): 55–62. |
| [2] |
李春光. 复杂网络建模及其动力学性质的若干研究[D]. 成都: 电子科技大学, 2004.
Li Chunguang. Modeling and dynamic properties of complex networks[D]. Chengdu: University of Electronic Science and Technology of China, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10183-2009092001.htm |
| [3] |
方爱丽, 赵继军. 复杂网络:结构和动力学[J].
复杂系统与复杂性科学, 2006, 3(3): 56–94.
Fang Aili, Zhao Jijun. Complex networks: structure and dynamics[J]. Complex Systems and Complexity Science, 2006, 3(3): 56–94. |
| [4] |
吴建军. 城市交通网络拓扑结构复杂性研究[D]. 北京:北京交通大学, 2008.
Wu Jianjun. Studies on the complexity of topology structure in the urban traffic network[D]. Beijing: Beijing Jiaotong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10004-2009069010.htm |
| [5] | Watts D J, Strogatz S H. Collective dynamics of 'small-world' networks[J]. Nature (London), 1998, 393: 440–442. DOI:10.1038/30918 |
| [6] | Barabvasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286: 509–512. DOI:10.1126/science.286.5439.509 |
| [7] | Latora V, Marchiori M. Is Boston subway a small-world network?[J]. Physical A, 2002, 314: 109–113. DOI:10.1016/S0378-4371(02)01089-0 |
| [8] |
韩纪彬, 郭进利, 张新波. 上海市轨道交通网络可靠性研究[J].
中国安全科学学报, 2012(12): 103–108.
Han Jibin, Guo Jinli, Zhang Xinbo. Reliability analysis of Shanghai rail transit network[J]. China Safety Science Journal, 2012(12): 103–108. |
| [9] | Albert R, Jeong H, Barabvasi A L. Error and attack to lerance of complex networks[J]. Nature, 2000, 406: 378–382. DOI:10.1038/35019019 |
| [10] | Crucitti P, Latora V, Marchiori M, et al. Efficiency of scale-free networks: error and attack tolerance[J]. Physical A, 2003, 320: 622–642. DOI:10.1016/S0378-4371(02)01545-5 |
| [11] | Crucitti P, Latora V, Marchiori M, et al. Error and attacktolerance of complex networks[J]. Physical A, 2004, 340: 388–394. DOI:10.1016/j.physa.2004.04.031 |
| [12] |
王燚, 杨超. 上海市轨道交通网络的复杂网络特性研究[J].
城市轨道交通研究, 2009(2): 33–36.
Wang Yi, Yang Chao. Characteristics of the complex network in Shanghai urban rail transit[J]. Urban Mass Transit, 2009(2): 33–36. |
| [13] |
慈立坤, 胡蒙达. 上海城市轨道交通网络运营可靠性研究[J].
城市轨道交通研究, 2009, 12(4): 41–44.
Ci Likun, Hu Mengda. Reliability of Shanghai urban rail transit networking operation[J]. Urban Mass Transit, 2009, 12(4): 41–44. |
| [14] |
丁小兵. 复杂网络理论及其在上海城市轨道交通网络可靠性分析评价中的应用[J].
城市轨道交通研究, 2012, 11: 50–53.
Ding Xiaobing. Complex network theory and application in reliability of Shanghai urban rail transit network[J]. Urban Mass Transit, 2012, 11: 50–53. |
| [15] | Ferber C, Holovatch T, et al. Public transport networks: empirical analysis and modeling[J]. The European Physical Journal B, 2009, 68: 261–275. DOI:10.1140/epjb/e2009-00090-x |
| [16] |
周炳生. Floyd算法的一个通用程序及在图论中的应用[J].
杭州应用工程技术学院学报, 1999(3): 1–9.
Zhou Bingsheng. A general program of Floyd's algorithm and its application in graph theory[J]. Hangzhou Institute Applied Engineering, 1999(3): 1–9. |
| [17] | Milgram S. The small world problem[J]. Psychology Today, 1967, 1: 60–67. |
| [18] |
熊海文, 赵继军. 复杂网络:结构和动力学[J].
复杂系统与复杂性科学, 2006, 3(3): 52–90.
Xiong Haiwen, Zhao Jijun. Complex networks: structure and dynamics[J]. Complex Systems and Complexity Science, 2006, 3(3): 52–90. |
| [19] |
杜巍, 蔡萌, 杜海峰. 网络结构鲁棒性指标及应用研究[J].
西安交通大学学报, 2010(4): 93–97.
Du Wei, Cai Meng, Du Haifeng. The indicators and application of network structure robustness[J]. Journal of Xi'an Jiaotong University, 2010(4): 93–97. |
| [20] |
王志如, 李启明, 梁作论. 城市轨道交通网络拓扑结构脆弱性评价[J].
中国安全科学学报, 2013(08): 114–119.
Wang Zhiru, Li Qiming, Liang Zuolun. Evaluation of urban metro network topological structure vulnerability[J]. China Safety Science Journal, 2013(08): 114–119. |
| [21] | Latora V, Marchiori M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 87(19): 198701. DOI:10.1103/PhysRevLett.87.198701 |
| [22] | Latora V, Marchiori M. How the science of complex networks can help developing strategies against terrorism[J]. Chaos Solitions & Fractals, 2004, 20(1): 69–75. |
 2016, Vol. 49
2016, Vol. 49



