文章信息
- 李俊益, 陈启卷
- LI Junyi, CHEN Qijuan
- 水轮机调节系统Hopf分岔分析及其PID控制
- Hopf bifurcation analysis of hydroturbine regulating system and its PID control
- 武汉大学学报(工学版), 2018, 51(5): 451-458,470
- Engineering Journal of Wuhan University, 2018, 51(5): 451-458,470
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-013
-
文章历史
- 收稿日期: 2016-11-25
2. 武汉第二船舶设计研究所,湖北 武汉 430060
2. Second Ship Research Insitute of Wuhan, Wuhan 430060, China
Hopf分岔是非线性动力系统中相对比较简单而又重要的分岔问题,属于一种局部动态分岔[1, 2],随着分岔参数的变化,系统在非双曲平衡点处从平衡点突然分岔出极限环.对于非线性系统Hopf分岔的研究,一般需要解决如下3个方面的问题:1)Hopf分岔的存在性,即系统是否存在周期解,这是Hopf分岔研究中需要解决的基本问题;2)Hopf分岔的方向,即出现分岔的参数范围;3)Hopf分岔的稳定性,即存在周期解时,其稳定性如何(超临界或亚临界).
Hopf分岔问题的提出及其理论研究均具有深刻的应用背景[3-6],它通常与系统自激振荡有密切联系.如在水轮机非线性系统中,即使无任何外部激励,也可能会出现某一固定频率和振幅的自激振荡,还有可能出现频率和振幅不相同的自激振荡,甚至出现更复杂的非线性振荡以至于混沌现象[7].然而,到目前为止,对水轮机调节系统中可能存在的分岔与振荡问题却一直研究较少,水轮机调节系统中存在着复杂分岔现象也是理论工作者和工程技术人员所关心的问题.对水轮机调节系统而言,分岔现象是一种严重的失稳现象,通常与系统的自激振荡有密切联系,因此,在控制系统设计中必须给予足够的重视[8-9].
双Hopf是一类非常重要的余维Hopf分岔现象,此时,从平衡点分岔出来的不再是周期轨道,而可能是拟(准)周期轨道,在适当选取的三维相空间中形成轮胎面或指环形的吸引域.文献[10-13]运用多尺度方法计算系统的规范形,借助相关计算软件,对一些较典型的机械及电路系统中的双Hopf分岔进行了分析计算.但针对水轮机调节系统的双Hopf分岔分析研究却很少,因此,揭示水轮机调节系统中存在的双Hopf分岔现象和发生机理很有意义.
鉴于此,本文首先给出水轮机调节系统刚性水击和弹性水击时对应的四维和六维模型,并说明了系统Hopf存在的条件及分岔方向的计算,再根据系统特征多项式系数推导出双Hopf分岔存在的判别和计算方法,最后通过仿真和数值计算对理论分析进行验证.
1 Hopf分岔存在性判定定理1:考虑Ck(k≥0)向量场f:U×V∈Rn上的含参数的非线性动力系统:
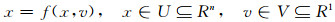
其中,v为系统的参数,称为分岔参数或控制变量.设向量场f∈C2,(x0,v0)∈U×V是平衡点,若下列条件成立,则在平衡点(x0,v0)处出现极限环:
1) f(x0,v0)=0;
2) Dfx(x0,v0)有一对纯虚特征值λ(v0)=±iω0,其余n-2个特征根的实部均不为0;
3) a′(v0)=d/dvReλ(v0)≠0.
定理1称为Hopf分岔定理,条件2表明Hopf分岔点是非双曲平衡点,Hopf分岔现象发生在一对共轭特征值穿越虚轴时,常用于作Hopf分岔现象的判据;条件3称为横截系数,主要用于判断Hopf分岔的方向.
但定理1并未给出Hopf分岔的稳定性判定,因此需要进一步计算与Hopf分岔方向及稳定性相关的特征量.一般来说,Hopf分岔存在性问题只需要用到原非线性系统线性化部分的信息,而稳定性问题的解决则需要用到非线性部分的信息,与存在性问题相比,稳定性问题更为复杂,从本质上讲其原因在于存在性问题仅涉及到解的拓扑结构,而稳定性问题则与解的度量性质有关,将会涉及到更复杂的计算.
描述Hopf分岔方向及稳定性的特征量一般包括:1)系统Jacobi矩阵特征值实部的导数a′(v0),即横截系数;2)曲率系数β值.根据分岔的横截系数(或规范形系数)和曲率系数可将Hopf分岔分为超临界和亚临界两种,超临界Hopf分岔对应于稳定的振荡或系统状态相空间中的稳定极限环;而亚临界Hopf分岔对应于不稳定的振荡或系统状态相空间中的不稳定极限环,将对系统的稳定运行产生不利的影响.
横截系数a′(v0)和曲率系数β与Hopf分岔的稳定性及分岔方向之间的关系可归结为下述定理.
定理2[14]:当系统存在Hopf分岔,若β < 0,表明系统发生超临界的Hopf分岔,系统的周期解是稳定的;当a′(v0)>0,稳定的极限环出现在v0>0一侧,而在v0 < 0的一侧系统是渐近稳定的;而当a′(v0) < 0,极限环出现在v0 < 0一侧,在v0>0的一侧系统是渐近稳定的.若β>0,则表明系统的Hopf分岔是亚临界的;a′(v0)>0时,极限环出现在v0 < 0一侧充分小的邻域内,a′(v0) < 0时,极限环出现在v0>0一侧充分小的邻域内.
由定理1,当系统中存在非双曲平衡点,且其Jacobi矩阵中出现一对纯虚特征值,其余特征值均有负实部时,则系统发生Hopf分岔.而在四维及四维以上的系统中,当Jacobi矩阵出现多对纯虚特征值时,则系统发生的是多Hopf分岔,其中以双Hopf分岔(Hopf-Hopf分岔)较为常见,即两对复共轭特征值同时穿越虚轴的现象,其判别方法在后文中根据具体系统将详细介绍.如图 1(a)所示为两对复共轭特征值同时从复平面左半侧进入右半平面的情况,表明此时系统从稳定状态通过分岔失稳;图 1(b)为两对复共轭特征值中的一对从复平面左半侧进入右半平面的同时,另一对复共轭特征值从复平面右半侧进入左半平面,表明系统在经历双Hopf分岔前后均处于不稳定状态.
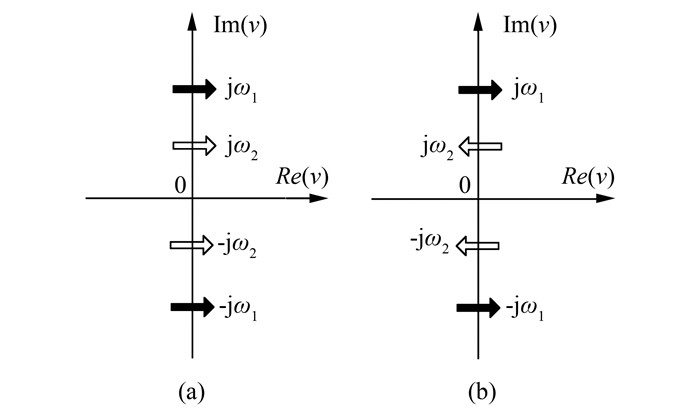
|
| 图 1 双Hopf分岔 Figure 1 Double Hopf bifurcation |
对于一般的非线性系统,特别是维数较高时,直接应用定理1来判断Hopf分岔的存在性并不方便.实践中需要更直接的方法用于Hopf分岔存在性的判断.对于四维非线性系统,定理3给出了系统存在Hopf分岔的条件,并可同时计算出发生Hopf分岔时系统分岔值.
定理3:非线性系统y=f(x, v)中,x∈R4,v∈R1为分岔参数,x=0为系统的平衡点,在平衡点时的系统Jacobi矩阵特征多项式可表示为
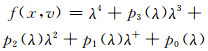 (1)
(1)
若当v=0时,以下各条件成立:
1) 系数pi>0(i=0, 1, 2, 3),且满足:
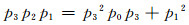 (2)
(2)
2) 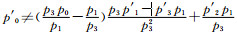
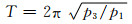 (3)
(3)
定理3是判断四维系统存在Hopf分岔的直接代数判据[9],应用该定理可避免过多烦琐的计算.由条件1所决定的曲面上各点就是发生Hopf分岔现象的分岔临界点.当系统在某工况下的参数满足条件1和2时,将出现周期振荡的失稳现象,即Hopf分岔现象,同时,该曲面也确定了系统的稳定域.从非线性动力系统结构稳定性分析的角度而言,当系统参数满足一定条件时,其结构稳定性会发生突变,出现系统结构失稳现象,从而导致系统表现出复杂非线性振荡行为.
对于四维系统,当发生双Hopf分岔时,其Jacobi矩阵可变换成如下形式:
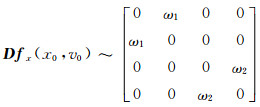
其相应的特征方程:
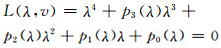 (4)
(4)
应具有如下形式:
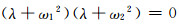 (5)
(5)
ω1>0、ω2>0为两对纯虚特征值的虚部,令式(4)和(5)中特征值λ对应的阶次系数相等,可得到四维非线性动力系统中发生双Hopf分岔时应满足的必要条件.
定理4:非线性系统y=f(x, v)中,x∈R4,v∈R1为分岔参数,x=0为系统的平衡点,在平衡点时的系统Jacobi矩阵特征多项式为式(1),若
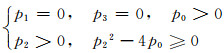 (6)
(6)
成立,则当分岔参数v=0时,系统出现双Hopf分岔现象,且两个振荡频率ω1和ω2由下式获得:
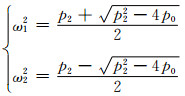 (7)
(7)
当ω1/ω2为无理数时,双Hopf分岔称为非共振的,否则称为共振的,式(7)中,若p22-4p0=0,则ω1:ω2=1:1,此时系统将出现1:1共振双Hopf分岔.
1.2 六维水轮机调节系统对于四维以上的非线性系统,应采用下列定理.
定理5:非线性系统y=f(x, v)中,x∈Rn,v∈R1为分岔参数,x=0为系统的平衡点,在平衡点时的系统Jacobi矩阵特征多项式为
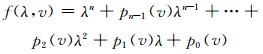 (8)
(8)
若当v=v0时,有
1) Δi>0(i=1,2,…,n-2),Δn-1=0,p0(v0)>0;
2) ω02UZ≠VW.
Δi(i=1,2,…,n)是由式(8)的系数所构造的Hurwitz行列式:
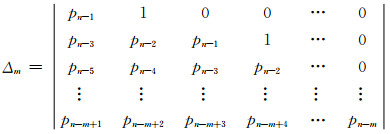
m=1, 2,…,n;若i>n,则pn-1=0
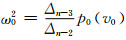 (9)
(9)
n为偶数时:
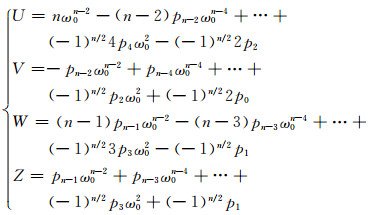
n为奇数时:
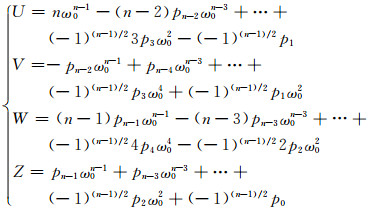
当|v-v0|充分小时,系统在v0的某一侧存在Hopf分岔,定理6则进一步给出了判断高维非线性动力系统发生Hopf分岔的必要条件.
定理6:特征方程(8)有一对纯虚特征值,而其余n-2个特征值均具有负实部的充分必要条件是:
1) pi>0(i=0,1,2,…,n-1);
2) Δn-1=0,Δi>0(i=n-3,n-3,…).
定理5和6是判断非线性动力系统Hopf分岔存在性直接代数判据,通常用于维数较高的非线性系统.定理6条件2只要求一半Hurwitz行列式大于0,故其所涉及到的计算量小于定理5,因而实际应用更为简便.当满足定理6的两个条件时,非线性动力系统成为实际应用中常见的半单系统.由于分岔点是系统状态稳定的临界点,因此,分岔点的位置将决定系统在参数空间中的稳定域及稳定裕度.
对于六维系统,发生双Hopf分岔时,其Jacobi矩阵可变换为
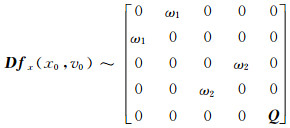
其中,Q∈R2.系统相应的特征方程:
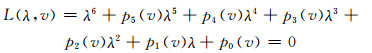 (10)
(10)
应具有如下形式:
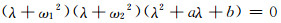 (11)
(11)
式中,ω1>0,ω2>0为两对纯虚特征值的虚部,方程λ2+aλ+b=0的两个根为矩阵Q的特征值.令式(10)、(11)中特征值λ的同阶次系数相等,可得到代数方程组:
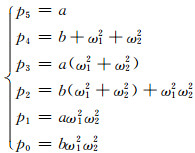 (12)
(12)
若控制系统采用PID控制,则在系统特征方程系数pi中,除ω1、ω2、a、b四个未知量外,还包括3个PID参数;应用中,根据先验知识或仿真结果,先确定其中一个控制参数,再通过方程组(12)计算出其余6个未知量.考虑到方程组(12)可能存在多解,实际计算中需将数值解代入到原方程组以获得稳态解,并计算系统Jacobi矩阵特征值进行验证.因此,式(12)可作为六维非线性系统双Hopf分岔的必要条件,用于水轮机调节系统六维非线性模型双Hopf分岔现象的研究.
2 数值计算与仿真 2.1 四维非线性系统模型考虑发电机转子二阶动态模型和当前在水轮机调节系统中常用的PID控制,并结合文献[14, 15]中提出的刚性水击时的水轮机调节系统非线性模型,给出其四维非线性方程组:
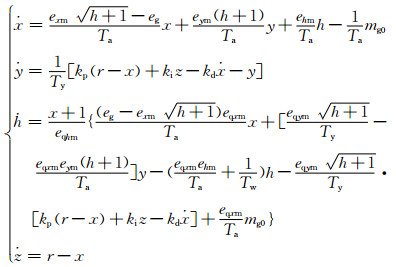
其中:x、y、h、z为系统转速、接力器位置、水压、转速变化变量;Tw、Ta、Ty分别为水流惯性时间常数、机组惯性常数、接力器常数;exm、eym、ehm、eqxm、eqhm、eqym为线性水轮机组常数;eg为电网自调节系数;r、mg0分别为转速和力矩扰动; kp、ki、kd为PID调节参数.
2.2 平衡点分析上述方程组中,系统的平衡点位置与初始扰动状态有关,分3种情况:
1) 当r=0、mg0=0时,系统有唯一的平衡点:(0,0,0,0),系统无扰动;
2) 当r=0、mg0≠0时,系统有唯一的平衡点:(0,mg0/eym,0,mg0/kieym),存在负荷扰动;
3) 当r≠0、mg0=0时,系统有唯一的平衡点:(r,(eg-exm)r/eym,0,(eg-exm)r/kieym),存在频率扰动.
2.3 Hopf分岔以某实际电站为例,某典型工况下,水轮机调节系统的参数分别为:Tw=2.0 s,Ta=6.87 s,exm=-1.067 3,eg=0.4,eym=0.771 3,ehm=1.717 9,eqxm=-0.290 1,eqhm=0.725 7,eqym=0.818 4,Ty=0.1 s,则以上各系数为
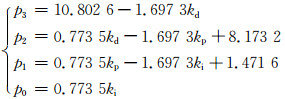 (13)
(13)
用定理3来判断系统Hopf分岔存在性时,要求特征多项式系数pi>0,由p3>0,可得kd < 6.364 6,即Hopf分岔区域在kd < 6.364 6内.将式(13)代入式(2),PID参数在出现Hopf分岔时应满足如下关系:
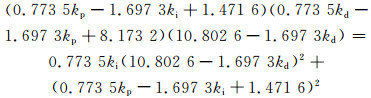 (14)
(14)
当以vd=kd-kd*或vp=kp-kp*作为分岔参数时,定理3中条件2左边为0,而右边不等于0,条件2成立.根据定理,系统将在|v|充分小时出现Hopf分岔现象,根据定理3和式(3),发生Hopf分岔时极限环周期与PID控制参数的关系为
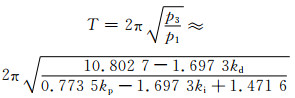 (15)
(15)
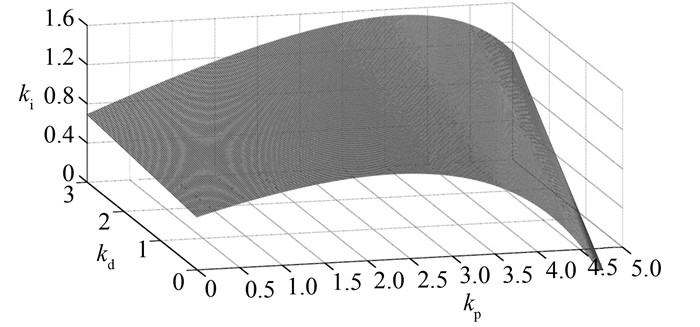
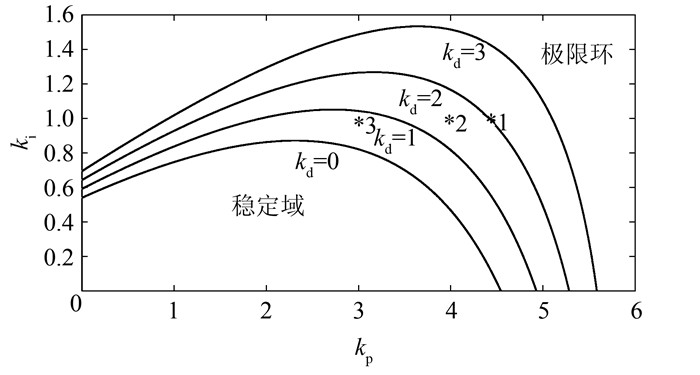
根据线性系统理论的Hurwitz稳定判据,可获得系统在PID参数空间中的稳定域,由式(14)给出系统在PID参数空间的分岔曲面,如图 2所示,该曲面将空间划分为稳定域和极限环两个性质不同的区域,曲面上每一点都可能是Hopf分岔临界点.Hopf分岔理论研究系统动力学特性的任务之一就是要确定这些分岔临界点,以确定系统稳定域边界及稳定域大小.为此,可在无扰动时由kd取不同值在PI参数平面作出稳定域和极限环,其中,kd分别取0、1、2和3,如图 3所示.
|
| 图 2 Hopf分岔空间曲面 Figure 2 Space surface of Hopf bifurcation |
|
| 图 3 PI参数平面上的稳定域和极限环区域 Figure 3 Stable region and limit cycle domain in PI parameter plane |
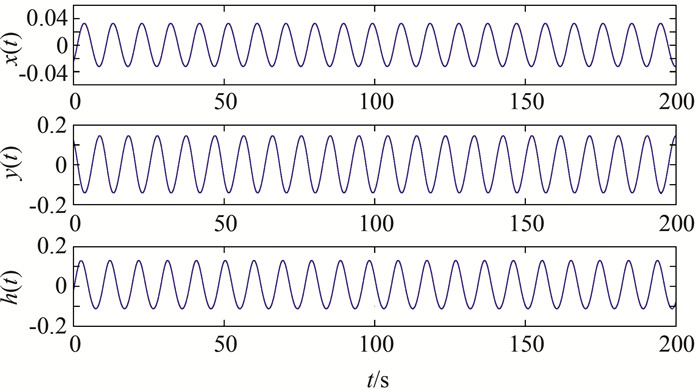
图 3中点1:kd=2,ki=1,由式(14)得kp=4.424 7,vp=0.图 4为机组转速x、接力器y和水头h在1点时的等幅低频振荡曲线, 由式(15)可计算出等幅振荡的周期为9.565 s, 与图 4中的仿真结果相一致.
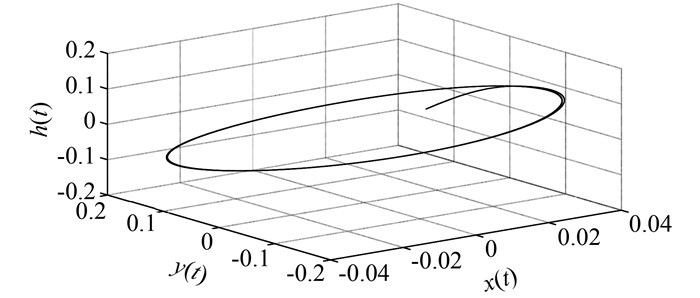
图 5、6为图 4对应的系统变量相空间轨道,可以观察到在相空间一定区域中所形成的闭轨道极限环,系统呈扩散的增幅非线性振荡曲线,表明系统出现临界Hopf分岔.
|
| 图 4 状态变量x、y、h的稳定振荡曲线 Figure 4 Stable oscillation curves of state variables x, y, h |
|
| 图 5 x、y、h相空间极限环 Figure 5 Limit cycle in x, y, h phase space |
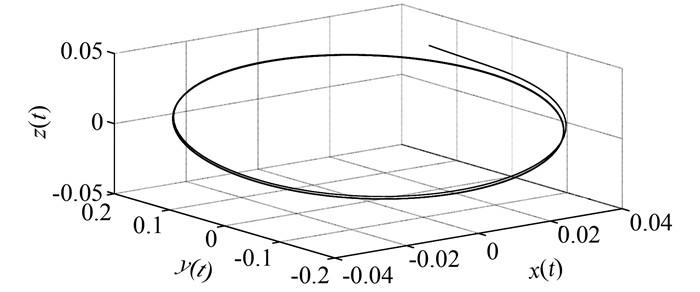
|
| 图 6 x、y、z相空间极限环 Figure 6 Limit cycle in x, y, z phase space |
上述图只给出了PID参数空间中Hopf分岔点的位置,但分岔方向及其稳定性的确定需要进一步计算.以vp=kp-kp*作分岔参数为例,在分岔点处系统Jacobi矩阵一对纯虚特征值为
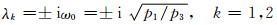
将式(13)代入式(2),可计算出系统纯虚特征值对vp导数的实部为
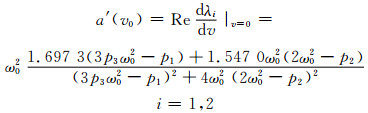
同理,可计算出系统纯虚特征值对vp导数虚部的表达式.在分岔点kp=4.424 7、ki=1.0、kd=2.0处,可计算出a′(v0)=0.138 5,再采用中心流形降阶方法[9]可直接计算β=-2.075 2 < 0.根据定理2可判断系统Hopf分岔是超临界的,极限环将出现在分岔参数v0>0一侧;而在v0 < 0一侧系统是渐近稳定的.下面通过PI参数平面图 3上给出2、3点的参数对系统稳定性进行验证.
图 3中2点:kd=2,ki=1,取vp=-0.4,则可得kp=4.024 7,图 7为机组转速x、接力器y和水头h在2点时受2.5 Hz初始频率扰动下的振荡曲线,由式(15)可计算出振荡的周期为10.345 s,可知,系统在该组参数下逐渐趋于稳定,且振荡周期与计算值一致,如图 7所示.
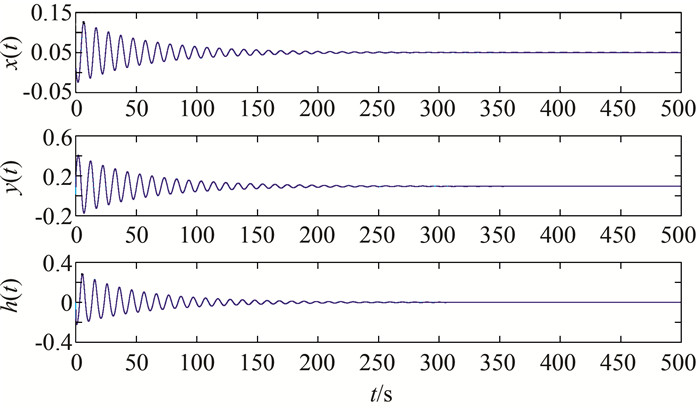
|
| 图 7 点2状态变量x、y、h的时域响应曲线 Figure 7 Time-domain response curves of state variables x, y, h |
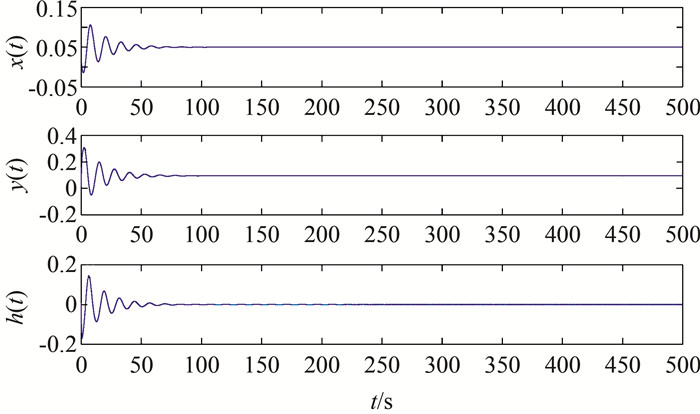
图 3中3点:kd =2,ki=1,取vp=-1,得到kp=3.424 7, 图 8为机组转速x、接力器y和水头h在3点时受2.5 Hz初始频率扰动时的振荡曲线,由式(15)可计算出振荡的周期为10.986 s,系统在该组参数下经过5个振荡周期后能迅速收敛于稳定点,该参数下系统是稳定的.
|
| 图 8 点3状态变量x、y、h的时域响应曲线 Figure 8 Time-domain response curves of state variables x, y, h |
图 4~8表明了系统的分岔方向及稳定性.当水轮机调节系统中采用PID(或增益调度PID)策略时,应将PID参数设置在图 3中极限环曲线下方且远离曲线的区域,否则系统中将有可能出现持续的或不稳定的增幅非线性振荡,而无法获得稳定的控制效果.
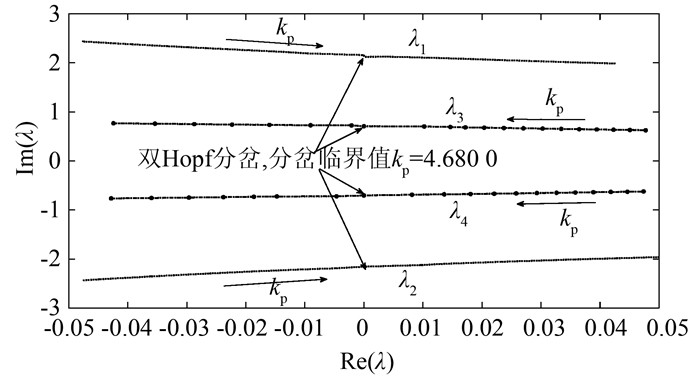
2.5 双Hopf分岔当kd=6.364 6,且kp与ki关系满足式(6)时,系统会出现双Hopf分岔现象.式(6)中,若取ki=3.0,则kp=4.680 3,PID参数空间中双Hopf分岔临界点之一为kp=4.680 0、ki=3.0、kd=6.364 6.计算得到此时系统Jacobi矩阵的两对特征值分别为-2.748 0-13±i0.706 1和-1.332 7-14±i2.157 3,考虑到数值计算中的允许误差,可认为两对共轭特征值的实部为0,系统存在两对纯虚特征根.图 9给出两对复共轭特征值随kp的变化在双Hopf分岔临界点处同时穿越虚轴的情况,两对复共轭特征值穿越方向相异,表明发生双Hopf分岔前后系统处于不稳定状态,与图 1(b)中的情况对应.
|
| 图 9 双Hopf分岔中特征值λ随kp的变化 Figure 9 Eigenvalues λ changes with kp of double Hopf bifurcation |
|
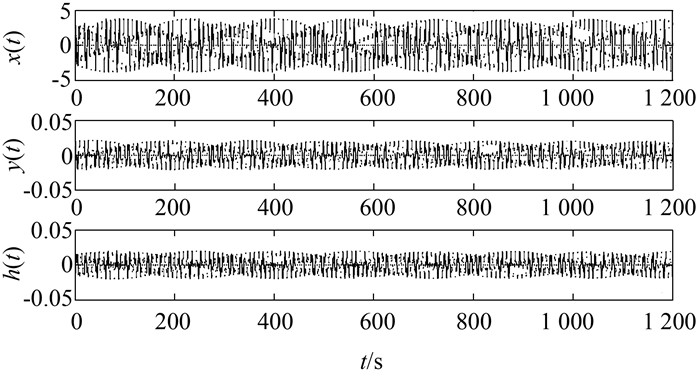
| 图 10 双Hopf分岔的振荡曲线 Figure 10 Oscillation curves of double Hopf bifurcation |
图 10为系统出现双Hopf分岔现象状态变量的时间振荡曲线,从中可观察到,从平衡点分岔出来的将不再是周期轨道,而可能是拟(准)周期轨道,两个不同频率的振荡相互叠加形成更为复杂的非线性振荡波形,该波形与非线性系统的Neimark-Sacker分岔(环面分岔)中的调制波形非常相似.
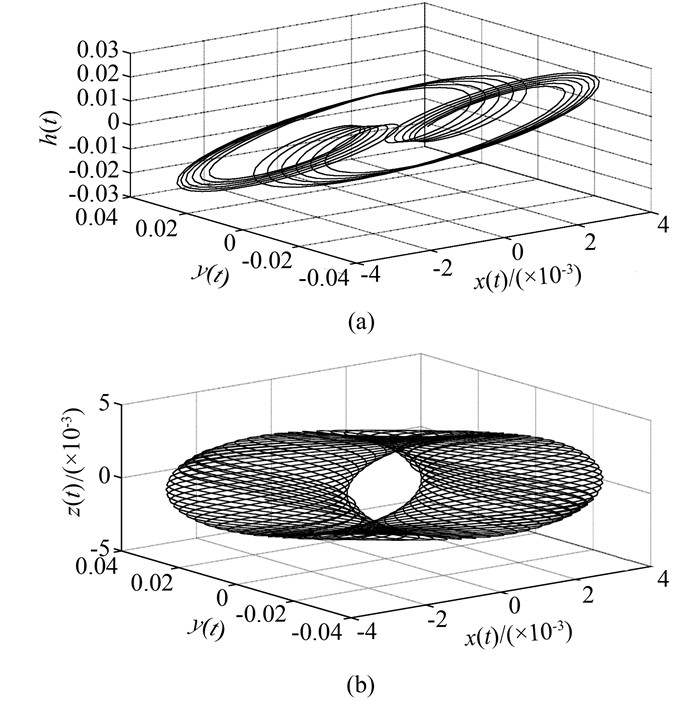
当发生双Hopf分岔时,在系统状态空间中将会出现闭轨道双极限环以及轮胎面或指环形的吸引域,如图 11所示,包含丰富的动力学特征,是一种比相空间中极限环更为复杂的非线性动态行为.
|
| 图 11 双Hopf分岔时x、y、z相空间极限环 Figure 11 Limit cycle in x, y, z phase space in double Hopf bifurcation |
当取弹性水击模型时,上述四维可扩展到六维[14, 15],水力系统参数Tr=1.35,hw=2,方程组为
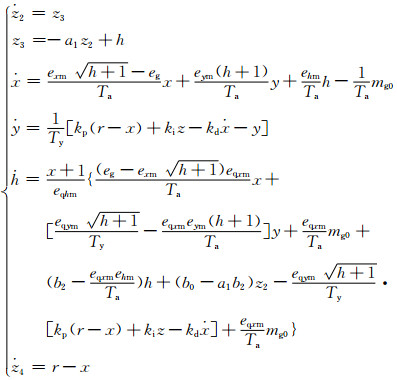
水轮机参数取值同上,且平衡点分析、Hopf分岔、分岔方向及稳定性可依据文中给出的公式和定理进行计算,分析过程及结果与四维系统的类似.根据六维非线性系统出现双Hopf分岔的必要条件式(12),给定ki时计算发生双Hopf分岔的a、b、kp、kd、ω1和ω2等值.表 1~3分别给出了无扰动、2.5 Hz频率扰动和30%负荷扰动时双Hopf分岔临界点及系统特征值的计算结果,在一定的PID参数范围内,系统Jacobi矩阵出现两对纯虚共轭特征值,且两对纯虚部值是系统发生双Hopf分岔时的两个振荡频率ω1和ω2,当系统以两个不同频率进行振荡时,将呈现出更为复杂的动态特性.
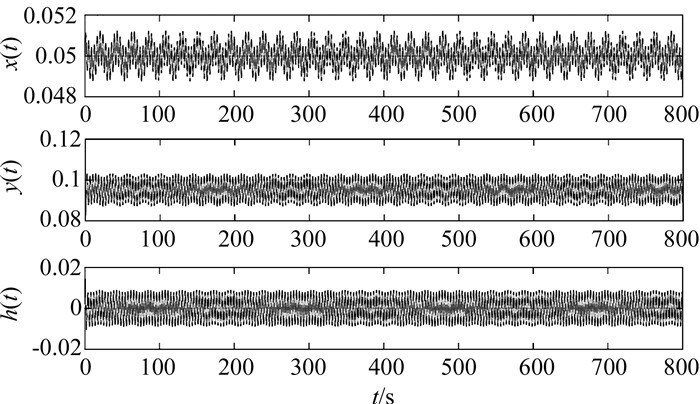
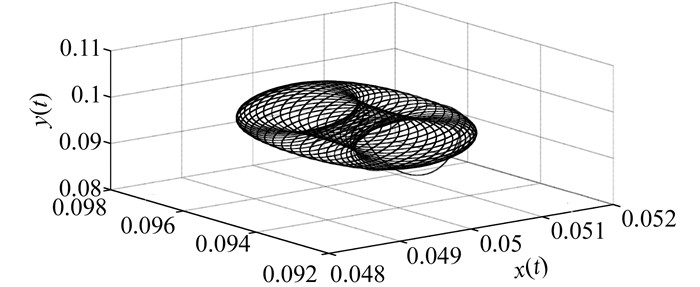
图 12、13为六维系统在PID控制参数分别为kp=1.315、ki=1、kd=5.591并受到2.5 Hz频率扰动的初始条件下,双Hopf分岔两个不同频率的状态变量振荡曲线相互迭加的时域响应图和对应的相空间吸引域.在流体力学关于湍流发生机制的理论中,这种拟(准)周期轨道所引发的轮胎面吸引域事实上也是发生湍流Landau-Hopf[16]理论分析的出发点.
| 分岔参数 | Jacbi矩阵特征值 | 振荡频率 | |||||
| kp | ki | kd | ω1 | ω2 | |||
| 0.043 | 0.6 | 6.177 | -0.58±i6.052 | ±i1.867 | ±i0.195 | 1.867 | 0.195 |
| 1.087 | 1.0 | 6.280 | -0.49±i5.970 | ±i1.716 | ±i0.267 | 1.716 | 0.267 |
| 2.573 | 1.5 | 6.413 | -0.38±i5.850 | ±i1.440 | ±i0.399 | 1.440 | 0.399 |
| 4.056 | 2.0 | 6.531 | -0.28±i5.730 | ±i0.896 | ±i0.756 | 0.896 | 0.756 |
| 3.945 | 2.5 | 7.068 | 0.18±i0.731 | ±i5.818 | ±i0.993 | 5.818 | 0.993 |
| 2.487 | 3.0 | 7.125 | 0.22±i0.499 | ±i5.962 | ±i1.460 | 5.962 | 1.460 |
| 1.352 | 3.5 | 7.167 | 0.26±i0.434 | ±i6.076 | ±i1.673 | 6.076 | 1.673 |
| 分岔参数 | Jacbi矩阵特征值 | 振荡频率 | |||||
| kp | ki | kd | ω1 | ω2 | |||
| 0.084 | 0.6 | 6.347 | 0.233±i1.851 | ±i6.197 | ±i0.196 | 6.197 | 0.196 |
| 1.133 | 1.0 | 6.336 | 0.221±i1.682 | ±i6.079 | ±i0.273 | 6.079 | 0.273 |
| 2.566 | 1.5 | 6.316 | 0.203±i1.373 | ±i5.918 | ±i0.420 | 5.918 | 0.420 |
| 3.617 | 2.0 | 6.303 | 0.190±i0.921 | ±i5.802 | ±i0.730 | 5.802 | 0.730 |
| 2.788 | 2.5 | 6.340 | 0.225±i0.540 | ±i5.893 | ±i1.291 | 5.893 | 1.291 |
| 1.623 | 3.0 | 6.379 | 0.264±i0.439 | ±i6.023 | ±i1.582 | 6.023 | 1.582 |
| 0.712 | 3.5 | 6.410 | 0.294±i0.393 | ±i6.127 | ±i1.753 | 6.127 | 1.753 |
| 分岔参数 | Jacbi矩阵特征值 | 振荡频率 | |||||
| kp | ki | kd | ω1 | ω2 | |||
| 0.299 | 0.6 | 5.535 | 0.247+i1.778 | ±i5.947 | ±i0.199 | 5.947 | 0.199 |
| 1.703 | 1.0 | 5.523 | 0.233±i1.451 | ±i5.768 | ±i0.324 | 5.768 | 0.324 |
| 2.982 | 1.5 | 5.513 | 0.222±i0.858 | ±i5.610 | ±i0.677 | 5.610 | 0.677 |
| 2.259 | 2.0 | 5.543 | 0.255±i0.478 | ±i5.700 | ±i1.259 | 5.700 | 1.259 |
| 1.264 | 2.5 | 5.575 | 0.291±i0.378 | ±i5.823 | ±i1.564 | 5.823 | 1.564 |
| 0.447 | 3.0 | 5.601 | 0.319±i0.329 | ±i5.928 | ±i1.752 | 5.928 | 1.752 |
|
| 图 12 六维系统双Hopf分岔的振荡曲线 Figure 12 Oscillation curves of double Hopf bifurcation of six dimensional system |
|
| 图 13 六维系统双Hopf分岔时x、z、y相空间极限环 Figure 13 Limit cycle in x, z, y phase space in double Hopf bifurcation of six dimensional system |
本文基于非线性动力系统的分岔理论,分别对水轮机调节系统的刚性和弹性水击连续时间非线性解析模型进行了理论分析,给出了系统在PID参数空间中不同情况下的稳定域范围,证明了所研究的非线性系统均存在超临界Hopf分岔现象,由于其经分岔产生的极限环是稳定的,因而可进一步观察系统的分岔特性,包括分岔参数的临界值、在稳定域内的平衡点位置以及发生分岔时极限环的方向等;给出了判断系统出现双Hopf分岔的必要条件,对水轮机调节系统的四维和六维非线性模型进行了双Hopf分岔的存在性的计算,对于考虑水轮机的传递系数随工况变化的非线性动态模型,无论是刚性水击还是弹性水击模型,都存在双Hopf分岔现象,通过计算给出了发生双Hopf分岔时的参数值.最后, 通过数值计算对分岔点两侧系统稳定性的变化情况进行仿真,验证了理论分析结果.文中的分析方法适用于一般水力发电系统的稳定运行分析和研究, 从而为水轮机调节系统中控制参数的正确选择提供了一条新的理论分析途径.
| [1] |
李云.
非线性动力系统的现代数学方法及其应用[M]. 北京: 人民交通出版社, 1998.
Li Yun. Modern Mathematical Methods and Their Application of Nonlinear Dynamic System[M]. Beijing: People's Commumication Press, 1998. |
| [2] | Hassard B D, Kazarinoff N D, Wan Y H. Theory and Applications of Hopf Bifurcation[M]. Beijing: Cambridge University Press, 1981. |
| [3] | Che Y Q, Wang J, Zhou S S. Robust synchronization control of coupled chaotic neurons under external electrical simulation[J]. Chaos, Solitons & Fractals, 2009, 40(3): 1333–1342. |
| [4] | Wu W J. Complex nonlinear dynamics and controlling chaos in a cournot duopoly economic model[J]. Nonlinear Analysis:Real World Applications, 2010, 11(5): 4363–4377. DOI:10.1016/j.nonrwa.2010.05.022 |
| [5] |
高学军, 李映辉, 乐源. 延续算法在简单轨道客车系统分岔中的应用[J].
振动与冲击, 2012, 20(31): 177–182.
Gao Xuejun, Li Yinghui, Yue Yuan. Continuation method and its application in bifurcation of a railway passenger car system with simple rails[J]. Journal of Vibration and Shock, 2012, 20(31): 177–182. |
| [6] |
刘伟渭, 戴焕云, 曾京. 轨道随机激励对弹性约束轮对随机稳定性与随机分岔的影响[J].
振动与冲击, 2013, 21(32): 170–178.
Liu Weiwei, Dai Huanyun, Zeng Jing. Influence of rail stochastic excitation on stochastic stability and stochastic bifurcation of an elastic constraint wheel set system[J]. Journal of Vibration and Shock, 2013, 21(32): 170–178. |
| [7] |
陈帝伊, 杨朋超, 马孝义, 等. 水轮机调节系统的混沌现象分析及控制[J].
中国电机工程学报, 2011, 15(31): 113–120.
Chen Diyi, Yang Pengchao, Ma Xiaoyi, et al. Chaos of hydro-turbine governing system and its control[J]. Proceedings of the CSEE, 2011, 15(31): 113–120. |
| [8] |
凌代俭, 陶阳, 沈祖诒. 考虑弹性水击效应时水轮机调节系统的Hopf分岔分析[J].
振动工程学报, 2007, 20(4): 374–379.
Ling Daijian, Tao Yang, Shen Zuyi. Hopf bifurcation analysis of hydraulic turbine governing systems with elastic water hammer effect[J]. Journal of Vibration Engineering, 2007, 20(4): 374–379. |
| [9] |
凌代俭, 沈祖诒. 水轮机调节系统的非线性模型、PID控制及其Hopf分岔[J].
中国电机工程学报, 2005, 25(10): 97–102.
Ling Daijian, Shen Zuyi. The nonlinear model of hydraulic turbine governing systems and its PID control and hopf bifurcation[J]. Proceedings of the CSEE, 2005, 25(10): 97–102. DOI:10.3321/j.issn:0258-8013.2005.10.018 |
| [10] | Yu P. Symbolic computation of normal forms for resonant double Hopf bifurcations using multiple time scales[J]. Journal of Sound and Vibration, 2001, 247(4): 615–632. DOI:10.1006/jsvi.2001.3732 |
| [11] | Luongo A, Di Egidio A. Multiscale analysis of defective multiple Hopf bifurcations[J]. Computers and Structures, 2004, 82: 2705–2722. DOI:10.1016/j.compstruc.2004.04.022 |
| [12] | Bi Q, Yu P. Double Hopf bifurcations and chaos of a nonlinear vibration system[J]. Nonlinear Dynamics, 1999, 19: 313–332. DOI:10.1023/A:1008347523779 |
| [13] | Bi Q. Symbolic software development for computing the normal form of double Hopf bifurcation[J]. Mathematical and Computer Modeling Volume, 1999, 29(9): 49–70. DOI:10.1016/S0895-7177(99)00081-3 |
| [14] |
凌代俭. 水轮机调节系统分岔与混沌特性的研究[D]. 南京: 河海大学, 2007.
Ling Daijian. Study of bifurcation and chaos characteristics in hydro-turbine regulating system[D]. Nanjing: Hohai University, 2007. |
| [15] |
沈祖诒.
水轮机调节系统[M]. 第3版. 北京: 水利电力出版社, 1998.
Shen Zuyi. Hydroturbine Governing System[M]. Third Edition. Beijing: Hydraulicand Power Press, 1998. |
| [16] |
盛昭瀚, 马军海.
非线性动力系统分析引论[M]. 北京: 科学出版社, 2001.
Sheng Zhaohan, Ma Junhai. Introduction to Analysis of Nonlinear Dynamic System[M]. Beijing: Science Press, 2001. |
 2018, Vol. 51
2018, Vol. 51




