武汉大学学报(工学版)   2016, Vol. 49 Issue (3): 347-351

文章信息

肖阳, 谈广鸣, 翁朝晖, 舒彩文, 陈一明
XIAO yang, TAN Guangming, WENG Zhaohui, SHU Caiwen, CHEN Yiming
基于灰色层次分析法的城市防洪工程效益评价
Research and application of benefits assessment for urban flood control project based on gray AHP
武汉大学学报(工学版), 2016, 49(3): 347-351
Engineering Journal of Wuhan University, 2016, 49(3): 347-351
http://dx.doi.org/10.14188/j.1671-8844.2016-03-005

文章历史

收稿日期: 2015-12-23
 Abstract              PDF               Figures               Tables
引用本文 0
肖阳, 谈广鸣, 翁朝晖, 舒彩文, 陈一明. 基于灰色层次分析法的城市防洪工程效益评价[J]. 武汉大学学报(工学版), 2016, 49(3): 347-351.
XIAO yang, TAN Guangming, WENG Zhaohui, SHU Caiwen, CHEN Yiming. Research and application of benefits assessment for urban flood control project based on gray AHP[J]. Engineering Journal of Wuhan University, 2016, 49(3): 347-351.
基于灰色层次分析法的城市防洪工程效益评价
肖阳1,2, 谈广鸣1, 翁朝晖2, 舒彩文1, 陈一明1     
1. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;
 2. 湖北省水利水电规划勘测设计院，湖北 武汉 430064
收稿日期: 2015-12-23
作者简介: 肖阳（1990-），女，硕士研究生，主要从事城市防洪工程效益评价研究，E-mail: youngwhu@126.com.
通讯作者: 谈广鸣（1958-），男，教授，博士生导师，主要从事水力学及河流动力学、国际河流管理研究，E-mail: tangm@vip.163.com
基金项目: 国家自然科学基金重点项目（编号： 51339004）；国家自然科学基金项目（编号：51309180）.
摘要: 层次分析法是定性与定量分析相结合的多准则决策方法，而灰色区间关联法能进行既有确知信息又含有未知信息的关联分析.根据城市防洪工程效益评价范围宽、层次多、评价指标多样化的特点，运用层次分析法建立效益评价模型，确定城市防洪工程效益的影响指标及其权重值，并结合灰色区间关联法进行关联运算，进而提供最优方案的选择方法.针对长江中下游的沿江城市武汉市的城市防洪工程，运用上述灰色层次分析法评价模型分析该城市“有”、“无”防洪工程相对于理想方案的关联度，进而对其防洪工程效益进行分析评价.模型计算结果表明，该城市的防洪工程发挥了较显著的综合效益.
关键词： 城市防洪     效益评价     灰色层次分析法    
Research and application of benefits assessment for urban flood control project based on gray AHP
XIAO yang1,2, TAN Guangming1, WENG Zhaohui2, SHU Caiwen1, CHEN Yiming1     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. Hubei Provincial Water Resources and Hydropower Planning, Survey and Design Institute, Wuhan 430064, China
Abstract: Analytic hierarchy process (AHP) is a qualitative and quantitative approach in multiple criteria decision making; while grey interval correlation method can conduct correlation analysis with both ascertain and uncertain information. The benefit assessment of urban flood control project is characterized with wide range, multilevel and diversified index. For this characteristic, an AHP assessment model combined with grey interval correlation method is proposed to evaluate the optimal program of urban flood control. The impact indicators and its weights are determined by the AHP assessment model; the correlation degrees for different schemes are calculated using grey interval correlation method. Finally, the developed method is applied to assessing the benefits of the urban flood control project in Wuhan city along Yangtze River. The correlation degree for schemes of building or not building the flood control project related to the ideal one is calculated. The results demonstrate that the flood control project in this city has significant comprehensive benefits.
Key words: urban flood control     benefits assessment     gray analytic hierarchy process    

随着我国城镇化建设步伐的加快，城市成为经济、政治、文化高度集中的区域，相应地对城市防洪综合效益提出了更严格的要求.城市防洪工程通过减免一定频率的洪水灾害损失发挥其社会经济效益，同时，城市河道经过整治美化，使城市景观得到极大的改善.这不仅满足了居民亲水临水的愿景，丰富了居民业余生活，还带动防洪工程周边土地升值、商业开发等间接效益.近几年，各个城市在防洪建设和防汛方面开展大规模的河道整治、恢复兴建大量的防洪工程、对老化的防洪设施进行全面的除险加固，在一定程度上提高了城市防洪能力[1~4].

城市防洪工程效益评价范围宽、层次多，评价指标多样化.本文主要基于城市河道堤防工程、城市排涝工程以及江滩景观工程的综合功能，首先采用定性与定量分析相结合的层次分析法(Analytic Hierarchy Process，AHP)，并结合相关规范[5~7]，建立城市防洪工程效益评价模型，确定评价指标的权重值.在此基础上，结合灰色区间关联法，分析长江中下游沿江城市武汉市“有”、“无”防洪工程相对于理想方案的关联度，评价该城市防洪工程的综合效益.

1 层次分析法

层次分析法将研究的问题分解为不同的组成因素，按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，最终把系统分析归结为评价指标相对于最高层(总目标)的相对重要性权值的确定或相对优劣次序的排序问题[8~10].

1.1 评价模型建立

“城市防洪工程效益评价”为评价模型的目标层；城市防洪工程效益评价的准则层分别为“经济效益”、“社会效益”、“环境效益”以及“景观效益”；最底层表示准则层中15个评价指标.评价模型如图 1所示.

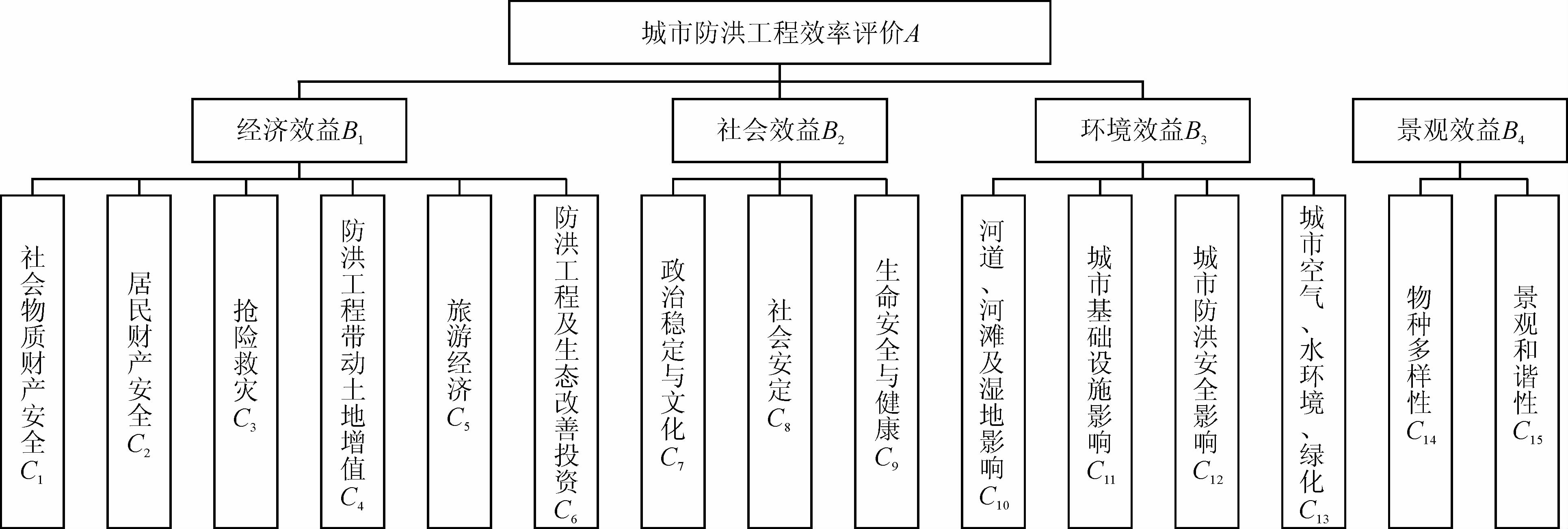
图 1 城市防洪工程效益评价层次分析法模型 Figure 1 AHP model of urban flood control project benefit evaluation
图选项
1.2 构造判断矩阵

判断矩阵表示针对上一层次因素，本层次与之有关因素之间相对重要性的比较[8].对模型中成对因素进行两两比较，并通过A.L.Saaty引用的1~9标度法,用数值表示出来，构造判断矩阵.1~9标度中1、3、5、7、9分别表示两个因素相比，一个因素比另一个因素同样、稍微、明显、强烈、极端重要；2、4、6、8分别表示上述两相邻判断数值的中值.本文根据层次分析法效益评价模型构造的各层次判断矩阵分别列于表 1~5.

表 1 A-B判断矩阵 Table 1 Judgment matrix A-B
A B1 B2 B3 B4
B1 1 1/3 3 5
B2 3 1 5 7
B3 1/3 1/5 1 3
B4 1/5 1/7 1/3 1
特征向量W=[0.263 3，0.557 9，0.121 9，0.056 9]
λmax=4.118 5，CI=0.039 5，CR=0.04<0.10
表选项
表 2 B1-C判断矩阵 Table 2 Judgment matrix B1-C
B1 C1 C2 C3 C4 C5 C6
C1 1 4 1/3 5 5 4
C2 1/4 1 1/5 3 4 1/3
C3 3 5 1 6 7 5
C4 1/5 1/3 1/6 1 2 1/4
C5 1/5 1/4 1/7 1/2 1 1/5
C6 1/4 3 1/5 4 5 1
特征向量W=[0.249 6，0.095 7，0.422 1，0.050 8，0.035 8，0.146 0]
λmax=4.118 5, CI=0.108 1，CR=0.09<0.10
表选项
表 3 B2-C判断矩阵 Table 3 Judgment matrix B2-C
B2 C7 C8 C9
C7 1 3 1/3
C8 1/3 1 1/5
C9 3 5 1
特征向量W=[0.260 5，0.106 1,0.633 4]
λmax=3.038 2, CI=0.019 0,CR=0.03<0.10
表选项
表 4 B3-C判断矩阵 Table 4 Judgment matrix B3-C
B3 C10 C11 C12 C13
C10 1 4 3 4
C11 1/4 1 1/3 1
C12 1/3 3 1 3
C13 1/4 1 1/3 1
特征向量W=[0.502 7,0.102 8,0.316 4,0.078 1]
λmax=4.214 0, CI=0.071 3,CR=0.08<0.10
表选项
表 5 B4-C判断矩阵 Table 5 Judgment matrix B4-C
B4 C14 C15
C14 1 1/2
C15 2 1
特征向量W=[0.333 3,0.666 7]
λmax=2.000 0, CI=0,CR=0<0.10
表选项
1.3 层次排序与一致性检验

判断矩阵使决策者的判断思维数学化和定量化，引入判断矩阵最大特征值以外的其余特征值的负平均值作为度量判断矩阵偏离一致性的指标.即$CI=\frac{{{\lambda }_{\max }}-n}{n-1}$，其中：λmax为判断矩阵的最大特征根，n为判断矩阵阶数，本文采用和积法计算最大特征根，并列于表 1~5中.根据判断矩阵的平均随机一致性指标RI计算出随机一致性比率$CR=\frac{CI}{RI}＜0.10$时，表明层次单排序的结果有合理的一致性，否则需调整判断矩阵的元素取值.其中RI根据判断矩阵的阶数取值如表 6所示.

表 6 判断矩阵RI取值 Table 6 Judgment matrix value of RI
阶数1 2 3 4 5 6 7 8 9
RI0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45
表选项

B层次总排序随机一致性比率为

$\text{RI}=\sum\limits_{j=1}^{m}{\left( {{a}_{j}}C{{I}_{j}} \right)}/\sum\limits_{j=1}^{m}{\left( {{a}_{j}}\text{R}{{\text{I}}_{j}} \right)}$    (1)

其中：CIj为B层次某因素对于Aj单排序的一致性指标；CRj为相应的平均随机一致性指标.

1.4 效益评价指标权重值确定

层次单排序、一致性检验以及层次总排序结果列于表 7.由表 7可知，准则层中社会效益B2权重值最大(0.557 9)，其次为经济效益B1(0.263 3)和环境效益B3(0.121 9).将各个评价指标权重值(百分比)绘于图 2，由图 2可知，生命安全与健康C6所占权重最大(0.353 4)，这符合我国建设城市防洪工程的初衷.

表 7 层次指标排序 Table 7 Sequence of hierarchy index
评价指标 B1 B2 B3 B4 总排序
0.263 3 0.557 9 0.121 9 0.056 9
C1 0.249 6 0.065 7
C2 0.095 7 0.025 2
C3 0.422 1 0.111 2
C4 0.050 8 0.013 4
C5 0.035 8 0.009 4
C6 0.146 0 0.038 4
C7 0.260 5 0.145 3
C8 0.106 1 0.059 2
C9 0.633 4 0.353 4
C10 0.502 7 0.061 3
C11 0.102 8 0.012 5
C12 0.316 4 0.038 6
C13 0.078 1 0.009 5
C14 0.333 3 0.019 0
C15 0.666 7 0.037 9
表选项
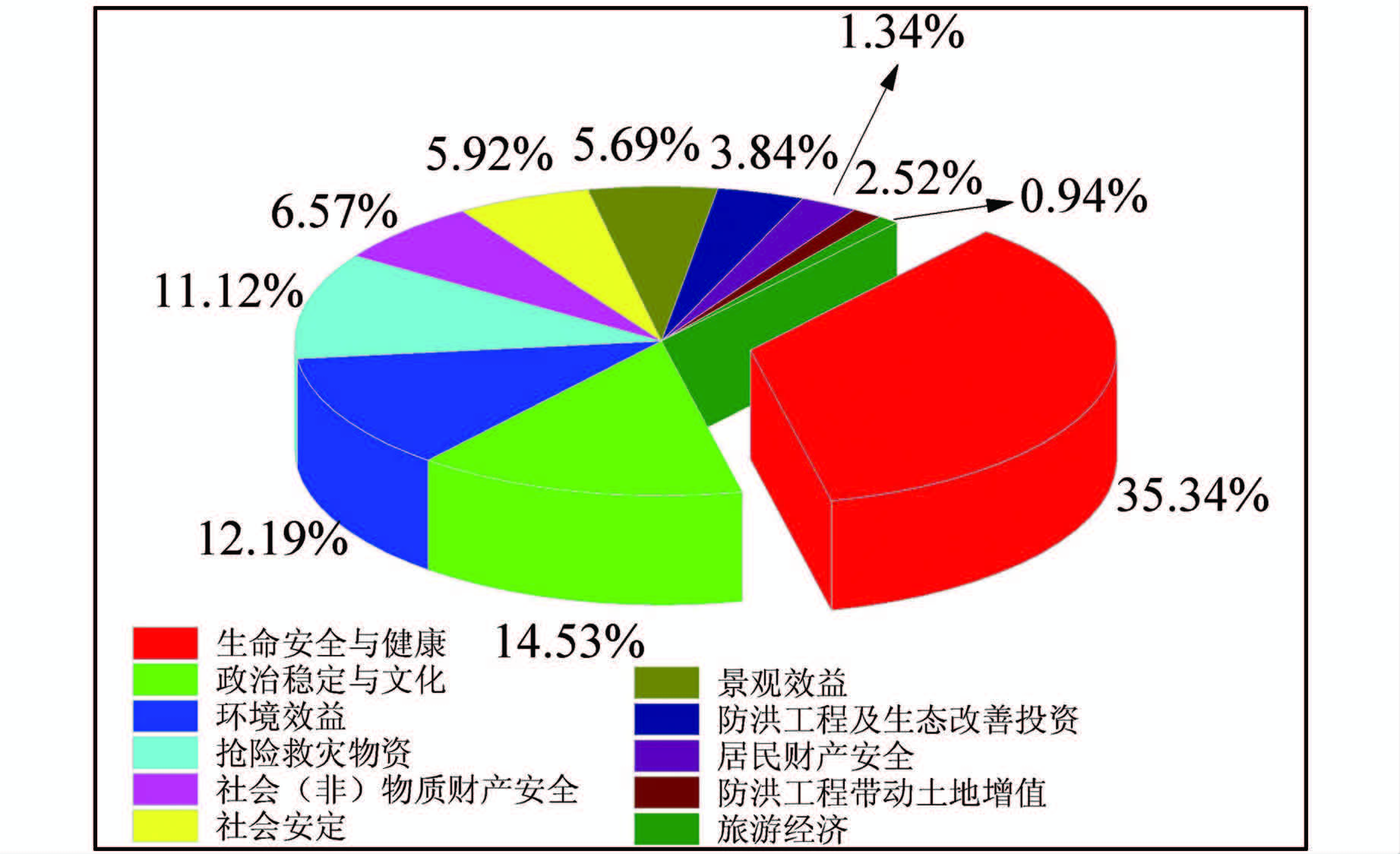
图 2 城市防洪工程效益各指标比例 Figure 2 Proportion of every index in urban flood control project benefits
图选项

层次总排序一致性检验：

$CI=\sum\limits_{i=1}^{n}{{{C}_{i}}CI}$    (2)
$RI=\sum\limits_{i=1}^{n}{{{C}_{i}}RI}$    (3)

计算本文的$CR=\frac{CI}{RI}\text{=}0.06＜0.10$，表明判断矩阵和各权重值合理.

2 灰色区间关联法

灰色决策理论是20世纪80年代后期开始逐步发展起来的一类解决不确定性决策问题的分析方法.灰色区间关联法是灰色决策理论的核心方法之一，依据问题的实际背景，找出理想最优方案对应的效果评价向量，由决策问题中各个方案的效果评价向量与理想最优方案的效果评价向量之间灰色关联度的大小来确定问题的最优方案及方案的优劣排序[11].

3 实例评价

对已建的城市防洪工程进行效益评价，在层次分析法的基础上引入灰色区间关联法，通过计算“有”与“无”防洪工程相对于防洪工程效益理想方案的关联度，关联度最大的方案即为效益最优方案[11, 12].

设武汉市建设城市防洪工程为决策A1，不建设防洪工程为决策A2，理想方案表示为A.通过查阅武汉市防洪工程相关报告与文献，将15个指标取为区间灰数.其中：抢险救灾C3采用1954年该城市特大洪水救灾物资价值(单位：元)，防洪工程带动土地增值C4根据量化模型[13~15]计算而得(单位：元/m2)，旅游经济C5采用汉口旅游报告中相关数据(单位：亿元)，防洪工程及生态改善投资C6采用相关报告数据(单位：亿元)，城市空气、水环境、绿化C13根据相关报告用百分比表示改善程度；其余指标均根据评分用十分制或百分数表示.其中C3、C6为成本型指标，其余指标为效益型指标.省略各指标量纲，具体数据列于表 8.

表 8 评价指标区间灰数及标准数 Table 8 The interval gray and criteria numbers
评价指标 区间灰数 标准值 最优值A
A1 A2 A1 A2
C1 [7, 8] [6, 7] [0.5,1] [0,0.5] [0.5,1]
C2 [7, 7] [6, 7] [0.5,1] [0,0.5] [0.5,1]
C3 [0, 0] [80, 130] [1, 1] [0.385,0] [1, 1]
C4 [100, 130] [50, 60] [0.625,1] [0,0.125] [0.625,1]
C5 [5,6.37] [5,6.36] [0, 1] [0,0.992] [0, 1]
C6 [11, 16] [0, 0] [0.313,0] [1, 1] [1, 1]
C7 [6, 9] [7, 8] [0, 1] [0.333,0.667] [0, 1]
C8 [7, 9] [7, 8] [0, 1] [0,0.5] [0, 1]
C9 [8, 9] [7, 7] [0.5,1] [0, 0] [0.5,1]
C10 [6, 7] [5, 7] [0.5,1] [0, 1] [0.5,1]
C11 [6, 9] [7, 8] [0, 1] [0.333,0.667] [0, 1]
C12 [7, 8] [6, 7] [0.5,1] [0,0.5] [0.5,1]
C13 [70%,80%] [50%,60%] [0.667,1] [0,0.333] [0.667,1]
C14 [60%,80%] [40%,50%] [0.5,1] [0,0.25] [0.5,1]
C15 [60%,90%] [30%,50%] [0.5,1] [0,0.333] [0.5,1]
表选项

1) 将各个方案效益值进行标准化处理.

成本型目标值标准化：

${{\underline{x}}_{ij}}=\frac{\overline{u}_{j}^{*}-{{\overline{u}}_{ij}}}{\overline{u}_{j}^{*}-\underline{u}_{j}^{\nabla }},{{\overline{x}}_{ij}}=\frac{\overline{u}_{j}^{*}-{{\overline{u}}_{ij}}}{\overline{u}_{j}^{*}-\underline{u}_{j}^{\nabla }}$    (4)

效益型目标值标准化：

${{\underline{x}}_{ij}}=\frac{{{\underline{u}}_{ij}}-\underline{u}_{j}^{\nabla }}{\overline{u}_{j}^{*}-\underline{u}_{j}^{\nabla }},{{\overline{x}}_{ij}}=\frac{{{\overline{u}}_{ij}}-\underline{u}_{j}^{\nabla }}{\overline{u}_{j}^{*}-\underline{u}_{j}^{\nabla }}$    (5)

其中：$\bar u_j^* = \mathop {\max }\limits_{1 \leqslant i \leqslant n} {\mkern 1mu} \left\{ {{{\bar u}_{ij}}} \right\},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {u} _j^\nabla {\text{ = }}\mathop {\min }\limits_{1 \leqslant i \leqslant n} {\mkern 1mu} \left\{ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {u} }_{ij}}} \right\},j = 1,2,...,m$.本文标准化区间灰数见表 8.

2) 构造理想方案效果评价向量.

$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {x} _j^ + = \mathop {\max }\limits_{1 \leqslant i \leqslant n} {\mkern 1mu} \left\{ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {x} }_{ij}}} \right\},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {x} _j^ - = \mathop {\min }\limits_{1 \leqslant i \leqslant n} {\mkern 1mu} \left\{ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {x} }_{ij}}} \right\},\bar x_j^ + = \mathop {\max }\limits_{1 \leqslant i \leqslant n} {\mkern 1mu} \left\{ {{{\bar x}_{ij}}} \right\},\bar x_j^ - = \mathop {\min }\limits_{1 \leqslant i \leqslant n} {\mkern 1mu} \left\{ {{{\bar x}_{ij}}} \right\}(j = 1,2,...,m)$    (6)
${x^ + }( \otimes ) = \left( {x_1^ - \left( \otimes \right),x_2^ - \left( \otimes \right),...,x_m^ - \left( \otimes \right)} \right)$    (7)

其中：$x_j^ + \left( \otimes \right) \in \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}\to {x} _j^ + ,\bar x_j^ + } \right]$(j=1,2,…,m).本文理想方案效果评价向量取值列于表 8第6列.

3) 计算灰色区间关联系数.

$r_{ij}^{+}=\frac{1}{2}\left[ \frac{\underset{1\le i\le n}{\mathop{\min }}\,\underset{1\le j\le m}{\mathop{\min }}\,\left| \underline{x}_{j}^{+}-{{\underline{x}}_{ij}} \right|+\lambda \underset{1\le i\le n}{\mathop{\max }}\,\underset{1\le j\le m}{\mathop{\max }}\,\left| \underline{x}_{j}^{+}-{{\underline{x}}_{ij}} \right|}{\left| \underline{x}_{j}^{+}-{{\underline{x}}_{ij}} \right|+\lambda \underset{1\le i\le n}{\mathop{\max }}\,\underset{1\le j\le m}{\mathop{\max }}\,\left| \underline{x}_{j}^{+}-{{\underline{x}}_{ij}} \right|}+\frac{\underset{1\le i\le n}{\mathop{\min }}\,\underset{1\le j\le m}{\mathop{\min }}\,\left| \overline{x}_{j}^{+}-{{\overline{x}}_{ij}} \right|+\lambda \underset{1\le i\le n}{\mathop{\max }}\,\underset{1\le j\le m}{\mathop{\max }}\,\left| \overline{x}_{j}^{+}-{{\overline{x}}_{ij}} \right|}{\left| \overline{x}_{j}^{+}-{{\overline{x}}_{ij}} \right|+\lambda \underset{1\le i\le n}{\mathop{\max }}\,\underset{1\le j\le m}{\mathop{\max }}\,\left| \overline{x}_{j}^{+}-{{\overline{x}}_{ij}} \right|} \right]$    (8)

式中：rij+为灰色区间关联系数;λ∈0,1,为分辨系数，本文取0.5;i=1,2,…,n;j=1,2,…,m.

理想方案的多目标灰色关联系数向量式：

$r_{i}^{+}=\left( r_{i1}^{+},r_{i2}^{+},...,r_{im}^{+} \right)$    (9)

式中：i=1,2,…,n，表示n个决策方案.计算结果见表 9.

表 9 关联系数与关联度 Table 9 Correlation coefficient rij and correlation degree G
评价 指标 关联系数rij 权重值w 关联度
A1 A2 A1 A2
C1 1 0.450 0.066 0.93 0.50
C2 1 0.450 0.025
C3 1 0.342 0.111
C4 1 0.440 0.013
C5 1 0.668 0.009
C6 0.330 1 0.038
C7 0.750 0.800 0.145
C8 1 0.750 0.059
C9 1 0.306 0.353
C10 1 0.700 0.061
C11 0.750 0.800 0.013
C12 1 0.450 0.039
C13 1 0.381 0.010
C14 1 0.400 0.019
C15 1 0.414 0.038
表选项

4)计算各方案与理想方案的灰色区间关联度.

$G=\sum\limits_{j=1}^{m}{{{w}_{j}}r_{ij}^{+}}$    (10)

其中：wj为目标权重向量中第j个元素值，取层次分析法计算的权重值.计算结果列于表 9.

经计算，武汉市如果不建设防洪工程，相对于理想方案的灰色区间关联度G2=0.50，建设防洪工程，相对理想方案的灰色区间关联度G1=0.93>0.50，根据灰色区间关联法，关联度最大对应的方案为最优方案,表明该城市建设防洪工程为最优方案，即武汉市已建的防洪工程带来了较显著的综合效益.

4 结论

1) 采用层次分析法计算城市防洪工程效益各准则层的权重值，准则层中社会效益(0.56)权重值最大；本文所列举的15个城市防洪工程效益指标中，人民的生命安全指标(0.35)所占权重最大，符合建设城市防洪工程的初衷.

2) 灰色区间关联度评价显示，武汉市建设防洪工程(0.93)比不建设防洪工程(0.50)效益显著，说明已建的防洪工程发挥了理想的防洪综合效益.

3) 利用层次分析法与灰色区间关联法相结合的评价方法，对城市防洪工程效益评价进行定量与定性分析，研究结果对于指导城市防洪工程的建设与评估具有一定的参考意义.

参考文献
[1] 陆小蕾. 城市防洪安全可变模糊评价模型及其应用研究[D]. 济南: 山东大学, 2011.
Lu Xiaolei. Research on evaluation model and application of variable fuzzy in urban flood safety[D]. Jinan: Shandong University, 2011.
[2] 李昆仑. 层次分析法在城市道路景观评价中的运用[J]. 武汉大学学报(工学版), 2005, 38(1): 143–147.
Li Kunlun. Using analytic hierarchy process in urban road landscape evaluation[J]. Engineering Journal of Wuhan University, 2005, 38(1): 143–147.
[3] 程世丹, 李志刚. 城市滨水区更新中的城市设计策略[J]. 武汉大学学报(工学版), 2004, 37(4): 121–123.
Cheng Shidan, Li Zhigang. Urban design strategy in urban waterfront regeneration[J]. Engineering Journal of Wuhan University, 2004, 37(4): 121–123.
[4] Plate E J. Flood risk and flood management[J]. Journal of Hydrology, 2002, 267(1): 2–11.
[5] SL 206-98已成防洪工程经济效益分析计算及评价规范[S].
Regulation for Economic Benefit Analysis Calculation and Evaluation of Existing Flood Control Projects[S].
[6] GB/T 50805-2012城市防洪工程设计规范[S].
GB/T 50805-2012 Code for Design of Urban Flood Control Project[S].
[7] 谢铁笋, 潘旵, 张建明, 纪昌明. 多目标模糊优选理论在水利工程评标中的应用[J]. 武汉大学学报(工学版), 2002, 35(2): 18–20.
[8] 张炳江. 层析分析法及其应用案例[M]. 北京: 电子工业出版社, 2014.
Zhang Bingjiang. Analytic Hierarchy Process and Application Case[M]. Beijing: Electronic Industry Press, 2014.
[9] 唐东芹, 杨学军, 许东新. 园林植物景观评价方法及其应用[J]. 浙江林学院学报, 2001(4): 64–67.
Tang Dongqin, Yang Xuejun, Xu Dongxin. Study on the method applied in garden plant landscape evaluation[J]. Journal of Zhejiang Forestry College, 2001(4): 64–67.
[10] Saaty T L. How to make a decision: the analytic hierarchy process[J]. European Journal of Operational Research, 1990, 48(1): 9–26. DOI:10.1016/0377-2217(90)90057-I
[11] 罗党. 灰色决策问题的分析方法研究[D]. 南京: 南京航空航天大学, 2004.
Saaty T L. How to make a decision: the analytic hierarchy process[J]. European Journal of Operational Research, 1990, 48(1): 9-26.
[12] Yang Jihui, Cao Bingyuan. Fuzzy geometric programming and its application[J]. Fuzzy Inf, 2010(1): 101–112.
[13] 刘涛, 邵东国, 顾文权. 基于层次分析法的供水风险综合评价模型[J]. 武汉大学学报(工学版), 2006, 39(4): 25–28.
Liu Tao, Shao Dongguo, Gu Wenquan. Risk comprehensive evaluation of water supply in middle and lower reaches of Hanjiang River after implementation of middle route of South-to-North Water Diversion[J]. Engineering Journal of Wuhan University, 2006, 39(4): 25–28.
[14] Morss R E, Wilhelmi O V, Downton M W, et al. Flood risk, uncertainty, and scientific information for decision making: lessons from an interdisciplinary project[J]. Bulletin of the American Meteorological Society, 2005, 86(11): 1593–1601. DOI:10.1175/BAMS-86-11-1593
[15] 沈菊琴, 王海霞, 薛亚云, 等. 防洪工程对沿江(河)房地产价值的影响及其量化模型研究[J]. 水利经济, 2007(2): 12–14.
Sheng Juqin, Wang Haixia, Xue Yayun, et al. Effect of flood control works on value of real estate along the rivers and its quantitative model studies[J]. Journal of Economics of Water Resources, 2007(2): 12–14.