文章信息
- 徐箭, 王甜
- XU Jian, WANG Tian
- 交直流混联电力系统的短路容量及电压稳定在线监测方法研究
- Research on short circuit capacity and voltage stability monitoring method of AC/DC hybrid system
- 武汉大学学报 (工学版), 2017, 50(1): 64-68, 96
- Engineering Journal of Wuhan University, 2017, 50(1): 64-68, 96
- http://dx.doi.org/10.14188/j.1671-8844.2017-01-009
-
文章历史
- 收稿日期: 2016-06-15
与交流系统相比,直流输电系统具有输电容量大、损耗小、投资成本低、有效限制短路电流、功率可控及可改善系统稳定性等优势,目前直流输电系统在电力系统中的应用日益广泛[1].随着实际电网中越来越多的直流线路接入交流电网,直流输电系统具有更大的输送容量和灵活性,但也给系统的电压稳定带来了严峻的考验[2].高压直流输电系统接入交流系统后,为受端系统提供有功功率支持的同时,也需要消耗大量的无功功率,从而容易对直流线路两端的交流系统带来电压稳定问题.
对于交流系统中的发电机、变压器、输电线路及负荷这些基本的电力元件,已经建立了相对较为完善的等值电路模型[3],而直流输电系统中含有变流、滤波等大量的电力电子设备,其控制方式也较为复杂[4-7],因此,目前还没有对直流系统建立适用于交流系统分析的较为完善的等值电路,难以运用现有交流系统中分析电压稳定的方法来研究交直流混联系统中的电压稳定问题.在常规电力系统分析中,对直流系统建模需要考虑换流器、交直流网络、交直流系统的接口和直流系统控制等模型[8, 9].目前常用的方法是把交流系统和直流系统分别处理,通过换流器连接,交流系统采用相量模型,直流系统采用电阻、惯性环节或电磁暂态模型[10, 11].这种对直流系统的建模方式,使得交直流混联系统等值模型较为复杂,在应用交流系统中经典的稳定分析理论对其进行计算及仿真分析时变得十分困难,而直接将直流系统等值为换流母线上的等值负荷,交流系统则为直流系统提供等值电压源,则无法考虑直流系统在实际动态运行中的变化对交流系统的影响.文献[12]提出了一种基于相量测量单元的直流线路等值电路,该等值方法利用安装在直流线路两端交流母线上的PMU的测量信息,包括电压和电流相量,将直流线路等值为简化的“Γ”形等值电路,该等值电路由整流侧交流母线对地支路及接于该母线与逆变侧交流母线间的支路构成,等值后的交直流混联系统就成为一个纯交流系统,可用交流电路中的理论及分析方法研究其电压稳定性.
本文基于文献[12]提出的直流线路等值方法,利用PMU量测信息将直流线路等值为适用于交流系统分析中的等值阻抗网络,从而将交直流混联系统转化为单纯的交流系统,并运用交流系统中基于短路容量的电压稳定分析方法,研究了交直流混联系统的电压稳定问题.
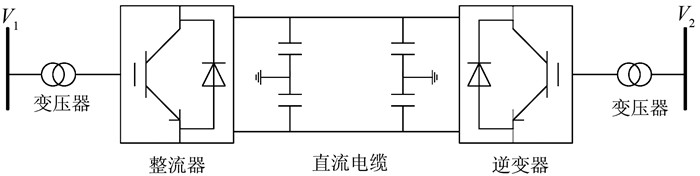
1 基于PMU量测的直流等值建模 1.1 基于电路理论的直流等值模型图 1是一条常规的直流输电线路的结构示意图.
|
| 图 1 直流输电线路结构示意图 Figure 1 Sketch of DC transmission line |
以直流线两端的整流器和逆变器为分界点,画出从整流侧交流母线至逆变侧交流母线的准稳态模型,如图 2所示.

|
| 图 2 直流输电线路准稳态模型 Figure 2 Quasi-steady-state model of DC transmission line |
变流器两端交流母线和直流母线电压幅值具有以下关系:
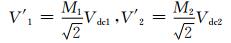 (1)
(1)
式中:M1、M2为整流侧及逆变侧变流器的调制比.
由换流器直流侧母线及直流电阻构成的电路的电压方程为
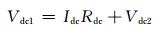 (2)
(2)
根据式 (1)、(2),消去直流侧母线电压Vdc1、Vdc2,得到各变流器交流侧母线电压幅值间关系式:
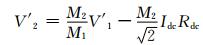 (3)
(3)
式中:电压相量V′1、V′2,电流相量Idc相角均为逆变侧交流母线电压相角δ2.
直流线路准稳态模型可简化为一个二端口交流网络.这是一个含有电压源支路的无源网络,根据交流电路理论中的替代原理,无源网络中的任意一条支路都可以用具有相同电压和电流的阻抗支路代替,同时考虑表征变流器两端的平波电抗器及开关损耗的阻抗Z1、Z2,该二端口网络可进一步简化为只含有阻抗支路的等值电路.由于消耗在Z1上的电压损耗较小,电路中代表变流侧交直流母线电压关系的对地支路可前移至平波电抗器之前的节点处,直流系统最终等值为如图 3所示的“Γ”形等值电路[12].

|
| 图 3 直流输电线路“Γ”形等值电路 Figure 3 Γ-shaped equivalent circuit of DC transmission line |
假设在直流线路两侧交流母线上均装有PMU装置,则可以测得上述等值电路中的电压相量V1、V2和电流相量I1、I2.根据基尔霍夫定律,等值电路中的ZE1、ZE2可根据下式计算得到:
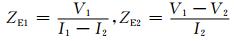 (4)
(4)
在该辨识方法中,并没有对直流系统中的动态响应及控制策略进行详细建模,但其影响却能够通过等值电路中随时间变化的各阻抗值反映出来.
2 基于短路容量的电压稳定分析方法 2.1 短路容量的计算方法短路容量直接反映了节点的电压稳定水平,较大的短路容量值表明节点电压稳定性好,相反,较小的短路容量值则表明该节点电压稳定水平较差.
根据短路容量的定义,对于图 4所示的戴维宁等值电路,负荷节点的短路容量可表示为系统戴维宁等值电势幅值与戴维宁等值阻抗幅值的比值[13],进一步推导可知,短路容量可以利用系统各电势源的内电势以及各电源点对短路点的转移阻抗来计算.

|
| 图 4 戴维宁等值电路 Figure 4 Thevenin equivalent circuit |
对一个有多个电源的线性网络,根据叠加原理,可以把负荷节点的短路容量表示成:
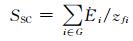 (5)
(5)
式中:G是有源支路的集合;Ėi为第i个有源支路的电势;zfi为电势源i对负荷节点的转移阻抗.
利用节点阻抗矩阵可以方便地计算式 (5) 中的转移阻抗:
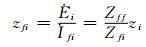 (6)
(6)
同时,利用式 (6) 计算得到的各电源节点对负荷节点的转移阻抗后,可以计算得到负荷节点的戴维宁等值阻抗Z和戴维宁等值电势E:
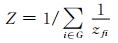 (7)
(7)
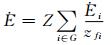 (8)
(8)
具体计算过程中,可根据网络参数列写该网络的节点导纳矩阵,对其求逆,得到节点阻抗矩阵,利用上述方法,计算各电势源对短路点的转移阻抗,并利用PMU量测的各电势源的内电势,计算出该点的戴维宁等值参数及对应的短路容量值.
2.2 基于短路容量的电压稳定裕度指标对于图 4所示的戴维宁等值电路,负荷节点电压稳定裕度指标 (Voltage Stability Index,VSI) 与负荷功率以及戴维宁等值参数之间的关系如下式所示 (具体推导过程详见文献[14]):
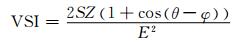 (9)
(9)
式中:E为戴维宁等值电势;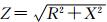
当0 < VSI < 1时,节点电压是稳定的,且该指标值越小表明电压的稳定裕度越大.当VSI=1时,节点电压是临界稳定.当VSI>1时,节点电压不稳定.因此,可以根据负荷节点的戴维宁等值参数及其负荷功率值来在线计算,并评估负荷节点的电压稳定程度.
2.3 基于直流参数辨识的负荷母线短路容量在线计算及电压稳定监测当交流系统内接入直流线路时,根据2.1节中对于直流线路的等值方法,直流线路等值简化为“Γ”形等值电路,直流线路本身不同于交流线路的特征就会在“Γ”形等值电路的等值参数上体现出来,从而改变整个系统的网络参数和负荷节点的短路容量,从而影响电压稳定性.
因此,可以通过直流线路两侧PMU量测信息在线辨识直流线路的等值模型参数,然后修正各电源节点对负荷节点的转移阻抗,按照式 (5) 计算短路容量,根据式 (8) 计算其电压稳定裕度指标,从而分析直流接入对交流系统电压稳定性的影响.
3 仿真结果及分析 3.1 直流等值模型仿真验证IEEE 39节点标准测试系统是一个纯交流系统,其系统接线图如图 5所示.
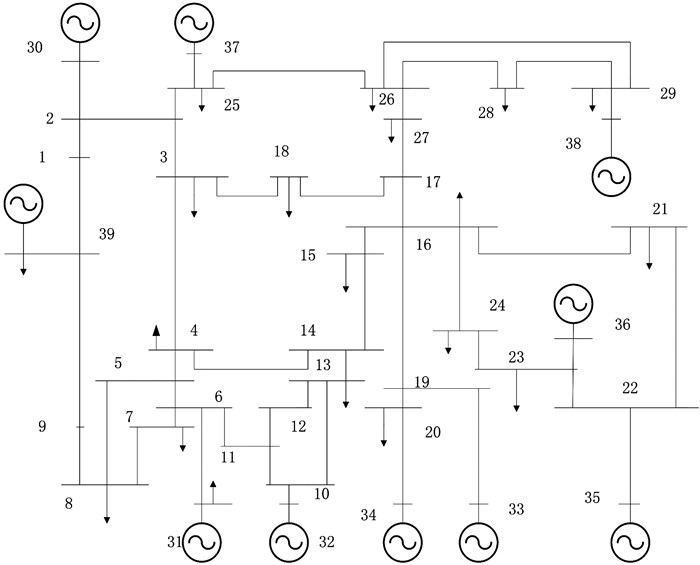
|
| 图 5 IEEE 39节点系统接线图 Figure 5 Line diagram of IEEE 39-bus system |
为了验证上述直流线路等值方法的有效性,将该系统中的25~26、18~17、14~15这3条交流线路断开,将整个系统分成2个独立的交流系统,作为直流输电的送端系统 (区域1) 和受端系统 (区域2).根据线路断开前输送的有功功率,在25号节点与26号节点之间接入一条直流线路代替原有的交流线路,设置直流线路的直流电流,使直流线输送有功功率与断开前的交流线路相等,形成交直流混联系统.
计算出接入直流线路后系统的潮流,得到系统中各交流母线的电压相量.根据交流网络的参数信息及潮流计算得到的25、26号母线的电压相量,计算出直流线路两端交流侧的电流相量,作为PMU的测量信息,然后进行直流线路等值参数辨识,得到直流线路等值结果,如表 1所示.
| 编号 | 电压 | 电流 | 直流线路等值阻抗 |
| 25 | 1.08∠-3.11° | 3.17∠47.5° | ZE1=-0.0115-j0.2129 |
| 26 | 1.10∠3.86° | 3.47∠-51.9° | ZE2=0.0274-j0.0268 |
| 注:基值为100 MVA,345 kV;电压、电流幅值及等值阻抗为标幺值. | |||
以系统中各母线电压幅值及其相角作为状态量,计算等值后系统的潮流,比较等值前后的潮流计算结果,以验证该直流线路等值方法的有效性.区域1内各母线电压幅值在等值前后的计算结果如表 2所示.
| 母线名 | 直流模型 | 等值模型 | |||
| 电压幅值 | 电压相角/(°) | 电压幅值 | 电压相角/(°) | ||
| 1 | 1.0529 | -6.5971 | 1.0529 | -6.5946 | |
| 10 | 1.0177 | -3.9789 | 1.0177 | -3.9775 | |
| 11 | 1.0136 | -4.8848 | 1.0136 | -4.8834 | |
| 12 | 1.0008 | -4.7948 | 1.0008 | -4.7934 | |
| 13 | 1.0146 | -4.5996 | 1.0146 | -4.5981 | |
| 14 | 1.0114 | -6.0303 | 1.0114 | -6.0288 | |
| 18 | 1.0408 | -6.4490 | 1.0408 | -6.4465 | |
| 2 | 1.0636 | -3.7919 | 1.0636 | -3.7888 | |
| 25 | 1.0801 | -3.1137 | 1.0800 | -3.1095 | |
| 3 | 1.0411 | -6.114 | 1.0411 | -6.1116 | |
| 30 | 1.0475 | -1.4060 | 1.0475 | -1.4029 | |
| 31 | 0.9820 | 0 | 0.9820 | 0 | |
| 32 | 0.9831 | 4.0128 | 0.9831 | 4.0143 | |
| 37 | 1.0278 | 4.7942 | 1.0278 | 4.7987 | |
| 39 | 1.0300 | -8.3239 | 1.0300 | -8.3218 | |
| 4 | 1.0070 | -7.8658 | 1.0070 | -7.8641 | |
| 5 | 1.0072 | -7.2372 | 1.0072 | -7.2358 | |
| 6 | 1.0093 | -6.6511 | 1.0093 | -6.6498 | |
| 7 | 0.9987 | -8.7667 | 0.9987 | -8.7654 | |
| 8 | 0.9977 | -9.2306 | 0.9977 | -9.2293 | |
| 9 | 1.0289 | -8.7303 | 1.0289 | -8.7285 | |
| 注:基值为345 kV;电压幅值为标幺值. | |||||
从表 2中可以看出,对直流线路等值后,其潮流计算的结果和实际直流线路接入系统时的潮流计算结果十分接近,节点电压幅值的最大相对误差分别为0.113%和0.059%,电压相角的最大相对误差为0.679%和0.789%,说明该直流线路等值方法是有效的,可以应用该等值系统进行交直流混联系统的短路容量和电压稳定分析.
3.2 直流接入对系统短路容量的影响从3.1节中直流线路的等值阻抗结果可以看出,ZE1所在的对地支路,其阻抗实部均为负数,可将其视为恒阻抗负荷,ZE2所在支路,可视作一条交流输电线路.常规交流输电线路接近于电感性支路,其阻抗角接近90°,而对于直流等值线路,其虚部为负值,呈电容性支路,故直流的接入会改变交流系统网络结构参数,影响各节点的戴维宁等值阻抗,进而影响其短路容量.图 6、7为接入直流前后区域1和区域2内母线短路容量的变化情况.
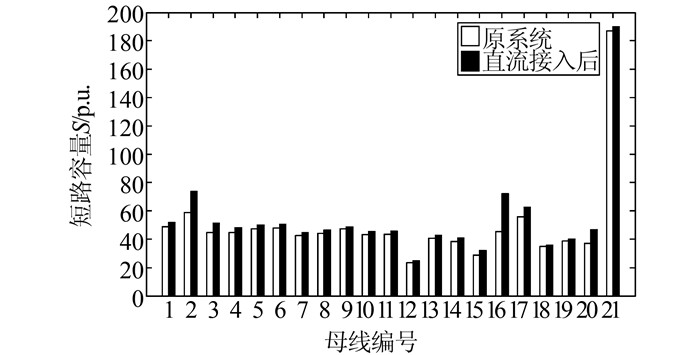
|
| 图 6 区域1内各母线短路容量变化 Figure 6 The variation of SCC in area 1 |
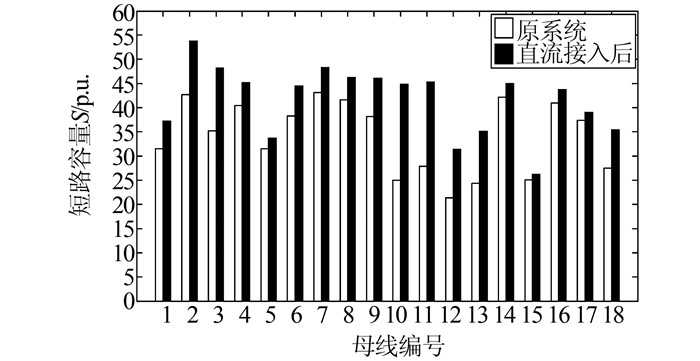
|
| 图 7 区域2内各母线短路容量变化 Figure 7 The variation of SCC in area 2 |
从图中可以看出,接入直流线路后加强了区域1和区域2两个交流系统之间的电气联系,故两个区域内母线短路容量较接入直流线路前都增大,由于功率由区域1流向区域2,受端区域2内母线短路容量的增加更为明显.
3.3 直流接入对系统电压稳定性影响表 3列出了直流接入前后,各节点电压稳定裕度指标的变化情况.
| 母线编号 | 直流接入前 | 直流接入后 |
| 3 | 0.048 01 | 0.046 38 |
| 4 | 0.328 10 | 0.315 00 |
| 7 | 0.160 70 | 0.156 00 |
| 8 | 0.337 80 | 0.328 30 |
| 12 | 0.150 00 | 0.143 80 |
| 18 | 0.045 11 | 0.040 41 |
| 25 | 0.138 80 | 0.103 90 |
| 31 | 0.008 63 | 0.008 43 |
| 39 | 0.148 00 | 0.147 30 |
| 15 | 0.332 20 | 0.304 10 |
| 16 | 0.238 10 | 0.220 70 |
| 20 | 0.481 90 | 0.470 60 |
| 21 | 0.219 20 | 0.203 50 |
| 23 | 0.168 90 | 0.161 00 |
| 24 | 0.212 20 | 0.153 70 |
| 26 | 0.131 10 | 0.118 60 |
| 27 | 0.632 90 | 0.479 90 |
| 28 | 0.229 10 | 0.203 90 |
| 29 | 0.264 20 | 0.239 50 |
由表 3可知,直流线路接入前,系统中各负荷节点的电压稳定指标均小于1,节点电压稳定;接入直流线路后,由于直流线路等值阻抗对系统各负荷节点的短路容量的影响,使得各负荷节点的电压稳定指标值均有不同程度减小,根据2.2节分析,直流接入系统后使各负荷节点电压稳定裕度增大,有利于保持系统电压稳定,说明利用该思路研究直流接入对交流系统电压稳定的影响,进而实现电压稳定指标在线计算是可行的.
4 结论交直流混联系统中,直流的接入对系统短路容量产生影响,从而影响了基于短路容量的负荷节点电压稳定指标值,使直流接入后的系统负荷节点电压稳定裕度增大.在直流输电技术越来越广泛地应用于电力系统的趋势下,研究直流的接入对交流系统电压稳定的影响具有十分重要的意义,本文利用将直流线路等值为交流系统中的电力元件的方法,从短路容量的角度分析电力系统中负荷母线电压稳定,计算节点电压稳定指标,实现对负荷母线电压稳定裕度的在线监测,为进一步研究交直流混联系统电压稳定提供了一种新思路.
| [1] |
韩显芳.交直流受端电网电压稳定性研究[D].济南:山东大学, 2013:1-9.
Han Xianfang. Research on voltage stability of AC/DC power system[D]. Jinan: Shandong University, 2013:1-9. |
| [2] |
刘天琪.
现代电力系统分析理论与方法[M]. 北京: 中国电力出版社, 2007: 69-70.
Liu Tianqi. Modern Power System Analysis Theory and Method[M]. Beijing: Chinese Electric Power Press, 2007: 69-70. |
| [3] |
何仰赞, 温增银.
电力系统分析[M]. 武汉: 华中科技大学出版社, 2002: 11-26.
He Yangzan, Wen Zengyin. Electric Power System Analysis[M]. Wuhan: Huazhong University of Science and Technology Press, 2002: 11-26. |
| [4] |
程鲁文.交直流混联系统送受端规模对电力系统稳定性影响[D].广州:华南理工大学, 2012:1-11.
Cheng Luwen. Study on the stability of AC/DC combined power system between reception and transmission scale[D]. Guangzhou: South China University of Technology, 2012:1-11. |
| [5] |
吴红斌, 丁明, 李生虎. 直流输电模型和调节方式对暂态稳定影响的统计研究[J].
中国电机工程学报, 2003(10): 32–37.
Wu Hongbin, Ding Ming, Li Shenghu. Statistical research on the effects of HVDC models and controls to transient stability of power system[J]. Proceedings of the CSEE, 2003(10): 32–37. |
| [6] |
孙国强, 李育燕, 卫志农, 叶芳. 含VSC-HVDC的交直流混合系统状态估计[J].
电力自动化设备, 2010(9): 7–12.
Sun Guoqiang, Li Yuyan, Wei Zhinong, Ye Fang. State estimation of power system with VSC-HVDC[J]. Electric Power Automation Equipment, 2010(9): 7–12. |
| [7] |
何智文.交直流混合电力系统无功优化模型及线性优化算法[D].广州:华南理工大学, 2013:7-14.
He Zhiwen. Reactive power optimation model and linear programming algorithm in AC/DC hybrid power systems[D]. Guangzhou: South China University of Technology, 2013:7-14. |
| [8] |
毛晓明, 张尧, 张艳. 高压直流建模研究的相关问题[J].
电力自动化设备, 2007(12): 14–17.
Mao Xiaoming, Zhang Yao, Zhang Yan. Survey on HVDC system modeling[J]. Electric Power Automation Equipment, 2007(12): 14–17. |
| [9] |
Kunder P.电力系统稳定与控制[M].周孝信, 宋永华, 李兴源, 等, 译.北京:中国电力出版社, 2002:130-141.
Kunder P. Power System Stability and Control[M]. Translated by Zhou Xiaoxin, Song Yonghua, Li Xingyuan, et al. Beijing: Chinese Electric Power Press, 2002:130-141. |
| [10] | Flourentzou N, Agelidis V G, Demetriades G D. VSC-based HVDC power transmission systems: An overview[J]. IEEE Trans. Power Electron, 2009, 24(3): 592–602. DOI:10.1109/TPEL.2008.2008441 |
| [11] | Abbas A M, Lehn P W. PWM based VSC-based VSC-HVDC systems-A review[C]// Proc.2009 IEEE PES General Meeting, 2009:1-9. |
| [12] | He L, Liu C C. Parameter identification with PMUs for instability detection in power systems with HVDC integrated offshore wind energy[J]. IEEE Trans. Power Syst., 2014, 29(2): 775–784. DOI:10.1109/TPWRS.2013.2283656 |
| [13] | Taylor C W. Power System Voltage Stability[M]. New York: McGraw-Hill, 1994: 9-10. |
| [14] |
邓桂平.基于短路容量的电压稳定研究[D].武汉:武汉大学, 2009:71-83.
Deng Guipin. Research on voltage stability of power system based on short circuit capacity[D].Wuhan:Wuhan University, 2009:71-83. |
 2017, Vol. 50
2017, Vol. 50



