武汉大学学报(工学版)   2016, Vol. 49 Issue (1): 27-31

文章信息

范杨臻, 杨国录, 夏倩, 骆文广, 祁明
FAN Yangzhen, YANG Guolu, XIA Qian, LUO Wenguang, QI Ming
分布式陆面-水文模型在淮河流域的应用
Application of distributed land surface-hydrological model to Huaihe Basin
武汉大学学报(工学版), 2016, 49(1): 27-31
Engineering Journal of Wuhan University, 2016, 49(1): 27-31
http://dx.doi.org/10.14188/j.1671-8844.2016-01-005

文章历史

收稿日期: 2015-04-15
 Abstract              PDF               Figures               Tables
引用本文 0
范杨臻, 杨国录, 夏倩, 骆文广, 祁明. 分布式陆面-水文模型在淮河流域的应用[J]. 武汉大学学报(工学版), 2016, 49(1): 27-31.
FAN Yangzhen, YANG Guolu, XIA Qian, LUO Wenguang, QI Ming. Application of distributed land surface-hydrological model to Huaihe Basin[J]. Engineering Journal of Wuhan University, 2016, 49(1): 27-31.
分布式陆面-水文模型在淮河流域的应用
范杨臻1,2,3, 杨国录1,2, 夏倩4, 骆文广1,2, 祁明5     
1. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;
 2. 武汉大学污淤泥研究中心，湖北 武汉 430072;
 3. 湖北省水利水电科学研究院，湖北 武汉 430070;
 4. 科隆大学地球物理和气象研究所, 德国 科隆 50923;
 5. 武汉清泓科技有限责任公司，湖北 武汉 430072
收稿日期: 2015-04-15
作者简介: 范杨臻(1987-)，男，博士研究生，主要从事水环境模拟及流域水循环模拟研究， E-mail：fyzxq1987@163.com.
通讯作者: 杨国录(1955-)，男，教授，博士生导师，主要从事流域水环境治理研究， E-mail：ygl516@sina.com
基金项目: “十二五”国家水体污染控制与治理科技重大专项基金资助项目(编号：2014ZX07104005);国家自然科学基金青年科学基金资助项目(编号：51209162) ;国家自然科学基金资助项目(编号：51279143, 51109167).
摘要: 分布式水文模型是模拟地表径流、研究流域水循环的有效手段，以淮河流域为研究对象，利用数字高程DEM (digital elevation model)、全球植被覆盖数据、土壤结构资料等构建气象数据驱动下的分布式陆面-水文模型，根据1980-1982年淮河流域水文站实测数据进行模型参数率定，采用相对误差、确定性系数和Nash效率系数作为衡量指标来验证模型的模拟精度，并对比淮河流域主要水文站实测逐日径流量与模拟值，分析该模型对洪水流量的模拟效果.研究结果表明，该分布式陆面-水文模型具有较高的模拟精度，能较好地模拟流域水文过程，可用于变化环境下的水循环过程模拟和流域水文响应研究.
关键词： 分布式     陆面-水文模型     流域水文过程    
Application of distributed land surface-hydrological model to Huaihe Basin
FAN Yangzhen1,2,3, YANG Guolu1,2, XIA Qian4, LUO Wenguang1,2, QI Ming5     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. Sewage Sludge & Silt Research Center, Wuhan University, Wuhan 430072, China;
 3. Hubei Water Resources Research Institute, Wuhan 430070, China;
 4. Institute of Geophysics and Meteorology, University of Cologne, Cologne 50923, Germany;
 5. Wuhan Qinghong Science & Technology Co.,Ltd., Wuhan 430072, China
Abstract: The distributed hydrological model is an efficient way for hydrological cycle and surface runoff in catchments. Taking the Huaihe Basin for example, the distributed land surface-hydrological model forced by atmospheric dataset is built with digital elevation model (DEM), global vegetation data, soil structure information, etc. After parameter calibration based on the observation of 1980-1982, relative error, certainty coefficient and Nash coefficient are selected as indices to evaluate the simulation accuracy; and the comparison between daily streamflow measured in Bengbu station and the simulation is carried out to determine the model precision for flood. The results elaborate that this land surface-hydrological model is capable of simulating hydrological processes in a river basin with high accuracy and available to research the drainage basin hydrological cycle and hydrological response to the changing environment.
Key words: distributed     land surface- hydrological model     basin hydrological processes    

作为全球水循环的重要组成部分，气候变化下的陆面水循环及其演变过程对区域乃至全球水循环有着重要影响[1].近年来，计算机技术和3S(GIS、GPS、RS) 技术的进步和广泛应用，可为分布式水文模型提供高精度的流域下垫面数据[2, 3].分布式水文模型能够充分考虑水文过程中的变量与水文响应的时空分布，在研究人类活动和自然环境变化对流域水循环时空过程的影响和区域水资源的演变规律具有独特的优势[4-6].

本文利用遥感和地理信息系统构建数字流域，提取流域特征，以淮河流域为研究对象，采用分布式陆面-水文模型对流域水循环进行数值模拟，并结合实测资料评估模型精度，为流域水循环模拟提供可靠依据.

1 模型构建 1.1 分布式陆面-水文模型

本研究采用的分布式陆面-水文模型由粗网格的陆面模型和细网格的水文模型组成.陆面模型在气象数据的驱动下，进行大气层与地表层的热量、能量及水分交换，包括植被模块、积雪模块、土壤模块等；陆面模型中产流量、蒸散发、下渗量、非饱和层土壤排水量等经空间降尺度[7]、时间升尺度后传递到水文模块，进行流域水文过程模拟，主要包括地表水动力模块、地下水模块和地表水-地下水交互模块.

本研究中，陆面模型采用20 km的计算网格，时间步长为1 800 s；水文模型同样采用20 km的计算网格，时间步长为86 400 s.

1.1.1 陆面模型

植被模块中植被分为树木和草地两层，将通过冠层到地面的贯穿降雨量、叶面滴落量和雪吹落量作为到达地面的降水量；如果地面存在积雪，积雪模型的下层融雪量则作为达到地面的降水量.地表层的热量和水分通量作为积雪模块和土壤模块的输入，模拟非饱和土壤层水分(土壤水)的垂向运动，计算超渗产流量、下渗量、蓄满产流量、非饱和层土壤排水量等[8, 9].

根据表层土壤的土壤特性以及含水量，计算地表下渗容量f*，并结合实际净雨量进一步确定实际下渗量和超渗产流量.

${{f}^{*}}={{K}_{s}}*{{\psi }_{s}}*b*\left( \frac{1-{{\theta }_{1}}/{{\theta }_{s}}\ }{0.5{{z}_{1}}} \right)+{{K}_{s}}$

式中：ks为饱和水力传导度；ψs为饱和土壤吸力；θs为孔隙度；θ1为表层土壤含水率;z1为表层土壤厚度;b为土壤参数.

土壤模型中采用一维非饱和流达西定律描述土壤水的垂向运动[10]，并结合地下水水位高程实现非饱和土壤的动态分层.

$\frac{\partial \theta }{\partial t}=\frac{\partial }{\partial z}\left( D\left( \theta \right)\frac{\partial \theta }{\partial z} \right)-\frac{\partial K\left( \theta \right)}{\partial z}-{{q}_{s}}$

其中：θ 为土壤含水率；K(θ)为土壤导水率，K(θ)=Ksθ/θs2b+3；D(θ)为水力扩散系数，由D(θ)=K(θ)∂ψ/∂θ和ψ(θ)=ψs(θ/θs)－b计算；qs为源汇项.

土壤水分入渗再分配后，多余的土壤水分被“挤”向上一层，而超过表层土壤蓄水能力的水分将作为蓄满产流量重返地表，在水文模式中参与汇流计算.

1.1.2 水文模型

水文模型用于模拟流域水文过程，包括地表水、地下水、河湖-地下水体交互模块3个子模块，分别模拟坡面流和河湖径流、地下水运动、地表水体与地下水体的交换[11-13].

地表水模块采用D8流向算法[14]计算单元网格的坡面汇流，由DEM数据生成河网，采用曼宁公式计算流速v，并根据水量平衡计算河网汇流.

$\upsilon =\frac{m}{n}*{{R}^{\frac{2}{3}}}*{{J}^{\frac{1}{2}}}$

式中：n为曼宁系数；R为水力半径；J为水力坡度；m为转换系数.

$\frac{dh}{dt}={{q}_{in}}-{{q}_{out}}$

其中：h为坡面流/河道水深；qin是入流量，包括水面净雨量、坡面入流、上游来水量、地下水对河道的补给量；qout为出流量，主要有水面蒸发量、下游出流量、渗漏量.

地下水模块将含水层视为底部封闭的单元体，假定地下水面以上非饱和土壤含水量在垂直剖面上保持连续，且通过垂向水分扩散和重力排水相互作用达到平衡.该模块中地下水的运动遵循二维Boussinesq方程，计算公式如下：

$s\cdot \frac{\partial H}{\partial t}=\frac{\partial }{\partial x}\left( {{T}_{x}}\cdot \frac{\partial H}{\partial x} \right)+\frac{\partial }{\partial y}\left( {{T}_{y}}\cdot \frac{\partial H}{\partial y} \right)+{{q}_{s}}$

式中：H为地下水水头；s为蓄水系数，Tx/Ty分别为x/y方向上的导水系数；qs为源汇项.

河湖-地下水体交互模块用于模拟河湖等地表水体与土壤水、地下水的相互作用，水分通量根据Darcy定律计算.单元网格的河道与地下水之间存在弱透水层，因此只考虑河床底部与地下水/土壤水的水分通量，不考虑河流侧边界的水分通量.

$q=k\cdot \frac{\Delta h}{\Delta x}$

式中：q为交互界面水分通量；k为导水系数；Δh为水头差.

1.2 模拟流程

该模型可用于流域水循环模拟和水文预报，主要包括数据前处理、模型耦合、模型运行和模型校验4个部分(如图 1所示).

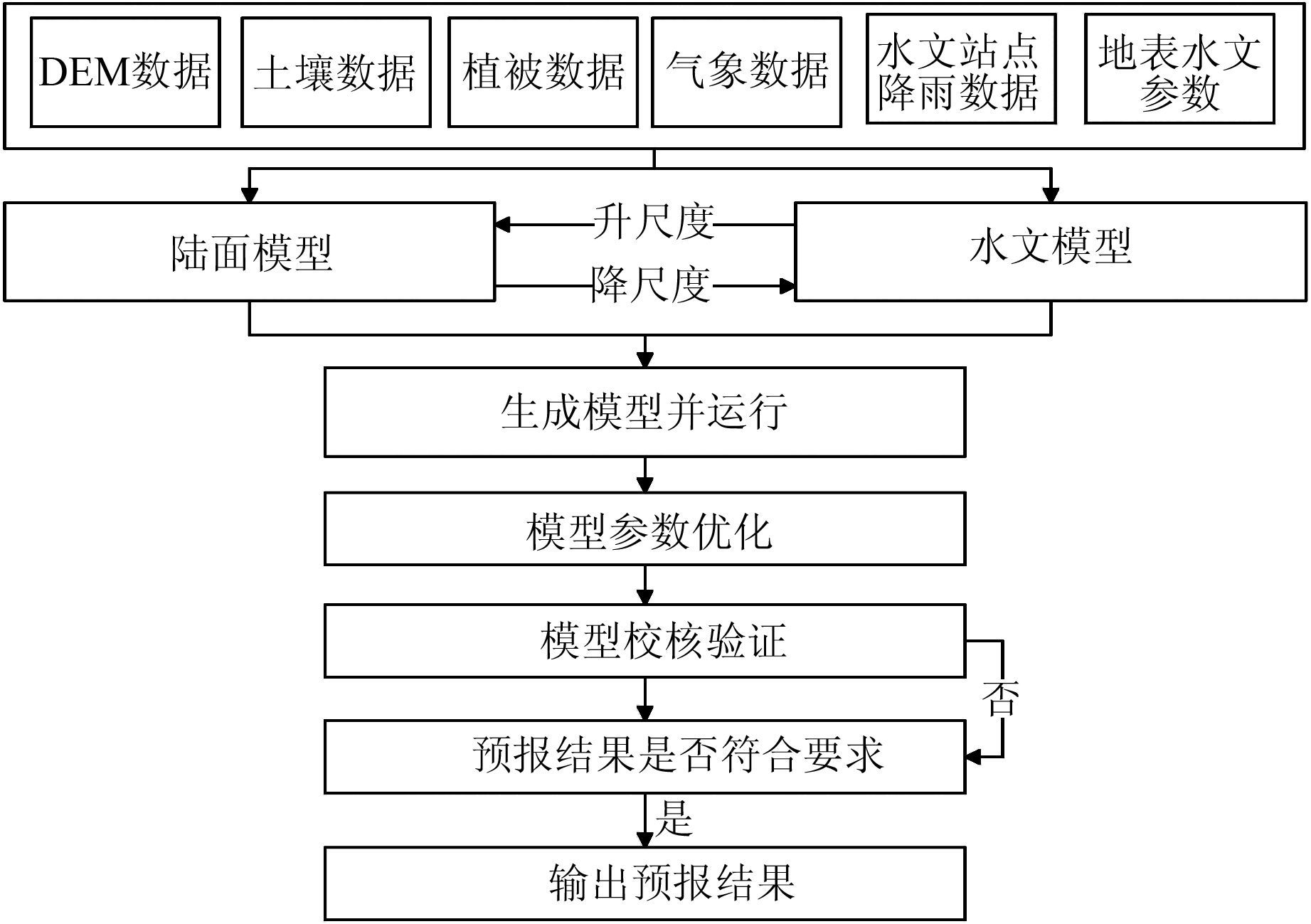
图 1 计算流程图 Figure 1 Flow chart for simulation
图选项
2 模型应用 2.1 研究区域概况

淮河流域位于我国东部南北气候过渡带，属于温带湿润季风气候区，流域面积约27万 km2，地理范围为东经111°55′~121°25′，北纬30°55′~36°36′，流域内西部及西南部多为山区、丘陵区，其余为平原.区域多年平均降雨量920 mm，降雨主要集中在5-8月，该时段降雨量占全年的65%；6月中旬至7月上旬，进入梅雨季节，降雨量大且范围广，容易造成流域性大洪水.降水年际变化很大，多雨年与少雨年的降水量比值可达3~5倍.淮河流域水系及水文站如图 2所示.

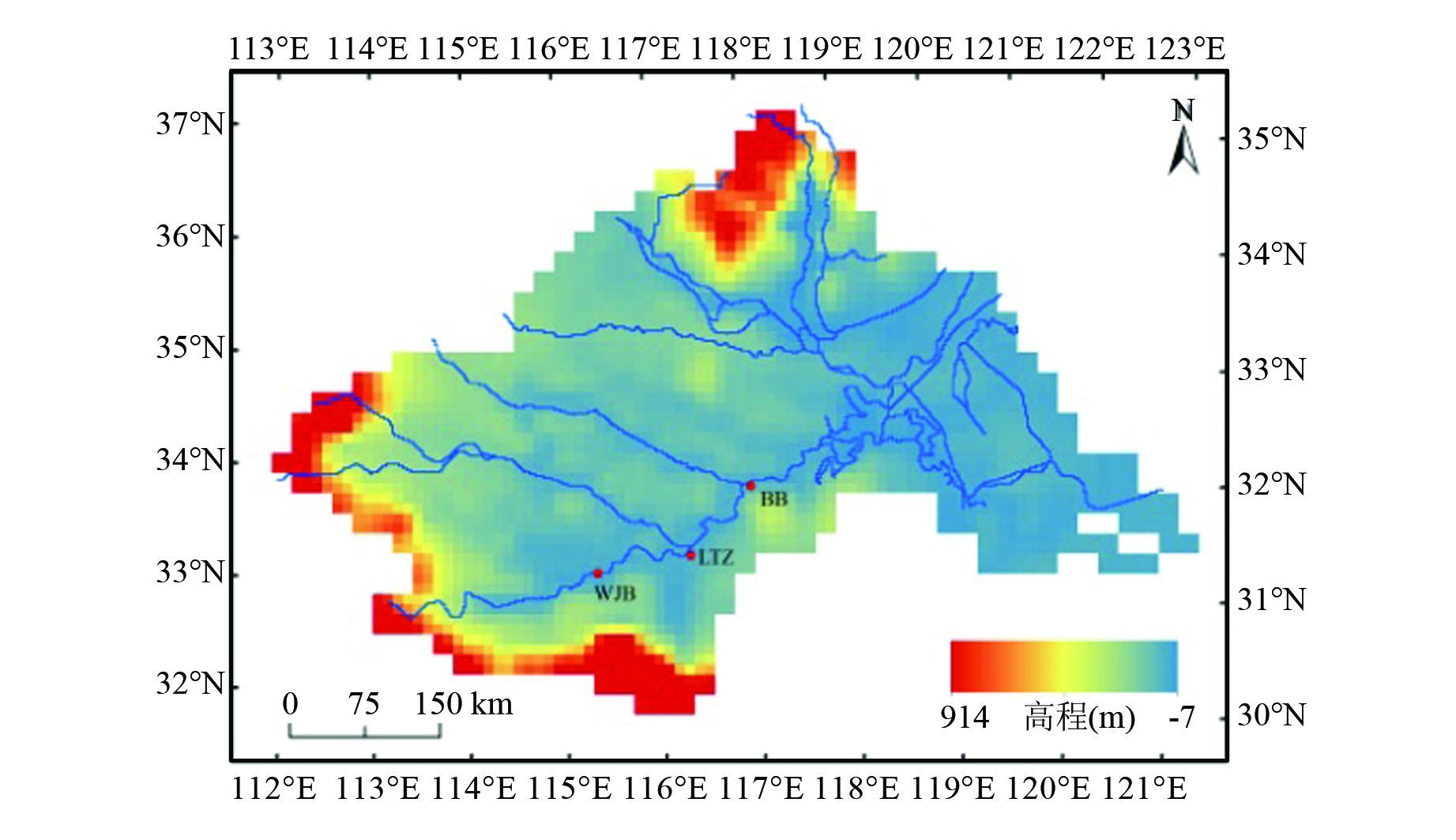
图 2 研究区域水系及水文站 Figure 2 Location of hydrological stations and river system in the Huaihe Basin
图选项
2.2 流域空间信息

本研究的地形数据采自全球HYDRO1K DEM数据库，分辨率为1 km；植被数据采用分辨率2度的全球植被覆盖数据，共包括12种植被覆盖类型；土壤结构资料来自全球STATSGO 2°×2°数据库.

2.3 气象数据

气温、气压、湿度等气象数据来自NCEP/NCAR再分析资料，该数据具有T62的空间分辨率和6 h时间步长.降雨数据是影响陆面水文循环过程的重要因素，本研究采用水文站站网实测降雨数据，并进行流域范围的降水空间插值.

2.4 水文过程模拟 2.4.1 参数率定

分布式水文模型的参数具有明确的物理意义，均可通过野外观测数据确定.但对时空变化较大的面域，基于测量点获取的数据代表性不足，因此实际模拟时仍需进行参数率定.本文基于各个参数的物理意义，在参数取值范围内调整数值从而优化模拟结果(见表 1)[15, 16].

表 1 模型参数 Table 1 Model parameters
类别 参数 获取方法
地表和植被参数 植被类型 实测数据
植被覆盖系数 实测数据
表层土壤类型 实测数据
土壤水分参数 黏土含量与砂土含量 实测数据
土壤饱和含水率与饱和导水率 参考STATSGO全球土壤数据库
河道参数 河道深度 实测数据
流域范围 实测数据
气象参数 降雨量 实测数据
地表气压与风向 实测数据
其他参数 融雪指数水力传导度与含水层厚度 实测获得，本文需率定
表选项

本文选取洪峰流量相对误差、确定性系数和Nash效率系数[5]作为评价模型精度的指标.确定性系数(R2)和Nash效率系数(Cd)可反映洪水流量过程模拟值与实测值之间的吻合度，其计算公式如下：

${{R}^{2}}=\frac{{{\left( \sum{\left( {{Q}_{0}}-\overline{{{Q}_{0}}} \right)\left( {{Q}_{s}}-\overline{{{Q}_{s}}} \right)} \right)}^{2}}}{\sum{{{\left( {{Q}_{0}}-\overline{{{Q}_{0}}} \right)}^{2}}\sum{{{\left( {{Q}_{s}}-\overline{{{Q}_{s}}} \right)}^{2}}}}}{{C}_{d}}=1-\frac{\sum{{{\left( {{Q}_{0}}-{{Q}_{s}} \right)}^{2}}}}{\sum{{{\left( {{Q}_{0}}-{{{\bar{Q}}}_{0}} \right)}^{2}}}}$

式中：Q0为实测值，m3/s；Qs为模拟值，m3/s；Q0为实测平均值，m3/s；Qs为模拟值的平均值，m3/s.R2和Cd计算值范围均在0~1之间，越接近1表明模拟效果越好.

本文选用淮河流域1980-1987年逐日流量模拟结果与实测流量进行比较，其中1980-1982年用于参数率定，采用1983-1987年数据进行模拟效果检验.率定期和校验期的模拟结果分析见表 2.

表 2 率定期和校验期的洪水模拟结果 Table 2 Statistic results of simulated flood in calibration periods and validation periods
日期 流量/(m3\5s-1) 相对误差/% 确定系数 Nash效率系数
模拟 实测
率定期(19801012) 1 612 1 690 6.46 0.92 0.86
率定期(19810220) 622 629 1.06 0.85 0.76
率定期(19820603) 245 219 -12.05 0.88 0.61
率定期(19821203) 1 036 981 -5.63 0.95 0.84
校验期(19850514) 3 158 3 390 -6.81 0.93 0.90
校验期19860503) 461 446 3.42 0.84 0.74
表选项
2.4.2 模拟验证

由模拟结果可知，蚌埠断面模拟流量与实测值对应较好，计算所得的洪水形状与实测基本一致，流量模拟值与实测值的比较如图 3所示.统计分析结果表明，计算流量与实测流量吻合程度较高，确定性系数达0.84~0.95，Nash效率系数达0.61~0.90.由此可见，本模型的模拟值与实测值吻合效果较好，说明该模型在淮河流域具有较高的精度，能较好地模拟淮河流域水文过程.

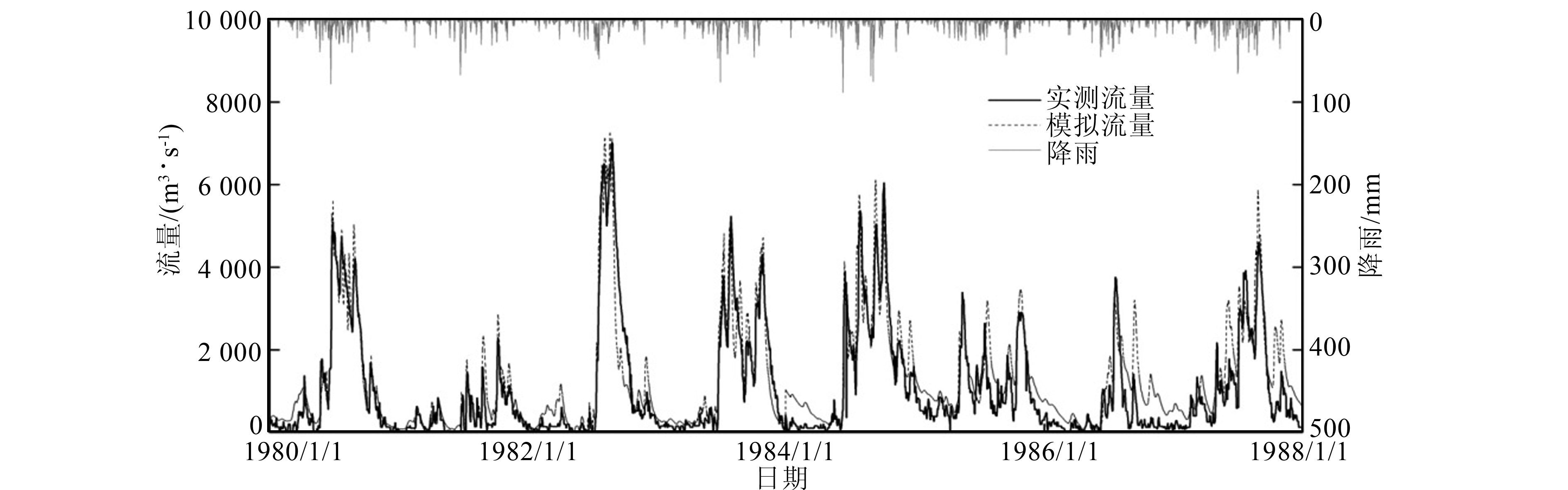
图 3 1980-1987年模拟与实测流量对比图 Figure 3 Discharge comparison of observation and simulation from 1980 to 1987
图选项
3 结论

本文采用气象数据驱动下的分布式陆面-水文模型对淮河流域水循环进行数值模拟，并进行模型模拟结果精度分析，其结果表明，分布式陆面-水文模型对河道流量的模拟与实测值吻合度较好，所建模型合理可信.

参考文献
[1] 徐宗学, 程磊. 分布式水文模型研究与应用进展[J]. 水利学报, 2010, 1(3): 5–6.
Xu Zongxue, Cheng Lei. Progress on studies and applications of the distributed hydrological models[J]. Journal of Hydraulic Engineering, 2010, 1(3): 5–6.
[2] 袁迪, 宋星原, 张艳军. 基于遥感信息的新安江模型参数率定方法[J]. 武汉大学学报(工学版), 2014, 47(1): 23–27.
Yuan Di, Song Xingyuan, Zhang Yanjun. Research on parameter calibration method of Xinanjiang model based on remote sensing information[J]. Engineering Journal of Wuhan University, 2014, 47(1): 23–27.
[3] 杨传国. 区域陆面-水文耦合模拟研究与应用[D].南京:河海大学, 2009.
Yang Chuanguo. Research on coupling land surface-hydrology model and application [D]. Nanjing: Hohai University, 2009.
[4] 包为民. 水文预报[M]. 北京: 中国水利水电出版社, 2006.
Bao Weimin. Hydrologic Forecasting[M]. Beijing: China Water Power Press, 2006.
[5] 熊立华, 郭生练. 分布式流域水文模型[M]. 北京: 中国水利水电出版社, 2004.
Xiong Lihua, Guo Shenglian. Distributed Hydrological Model[M]. Beijing: China Water Power Press, 2004.
[6] 詹道江, 叶守泽. 工程水文学[M]. 北京: 中国水利水电出版社, 2000.
Zhan Daojiang, Ye shouze. Engineering Hydrology[M]. Beijing: China Water Power Press, 2000.
[7] 杨传国, 余钟波, 林朝晖, 等. 大尺度分布式水文模型数字流域提取方法研究[J]. 地理科学进展, 2007, 26(1): 68–76.
Yang Chuanguo, Yu Zhongbo, Lin Zhaohui, et al. Method study of constructing digital watershed for large-scale distributed hydrological model[J]. Progress in Geography, 2007, 26(1): 68–76.
[8] Liang X, Xie Z, Huang M. A new parameterization for surface and groundwater interactions and its impact on water budgets with the variable infiltration capacity (VIC) land surface model[J]. Journal of Geophysical Research: Atmospheres, 2003, 108(D16): 1984–2012.
[9] Yu Z, Lakhtakia M N, Yarnal B, et al. Simulating the river-basin response to atmospheric forcing by linking a mesoscale meteorological model and hydrologic model system[J]. Journal of Hydrology, 1999, 218(1): 72–91.
[10] 孙丽云. 基于非达西渗流的饱和黏土一维固结试验与理论研究[D]. 郑州:郑州大学, 2011.
Sun Liyun. One-dimensional consolidation experiment and theory of saturated clay based on non-Darcy flow[D]. Zhengzhou: Zhengzhou University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10459-1011184813.htm
[11] 张金存, 芮孝芳. 分布式水文模型构建理论与方法述评[J]. 水科学进展, 2007, 18(2): 286–292.
Zhang Jincun, Rui Xiaofang. Discussion of theory and methods for building a distributed hydrologic model[J]. Advances in Water Science, 2007, 18(2): 286–292.
[12] 万民, 熊立华, 董磊华. 飞来峡流域基于栅格 DEM 的分布式水文模拟[J]. 武汉大学学报(工学版), 2010, 43(5): 549–553.
Wan Min, Xiong Lihua, Dong leihua. Grid DEM-based distributed hydrological modeling for Feilaixia watershed[J]. Engineering Journal of Wuhan University, 2010, 43(5): 549–553.
[13] 何姗, 张利平, 夏军, 等. 牛栏江流域径流模拟与实时预报[J]. 武汉大学学报(工学版), 2007, 40(2): 60–64.
He Shan, Zhang Liping, Xia Jun, et al. Research on simulation and real-time forecasting of runoff of Niulanjiang basin[J]. Engineering Journal of Wuhan University, 2007, 40(2): 60–64.
[14] 秦承志, 李宝林, 朱阿兴, 等. 水流分配策略随下坡坡度变化的多流向算法[J]. 水科学进展, 2006, 17(4): 450–456.
Qin Chengzhi, Li Baolin, Zhu Axing, et al. Multiple flow direction algorithm with flow partition scheme based on downslope gradient[J]. Advances in Water Science, 2006, 17(4): 450–456.
[15] 王家虎. 分布式水文模型理论与方法研究[D].南京:河海大学, 2006.
Wang Jiahu. Study on theory and method of DHM[D]. Nanjing: Hohai University, 2006.
[16] 余钟波. 流域分布式水文学原理及应用[M]. 北京: 科学出版社, 2008.
Yu Zhongbo. Principle & Application of Distributed Hydrological Model[M]. Beijing: Science Press, 2008.