武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 621-626

文章信息

杨秀萍, 张喆, 郝淑英
YANG Xiuping, ZHANG Zhe, HAO Shuying
覆冰四分裂导线动态气动力特性分析
Dynamic aerodynamic characteristics of iced quad bundled conductors
武汉大学学报(工学版), 2016, 49(4): 621-626
Engineering Journal of Wuhan University, 2016, 49(4): 621-626
http://dx.doi.org/10.14188/j.1671-8844.2016-04-023

文章历史

收稿日期: 2015-04-22
 Abstract              PDF               Figures               Tables
引用本文 0
杨秀萍, 张喆, 郝淑英. 覆冰四分裂导线动态气动力特性分析[J]. 武汉大学学报(工学版), 2016, 49(4): 621-626.
YANG Xiuping, ZHANG Zhe, HAO Shuying. Dynamic aerodynamic characteristics of iced quad bundled conductors[J]. Engineering Journal of Wuhan University, 2016, 49(4): 621-626.
覆冰四分裂导线动态气动力特性分析
杨秀萍1,2, 张喆2, 郝淑英2     
1. 天津理工大学天津市先进机电系统设计与智能控制重点实验室，天津 300384;
 2. 天津理工大学机械工程学院，天津 300384
收稿日期: 2015-04-22
作者简介: 杨秀萍(1962-)，女，教授，硕士研究生导师，主要从事流体传动及有限元应用研究，E-mail:yhp420@sina.com.
基金项目: 天津市自然科学基金资助项目(编号：11JCYBJC05800).
摘要: 为研究覆冰分裂导线舞动时的气动力特性，基于Fluent软件的用户自定义函数对导线的舞动轨迹进行编程并结合动网格技术实现流固耦合.计算了新月形覆冰四分裂导线横向振动时的动态气动力系数，并与静态模拟结果进行比较；分析了舞动幅值和频率对动态气动力的影响.结果表明：相同风速下，动态气动力系数大于静态值，二者具有相同的变化规律；舞动时，迎风侧子导线尾流偏移，对背风侧子导线的影响减小，使背风侧子导线的动态气动力系数比静态时明显增加；阻力、升力系数随舞动幅值和频率的增加而增大，但频率对动态气动力的影响小于幅值的影响；工程中预测大档距导线舞动引起的断线临界风速和塔承受的荷载时，应考虑动态气动力系数对舞动的影响.
关键词： 覆冰四分裂导线     动态气动力系数     舞动     数值模拟    
Dynamic aerodynamic characteristics of iced quad bundled conductors
YANG Xiuping1,2, ZHANG Zhe2, HAO Shuying2     
1. Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System, Tianjin University of Technology, Tianjin 300384, China;
 2. School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384, China
Abstract: In order to study the aerodynamic characteristics of galloping of iced bundle conductors, based on software Fluent, the program described the track of conductor galloping by user-defined function and dynamic mesh technology are used to realize the fluid-solid coupling. The dynamic aerodynamic coefficients of crescent iced quad bundle conductors in the lateral vibration are calculated and compared with the results from simulation in static; the effects of galloping amplitude and frequency on the dynamic aerodynamic forces are analyzed. The results show that the dynamic aerodynamic coefficients are larger than that of statics; and they have the same variation laws under the same wind speed. The influence of the wake of windward sub-conductors on the leeward sub-conductors reduces because of wake excursion, dynamic aerodynamic coefficients of leeward sub-conductors are larger evidently than that of statics. Drag and lift coefficients increase with the galloping amplitude and frequency increasing: but the effect of frequency on the dynamic aerodynamic force is less than that of amplitude. The effects of dynamic aerodynamic coefficients on galloping should not be ignored to forecast the critical wind speed of conductor break and tower loads caused by large span galloping in engineering.
Key words: iced quad bundle conductors     dynamic aerodynamic coefficient     galloping     numerical simulation    

导线覆冰之后形成非对称面，在自然风作用下易发生低频大振幅的舞动，造成断线倒塔等事故，对输电线路的安全构成严重威胁.国内外研究资料表明，在相同的条件和气象环境下，四分裂导线比单导线更容易发生舞动[1].覆冰导线的气动力特性是诱发舞动的重要因素，因此研究覆冰四分裂导线气动力特性对舞动防止技术的研究具有重要意义.

目前，国内外在研究覆冰导线舞动行为时，一般将静态试验中获得的气动力系数用于动态舞动的计算研究[2-4].由于导线舞动时，其气动力随导线位置、速度等因素时刻变化，这种“准静态”假设并不完全适用，对于分裂导线，迎风侧子导线动态时尾流对背风侧子导线的影响与静态时也不相同，因此研究覆冰导线舞动时，有必要采用动态试验和模拟的方法来考察动态气动力系数，以便进一步准确预测和抑制舞动.

国内李万平[5]对三分裂覆冰导线进行了动态气动力特性试验，讨论了准静态假设在覆冰导线群的驰振分析中的适用性，但试验仅考虑了导线的扭转振动，而忽略了易引起断线等事故的横向振动.国外Kimura等[6]和Shimizu等[7]对类似新月形覆冰导线在横向振动和扭振状态下的升力和扭转系数进行试验研究，比较了动态气动力与静态气动力的不同.Braun等[8]使用Newmark-β方法求解动力平衡方程，建立流固耦合模型分析了分裂导线的绕流场.目前，对于覆冰多分裂导线的动态气动力特性的实验和仿真计算的研究未见报道.

由于动态气动力系数的获得需要更为复杂的试验设备和装置，特别是大档距时，舞动振幅较大，需要更大的试验空间和巨大的成本.采用数值方法，基于流体动力学仿真软件Fluent，利用用户自定义函数UDF对四分裂导线的舞动轨迹进行编程并结合动网格技术实现流固耦合，研究覆冰导线横向振动时气动力系数的变化规律，分析舞动振幅和频率对气动力的影响.

1 基本理论与方法

流体域的控制方程可用二维不可压缩粘性流体的连续性方程和N-S方程来描述.

连续方程

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$    (1)

动量方程

$\left\{ \begin{align} & \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{\mu }{\rho }(\frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{y}^{2}}})-\frac{1}{\rho }\frac{\partial p}{\partial x} \\ & \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=\frac{\mu }{\rho }(\frac{{{\partial }^{2}}v}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}v}{\partial {{y}^{2}}})-\frac{1}{\rho }\frac{\partial p}{\partial y} \\ \end{align} \right.$    (2)

式中：ρ为流体密度，kg/m3；μ为动力粘度系数，Pa·s；p为流体压强，Pa；u、v分别为流体沿x方向和y方向的速度，m/s.

湍流模型采用标准k-ε模型，输运方程为

$\left\{ \begin{align} & \frac{\partial (\rho \text{k)}}{\partial t}+\frac{\partial (\rho k{{u}_{i}})}{\partial {{x}_{i}}}= \\ & \frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu \text{+}\frac{{{\mu }_{\text{i}}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+{{G}_{k}}-\rho \varepsilon \\ & \frac{\partial (\rho \varepsilon \text{)}}{\partial t}+\frac{\partial (\rho \varepsilon {{u}_{i}})}{\partial {{x}_{i}}}= \\ & \frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu \text{+}\frac{{{\mu }_{\text{i}}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+\frac{\varepsilon }{k}({{C}_{1\varepsilon }}{{G}_{k}}-{{C}_{2\varepsilon }}\rho \varepsilon ) \\ \end{align} \right.$    (3)

式中：σk和σε分别为湍动能k和耗散率ε对应的Prandtl数；μi为湍流粘性系数，μi=ρCμk2/ε;C1ε、C2ε和Cμ为经验常数.

覆冰导线所受空气动力载荷主要为阻力FD、升力FL和扭矩FM，分别表示为

$\begin{align} & {{F}_{D}}=\rho {{U}^{2}}LD{{C}_{d}}/2 \\ & {{F}_{L}}=\rho {{U}^{2}}LD{{C}_{l}}/2 \\ & {{F}_{M}}=\rho {{U}^{2}}L{{D}^{2}}{{C}_{m}}/2 \\ \end{align}$    (4)

式中：CD、CL和CM分别为阻力、升力和扭矩系数；U为风速，m/s；L为导线长度，m；D为导线直径，m.

实验和数值模拟[1, 6-9]表明，覆冰导线舞动轨迹为斜椭圆，其运动参数化方程可表示为

$\left\{ \begin{matrix} x(t)=b\cos \beta \cos (\omega t-\beta )-a\sin \beta \sin (\omega t-\beta ) \\ y(t)=b\sin \beta \cos (\omega t-\beta )+a\cos \beta \sin (\omega t-\beta ) \\ \end{matrix} \right.$    (5)

运动速度为

$\left\{ \begin{matrix} \dot{x}(t)=-\omega b\cos \beta \sin (\omega t-\beta )-\omega a\sin \beta \cos (\omega t-\beta ) \\ \dot{y}(t)=-\omega b\sin \beta \sin (\omega t-\beta )+\omega a\cos \beta \cos (\omega t-\beta ) \\ \end{matrix} \right.$    (6)

式中:ω为导线舞动的圆频率，s-1；a为椭圆轨迹的半长轴，m；b为椭圆轨迹的半短轴，m；β为椭圆长轴与y轴正方向的夹角.

2 静、动态气动力特性比较 2.1 计算模型

以新月形覆冰四分裂导线为研究对象，根据文献[9]中的风洞试验模型，选取导线直径D为27.6 mm，覆冰厚度H为12 mm，子导线间距A为450 mm，如图 1(a)所示，风速为14 m/s，分别计算了不同攻角下静、动态气动力系数.

建立计算模型时，为使尾流能充分发展，减小边界对流场计算的影响，计算域根据阻塞率不大于3%[10]，取为-68D≤x≤83D，-54D≤y≤54D，坐标原点为初始时刻子导线1的中心，4根子导线运动方式相同，且保持相同的风攻角；采用分块非结构化网格，总网格数约为14万，计算步长为0.004 s.

动态模拟时，覆冰导线运动区域定义为动网格，该部分网格随覆冰导线截面的运动而变化，用弹簧光顺法和尺度函数修改网格形状及尺度，在覆冰导线所在的中心及动网格区域局部加密，图 1(b)为动态计算区域示意图.根据式(5)、(6)利用VC++编写用户自定义函数控制导线舞动的轨迹及速度，导线舞动的振幅和频率根据文献[9]选取，档距为100 m时，a=830 mm，b=346 mm，β=30°，频率f=0.5 Hz，导线按逆时针方向舞动.

图 1 模型计算及区域示意图 Figure 1 Schematic diagram of model and calculation area
图选项

静、动态模拟边界条件相同，入口为速度入口，出口为压力出口，上、下两侧采用对称边界条件，覆冰导线的表面为壁面.

2.2 气动力系数

文献[9]风洞实验测量静态气动力系数时，来流方向和边界条件不变，将4根子导线模型固定在2个平行的圆盘之间，改变攻角时转动圆盘，4根子导线随之共同转动.这样，导线攻角改变的同时，4根子导线之间的迎风面和背风面的顺序、分布方式及导线间距均发生改变，显然与导线实际工况不符.实验测得的气动力系数不能完全准确地反映尾流影响及实际静态气动力特性[11, 12].数值模拟时，每10°攻角建立1个四分裂导线模型，来流方向始终为水平方向，边界条件保持不变.

图 2为静、动态气动力系数的比较曲线，2种气动力系数随攻角的变化规律相同.迎风侧子导线的尾流对背风侧子导线周围流场的影响，使背风侧子导线受到的气动力减小，尤其是阻力和扭转系数.攻角为0°和180°时，子导线1和2迎风的截面积最小，阻力系数最小，90°攻角时，子导线1和2迎风的截面积最大，阻力系数最大，这时尾流效应最明显.

图 2 静、动态气动力系数的比较曲线 Figure 2 Comparison with the aerodynamic coefficients of statics and dynamics
图选项

对于迎风侧子导线1和2，其动态气动力系数略大于静态值，而背风侧子导线3和4的动态阻力系数比静态大0.1~0.21，动态升力系数比静态值最大相差0.48，动态扭转系数比静态值最大相差0.14.显然，动态时迎风侧和背风侧的气动力系数的差别减小，90°攻角处迎风侧子导线的阻力系数比背风侧大0.65(静态时为0.78)；40°攻角处，扭转系数大0.2(静态时为0.35).

图 3、4分别为60°攻角时迎风侧和背风侧子导线静、动态阻力系数和升力系数随时间变化曲线及对应的频谱，由于导线舞动时扭转中心随时间变化，计算时每个舞动周期选取10个位置，随时更新扭转中心坐标，记录和读取相应的扭矩系数，然后取平均值，因此文中未给出动态扭矩系数随时间变化曲线.

图 3 迎风侧子导线的阻力、升力系数曲线及频谱 Figure 3 Time history curves and spectrums of drag and lift coefficients for windward sub-conductors
图选项

由图 3可以看出，迎风侧子导线动态气动力系数平均值略大于静态值，阻力系数振动的主频为0.5 Hz，与舞动频率相同；升力系数振动有多个频率成分.由图 4可知，背风侧子导线动态气动力系数平均值明显大于静态值，受迎风侧子导线尾流的影响，阻力系数振动有2个频率，分别为0.5、1 Hz，升力系数振动比迎风侧子导线更复杂，没有明显的主频.

图 4 背风侧子导线阻力、升力系数曲线及频谱 Figure 4 Time history curves and spectrums of drag and lift coefficients for leeward sub-conductors
图选项
2.3 结果分析

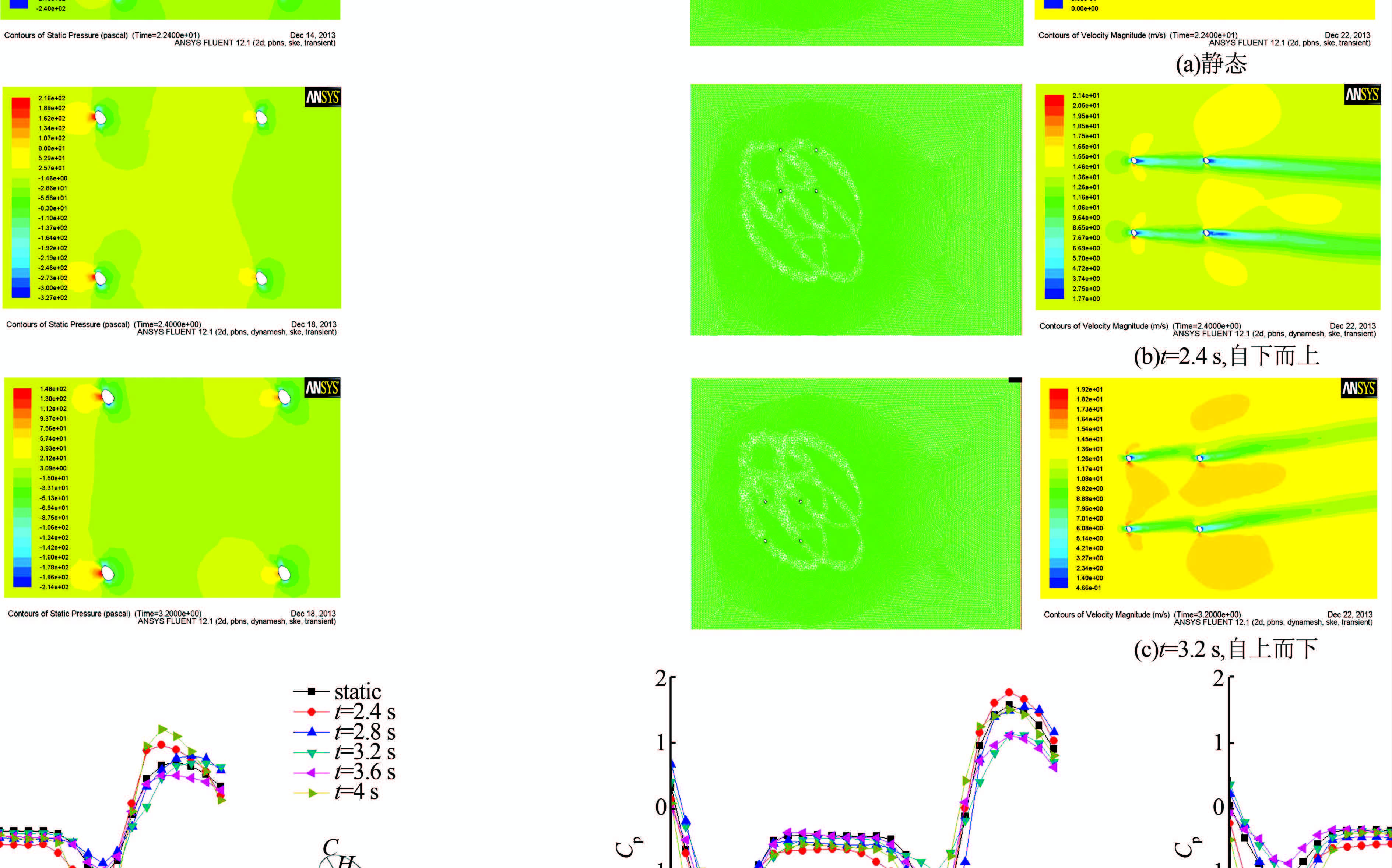
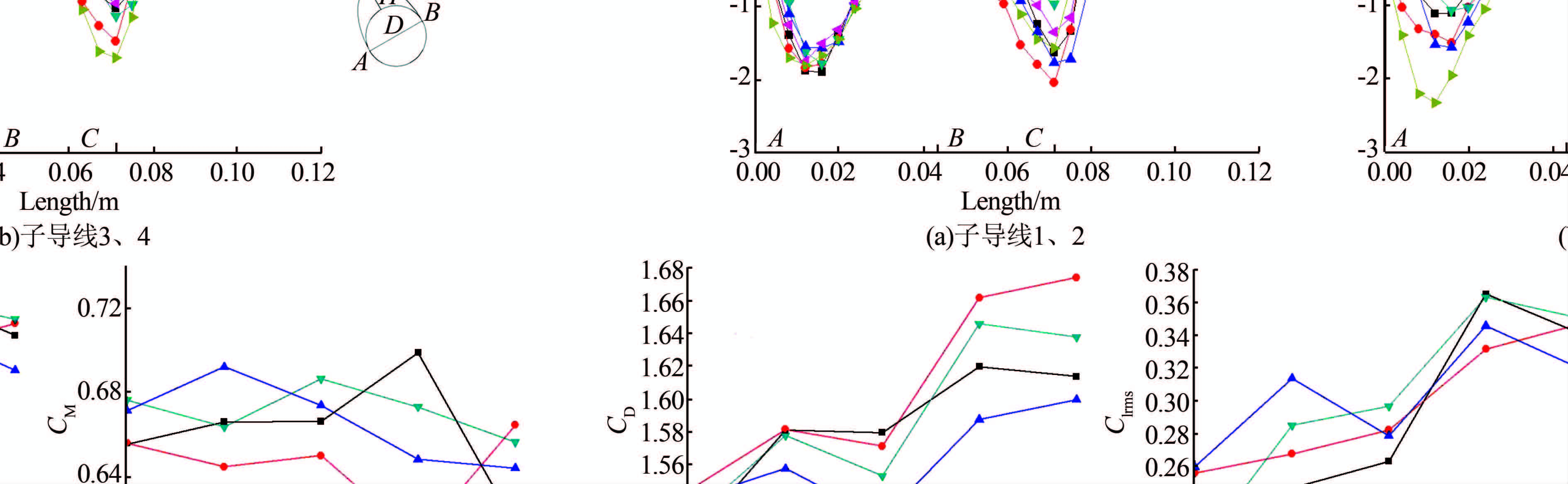
分裂导线动态气动力与运动时导线的位置和速度有关，以攻角60°为例进行分析，静态及动态四分裂导线1个周期内不同位置时网格、速度与压力分布(篇幅限制，仅给出2个位置)如图 5所示.图 6为压力系数分布曲线，横坐标起点A从图中导线的A点位置开始，按逆时针方向沿导线表面周向长度计算，B、C点的位置也与导线上的位置相对应.

图 5 静、动态网格、速度与压力云图 Figure 5 Distributions of mesh,velocity and pressure in static and dynamic simulation
图选项
图 6 压力系数分布的比较 Figure 6 Comparison with pressure coefficients distribution
图选项

与静态时相比(图 5(a)及图 6中的static曲线)，导线自下向上运动时(对应图 5(b)和图 6中t=2.4、4 s的曲线)，水平振动速度方向与来流速度方向相反，合成后使速度减小，驻点压力增加，分离点向覆冰一侧前移，背风面压力降低，阻力增加；垂直方向振动使顶部速度增加，负压增大，底部负压减小，使升力增大.

导线自上向下时(对应图 5(c)和图 6中t=2.8、3.2 s的曲线)，水平振动速度方向与来流速度方向一致，合成后使速度增大，驻点压力减小，且位置下移，底部分离点后移，但覆冰侧的分离点基本没变，背风面负压区的压力仍比静态时小，因此阻力变化不明显；垂直方向振动使底部速度增加，压力减小，由于底部形状为圆弧，底部负压区域减小，顶部负压区域增大，升力略有增加.

综合整个周期，导线的动态气动力系数的平均值均大于静态值.由于导线舞动时，迎风侧子导线尾流的偏移，使背风侧的子导线受到迎风侧尾流的压力和速度的影响减小，故背风侧子导线的动态气动力系数比静态时显著增加.

3 舞动幅值和频率的影响

覆冰导线舞动是一种低频、大振幅的自激振动，其振动频率通常为0.1～3 Hz，振幅约为导线直径的5～300倍[1].为研究舞动幅值和频率对气动力的影响，模拟中选取振幅为0.06~1.66 m，椭圆长轴与短轴的比为2.4，舞动频率分别为0.5、0.83 Hz，不考虑扭转振动的影响.其他参数与2.1节计算模型相同.

图 7为气动力系数随舞动幅值和频率变化的关系曲线，可以看出，4根子导线阻力系数的平均值和升力系数的均方根值都随振幅和频率的增加而增大，迎风侧子导线和背风侧子导线的变化趋势相近.扭转系数受到子导线间阻力、升力和钝体之间更加复杂的尾流干扰等因素的影响，其变化没有明显规律.对于子导线3在0.83 Hz下，振幅从0.06 m增至1.66 m时，阻力系数增加了0.27(29%)，升力系数增加了0.13(76%)；子导线3在1.66 m振幅下，0.83 Hz比0.5 Hz的阻力系数增加了0.18(18%)，升力系数增加了0.05(21%).显然振幅对动态气动力系数的影响更明显.

图 7 舞动的幅值和频率对动态气动力系数的影响 Figure 7 Galloping amplitude and frequency effects on dynamic aerodynamic coefficients
图选项

设计输电线路及防舞研究时，通常不考虑档距和舞动幅值的影响，假设都具有相同的静态气动系数.由于导线舞动幅值随线路档距的增大而增加，动态气动系数相应增大，所以对于大档距线路，采用动态气动系数计算的导线实际舞动的幅值大于依照静态气动系数计算得到的幅值，导线实际承受的动态张力及其作用在输电塔上的力远大于由静态计算给出的结果.同时输电线张力的增加改变了输电线的刚度，刚度的增加使得系统的瞬时固有频率增大[13]，阻力系数和升力系数随频率的增大而增加，这也将使气动力增加.因此预测导线舞动引起的断线的临界风速和塔承受的荷载时，特别是大档距，应考虑动态气动力系数对舞动的影响.

4 结论

1) 四分裂覆冰导线横向振动时的动态气动力系数均大于静态值，其变化规律基本相同.

2) 导线舞动时，迎风侧子导线尾流偏移，其压力和速度对背风侧子导线的影响减小，背风侧子导线的动态气动力系数比静态时明显增加.

3) 相同攻角和风速下，阻力、升力系数随舞动幅值和频率的增加而增大，但频率对动态气动力的影响小于幅值的影响.

4) 工程中预测大档距导线舞动引起的断线的临界风速和塔承受的荷载时，应考虑动态气动力系数对舞动的影响.

参考文献
[1] 郭应龙, 李国兴, 龙传永. 输电线路舞动[M]. 北京: 中国电力出版社, 2003.
Guo Yinglong, Li Guoxing, Long Chuanyong. Transmission Line Dancing[M]. Beijing: China Electric Power Press, 2003.
[2] 王昕, 楼文娟, 沈国辉, 等. 覆冰导线气动力特性风洞试验研究[J]. 空气动力学报, 2011, 29(5): 573–579.
Wang Xin, Lou Wenjuan, Shen Guohui, et al. A wind tunnel study on aerodynamic characteristics of iced conductor[J]. Acta Aerodynamica sinica, 2011, 29(5): 573–579.
[3] 张宏雁, 严波, 刘小会, 等. 覆冰导线气动特性及驰振风洞试验[J]. 振动与冲击, 2013, 32(10): 95–99.
Zhang Hongyan, Yan Bo, Liu Xiaohui, et al. Wind-tunnel tests for aerodynamic characteristics and galloping behaviors of iced conductors[J]. Journal of Vibration and Shock, 2013, 32(10): 95–99.
[4] 王侠. 覆冰导线空气动力特性风洞试验及数值模拟[D]. 重庆:重庆大学, 2012.
Wang Xia. Numerical simulation and wind tunnel tests of aerodynamic forces of iced conductors[D]. Chongqing: Chongqing University, 2012.
[5] 李万平. 覆冰导线群的动态气动力特性[J]. 空力动力学报, 2000, 18(4): 413–420.
Li Wanping. Dynamic aerodynamic characteristics of the galloping of bundled iced power transmission lines[J]. Acta Aerodynamica SINCA, 2000, 18(4): 413–420.
[6] Kimura K M, Inoue Y, Fujino T, et al. Unsteady forces on an ice-accreted four-conductor bundle transmission line[C]// Proceedings of the 10th Int. Conference on Wind Engineering, Copenhagen:Denmark, 1999: 467-472.
[7] Shimizu M, Ishihara T, Phuc P V. A wind tunnel study on steady and unsteady aerodynamic characteristics of ice-accreted transmission lines[C]// Proceedings of the 18th Symposium on Wind Engineering, Tokyo, Japan, 2004: 245-250.
[8] Braun A L, Awruch A M. Aerodynamic and aeroelastic analysis of bundled cables by numerical simulation[J]. Journal of Sound and Vibration, 2005, 284(1-2): 51–73. DOI:10.1016/j.jsv.2004.06.026
[9] 严波, 胡景, 周松, 等. 覆冰四分裂导线舞动数值模拟及参数分析[J]. 振动工程学报, 2010, 23(3): 310–316.
Yan Bo, Hu Jing, Zhou Song, et al. Numerical simulation and parameter analysis of galloping for iced quad-bundled conductor[J]. Journal of Vibration Engineering, 2010, 23(3): 310–316.
[10] 孙晓颖,许伟,武岳. 钝体绕流中的计算域设置研究[C]//第十三届全国结构风工程学术会议论文集. 大连:大连理工大学出版社,2007:1036-1041.
Sun Xiaoying, Xu Wei, Wu Yue. Research on calculation domain of flow around blunt bodies[C]//Proceedings of the 13th National Conference on Structural Wind Engineering. Dalian: Dalian University of Technology Press, 2007:1036-1041.
[11] 蔡萌琦, 严波, 吕欣, 等. 覆冰四分裂导线空气动力系数数值模拟[J]. 振动与冲击, 2013, 32(5): 132–137.
Cai Mengqi, Yan Bo, Lv Xin, et al. Numerical investigation on aerodynamic coefficients of iced quad bundle conductor[J]. Journal of Vibration and Shock, 2013, 32(5): 132–137.
[12] 吕翼, 楼文娟, 孙珍茂, 等. 覆冰三分裂导线气动力特性的数值模拟[J]. 浙江大学学报(工学版), 2011, 44(1): 174–179.
Lv Yi, Lou Wenjuan, Sun Maozhen, et al. Numerical simulation of aerodynamic characteristics of three bundled iced transmission lines[J]. Journal of Zhejiang University (Engineering Science), 2011, 44(1): 174–179.
[13] 郝淑英, 冯海茂, 范孜, 等. 覆冰输电线非线性瞬时固有频率研究[J]. 工程力学, 2013, 30(9): 283–287.
Hao Shuying, Feng Haimao, Fan Zi, et al. Investigation of nanlinear transient natural frequency of iced transmission line[J]. Engineering Mechanics, 2013, 30(9): 283–287.