武汉大学学报(工学版)   2016, Vol. 49 Issue (2): 236-241

文章信息

孙志达, 陈红坤, 胡畔, 邓云飞, 曾爽
SUN Zhida, CHEN Hongkun, HU Pan, DENG Yunfei, ZENG Shuang
基于实测数据的电气化铁路冲击负荷建模
Electrified railway impact load modeling based on measured data
武汉大学学报(工学版), 2016, 49(2): 236-241
Engineering Journal of Wuhan University, 2016, 49(2): 236-241
http://dx.doi.org/10.14188/j.1671-8844.2016-02-013

文章历史

收稿日期: 2014-10-20
 Abstract              PDF               Figures               Tables
引用本文 0
孙志达, 陈红坤, 胡畔, 邓云飞, 曾爽. 基于实测数据的电气化铁路冲击负荷建模[J]. 武汉大学学报(工学版), 2016, 49(2): 236-241.
SUN Zhida, CHEN Hongkun, HU Pan, DENG Yunfei, ZENG Shuang. Electrified railway impact load modeling based on measured data[J]. Engineering Journal of Wuhan University, 2016, 49(2): 236-241.
基于实测数据的电气化铁路冲击负荷建模
孙志达, 陈红坤, 胡畔, 邓云飞, 曾爽     
1. 武汉大学电气工程学院，湖北 武汉 430072;
 2. 国网北京市电力公司，北京 100075
收稿日期: 2014-10-20
作者简介: 孙志达(1991-)，男，硕士研究生，研究方向为电力系统运行与控制，E-maill：sunpalstar@163.com.
通讯作者: 陈红坤(1967-)，男，博士，教授，博士生导师，研究方向为电力系统运行与控制，E-mail：chkinsz@163.com
摘要: 基于电力系统负荷建模基础理论和电气化铁路系统结构，建立一种电气化铁路冲击负荷模型.对实测电气化铁路冲击负荷的负荷曲线进行小波分析法去噪并用作模型参数辨识.面向电网PCC点建立交直型和交直交型电力机车的综合负荷特性模型，形成电气化铁路冲击负荷模型结构.制定模型参数辨识策略并加以实施.针对冲击负荷的主动性特点对模型进行改进，并将其与原模型进行比较分析.通过算例分析验证了该建模方法的可行性.
关键词： 实测数据     电气化铁路     冲击负荷     建模     参数辨识    
Electrified railway impact load modeling based on measured data
SUN Zhida, CHEN Hongkun, HU Pan, DENG Yunfei, ZENG Shuang     
1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;
 2. State Grid Beijing Electric Power Company, Beijing 100075, China
Abstract: An electrified railway system impact load model is built based on the basic theory of power system load modeling and electrified railway system structure. Denoise measured electrified railway impact load curve by wavelet analysis method and is used as a model parameter identification. Oriented to the point of common coupling (PCC), the AC-DC and AC-DC-AC integrated electric locomotive model is established, forming an electrified railway impact load model structure. The model parameter identification strategies are developed and implementing them. And the model is improved for the initiative characteristics of impact load and carrying out comparative analysis with the original model. The feasibility of this modeling method is verified by a case study.
Key words: measured data     electrified railway     impact load     modeling     parameter identification    

电气化铁路(电铁)牵引负荷由于存在特殊性和复杂性，使用现场分析和事故再现的方法不具备可行性.随着计算机技术的发展，通过采用计算机仿真技术模拟电铁系统的运行过程，进而对牵引供电系统进行研究的方法逐渐被人们所采纳[1].该方法基于实际牵引供电系统的机理，通过在Matlab、PSS/E、PSCAD等仿真软件中搭建模型来模拟各种运行工况下的牵引负荷，从而研究其相关特性.文献[1-2]在建立物理机理模型的基础上，建立了反映牵引供电系统负荷特性的数学模型；文献[3-4]基于电力机车原理，完成电力机车在不同工况下的仿真，并且对仿真波形与实测波形进行比较；文献[5-6]侧重分析了牵引负荷谐波的情况.文献[7-8]通过分析交-直变换元件的控制策略，提出了谐波电流概率模型；文献[9]认为牵引供电系统的电压由机车速度和系统最大功率吸收这两个随机因素决定，进而提出了一种牵引供电系统的概率模型.

目前电铁负荷建模研究存在以下三点不足：第一，目前研究中所建立的随机过程模型多为非机理模型，该模型对于电铁牵引负荷而言缺乏明确的物理意义.此类负荷模型的针对性不强；第二，现有仿真研究主要集中在电力机车本身机理描述，进而研究其电能质量特性或者其作为常规负荷的负荷特性.此类模型无法考虑牵引负荷在运行中的由主动功率需求所表现出来的冲击特性对电网的影响.第三，现有模型还无法全面模拟牵引供电负荷在各种工况下的特性，适应性方面有待提高.

综上所述，目前国内外在电力系统冲击负荷建模领域尚未形成系统的建模理论，可用于实际电力系统的电铁冲击负荷模型极少.面对电气化铁路负荷接入数量和接入容量剧增的现状，对电铁冲击负荷进行建模研究刻不容缓.

1 电铁冲击负荷实测数据预处理

为充分体现电铁负荷的冲击特性，结合实际测量条件，选取某一向牵引站供电的变电站母线为测量点，以在该母线处测量的一组典型而且完整的冲击特性曲线作为分析对象，如图 1所示：

图 1 电压、电流、视在功率实测曲线 Figure 1 Measured curve of voltage,current and apparent power
图选项

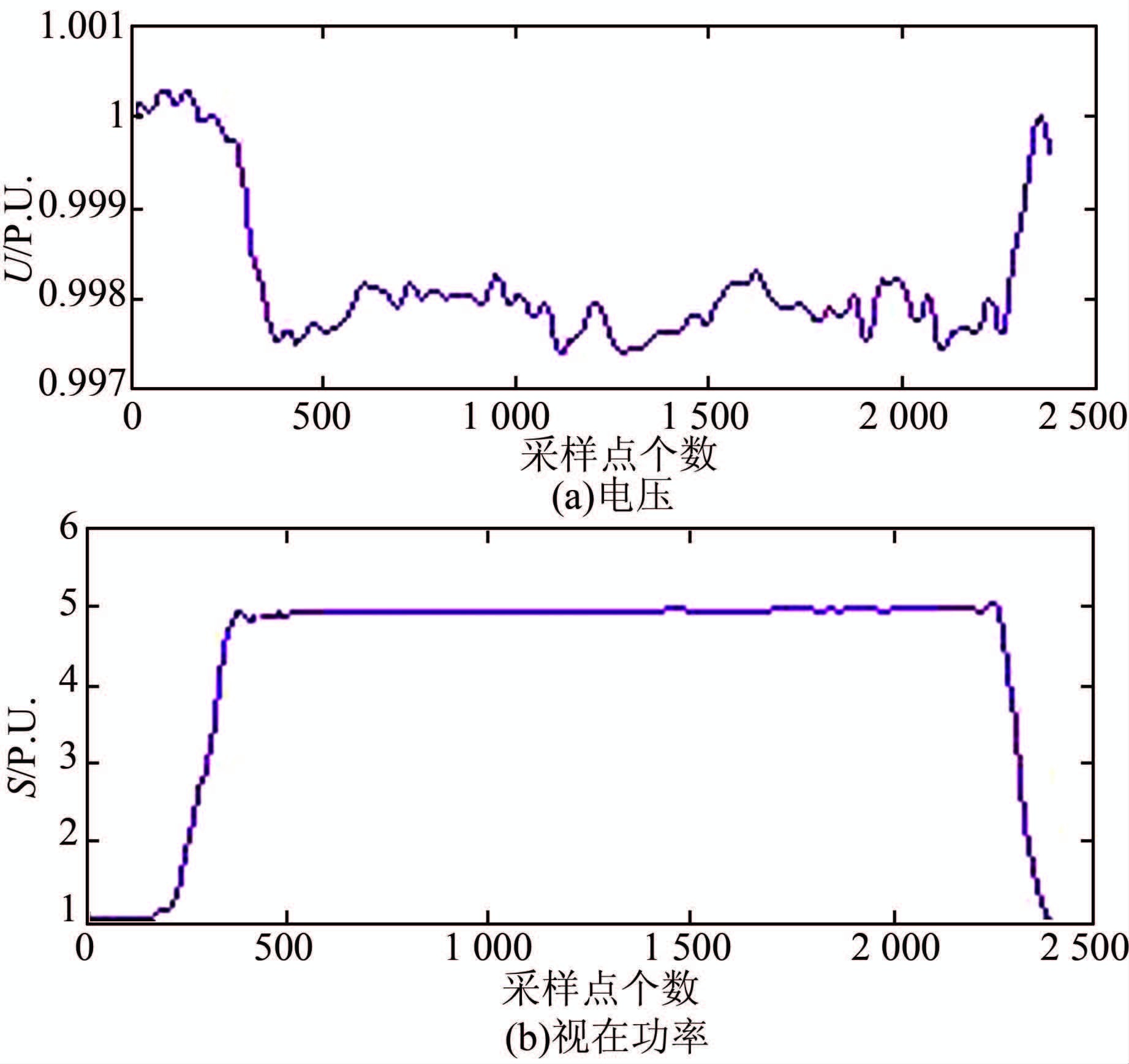
采用小波分析技术对实测数据进行滤波.根据多次实践结果比对，采用db5小波对实测数据进行5层分解，并进行去噪.本文将去噪之后的电压信号取作模型电压输入.对于功率实测数据作同样处理，可以得到如图 2所示曲线.

图 2 去噪后的电铁冲击负荷曲线 Figure 2 The curve of electrified railway impact load after denoising
图选项

将小波变换分解并去噪之后的信号用作模型参数辨识和模型验证.至此，完成了实测数据的预处理工作.

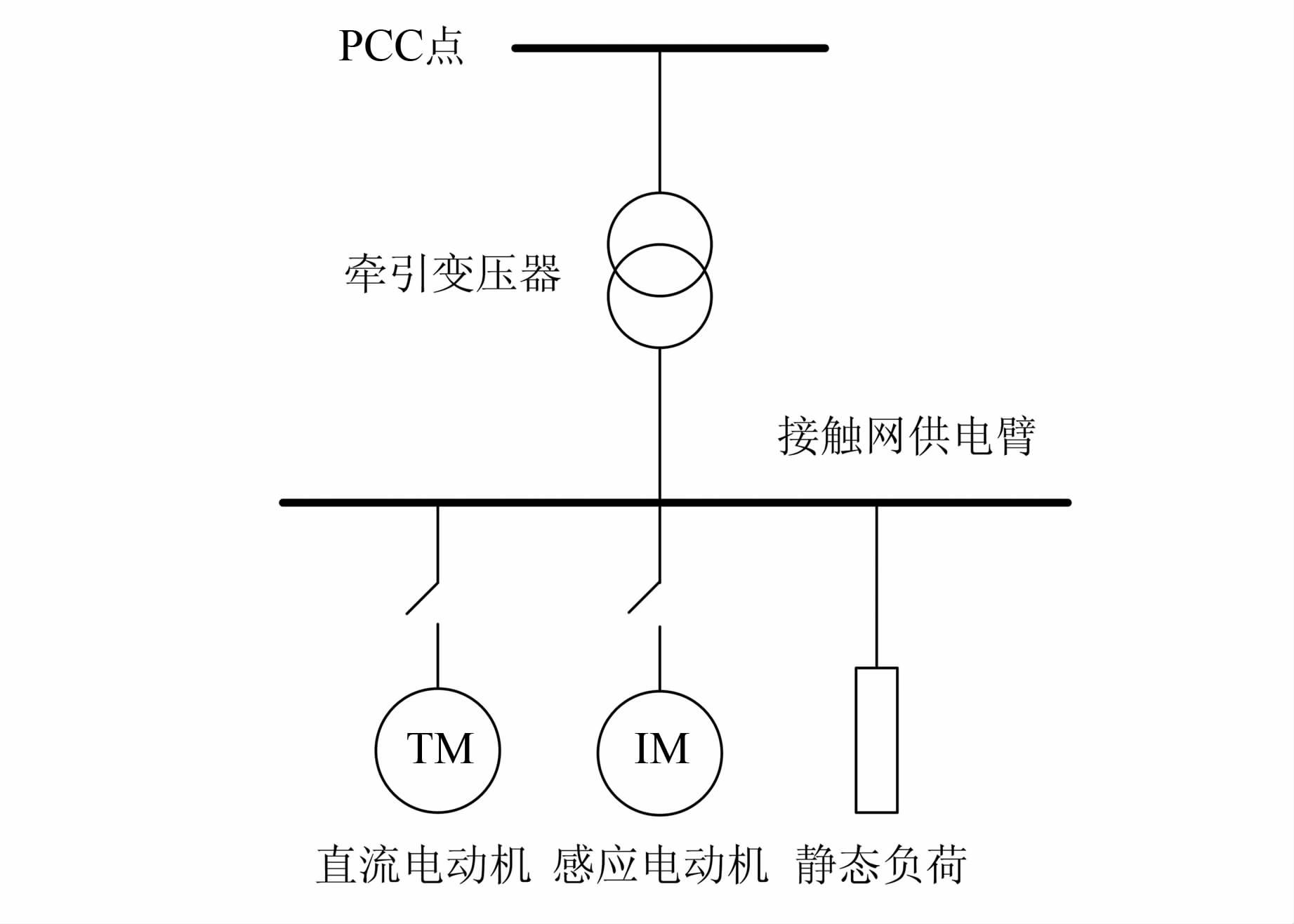
2 电铁冲击负荷模型结构

电力机车模型的建立是面向为牵引站供电的变电站PCC点，并且模型将输电线路和牵引供电系统综合考虑进去，可以用来描述电气化铁路牵引供电系统及电力机车负荷随系统电压变化的特性.铁路系统电力机车种类繁多，不同的线路上电力机车的类型不尽相同.例如，武广线为高速铁路客运专线，合武线为动车客运专线，京九线为南北干线客货混运既有铁路.因此，有必要将电力机车模型进行整合，形成具备多样化描述能力的电铁负荷特性模型.进行整合之后的负荷模型由直流电动机、感应电动机和静态负荷组成，如图 3所示.

图 3 电气化铁路牵引负荷 Figure 3 Electrical railway traction load
图选项

将系统三相侧电压作为激励的直流电动机电路状态方程[10]：

$\left\{ \begin{align} & \frac{d{{I}_{d}}}{dt}=\frac{1}{L}(\frac{U}{{{K}_{zu}}}-{{I}_{d}}R-{{C}_{1}}{{I}_{d}}\omega ) \\ & \frac{d\omega }{dt}=\frac{1}{J}({{C}_{1}}{{I}_{d}}^{2}-(A{{\omega }^{2}}+B\omega +C){{T}_{L0}}) \\ \end{align} \right.$    (1)

式中：Id为直流电动机端口电流；ω为直流电动机角速度；L为电路等值电感；U为母线PCC点母线电压；Kzu为压变换系数；R为等值电阻；C1=CTKs；CT为转矩常数，Ks为牵引电机励磁系数；J为转动惯量；(Aω2+Bω+C)TL0=TL，TL为直流电动机的机械负载转矩，其中，Aω02+Bω0+C=1，ω0为电机初始稳态角速度，TL0为初始稳态机械转矩.

因此，基于牵引电动机电路电压方程可推得牵引电动机吸收的有功功率Pz：

${{P}_{z}}={{U}_{d}}\cdot {{I}_{d}}$    (2)

牵引电动机电路吸收的无功功率主要受电力机车牵引电动机电路中的机车主变压器、直流电动机励磁、整流电路等方面的影响.它的大小与电力机车的运行状态密切相关.考虑到机车的功率因素随着接触网的电压变化呈极为复杂的非线性关系，根据输入/输出模型建模思想和机车模型的整体描述能力，将其整合至静态负荷无功功率部分描述.

采用以极坐标形式表示的感应电动机模型方程为

$\left\{ \begin{align} & {T}'\frac{d{E}'}{dt}=-{E}'+C{{U}_{u}}\cos \delta \\ & \frac{d\delta }{dt}=\omega -{{\omega }_{v}}-\frac{C{{U}_{u}}}{{T}'{E}'}\sin \delta \\ & {{T}_{j}}\frac{d\omega }{dt}=-\frac{{{U}_{u}}{E}'}{{{X}'}}\sin \delta -{{T}_{M}} \\ \end{align} \right.$    (3)

吸收的功率为

$\left\{ \begin{align} & {{P}_{j}}=-\frac{{{U}_{u}}{E}'}{{{X}'}}\sin \delta \\ & {{Q}_{j}}=\frac{{{U}_{u}}({{U}_{u}}-{E}'\cos \delta )}{{{X}'}} \\ \end{align} \right.$    (4)
${{U}_{u}}=U/{{K}_{ju}}$    (5)

其中:C=(X-X′)/X；T′=(X′/X)/Td0′；E′为暂态电抗后电动势；X′为暂态电抗；X为同步电抗；Td0′为暂态时间常数；Tj为惯性时间常数；TM=TM0ωN，为机械转矩[11]；ω和ωv分别为转子转速和同步转速；δ为功角；U为PCC点母线电压；Uu为感应电动机机端电压；Kju为电压变换系数.

为减少辨识参数，提高对模型主要参数的辨识效率和精度，静态负荷模型采用下式所示的幂函数形式表示.由于静态负荷部分为电压比值形式，故可不考虑其电压变比关系.另外，由于模型是面向PCC点，静态负荷部分包含了对供电线路功率损耗的考虑.该幂函数形式为

$\left\{ \begin{align} & {{P}_{s}}(t)={{P}_{s}}_{0}{{(\frac{U}{{{U}_{0}}})}^{{{P}_{u}}}} \\ & {{Q}_{s}}(t)={{Q}_{s}}_{0}{{(\frac{U}{{{U}_{0}}})}^{{{Q}_{u}}}} \\ \end{align} \right.$    (6)

其中：Pu、Qu反映了负荷的静态特性，是负荷模型参数辨识的对象；U0、Ps0、Qs0由稳态运行条件确定.为提高模型的自适应性，引入直流牵引电动机初始有功和无功功率比例系数Kzp、Kzq，则有：

$\left\{ \begin{align} & {{P}_{s}}_{0}=(1-{{K}_{zp}}){{P}_{0}} \\ & {{Q}_{s}}_{0}=(1-{{K}_{zq}}){{Q}_{0}} \\ \end{align} \right.$    (7)

其中:P0、Q0为模型初始总有功和无功功率，Kzq=0.

定义感应电动机负荷和直流电动机负荷的开关系数分别为K1和K2，其中K1、K2取值0或1，K1和K2不同时为0.得到如下模型结构：

$\left\{ \begin{align} & {{P}_{l}}={{K}_{1}}{{P}_{j}}+{{K}_{2}}{{P}_{z}}+{{P}_{s}} \\ & {{Q}_{l}}={{K}_{1}}{{Q}_{j}}+{{Q}_{s}} \\ \end{align} \right.$    (8)

1) 当K1=0，K2=1时，为交直型电力机车负荷模型；

2) 当K1=1，K2=0时，为交直交型电力机车负荷模型；

3) 当K1=1，K2=1时，为交直型和交直交型机车混合负荷模型.

式(8)中：Pl、Ql为总有功和无功功率；Pj、Qj为感应电动机吸收的有功和无功功率；Pz为直流电动机吸收的有功功率；Ps、Qs为静态负荷吸收的有功和无功功率.

基于输入/输出式模型的建模思想，本文提出采用式(8)描述电铁负荷的冲击特性：

$\left\{ \begin{align} & {{P}_{i}}={{e}^{(U-{{U}_{0}}){{K}_{p}}}}-1 \\ & {{Q}_{i}}={{e}^{(U-{{U}_{0}}){{K}_{q}}}}-1 \\ \end{align} \right.$    (9)

其中：U0为稳态电压；Kp、Kq分别为有功和无功冲击功率随电压的变化系数.利用式(8)与(9)综合得到式(10)所示电铁冲击负荷综合模型结构：

$\left\{ \begin{align} & P={{K}_{1}}{{P}_{j}}+{{K}_{2}}{{P}_{z}}+{{P}_{s}}\text{+}{{P}_{i}} \\ & Q={{K}_{1}}{{Q}_{j}}+{{Q}_{s}}+{{Q}_{i}} \\ \end{align} \right.$    (10)

综上所述，考虑到模型的可辨识性[12]，根据参数灵敏度分析结果，选取以下参数作为电铁冲击负荷模型独立待辨识参数：

$[L,J,R,{{C}_{1}},{{K}_{zp}},C,{T}',{X}',N,{{K}_{jp}},{{K}_{p}},{{K}_{q}}]$
3 模型的参数辨识 3.1 辨识策略的选取

系统辨识是根据输入和输出数据选择一个与实际系统等价的系统.因此，在具体系统辨识实践时，首先需要基于输入输出信息，选定一类系统进行参数辨识，然后评价此系统与实际系统是否等价.

本文选取粒子群优化算法(PSO)[13-15]作为模型辨识基本算法.与非随机类方法相比，PSO算法应用于电力负荷参数辨识具有全局性好、鲁棒性强、精度高等特点；与随机类方法中的遗传算法(GA)相比，PSO算法收敛速度更快，而且可以在同等时间内以更高的全局最优概率求解负荷参数；算法实现简单，不需要编码，没有交叉和变异操作，只是通过粒子速度和位置进行更新寻优.因此，原理更简单，参数更少，更易实现.

本文所建模型待辨识参数个数相对较多，为了提高辨识精确度和寻优效率，PSO算法为最佳选择.

模型中其他参数选取典型值[11-12]如表 1所示.

表 1 模型参数的典型值 Table 1 Typical data of model parameters
A B Tj TM0 Pu Qu
0.5 0.3 2 1 2 2
表选项
3.2 辨识策略的实施

本文通过在Matlab中编程实现电铁冲击负荷模型的参数辨识.选取图 2所示实测数据作为模型激励和响应.该数据所反映交直型和交直交型电力机车混合负荷的特性，功率因素取为0.95.

令式(10)中K1=1、K2=1.经辨识得到的有功、无功功率和视在功率曲线如图 4所示.模型I参数辨识值见表 2.

表 2 模型I参数辨识值 Table 2 Parameter identification data of model I
参数 辨识值
L13.22
J5.74
R0.93
C13.88
Kzp0.27
C0.67
T′0.75
X′0.02
N2
Kjp0.38
Kp-712
Kq-452
表选项
图 4 模型Ⅰ仿真结果 Figure 4 Simulation results of model I
图选项

由图 4可以看出，模型能够反映实测功率的总体变化趋势，对于有功功率和无功功率均有较好的拟合效果，对于无功功率的拟合好于有功功率；该模型能够较为准确地捕捉负荷产生主动功率冲击的时刻，能够正确地反映负荷的冲击特性.

然而，该模型对于负荷产生极大的短时功率冲击之后的微小功率调整阶段的描述不太理想，仿真曲线波动幅度明显大于实际曲线.通过分析，认为主要原因在于实测电压受其他因素影响，在电铁负荷功率处于动态稳定的状态下仍然持续较大幅度的波动，导致模型辨识出现误差.参数Kp和Kq绝对值较大，反映出电铁负荷对系统造成较大的功率冲击，对系统母线电压影响相对较小.

4 电铁冲击负荷模型的改进 4.1 功率需求主动性的数学描述

电气化铁路系统负荷的主动冲击特性主要体现在电力机车的行进过程中.电力机车实际行进过程中对功率的主动需求分为两个方面：

1) 启动和加速过程：电力机车在启动和加速过程中，牵引电机负载转矩会发生极大的变化.

2) 跨电分相：电力机车以较大的速度跨电分相时，会在瞬间给电力系统功率冲击.

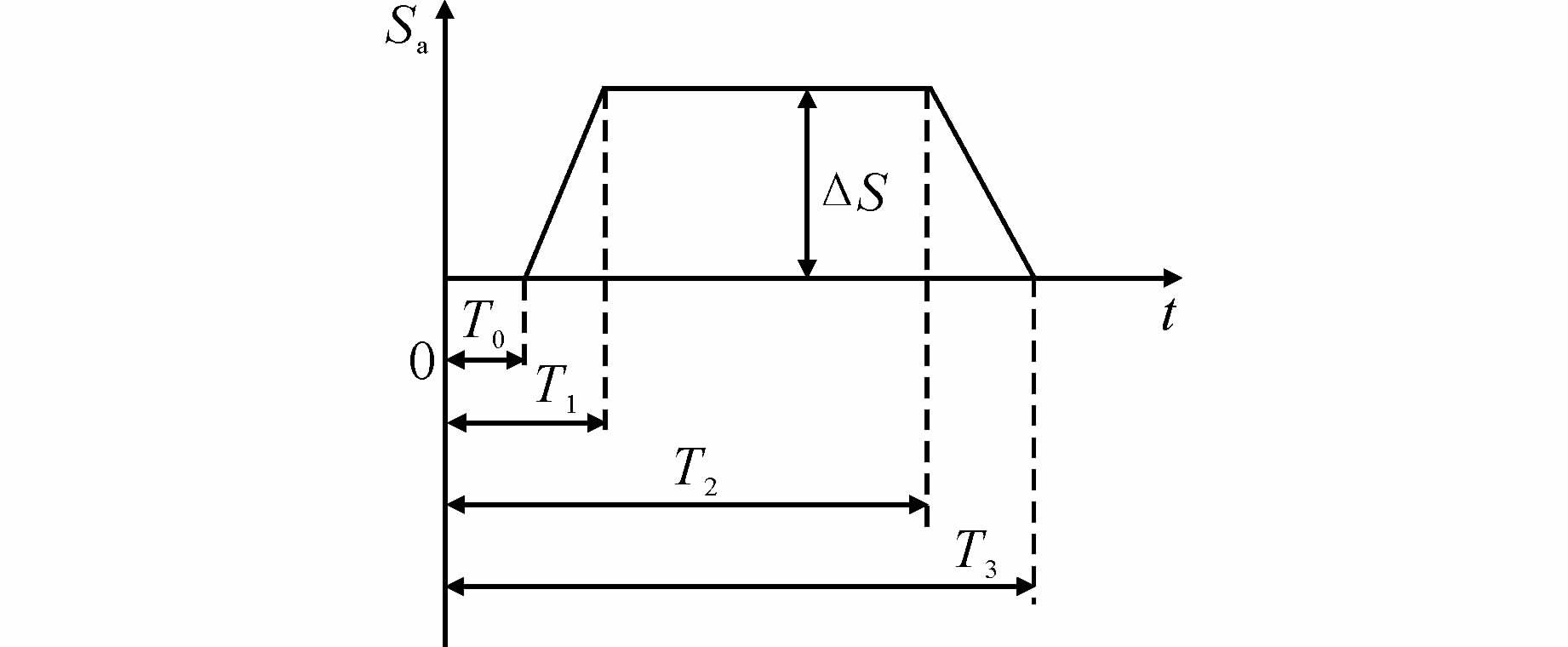
本文首先将机车的功率主动需求等效为近似梯形的功率变化过程，如图 5所示；然后通过系统辨识确定该梯形功率变化曲线的数学结构.

图 5 主动性功率需求模型 Figure 5 Active power demand model
图选项

图 5中，纵轴表示视在功率，横轴表示时间(采样点).ΔS、T0~T3分别为待辨识参数，功率主动性需求可以利用阶跃函数的数学模型表示如下：

$\left\{ \begin{align} & {{S}_{smooth}}(t)=\Delta s*[h(t-{{T}_{1}})-h(t-{{T}_{2}})] \\ & {{S}_{up}}(t)=\Delta s*(t-{{T}_{0}})/({{T}_{1}}-{{T}_{0}})*[h(t-{{T}_{0}})-h(t-{{T}_{1}})] \\ & {{S}_{down}}(t)=\Delta s*(t-{{T}_{3}})/({{T}_{3}}-{{T}_{2}})*[h(t-{{T}_{3}})-h(t-{{T}_{2}})] \\ \end{align} \right.$    (11)
${{S}_{a}}(t)={{S}_{smooth}}(t)+{{S}_{up}}(t)+{{S}_{down}}(t)$    (12)

其中:h(t)为单位阶跃函数；Ssmooth(t)、Sup(t)和Sdown(t)分别为图 5中曲线水平、上升和下降部分对应的功率；Sa(t)为三者在时间轴上叠加后的综合冲击功率.如果分别考虑有功功率和无功功率冲击，可利用式(12)通过功率因素φ求得.

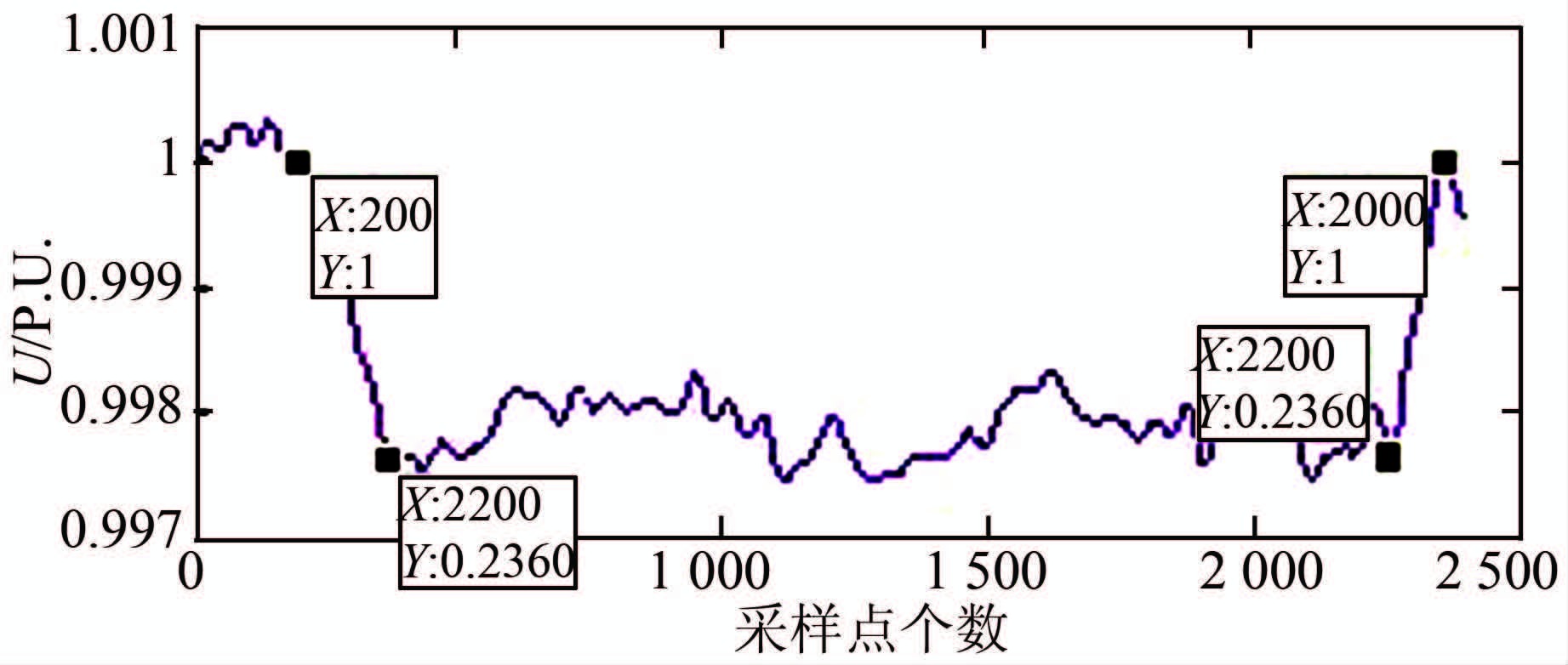
4.2 改进电铁冲击负荷模型

结合图 2激励和响应曲线进行特征点分析.在第200~370个采样点期间电力机车完成较大功率冲击之后基本保持最大功率匀速行驶，直至第2 260个采样点时刻实测机车功率开始陡降，对应时刻的母线电压曲线分析如图 6所示.

图 6 母线电压曲线 Figure 6 The curve of busbar voltage
图选项

在第200个采样点之前，机车负荷功率较为平稳；在第200~370个采样点之间机车负荷显示出其强冲击特性；在第370~2 260个采样点之间机车负荷在高功率需求点附近作较小的功率需求调整；在第2 260~2 360个采样点之间机车负荷显示出其强冲击特性；之后，机车负荷表现平稳.

基于以上分析，将式(10)描述的功率特性与式(12)描述的功率特性叠加，用以改进对于电铁冲击负荷的数学描述.具体来讲，以U(X,Y)表示实测母线电压曲线图上坐标点.设图 6中标注的四个特征采样点按时间顺序依次为U(X0,Y0)、U(X1,Y1)、U(X2,Y2)和U(X3,Y3)，令改进的电铁冲击负荷模型为M，式(10)所示负荷模型为M1、式(12)所示模型为M2，则以下式表示改进的电铁冲击负荷模型结构:

$M=\left\{ \begin{align} & {{M}_{1}}\ \ \ \ \ \ \ \ \ \ \ (X\le {{X}_{0}},X\ge {{X}_{3}}) \\ & {{M}_{1}}+{{M}_{2}}\ \ \ ({{X}_{0}}<X<{{X}_{3}}) \\ \end{align} \right.$    (13)

其中：X0=T0，X1=T1，X2=T2，X3=T3，为待辨识参数.通过实施先前制定的参数辨识策略可得到完整的模型.

4.3 模型的实现与分析

为叙述方便，称式(10)为模型Ⅰ，式(13)为模型Ⅱ.同样采用图 2所示实测数据对模型Ⅱ进行辨识，并与模型Ⅰ的仿真结果进行比较分析.模型Ⅱ的仿真结果如图 7所示.由于模型Ⅱ并不改变模型Ⅰ对于冲击负荷的负荷特性描述，因此在模型Ⅰ的参数基础上仅需辨识表 3所示7个参数.适应度函数值计算结果见表 4.

图 7 模型Ⅱ仿真结果 Figure 7 Simulation results of model Ⅱ
图选项
表 3 模型Ⅱ参数辨识值 Table 3 Parameter identification data of model Ⅱ
Kp Kq ΔS T0 T1 T2 T3
-153 -66 3.63 205 377 2 277 2 392
表选项
表 4 适应度函数值 Table 4 Fitness function data
负荷模型 适应度函数值J
模型Ⅰ 0.830 2
模型Ⅱ 0.013 2
表选项

由以上结果可以看出，模型Ⅱ相对于模型Ⅰ有更好的拟合精度.认为主要原因如下：模型Ⅰ的功率需求完全取决于电网母线电压，而实测PCC点电压除受牵引供电系统负荷影响之外，还取决于其他用电负荷的变化.也就是说，实测数据中既包含电力机车冲击特性，又包含其负荷特性，还包含了一定量的其他负荷的特性.因此，这种情况下可能会导致模型陷入围绕电压扰动的局部过度拟合状态，引起拟合误差；模型Ⅱ在模型Ⅰ的基础上在功率冲击极大的时刻加入主动性需求功率的解析表达，使模型表现出更好的冲击特性.一方面，这种主动性功率并不依赖于系统电压，它由机车运行的工况决定，有效摆脱了其他负荷对于系统母线电压的影响而造成的辨识误差.另一方面，主动性需求功率的加入拓展了模型对于冲击特性描述的尺度，使得原有模型更专注于微小的功率变化描述，有利于减小Kp、Kq的取值.模型Ⅱ对冲击特性有更好的拟合的同时保留了原有模型对于负荷特性和冲击特性的描述能力.

模型Ⅰ相对于模型Ⅱ有更好的泛化能力.电铁冲击负荷具有很强的随机性，功率冲击的幅值、发生时间和持续时间各不相同，不具备严格的周期性变化特点.模型Ⅱ无法实时而准确地跟踪负荷产生主动性功率冲击的特征点.

因此，模型Ⅰ适合精度要求不高的情况下做负荷预测和电气化铁路发展规划；模型Ⅱ可用于对模型Ⅰ的辨识结果作修正，适合分析电气化铁路冲击负荷对电网的影响.

5 结论

电气化铁路牵引供电负荷是时变的、在空间上移动的负荷，是动态的、非线性的负荷.传统的负荷模型对电铁时变负荷缺乏足够的描述能力.本文首先对电网侧PCC处实测数据进行预处理.然后将电气化铁路牵引供电负荷看作一个“灰色系统”，面向电网PCC点建立交直型和交直交型电力机车的综合负荷特性模型，并针对冲击负荷的主动性特点对模型作改进.最后，通过参数辨识和算例分析验证模型的正确性和有效性.

参考文献
[1] 李欣然, 张广东, 朱湘友, 等. 牵引供电系统综合负荷模型结构[J]. 电力系统自动化, 2009, 33(16): 71–76.
Li Xinran, Zhang Guangdong, Zhu Xiangyou, et al. A load model of traction power supply system[J]. Automation of Electric Power Systems, 2009, 33(16): 71–76.
[2] 周盛. 高速铁路牵引负荷建模及分析[D]. 杭州: 浙江大学, 2011.
Zhou Sheng. Load modeling and analysis of high-speed railway traction load[D] . Hangzhou:Zhejiang University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10335-1011067945.htm
[3] 黄石柱, 李建华, 赵娟, 等. 基于Matlab的电力列车数字仿真模型[J]. 电力系统自动化, 2002, 26(2): 51–55.
Huang Shizhu, Li Jianhua, Zhao Juan, et al. Matlab based digital simulation model for electrical locomotive[J]. Automation of Electric Power Systems, 2002, 26(2): 51–55.
[4] 张俊杰, 肖湘宁, 尹忠东, 江佩斯. 基于PSCAD/EMTDC的SS6B型电力机车仿真模型研究[J]. 机车电传动, 2008(06): 27–29.
Zhang Junjie, Xiao Xiangning, Yin Zhongdong, Jiang Peisi. Simulation model of SS6B electrical locomotive based on PSCAD/EMTDC[J]. Electric Drive for Locomotives, 2008(06): 27–29.
[5] 刘瑜. 电气化铁路牵引网的仿真分析[D]. 济南: 山东大学, 2007.
Liu Yu. Simulation of electrified railway traction network[D] . Jinan:Shandong University, 2007.
[6] 盛彩飞. 电力机车和动车组谐波电流的仿真研究[D]. 北京: 北京交通大学, 2009.
Sheng Caifei. Research on harmonic current simulation of electrical locomotives and EMUs[D]. Beijing:Beijing Jiaotong University, 2009. http://www.oalib.com/references/17579080
[7] Hegazy Y G, Salama M M A. Probabilistic representation of harmonic currents produced by AC/DC static power converters[C]// Proceedings of Industry Applications Conference, Orlando, 1995:1689-1695.
[8] Morrison R E, Clark A D. Probabilistic representation of harmonic currents in AC traction systems[J]. IEE Proceedings of Electric Power Applications, 1984, 131(5): 113–119.
[9] Abrahamsson L, Soder.Basic L modeling for electric traction systems under uncertainty[C]// Proceedings of the 41st International Conference of UPEC, Newcastle, 2006:252-256.
[10] 韩奕, 李建华, 黄石柱, 夏道止. SS4型电力机车的动态模型及随机谐波电流计算[J]. 电力系统自动化, 2001, 25(4): 31–36.
Han Yi, Li Jianhua, Huang Shizhu, Xia Daozhi. The mechanism of mitigating Sub-synchronous resonance by thyristor-controlled series compensation[J]. Automation of Electric Power Systems, 2001, 25(4): 31–36.
[11] 鞠平, 马大强. 电力系统负荷建模[M]. 北京: 中国电力出版社, 2008.
Ju Ping, Ma Daqiang. Load Modeling of Power System[M]. Beijing: China Electric Power Press, 2008.
[12] 鞠平. 电力系统建模理论与方法[M]. 北京: 科学出版社, 2010.
Ju Ping. Power System Modeling Theory and Method[M]. Beijing: Science Press, 2010.
[13] 程颖, 鞠萍, 吴峰. 负荷模型参数辨识的粒子群优化法及其与基因算法比较[J]. 电力系统自动化, 2003, 27(11): 25–29.
Cheng Ying, Ju Ping, Wu Feng. PS algorithm in load parameter identification and its comparison with genetic algorithm[J]. Automation of Electric Power System, 2003, 27(11): 25–29.
[14] Shi Y, Eberhart R. Empirical study of particle swarm optimization[C]// International Conference on Evolutionary Computation. Washington, USA: IEEE, 1999:1945-1950.
[15] Fukuyama Y, Yoshida H. A particle swarm optimization for reactive power and voltage control in electric power systems[C]// Proc. Congress on Evolutionary Computation 2001, Seoul (Korea), 2001.