武汉大学学报(工学版)   2016, Vol. 49 Issue (5): 714-719

文章信息

宣腾, 李锦辉, 李典庆, 宋磊
XUAN Teng, LI Jinhui, LI Dianqing, SONG Lei
基于普通克里金法的勘探位置优化方法
Optimization of locations of site investigation using ordinary Kriging method
武汉大学学报(工学版), 2016, 49(5): 714-719
Engineering Journal of Wuhan University, 2016, 49(5): 714-719
http://dx.doi.org/10.14188/j.1671-8844.2016-05-012

文章历史

收稿日期: 2016-04-01
 Abstract              PDF               Figures               Tables
引用本文 0
宣腾, 李锦辉, 李典庆, 宋磊. 基于普通克里金法的勘探位置优化方法[J]. 武汉大学学报(工学版), 2016, 49(5): 714-719.
XUAN Teng, LI Jinhui, LI Dianqing, SONG Lei. Optimization of locations of site investigation using ordinary Kriging method[J]. Engineering Journal of Wuhan University, 2016, 49(5): 714-719.
基于普通克里金法的勘探位置优化方法
宣腾1, 李锦辉1, 李典庆2, 宋磊1     
1. 哈尔滨工业大学深圳研究生院，广东 深圳 518055;
 2. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072
收稿日期: 2016-04-01
作者简介: 宣腾（1990-），女，硕士研究生，主要研究方向为岩土工程，E-mail:xteng1990@163.com.
通讯作者: 李锦辉（1978-），女，博导，副教授，主要从事岩土工程风险分析和海洋岩土工程等方面的研究，E-mail:jinhui.li@hit.edu.cn
基金项目: 国家自然科学基金（编号：51379053）; 水资源与水电工程科学国家重点实验室（武汉大学）开放研究基金项目（编号：2013B112）.
摘要: 采用普通克里金法探索优化新增地质勘探点的方法，通过优化勘探位置以尽量少的勘探数量获得最多的地质勘探信息.根据已有的地质勘探点利用普通克里金法对整个勘探区域进行预测，并计算预测值的标准差，将普通克里金标准差最大值所对应的位置设为新增勘探点的位置，以降低预测误差，使新增勘探信息的效用最大化.以澳大利亚国家软土试验中心在100 m×100 m的软土区得到的26个CPTU试验数据为例，利用提出的新增地质勘探点优化方法探讨了此方法的正确性和精度.
关键词： 普通克里金     优化     勘探     半变异函数     静力触探试验    
Optimization of locations of site investigation using ordinary Kriging method
XUAN Teng1, LI Jinhui1, LI Dianqing2, SONG Lei1     
1. School of Shenzhen Graduate, Harbin Institute of Technology, Shenzhen 518055, China;
 2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
Abstract: The method of optimizing new geological exploration will be explored using ordinary Kriging method to determine its optimal locations. According to existing site investigation, the parameters of interests are predicted using ordinary Kriging method over the whole site first. Then the standard deviations of the predicted values are evaluated to facilite the following optimization. Locations of the new site investigation are selected as the locations with maximum ordinary Kriging standard deviation in order to reduce the predicted error and maximize the value of new investigation. Finally, an example with 26 cone-penetration test undrained (CPTU) is performed to demonstrate the optimization method. These tests were performed by the National Soft Soil Field Testing Facility of Australia in an area of 100 m×100 m; the rationality and the accuracy of the method are discussed.
Key words: ordinary Kriging method     optimization     site investigation     semivariogram     cone penetration tests    

克里金插值法(Kriging)又称空间局部插值法，是法国地质统计学家Matheron创立并发展起来的，以纪念南非矿业工程师D. G. Krige在1951年首次将统计学技术运用到地矿评估中[1-3]，该方法综合考虑了区域化变量的结构性和随机性，是估计未采样区域土体参数的重要方法之一.

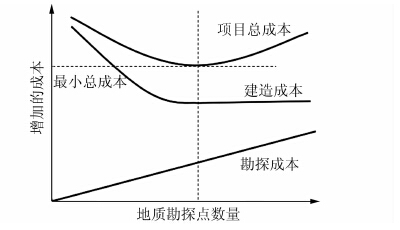
在建筑物建设之前，首先需要对建筑地区进行工程地质勘探，目的是了解工程地质情况，对建筑区域的地质做出评价，为建筑工程的可行性研究、设计和施工等方面提供可靠的地质依据[4].地质勘探点的数量对建造成本和项目总成本有较大影响，如图 1所示随着地质勘探点数量的增加，会得到更加详细的地质资料，有利于建筑设计，节约建造成本和项目总成本.但当勘探点增加到一定数量时，地质资料的详细程度将不会增加太多，对建筑设计不会有太大影响，建造成本几乎不变，勘探成本增加较大，因此项目总成本也会增加.项目总成本最小时对应的勘探点数量即为最优勘探点数量.由于成本涉及的因素较多，本文不以勘探成本和项目总成本作为优化目标，而是聚焦于优化新增地质勘探点的位置，以达到可以利用较少的勘探点得到较多的地质信息的目的.本文基于普通克里金法，结合现场CPTU试验数据，提出了一种新增地质勘探点的优化方法.

图 1 地质勘探点数量与成本的关系 Figure 1 Relationship between quantity and cost of site investigation
图选项
1 基于普通克里金的地质勘探优化方法

根据已有的地质勘探信息优化新增勘探点时，新增勘探点位置的选取应以获取更多土体参数信息为目的.克里金法与其他估值方法(如反距离加权法、样条插值法等)相比具有的显著优点就是该法不仅能对未知区域进行估值，还可以提供估计值的误差，从而得到更多的土体参数信息.

克里金插值法是利用已知的区域化变量的原始数据和变异函数理论，对非样本点值进行线性无偏、最优估计[5].克里金插值法中最简单、常用的是普通克里金法[6](Ordinary Kriging，OK).

适用于普通克里金法的随机变量Z(x)需满足固有假设的条件[7,8]：

1) 随机变量的均值存在并与距离h无关：

$E[Z(x+h)-Z(x)]=0;$

2) 距离为h时，增量[Z(x+h)-Z(x)]的方差存在，且该方差与x无关：

$Var[Z(x+h)-Z(x)]=2\gamma (h).$

式中：Z(x)、Z(x+h)分别为x和x+h位置处的观测值；E[·]为均值；Var[·]为方差；γ(h)为距离h对应的半变异函数值.

假设已知勘探点的数据值为Z(x1)，Z(x2)，…,Z(xn)，当这些数据值满足上述条件(1)和(2)时，勘探数据的半变异函数值(Semivariogram)的计算公式如下[9]：

$\gamma (h)=\frac{1}{2{{N}_{h}}}\sum\limits_{i=1}^{{{N}_{h}}}{{{[Z({{x}_{i}}+h)-Z({{x}_{i}})]}^{2}}}$    (1)

式中：h为xi点和xi+h点之间的距离；Nh为距离为h的勘测数据点对的个数.

普通克里金法的估值公式为[10]

${{Z}^{*}}({{x}_{0}})=\sum\limits_{i=1}^{n}{{{\lambda }_{i}}}Z({{x}_{i}})$    (2)

式中：Z*(x0)为在x0位置的估计值；n为观测点的个数；Z(xi)为在xi位置的观测值；λi为分配给Z(xi)的权重.

根据克里金法的要求，估计值需满足两个条件[11]：估计值应该是无偏的，即平均估计误差为0；估计值误差的方差最小.由这两个条件可推导出普通克里金的线性方程组[12, 13]：

$\left[ \begin{matrix} {{\gamma }_{11}} & {{\gamma }_{12}} & \cdots & {{\gamma }_{1n}} & 1 \\ {{\gamma }_{21}} & {{\gamma }_{22}} & \cdots & {{\gamma }_{2n}} & 1 \\ \vdots & \vdots & \vdots & \vdots & 1 \\ {{\gamma }_{n1}} & {{\gamma }_{n2}} & \cdots & {{\gamma }_{nn}} & 1 \\ 1 & 1 & \cdots & 1 & 0 \\ \end{matrix} \right]*\left[ \begin{matrix} {{\lambda }_{1}} \\ {{\lambda }_{2}} \\ \vdots \\ {{\lambda }_{n}} \\ \mu \\ \end{matrix} \right]=\left[ \begin{matrix} \gamma ({{x}_{1}},{{x}_{0}}) \\ \gamma ({{x}_{2}},{{x}_{0}}) \\ \vdots \\ \gamma ({{x}_{n}},{{x}_{0}}) \\ 1 \\ \end{matrix} \right]$    (3)

式中：γij(i,j=1,2,…,n)为i位置的勘测数据和j位置的勘测数据之间的半变异函数值；λi(i=1,2,…,n)为分配给i位置勘测数据的权重系数；γ(xi,x0)(i=1,2,…,n)为i位置的勘测数据和预测点之间的半变异函数值；μ为拉格朗日常数.

普通克里金方差σOK2的公式为[14]

$\sigma _{OK}^{2}=\sum\limits_{i=1}^{n}{{{\lambda }_{i}}}\gamma ({{x}_{i}},{{x}_{0}})+\mu $    (4)

由于克里金法与其他估值法相比突出的优点是可以提供估值精度，所以本文提出的新增地质勘探点优化方法是先根据已有的地质勘探点利用普通克里金法对勘探区域内其他未知区域值进行估计并计算其OK标准差.比较OK标准差的大小，OK标准差越大表明所对应的位置上的估值误差越大，即估值与真实值相差较大.所以新增钻孔应该在OK标准差最大的位置.

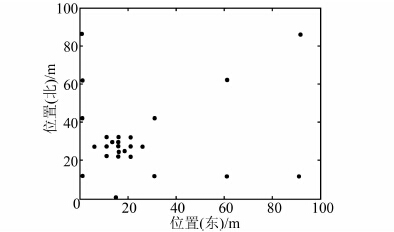
2 算例分析

为了探索原位试验和实验室试验的相关关系、确定工程参数以及评估土体的变异性，国家软土现场实验中心(The National Soft Soil Field Testing Facility)在澳大利亚新南威尔士州巴利纳附近的软土区做了多种类型的试验：CPT、CPTU、VST、T-bar等[15].图 2所示为其中26个CPTU钻孔的位置，实验总占地面积为100 m×100 m.在每个CPTU试验中都测量出每隔0.02 m深度的锥尖阻力、侧摩阻力和孔隙水压力.

图 2 26个CPTU钻孔的位置 Figure 2 Locations of 26 CPTU drilling holes
图选项

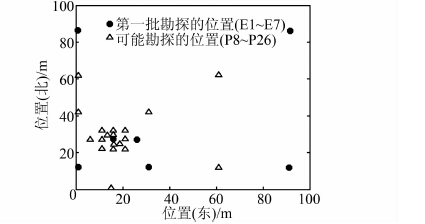
假设在该软土区域100 m×100 m内要建设公共设施，现已做了第一批地质勘探点，即如图 3所示的7个CPTU试验，并测得相关土体参数：锥尖阻力、侧摩阻力和孔隙水压力.但这7个CPTU试验所测的数据不足以准确地描述整个区域的土体参数分布，故决定在未钻孔区域再选择2个位置进行勘探. 本文以2 m深度的锥尖阻力值为区域化变量，利用普通克里金法在未钻孔区域优化新增钻孔的位置.为了方便验证估计值的准确性，本文利用7个位置的CPTU数据作为已有的第一批勘探数据，把剩余的19个位置作为可能的勘探位置(如图 3所示)，即估计钻孔位，从这19个位置中选出2个位置作为新增勘探点，比较预测值与试验值的差值，选择能提供较准确估计值的钻孔位，建立新增勘探位置的优化准则.

图 3 第一批勘探和可能勘探的位置 Figure 3 Locations of first batch of exploration and possible exploration
图选项

根据公式(1)以及第一批勘探的7个CPTU试验测得的2 m深度处的锥尖阻力值计算观测数据的变异函数值，画出以间隔距离(h)为x轴、半变异函数值为y轴的散点图，并对该散点图进行模型曲线拟合.常用的变异函数(协方差)模型有球形模型：

$\gamma (h)=\left\{ \begin{matrix} {{C}_{0}}+C(\frac{3h}{2a}-\frac{{{h}^{3}}}{2{{a}^{3}}})\begin{matrix} {} & 0\le h\le a \\ \end{matrix} \\ {{C}_{0}}+C\begin{matrix} {} & h>a \\ \end{matrix} \\ \end{matrix} \right.$    (5)

指数模型：

$\gamma (h)={{C}_{0}}+C\left( 1-\exp \left( -\frac{3h}{a} \right) \right)$    (6)

高斯模型：

$\gamma (h)={{C}_{0}}+C\left( 1-\exp \left( -\frac{3{{h}^{2}}}{{{a}^{2}}} \right) \right)$    (7)

立方体模型：

$\gamma (h)=\left\{ \begin{matrix} {{C}_{0}}+C(\frac{7{{h}^{2}}}{{{a}^{2}}}-\frac{35{{h}^{3}}}{4{{a}^{3}}}+\frac{7{{h}^{5}}}{2{{a}^{5}}}-\frac{3{{h}^{7}}}{4{{a}^{7}}})\begin{matrix} {} & 0\le h\le a \\ \end{matrix} \\ {{C}_{0}}+C\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} {} & {} \\ \end{matrix} & \begin{matrix} \begin{matrix} \begin{matrix} {} & {} \\ \end{matrix} & {} \\ \end{matrix} & {} \\ \end{matrix} \\ \end{matrix} & {} \\ \end{matrix} & {} \\ \end{matrix} & {} \\ \end{matrix} & h>a \\ \end{matrix} \\ \end{matrix} \right.$    (8)

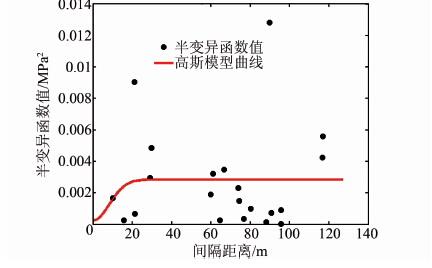
式中：C0为块金值(nugget)；C为偏基台值(partial sill)；C0+C为基台值(sill)；h为分离距离(lag)；a为变程(range).本文利用计算的半变差函数值与拟合函数之间的残差平方和来评价不同变异函数模型的拟合效果.由于利用式(1)计算出的半变差函数值与相同分离距离的高斯模型函数计算出的半变异函数值的差的平方和最小(2.053 9×10-4)，所以最终选取块金值C0为0.000 23 MPa2、变程a为20.48 m、基台值C0+C为0.002 8 MPa2的高斯模型，拟合曲线如图 4所示.残差平方和越小，说明所用半变异函数模型越能描述数据之间的相关性.当数据量有限时，半变异函数的数据会比较离散，这时可以从不同的模型函数拟合结果中选取残差平方和较小的模型，以得到相对较好的权重系数和预测值.得到高斯模型表达式后，分别计算任意两个样本点之间的半变异函数值和预测点与观测点之间的半变异函数值，然后把计算结果代入到普通克里金方程组(3)中，则可以得到权重系数λi和拉格朗日常数μ，进而计算出锥尖阻力的预测值.整个区域的锥尖阻力的预测值和普通克里金标准差如图 5所示.

图 4 半变异函数值及高斯模型 Figure 4 Semivariogram and Gaussian model
图选项
图 5 基于7个观测点的预测锥尖阻力值及其标准差 Figure 5 The predicted values of cone penetration resistance and its standard deviation based on 7 observation points
图选项

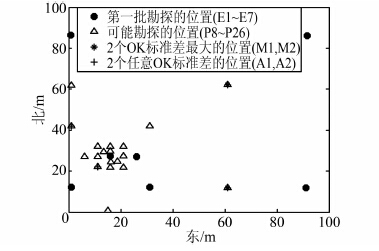
分别计算19个可能的勘探位置处的锥尖阻力预测值以及普通克里金标准差，并比较不同位置计算出来的标准差的大小.选择剩余19个可能的勘探位置处标准差最大的2个位置作为新增钻孔点的位置(如图 6所示).

图 6 新增钻孔位置示意图 Figure 6 The diagram of new drilling positions
图选项

作为对比，本文又从其他17个非标准差最大的位置中选择了2个任意标准差的位置(如图 6所示)，将这2个位置作为新增钻孔点的位置，把第一批勘探的7个CPTU试验和2个任意标准差位置处的CPTU试验所测得的锥尖阻力值作为观测数据，结合普通克里金法，重新拟合变异函数模型、曲线(利用上文所述比较方法，最终选择块金值C0为0.000 015 MPa2、基台值C0+C为0.002 4 MPa2、变程a为22.54 m的立方体模型)、预测其他未知区域处的锥尖阻力值以及计算普通克里金标准差(如图 7所示).

图 7 新增任意2个观测点后锥尖阻力的预测值及其标准差 Figure 7 Predicted values and standard deviation of one penetration resistance after addition of arbitrary 2 observation points
图选项

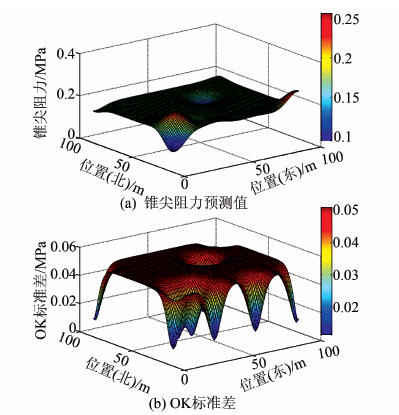
当以第一批勘探的7个CPTU试验和2个标准差最大位置处的CPTU试验所测得的锥尖阻力值作为观测数据时，利用普通克里金法，再次拟合变异函数模型曲线(利用上文所述比较方法，最终选择块金值C0为0.000 13 MPa2、基台值C0+C为0.002 3 MPa2、变程a为17.95 m的高斯模型)、预测其他未知区域处的锥尖阻力值以及计算普通克里金标准差(如图 8所示).

图 8 新增标准差最大的2个钻孔点后锥尖阻力的 预测值及其标准差 Figure 8 Predicted values and standard deviation of one penetration resistance after addition of 2 observation points corresponding to maximum standard deviation
图选项

最后，把剩余15个估计钻孔位处的CPTU试验所测得的锥尖阻力值作为对比值，分别与7个数据、9个数据(含2个标准差最大位置处的数据)、9个数据(含2个任意标准差位置处的数据)作为观测数据预测出的这15个位置处的锥尖阻力预测值(表 1)进行比较.

表 1 不同观测数据预测出的结果比较 Table 1 Comparison of predicted results with different observation data
钻孔位 试验值/MPa 利用7个观测数据的预测值/MPa 利用9个观测数据(含2个任意OK标准差)的预测值/MPa 利用9个观测数据(含2个OK标准差最大)的预测值/MPa
E1 0.149 7 - - -
E2 0.095 3 - - -
E3 0.193 7 - - -
E4 0.255 3 - - -
E5 0.187 3 - - -
E6 0.171 9 - - -
E7 0.229 7 - - -
M1(P8) 0.139 7 0.181 9 0.173 1 -
M2(P9) 0.182 1 0.182 1 0.173 1 -
A1(P10) 0.128 3 0.184 9 - 0.178 0
A2(P11) 0.182 0 0.204 7 - 0.202 9
P12 0.200 4 0.214 8 0.201 9 0.214 0
P13 0.184 4 0.200 8 0.178 3 0.194 6
P14 0.169 1 0.224 4 0.206 6 0.216 0
P15 0.179 4 0.232 2 0.225 4 0.228 7
P16 0.253 3 0.223 6 0.217 3 0.223 8
P17 0.204 8 0.229 3 0.229 8 0.227 9
P18 0.209 6 0.224 3 0.221 9 0.220 4
P19 0.225 0 0.216 0 0.214 3 0.216 4
P20 0.204 6 0.199 3 0.193 6 0.198 0
P21 0.192 5 0.200 1 0.202 1 0.198 4
P22 0.219 0 0.174 3 0.172 3 0.173 3
P23 0.171 1 0.177 0 0.172 0 0.174 8
P24 0.179 7 0.181 5 0.173 1 0.176 8
P25 0.215 7 0.226 1 0.210 2 0.222 2
P26 0.193 3 0.202 9 0.206 0 0.203 3
表选项
3 结果分析

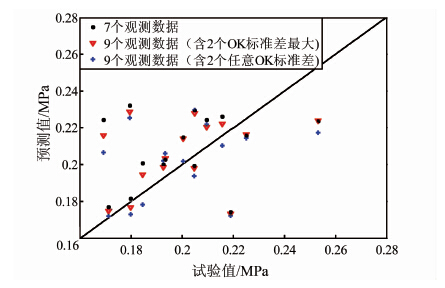
通过表 1分析可知，当新增2个孔位是标准差最大位置时，预测出来的15个估计钻孔位处的锥尖阻力值中的绝大部分都比只利用7个观测数据预测出来的15个估计钻孔位处的锥尖阻力值更接近试验值；当新增2个孔位是任意标准差位置时，预测出来的15个估计钻孔位处的锥尖阻力值中的绝大部分也都比只利用7个观测数据预测出来的15个估计钻孔位处的锥尖阻力值更接近试验值；当新增2个孔位是标准差最大位置时，预测出来的15个估计钻孔位处的锥尖阻力值中的绝大部分都比新增2个孔位是任意标准差位置预测出来的15个估计钻孔位处的锥尖阻力值更接近试验值.根据不同观测数据计算出来的预测值与试验值的对比关系如图 9所示.

图 9 预测值与试验值的对比 Figure 9 Comparison between predicted values and test values
图选项

通过计算可知，当新增2个孔位是标准差最大位置时，计算出来的15个估计钻孔位处的普通克里金标准差几乎全部比只利用7个观测数据计算出来的相同位置的普通克里金标准差小；当新增2个孔位是任意标准差位置时，计算出来的15个估计钻孔位处的普通克里金标准差绝大部分比只利用7个观测数据计算出来的相同位置的普通克里金标准差 小；当新增2个孔位是标准差最大位置时，计算出来的15个估计钻孔位处的普通克里金标准差绝大部分比利用新增2个孔位是任意标准差位置计算出来的相同位置的普通克里金标准差小.因此，当新增孔位选取克里金标准差最大的位置时，其得到的锥尖阻力值最精确.

4 结论

本文提出了一种基于普通克里金法的勘探新增位置优化的方法，通过比较不同位置观测数据的预测结果，得到以下结论：

1） 当在已有的、较少的勘探信息的基础上新增钻孔时，通过普通克里金法利用新增钻孔后的勘探信息预测未知区域处的值大部分比只利用原有勘探信息预测的相同位置处的值更接近试验值，即新增钻孔有利于得到更多地质信息．

2） 当在已有的、较少的勘探信息的基础上新增钻孔时，通过普通克里金法利用新增钻孔后的勘探信息计算未知区域处的OK 标准差大部分比只利用原有勘探信息计算的相同位置处的OK 标准差更小．

3） 当新增钻孔位为OK 标准差最大位置时，通过普通克里金法利用新增钻孔后的勘探信息预测出的未知区域处的值大部分比当新增钻孔位为相同数量的任意OK 标准差位置时预测出的相同位置处的值更接近试验值，即此时得到更精确的地质信息．

4） 新增钻孔位为OK 标准差最大位置时，其新增勘探信息的效用比新增钻孔为任意位置的效用大，所以新增钻孔位应选取OK 标准差最大所对应的位置．

参考文献
[1] 杨雪峰, 胡长青. 普通克里金法在海水温度剖面插值中的应用[J]. 声学技术, 2015, 34(5): 385–388.
Yang Xuefeng, Hu Changqing. Application of ordinary Kriging method in the interpolation for seawater temperature profile[J]. Technical Acoustics, 2015, 34(5): 385–388.
[2] 李振海, 方亿锋. 基于克里金法重力数据插值的研究[J]. 测绘信息与工程, 2010, 35(1): 42–43.
Li Zhenghai, Fang Yifeng. Research of gravity data's interpolation by ordinary Kriging method[J]. Journal of Geomatics, 2010, 35(1): 42–43.
[3] Davis John C. Statistics and Data Analysis in Geology[M]. New York : John Wiley&Sons, 2002.
[4] 罗维刚, 王斐, 方有珍, 等. 地质勘探井点布局优化问题的研究[J]. 甘肃科学学报, 2005, 17(2): 76–79.
Luo Weigang, Wang Fei, Fang Youzhen, et al. The optimal layout of geological prospecting well grids[J]. Journal of Gansu Sciences, 2005, 17(2): 76–79.
[5] 张仁铎. 空间变异理论及应用[M]. 北京: 科学出版社, 2005.
Zhang Renduo. Spatial Variability: Theory and Application[M]. Beijing: Science Press, 2005.
[6] 刘强, 陶钧, 刘旭, 等. 基于克里金插值的磁法数据格网化研究[J]. 河南科学, 2013, 31(7): 1039–1044.
Liu Qiang, Tao Jun, Liu Xu, et al. Study on the gridding of magnetic method data based on interpolation principle of Kriging[J]. Henan Science, 2013, 31(7): 1039–1044.
[7] Miller J, Franklin J, Aspinall R. Incorporating spatial dependence in predictive vegetation models[J]. Ecological Modelling, 2007, 202(3): 225–242.
[8] Eldeiry A, Garcia L A. Detecting soil salinity in alfalfa fields using spatial modeling and remote sensing[J]. Soil Science Society of America Journal, 2008, 72(1): 201–211. DOI:10.2136/sssaj2007.0013
[9] 杨阳.克里金储层预测技术及应用[D].青岛:中国石油大学,2007.
Yang Yang. Reservoir prediction technology and application using Kriging method[D]. Qingdao: China University of Petroleum, 2007.
[10] 李晓军, 张振远. 基于指示和普通克里金的不连续地层厚度估计方法[J]. 岩土力学, 2014, 35(10): 2881–2887.
Li Xiaojun, Zhang Zhenyuan. A combined indicator-ordinary Kriging method for estimating thickness of discontinuous geological strata[J]. Rock and Soil Mechanics, 2014, 35(10): 2881–2887.
[11] 李莉, 胡建平. 克里金插值算法在等高线绘制中的应用[J]. 天津城市建设学院学报, 2008, 14(1): 68–71.
Li Li, Hu Jianping. Application of Kriging interpolation in contour creation[J]. Journal of Tianjin Institute of Urban Construction, 2008, 14(1): 68–71.
[12] 王长虹, 朱合华, 钱七虎. 克里金算法与多重分形理论在岩土参数随机场分析中的应用[J]. 岩土力学, 2014, 35(2): 386–392.
Wang Changhong, Zhu Hehua, Qian Qihu. Application of Kriging methods and multi-fractal theory to estimate geotechnical parameters spatial distribution[J]. Rock and Soil Mechanics, 2014, 35(2): 386–392.
[13] 陈宝政, 蔡德利. 普通Kriging插值算法研究[J]. 测绘与空间地理信息, 2009, 32(3): 7–9.
Chen Baozheng, Cai Deli. Algorithm and application of Kriging[J]. Geomatics & Spatial Information Technology, 2009, 32(3): 7–9.
[14] Long Weishun. Research of Kriging estimate technology applied in the roller temperature field[J]. Jingdezhen: Jingdezhen Ceramic Institute, 2011.
[15] Li J, Cassidy M J, Huang J, et al. Probabilistic identification of soil stratification[J]. Géotechnique, 2016, 66(1): 16–26. DOI:10.1680/jgeot.14.P.242