武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 949-954

文章信息

周黎, 周莉, 张伟民, 张晓琴
ZHOU Li, ZHOU Li, ZHANG Weiming, ZHANG Xiaoqin
双足舞蹈机器人步态规划
Gait planning for biped dancing robot
武汉大学学报(工学版), 2016, 49(6): 949-954
Engineering Journal of Wuhan University, 2016, 49(6): 949-954
http://dx.doi.org/10.14188/j.1671-8844.2016-06-025

文章历史

收稿日期: 2016-05-17
 Abstract              PDF               Figures               Tables
引用本文 0
周黎, 周莉, 张伟民, 张晓琴. 双足舞蹈机器人步态规划[J]. 武汉大学学报(工学版), 2016, 49(6): 949-954.
ZHOU Li, ZHOU Li, ZHANG Weiming, ZHANG Xiaoqin. Gait planning for biped dancing robot[J]. Engineering Journal of Wuhan University, 2016, 49(6): 949-954.
双足舞蹈机器人步态规划
周黎1, 周莉1, 张伟民1, 张晓琴2     
1. 中国地质大学(武汉)，湖北 武汉 430074;
 2. 武汉晴川学院， 湖北 武汉 430204
收稿日期: 2016-05-17
作者简介: 周黎(1982-)，女，副教授，硕士生导师，研究方向为机器人步态设计，E-mail:541537007@qq.com.
通讯作者: 张伟民(1976-)，男，博士，副教授，研究方向为机电一体化及应用、检测技术、先进制造技术，E-mail:5411377@qq.com
摘要: 以双足舞蹈机器人为对象，建立系统的多自由度运动学模型，在此基础上开展舞蹈机器人正运动学和逆运动学分析，根据行走步长、步宽、步行周期等运动参数求解机器人各关节角度；引入三维倒立摆模型，结合零力矩点(Zero-Moment-Point, ZMP)稳定判据，对舞蹈机器人进行步态规划稳定性分析；最后，结合对舞蹈机器人的行走步态进行了仿真分析，得到了各个关节的角度值，可作为舞蹈机器人的输入控制参数.
关键词： 双足舞蹈机器人     逆运动学     ZMP     三维倒立摆     步态规划    
Gait planning for biped dancing robot
ZHOU Li1, ZHOU Li1, ZHANG Weiming1, ZHANG Xiaoqin2     
1. China University of Geosciences (Wuhan), Wuhan 430074, China;
 2. Wuhan Qingchuan University, Wuhan 430204, China
Abstract: The multi-degree of freedom kinematic model of the biped dancing robot has been established in this paper. The angles of the knee, hip and ankle have been solved by performing the kinematic and invert kinematic analyzing of the dancing robot with the given step width, step length, walking period, etc. The gait planning of the dancing robot has been proposed by introducing the three-dimensional invert pendulum model and employing the zero-moment point(ZMP) stability theory. The numerical simulations are carried out for special WS parameters in this paper and the value of each angle of the dancing robot obtained in this paper could be used as input for motion controlling.
Key words: biped dancing robot     invert kinematics     ZMP     three-dimensional invert pendulum     gait planning    

双足机器人涉及到多个学科，包括仿生学、机器人学、动力学及控制理论等[1]，为多种学科融合提供了理想的研究平台.该领域过去几十年取得了大量的成果，部分仿人[2, 3]和仿生[4]成果已开始应用到服务领域.双足舞蹈机器人属于娱乐机器人的范畴[5]，具有旺盛的市场需求.本文通过参考双足步行机器人的相关研究，对双足舞蹈机器人舞蹈动作中的稳定性问题及步态规划进行了深入研究.

双足机器人的研究最早始于20世纪60年代，比较典型的双足仿人机器人代表有早稻田大学的WABIAN[6]系列机器人、Sony公司的QRIO[7]、Honda公司的ASIMO[8]、HRP[9]系列机器人和Keio大学的Morph等.美国康奈尔大学在双足机器人的研究中通过研究仿人机器人的被动行走，以行走过程中能量最小为优化目标，研制出了一款被动步行机器人[10]，其特点是可以不需要任何额外力矩实现斜坡上行走，而在平地上双足步行时能量消耗非常少.美国大狗BigDog[11]的生产公司波士顿动力推出的两款仿人机器人Petman[12]和Atlas[13]是仿人机器人研究的一个里程碑，这两款仿人机器人利用液压作为驱动代替了传统的电力驱动.

在双足机器人的研究方面，双足步行机器人的研究已经很深入[14-17]，逐步转向应用.双足舞蹈机器人作为其典型应用，其应用的场合和工况相比较其他双足机器人略有不同，在步行稳定及步态规划方面有待进一步研究[18, 19].本文的主要研究内容包括以下方面： 1)建立双足舞蹈机器人的运动学模型，并对其进行正逆运动学分析，根据行走步长、步宽、步行周期等运动参数求解机器人各关节角度；2)基于ZMP稳定性理论，采用倒立摆模型，规划质心和足部轨迹，对双足舞蹈机器人进行稳定性分析；3)使用正、逆运动学仿真计算得到各个关节角度与角速度的时程曲线作为物理样机各关节的理想输入，从而实现舞蹈机器人的动作控制.

1 运动学建模与分析

双足舞蹈机器人腿部结构是仿照人腿的结构设计的.本文研究的机器人腿部机构主要由以下部分构成：一个连接架，两个上支撑架，两个下支撑架，两个支撑座以及连接它们的关节铰链.它具有12个自由度，一边6个.如果把机器人上躯体与连接架看成一个整体,那么就可以将整个舞蹈机器人简化为一个5连杆机构.

1.1 正运动学分析

已知广义坐标求解机器人各杆件和摆动腿末端的位姿参数即为机器人正运动学分析.在机器人运动学模型建立完成后，需要确定每个坐标系的参数.每一个局部坐标系上都固结了一个杆，只要确定局部坐标系在世界坐标系中的位置和姿态，就能确定对应的杆的位姿.每一个坐标系的原点在世界坐标系中的矢量称为位置，本文用p1表示；其三轴分别在世界坐标系的3个轴上的投影组成的3阶方阵成为姿态矩阵，本文用R1表示，因此对于一个坐标系∑i可以用齐次变换矩阵描述它在世界坐标系中的位姿，如下式所示：

${T_i} = \left[ {\begin{array}{*{20}{c}} {}&{{R_1}}&{}&{{p_1}}\\ 0&0&0&1 \end{array}} \right]$    (1)

机器人各连杆变换的齐次变换矩阵具体形式如下所示：

${^{i - 1}}_iT = \left[ {\begin{array}{*{20}{c}} {c{\theta _i}}&{ - s{\theta _i}}&0&{{l_{i - 1}}}\\ {s{\theta _i}c{\partial _{i - 1}}}&{c{\theta _i}c{\partial _{i - 1}}}&{ - s{\partial _{i - 1}}}&{ - {d_i} - s{\partial _{i - 1}}}\\ {s{\theta _i}s{\partial _{i - 1}}}&{c{\theta _i}s{\partial _{i - 1}}}&{c{\partial _{i - 1}}}&{{d_i}c{\partial _{i - 1}}}\\ 0&0&0&1 \end{array}} \right]$    (2)
$_n^0T = _1^0T_2^1T \ldots _n^{n - 1}T$    (3)

其中：θi为关节转角；∂i为连杆扭转角；li为连杆长度；di为连杆偏移量.若知道某个传动链的末端坐标系的位姿和各个传动环节坐标系间的相对位姿，就可以求出各个传动环节在世界坐标系中的位姿.

设局部坐标系∑j在其母坐标系∑i中的转动轴矢量为ai，原点的相对位置矢量为bi，关节角为θi.其中，关节轴矢量是描述连杆相对于母连杆转动的单位矢量，其方向由右手法则确定，相对位置矢量是描述一个局部坐标系原点在其连杆坐标系中位置的矢量，这两个量都是常向量.则∑j相对于母坐标系∑i的齐次变换矩阵如下所示：

$_{j}^{i}T=\left[ \begin{matrix} {} & {{e}^{{{{\hat{a}}}_{j}}{{q}_{j}}}} & {} & {{b}_{j}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$    (4)

式中：“^”符号表示“帽子算法”，即把一个矢量变换为反对称的3阶方阵.

因此，只要定义了转动轴矢量为ai，相对位置矢量为bi和关节角度θi，就能求出齐次变换矩阵.至此，双足步行机器人运动学杆式模型建立完毕.Matlab软件中编制递归调用程序，只要给出10个关节的角度，就能生成机器人的一个位姿.图 1为用随机产生10个角度后的舞蹈机器人位姿图，从而验证了本文所建立的舞蹈机器人正运动学模型的正确性.

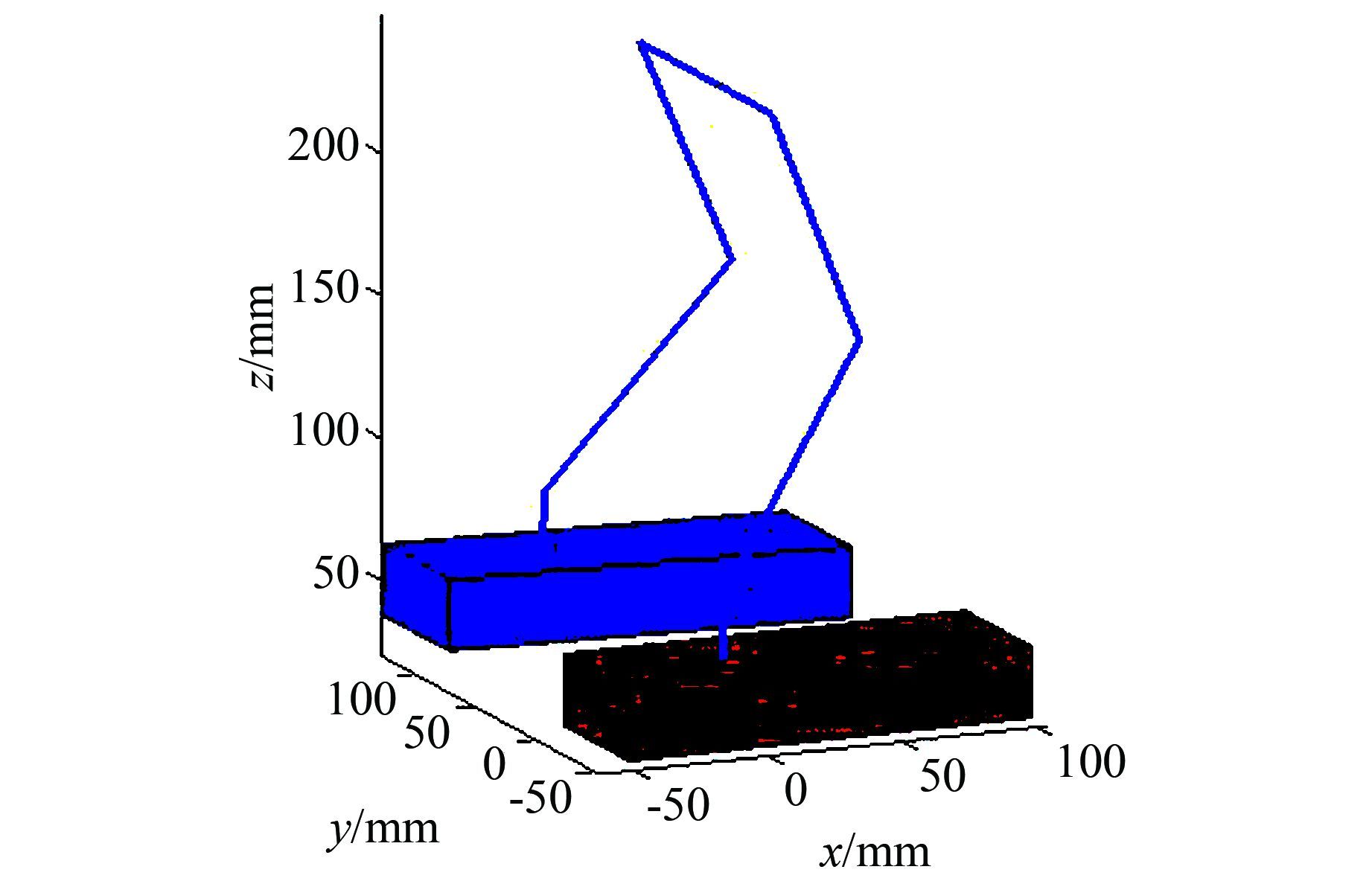
图 1 随机角度生成的模型位姿图 Figure 1 The robot pose by using random angle
图选项
1.2 逆运动学分析

通过机器人的上体和双腿末端的期望位姿，求解各个关节角度即为双足步行机器人的逆运动学分析.设定了双足机器人的动作，也即是给定了机器人确定的几何约束，机器人各关节的轨迹与姿态都是确定的.

求解运动学的方法可以分为解析解法和数值解法，逆运动学解析解精确，但通常需要大量的计算，而数值解法计算量小，且容易用于机器人的在线控制.本文使用数值解法.双足机器人的逆运动学的数值方法是给出一组初始角度值，通过正运动学得到足部坐标系的位姿矩阵，并计算误差，通过雅可比矩阵计算出关节角度的修正值，再进行下一次迭代.机器人的雅克比矩阵反映了操作空间和关节空间的映射关系.

假设机器人的末端执行器的空间位姿为

${\left[ {\begin{array}{*{20}{l}} {{p_i}}\\ {{\omega _i}} \end{array}} \right]_{6 \times 1}} = f\left( \theta \right)$    (5)

式中：ω为角速度矢量，ωi=ai×θi=(In${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over R} }$)，为前文帽子算法的逆运算；θ是从机器人首段到末端各个关节角组成的向量.两边求导得：

${\left[ \begin{array}{l} {{\dot p}_i}\\ {{\dot \omega }_i} \end{array} \right]_{6 \times 1}} = J\left( \theta \right)\dot \theta $    (6)

可见，在机器人的逆运动中，雅克比矩阵和牛顿迭代中的导函数，具有类似的意义.

雅克比矩阵的计算可写为下式：

$J = \left[ {\begin{array}{*{20}{c}} {J = _1^wa \times ({p_N} - {p_1})}&{_1^wa}\\ {a_2^wa \times ({p_N} - {p_2})}&{_2^wa}\\ \vdots & \vdots \\ {_{N - 1}^wa \times ({p_N} - {p_{N - 1}})}&{_{N - 1}^wa}\\ 0&{_N^wa} \end{array}} \right]_{N \times 6}^T$    (7)

其中：iwa为第i个关节在世界坐标系中的旋转轴矢量.

按照数值解法的流程编写逆运动学的程序，本文采用了Matlab提供的结构体定义各个连杆，结构体的域定义属于杆的属性，如Link(1).p表示杆1在世界坐标系中的位置矢量.调用运动学逆解的程序InverseKinematics(6，posRef)，得到舞蹈机器人的运动学图如图 2所示，验证了本文所建立的逆运动学模型的正确性.

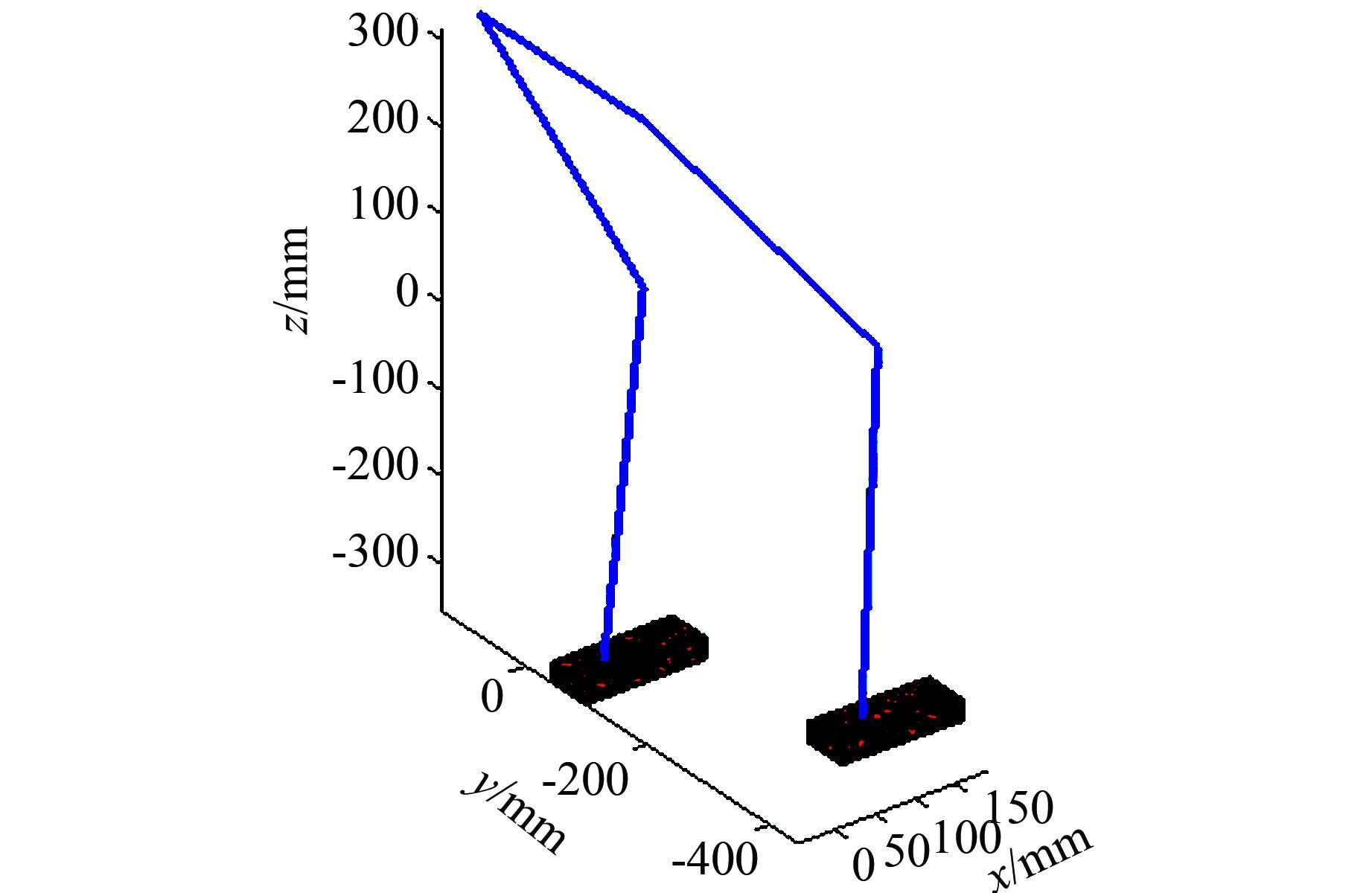
图 2 逆运动学求解结果 Figure 2 The robot pose by invert kinematics
图选项
2 ZMP稳定性分析

ZMP是指机器人步行过程中,支撑面内的一点,在这一点上作用在机器人的合力绕着这一点的力矩为 0 ,即机器人受到的地面反力中垂直分量对该点产生的合力矩为0[20].因此在舞蹈机器人步态规划中引入 ZMP作为稳定判据，进行舞蹈机器人步态规划.在oxz平面内，舞蹈机器人行走时转动角速度相对较小，忽略转动动能的影响，ZMP关于各个连杆的质心位置[xi,zi]和加速度[${{\ddot x}_i},{{\ddot z}_i}$]的表达式为

${x_{zmp}} = \frac{{\sum\limits_{i = 1}^n {} \left[ {{m_i}\left( {{{\ddot z}_i} + g} \right){x_i} - {m_i}\left( {{{\ddot x}_i} + g} \right){z_i}} \right]}}{{\sum\limits_{i = 1}^n {} {m_i}{{\left( {{{\ddot z}_i} + g} \right)}_i}}}$    (8)

将各连杆的质心位置和加速度与各关节的角度、角速度和角加速度的关系代入舞蹈机器人横纵坐标计算公式，可得ZMP的表达式如下：

$\begin{array}{l} {x_{zmp}} = \\ \frac{{\sum\limits_{i = 1}^n {} \left[ {{m_i}\left( {\frac{{\partial {z_i}}}{{\partial {\theta _i}}}{{\ddot \theta }_i} + \frac{{{\partial ^2}{z_i}}}{{\partial \theta _i^2}}\dot \theta _i^2 + g} \right){x_i} - {m_i}\left( {\frac{{\partial {x_i}}}{{\partial {\theta _i}}}{{\ddot \theta }_i} + \frac{{{\partial ^2}{x_i}}}{{\partial \theta _i^2}}\dot \theta _i^2} \right){z_i}} \right]}}{{\sum\limits_{i = 1}^n {} {m_i}\left( {\frac{{\partial {z_i}}}{{\partial {\theta _i}}}{{\ddot \theta }_i} + \frac{{{\partial ^2}{z_i}}}{{\partial \theta _i^2}}{{\dot \theta }^2}_i + g} \right)}} \end{array}$    (9)

机器人稳定运动的条件是包括惯性力在内的所有外力要平衡.需要满足以下运动条件：

1) 满足绕x轴和y轴的扭矩平衡，也就是舞蹈机器人绕x或y轴不产生翻转；

2) 地面摩擦力小于最大静摩擦力，确保行走时无滑动；

3) 满足绕z轴的扭矩平衡.

此外，舞蹈机器人绕z轴也不能出现滑转，因此还需要计算半径小于摩擦圆半径的条件.

3 步态参数定义

参考人类步行模式，舞蹈机器人的双足步行模式被分为如图 3所示的各个阶段.一个完整的步行周期由两个步行循环组成，每个循环包括一个单足相和一个双足相.舞蹈机器人采用交互式行走步伐，设定机器人先抬左腿，将机器人向前运动过程分为下蹲、左脚向前、右脚向前，然后多次循环，前进运动结束后起立，动作停止.

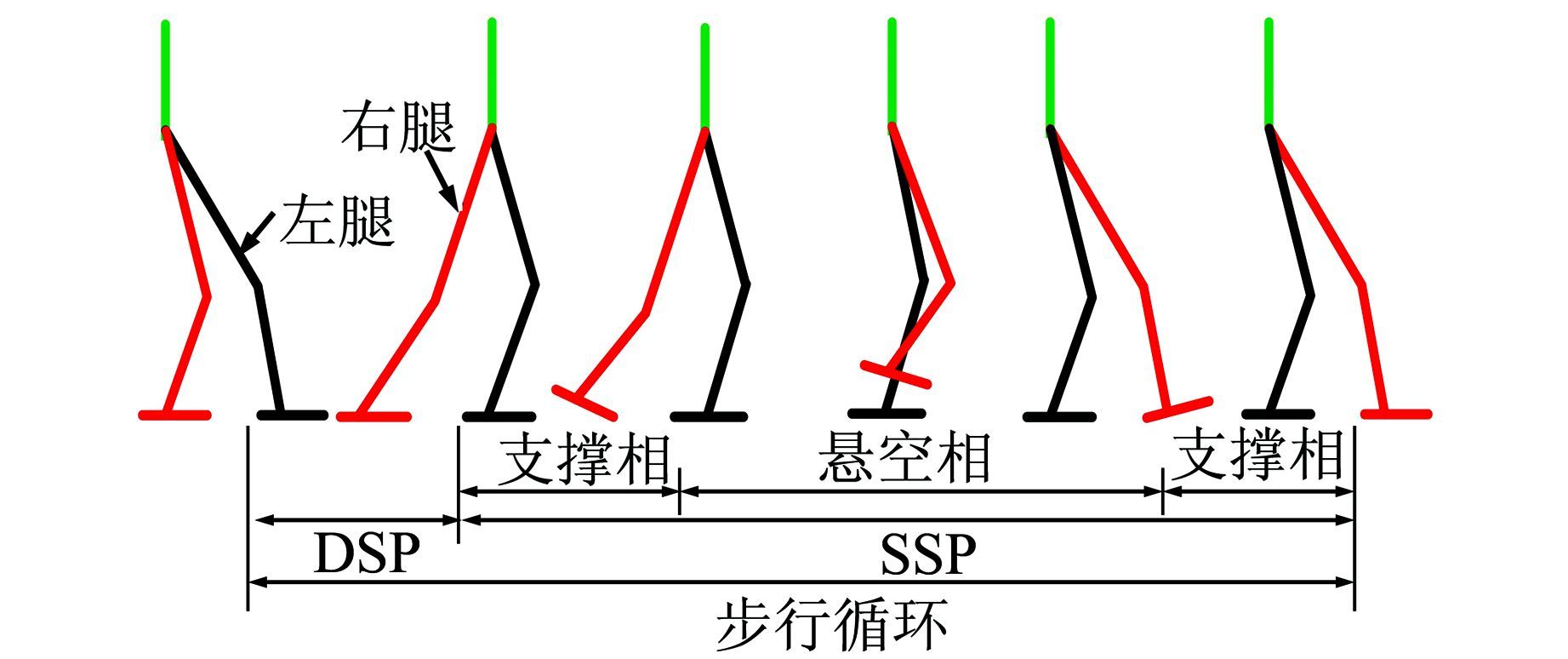
图 3 双足步态阶段 Figure 3 Phases of biped gait
图选项

舞蹈机器人行走的主要参数包括步长L、步宽W、足底平面抬起时和地面的最大夹角θ1、足底平面落地时和地面的最大夹角θ2.本文中的WS参数设置如下：T1= T2=0.05s，单足相时间TS=0.7 s，双足相时间TD=0.3 s，步长L=0.04 m，步宽W=0.1 m，θ1=θ2=2°.

4 基于三维线性倒立摆的步态规划

为实现舞蹈机器人期望的步行方式，就要通过一定的方法得出一组关节角时间序列，此过程称之为舞蹈机器人步态规划.常用的步态规划方法包括强制学习法、参考轨迹法、自然动力学法等.舞蹈机器人在步态上需要更加接近人类的形态，而三维线性倒立摆的步态规划方法可以实现类人行走的步态，因此本文采用该方法进行步态规划.

4.1 ZMP轨迹和质心轨迹生成

根据三维线性倒立摆模型[21]，在单足相期间，可以得到如下方程：

$\left\{ \begin{array}{l} \ddot x = {\omega ^2}\left( {x - {p_x}} \right)\\ \ddot y = {\omega ^2}\left( {x - {p_y}} \right)\\ \omega = \sqrt {g/{Z_c}} \end{array} \right.$    (10)

式中：Zc为ZMP高度.以rcom=[x,y,z]T代表质心COM的位置，p=[px,py,pz]T代表ZMP的位置.

通过规划好的ZMP轨迹求解机器人的质心轨迹，求解这个方程目前比较有效的方法是离散化的方法，其过程可归纳如下：

设采样时间Δt，则加速度可以近似为

$p = x - \frac{{{z_c}}}{g}\ddot x$    (11)

其中：xi表示第i个采样时刻的质心在x方向的位移.则式(11)化为

${p_i} = a{x_{i - 1}} + b{x_i} + c{x_{i + 1}}$    (12)

其中：

$\left\{ \begin{array}{l} {a_i} = - {Z_c}/\left( {g\Delta {t^2}} \right)\\ {b_i} = 2{Z_c}/(g\Delta {t^2}) + 1\\ {c_i} = - {z_c}/\left( {g\Delta {t^2}} \right) \end{array} \right.$    (13)

写成矩阵的形式，可得

$p = Ax$

其中：

$\begin{array}{l} p = {\left[ {\begin{array}{*{20}{c}} {{p_1}}&{{p_2}}& \cdots &{{p_{N - 1}}}&{{p_N}} \end{array}} \right]^T}\\ x = {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_{N - 1}}}&{{x_N}} \end{array}} \right]^T}\\ A = \left[ {\begin{array}{*{20}{c}} {{a_1} + {b_1}}&{{c_1}}&0&0&0&0&0\\ {{a_2}}&{{b_1}}&{{c_2}}& \ddots &0&0&0\\ 0&0&0& \ddots &0&0&0\\ 0&0&0& \ddots &{{a_{N - 1}}}&{{b_{N - 1}}}&{{c_{N - 1}}}\\ 0&0&0&0&0&{{a_N}}&{{b_N} + {c_N}} \end{array}} \right] \end{array}$

逆解为x=A-1p.假设杆式模型的实际ZMP轨迹是p*，则质心的修正量：

$\Delta x = {A^{ - 1}}\left( {{p^{ref}} - {p^*}} \right)$    (14)

这样可以通过几次循环，使ZMP的误差减小，实际上，这样就能够在一定程度上减小把机器人简化为一个质点所带来的误差.根据上述算法，结合文中采用的WS参数，最终生成的ZMP轨迹如图 4所示，(a)图为质心轨迹和ZMP轨迹在x方向的对比，(b)图为在y方向的对比.从图中可以发现本文方法的实际ZMP 较好地跟踪了期望ZMP，从而确保舞蹈机器人在行走过程中的稳定性.从图中可以发现x方向和y方向输出ZMP在步行初始时刻有一个阶梯状跳变，这是由于在此时期望ZMP设定在脚掌中心位置，而给定舞蹈机器人状态则是直立静止，因此ZMP落在重心投影点与脚掌中心之间存在偏差，本文所采用的迅速跟踪期望ZMP的算法导致了如图所示的跳变.

图 4 规划ZMP轨迹与质心轨迹 Figure 4 ZMP and centroid trajectories
图选项
4.2 足部轨迹插值

为了追求更高的步行效率，应该考虑单足相时游脚踝关节转动自由度.生成足部轨迹之后，踝关节位置可以计算出来，然后可以通过踝关节位姿和躯干位姿利用逆运动学解算得到连杆的关节角度.踝关节运动包括踝关节的位置wxankd和姿态wRankd.踝关节的位置和姿态可以表示为

$\left\{ \begin{array}{l} ^wx_{ank}^d{ = ^w}x_c^d{ + ^c}x_r^d{ + ^c}R_r^d \times {x_{r - ank}}\\ ^wR_{ank}^d{ = ^c}R_r^d \end{array} \right.$    (15)

其中：wxcd是在世界坐标系的支撑脚位置矢量；cxrd是定义在支撑脚坐标系的游脚位置矢量；cRrd是游脚与支撑脚坐标系相关的姿态矩阵.

根据步态参数，采用3次埃尔米特插值得到cxrd和θ轨迹.在Matlab中编写脚步插值函数，根据本文所设置的步态参数运行得到足部轨迹如图 5所示.

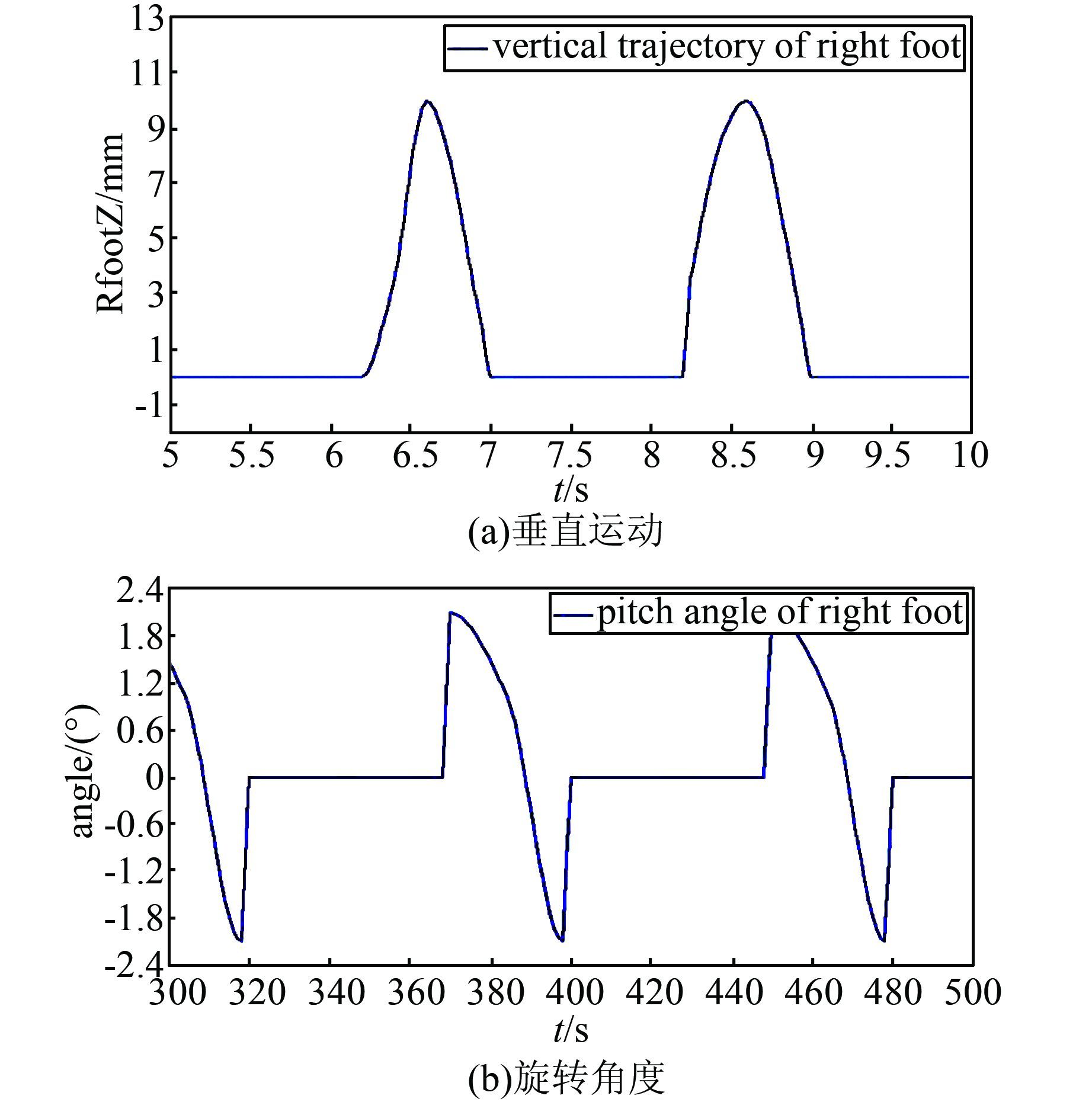
图 5 右足垂直运动和旋转角度轨迹 Figure 5 Vertical motion and helix angle of right foot
图选项
4.3 舞蹈机器人步态规划

在步态规划时，先给出舞蹈机器人的WS参数，然后计算舞蹈机器人落脚点位置和足部轨迹，再计算质心轨迹，然后利用舞蹈机器人逆运动学求解得到各个关节的角度值，即可完成基本的步态规划.舞蹈机器人的步态规划流程图如图 6所示.

图 6 舞蹈机器人步态规划流程图 Figure 6 Flow chart for biped robot gait planning
图选项
5 仿真结果与实验验证

在Matlab中编程实现上述过程，取单足相时间为0.7s,双足相时间为0.3 s.完成上述过程后，通过Matlab生成步态模式，因为左右对称，以右腿为例，各个关节的角度随时间变化的曲线如图 7所示.由图 7可知各角度轨迹变化都很平滑.由于舞蹈机器人步行时躯干下蹲，膝关节前曲，同时保持髋关节高度不变，所以膝关节的角度较大，且都为正值，最大值约为1.2 rad.而由于机器人的步长相对于腿长而言较小，因此机器人的髋关节和踝关节俯仰角度(Pitch Angle)均为负值，且最大值约为0.7 rad.同时，滚动角(Roll Angle)幅值变化也较小，大约为0.2~0.3 rad，且均为正值.

图 7 离线步态模式 Figure 7 Off-line gait mode
图选项
6 结论

本文首先建立双足舞蹈机器人的运动学模型，并对其进行正逆运动学分析，求解机器人各关节；引入三维倒立摆模型，结合ZMP稳定性理论建立了舞蹈机器人步态规划算法；结合本文所提出的步态参数设置，对舞蹈机器人的行走步态进行了仿真计算，通过正逆运动学仿真计算得到各个关节角度与角速度的时程曲线.上述结果可作为物理样机各关节的理想输入，从而实现舞蹈机器人的动作控制.

参考文献
[1] 蔡自兴. 机器人学[M]. 北京: 清华大学出版社, 2000.
Cai Zixing. Robotics[M]. Beijing: Tsinghua University Press, 2000.
[2] 程南瑞, 刘国栋, 徐菊香. 基于实时ZMP检测的类人足球机器人步态规划[J]. 计算机仿真, 2010(4): 154–158.
Chengs Nanrui, Liu Guodong, Xu Juxiang. Gait planning of humanoid soccer robot based on real-time ZMP measurement[J]. Computer Simulation, 2010(4): 154–158.
[3] 唐策, 赵现朝, 齐臣坤. 人形机器人建模与步态规划[J]. 机械制造与自动化, 2012(4): 158–162.
Tang Ce, Zhao Xianchao, Qi Chengkun. Humanoid robot simulation and gait planning[J]. Jiangsu Machine Building & Automation, 2012(4): 158–162.
[4] 阮鹏, 俞志伟, 张昊, 等. 基于ADAMS的仿壁虎机器人步态规划及仿真[J]. 机器人, 2010, 32(4): 499–504.
Ruan Peng, Yu Zhiwei, Zhang Hao. Gait planning and simulation of gecko inspired robot based on ADAMS[J]. Robot, 2010, 32(4): 499–504. DOI:10.3724/SP.J.1218.2010.00499
[5] 郑万通, 仉俊峰, 王东, 等. 仿人机器人舞蹈动作的研究[J]. 自动化技术与应用, 2015, 10: 134–137.
Zheng Wantong, Zhang Junfeng, Wang Dong, et al. Study of humanoid robot’s dancing action[J]. Techniques of Automation and Applications, 2015, 10: 134–137.
[6] Ogura Y, Aikawa H, Shimomura K, et al. Development of a new humanoid robot WABIAN-2[C]// Proceedings of 2006 IEEE International Conference on Robotics and Automation. IEEE, 2006: 76-81.
[7] Ishida T. Development of a small biped entertainment robot QRIO [C]// International Symposium on Micro-Nanomechatronics and Human Science. Nagoya, Japan, 2004: 23-28.
[8] Sakagami Y, Watanabe R, Aoyama C, et al.The Intelligent ASIMO: System overview and integration[C]// International Conference on Intelligent Robots and Systems. EPFL, Lausanne, Switzerland, 2002: 2478-2483.
[9] Akachi K, Kaneko K, Kanehira N, et al.Development of humanoid robot HRP-3P [C]// IEEE-RASI International Conference on Humanoid Robots, Tsukuba, Japan: 50-55.
[10] Srinivasan M, Ruina A. Computer optimization of a minimal biped model[J]. Nature, 2006, 439: 72–75. DOI:10.1038/nature04113
[11] Boston Dynamics . http://www.bostondynamics.com/robot_bigdog.html.
[12] Boston Dynamics . http://www.bostondynamics.com/robot_petman.html.
[13] Boston Dynamics . http://www.bostondynamics.com/robot_Atlas.html.
[14] 董金波. 双足机器人步态规划与运动学仿真研究[J]. 机械与电子, 2011(07): 66–69.
Dong Jinbo. Research of gait planning and kinematics simulation for Biped Robot[J]. Machinery & Electronics, 2011(07): 66–69.
[15] 梁青, 宋宪玺, 周烽, 等. 基于ADAMS的双足机器人建模与仿真[J]. 计算机仿真, 2010(5): 162–165.
Liang Qing, Song Xianxi, Zhou Feng, et al. Modeling and simulation of biped robot based on ADAMS[J]. Computer Simulation, 2010(5): 162–165.
[16] 杜志江, 张博, 孙立宁, 等. 基于虚拟样机技术的双足机器人运动仿真研究[J]. 系统仿真学报, 2007, 19: 4454–4456.
Du Zhijiang, Zhang Bo, Sun Lining. Research on motion simulation of biped walking robot based on virtual prototype technology[J]. Journal of System Simulation, 2007, 19: 4454–4456.
[17] 王立权, 俞志伟. 基于ADAMS的双足机器人拟人行走动态仿真[J]. 计算机仿真, 2009(3): 160–164.
Wang Liquan, Yu Zhiwei. Dynamic simulation of biped robot human-like walking based on ADAMS[J]. Computer Simulation, 2009(3): 160–164.
[18] 吴泽琦, 吴根忠. 基于遗传算法优化的仿人足球机器人步态规划研究[J]. 机电工程, 2012(11): 1340–1344.
Wu Zeqi, Wu Genzhong. Research of humanoid soccer robot gait planning based on GA optimized[J]. Mechanical & Electrical Engineering Magazine, 2012(11): 1340–1344.
[19] 张勇, 许东来. 小型双足步行机器人的步态规划[J]. 计算机仿真, 2010(11): 148–151.
Zhang Yong, Xu Donglai. Small biped robot walking gait planning[J]. Computer Simulation, 2010(11): 148–151.
[20] 窦瑞军, 马培荪. 基于ZMP点的两足机器人步态优化[J]. 机械科学与技术, 2003, 22(1): 77–79.
Dou Ruijun, Ma Peisun. ZMP-based gait optimization of a biped robot[J]. Mechanical Science and Technology, 2003, 22(1): 77–79.
[21] 于国晨, 刘永信, 李晓红. 基于三维线性倒立摆的仿人机器人步态规划[J]. 计算机应用, 2012(9): 2643–2647.
Yu Guochen, Liu Yongxin, Li Xiaohong. Humanoid robot gait planning based on 3D linear inverted pendulum model[J]. Journal of Computer Applications, 2012(9): 2643–2647.