武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 806-811

文章信息

张湾, 李典庆, 曹子君
ZHANG Wan, LI Dianqing, CAO Zijun
基坑开挖参数反分析贝叶斯方法比较研究
Comparative study of Bayesian methods for back analysis of deep excavation
武汉大学学报(工学版), 2016, 49(6): 806-811
Engineering Journal of Wuhan University, 2016, 49(6): 806-811
http://dx.doi.org/10.14188/j.1671-8844.2016-06-002

文章历史

收稿日期: 2016-05-18
 Abstract              PDF               Figures               Tables
引用本文 0
张湾, 李典庆, 曹子君. 基坑开挖参数反分析贝叶斯方法比较研究[J]. 武汉大学学报(工学版), 2016, 49(6): 806-811.
ZHANG Wan, LI Dianqing, CAO Zijun. Comparative study of Bayesian methods for back analysis of deep excavation[J]. Engineering Journal of Wuhan University, 2016, 49(6): 806-811.
基坑开挖参数反分析贝叶斯方法比较研究
张湾, 李典庆, 曹子君     
武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072
收稿日期: 2016-05-18
作者简介: 张湾(1990-)，女，硕士研究生，主要从事岩土工程不确定性分析方面的研究，E-mail：wanzhang@whu.edu.cn.
通讯作者: 曹子君(1987-)，男， 副教授，主要从事岩土工程不确定性分析与风险评价方面的研究，E-mail：zijuncao@whu.edu.cn
基金项目: 国家杰出青年基金项目(编号：51225903)；国家自然科学基金项目(编号：51409196，51579190，51528901).
摘要: 根据基坑开挖过程中获取的现场监测数据可以反分析现场土层的土体参数.贝叶斯方法为充分利用现场监测数据分析土体参数提供了一条有效的途径.实现贝叶斯更新一般有两种方法：一是各开挖阶段的观测值依次对土体参数进行更新，即分步更新，更新过程中需假设后验分布类型，如正态分布；二是将多阶段的观测值作为整体对土体参数进行更新，即整体更新.为了研究贝叶斯更新方法对更新结果的影响，在先验分布为正态或均匀分布时分别采用这两种方法对台北国营企业中心开挖工程的土体参数进行更新.结果表明：当先验分布为正态分布时，假设后验分布为正态分布进行分步更新，得到的参数分布基本合理，能够准确预测开挖引起的最大沉降和失效概率；相反，当先验分布为均匀分布时，假设后验分布为正态分布进行分步更新，不能够准确预测开挖引起的最大沉降和失效概率，此时应采用整体更新方法.
关键词： 贝叶斯方法     分步更新     整体更新     先验分布    
Comparative study of Bayesian methods for back analysis of deep excavation
ZHANG Wan, LI Dianqing, CAO Zijun     
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China
Abstract: In the process of excavation, the field observation data can be obtained constantly, which can be used to update the soil parameters using Bayes’ theorem. There are two common ways to update the soil parameters using field observation data: multiple observation data are used in the Bayesian framework in a sequential manner, or as a whole. It needs to make assumptions on the type of posterior distribution (e.g., normal) in the updating process when using multiple observation data in a sequential manner. In order to study the effect of the Bayesian updating methods, the two methods are, respectively, used to the Taipei National Enterprise Center case when the prior distribution is normal or uniform. It is found that, for normal prior distribution, the normal posterior distribution characterizes soil parameters reasonably, leading to proper estimation of maximum ground settlement and failure probability. On the other hand, for uniform prior distribution, assuming normal posterior distribution in Bayesian sequential updating may result in overestimation of maximum ground settlement and failure probability. In such a case, it is prudent to use all the observation data as a whole to update the soil parameters in one step.
Key words: Bayesian methods     sequential updating     one-step updating     prior distribution    

在基坑开挖过程中，不可避免地会引起周围地表的沉降，如果这种地表沉降超过允许值，将会对邻近建筑物造成严重的破坏[1].为了避免这种破坏的发生，可以在开挖前对可能引起的最大地表沉降进行预测，制定对应的工程措施[2].然而，要对响应进行准确的预测，需要知道土体参数的准确分布.而实际上，对于某一特定位置土体参数的分布，现有的认识是有限的.但开挖通常是分阶段进行的，可以根据开挖过程中获取的监测数据对土体参数进行反分析.比如，当上一个开挖阶段结束后，现场监测到的最大地表沉降可用于进行土体参数的更新，在得到更新后的土体参数后就可以对后面开挖阶段的响应进行更准确的预测.

文献中现有的土体参数的反分析方法包括最小二乘法[3]、单纯形法[4]、贝叶斯方法[5].其中，贝叶斯方法是一个更新输入参数的稳健方法[6].现有学者基于贝叶斯方法对基坑开挖问题进行更新时，多采用分步更新的方法[1-2, 7]，即以各开挖阶段的观测值依次对土体参数进行更新，在更新过程中将上一步更新得到的后验分布作为下一步更新的先验分布[7]，而后验分布一般通过马尔科夫链蒙特卡洛模拟(Markov Chain Monte Carlo simulation，MCMCS)[2, 5, 8]产生的样本分析得到.由于MCMCS只能得到后验分布的样本，要得到后验分布，就需要对其类型作出一定的假设，通常假设其为正态分布[2, 7].但是，这种假设对土体参数更新结果的影响是未知的.理论上，后验分布类型假设对更新结果的影响与先验分布有关.为了研究先验分布及后验分布类型对土体参数更新结果的影响，本文采用整体更新的方法[7, 9]进行计算，即将开挖多阶段的观测值作为整体对土体参数进行更新，并以此为标准，评估分步更新中后验分布假设的影响.本文在先验分布为正态或均匀时，分别采用分步更新和整体更新的方法对台北国营企业中心(Taipei National Enterprise Center, TNEC)基坑开挖工程的土体参数进行了贝叶斯更新.贝叶斯更新过程中采用Kung-Juang-Hsiao-Hashash(KJHH)模型[10-11]计算最大地表沉降，根据更新后的土体参数预测后面开挖阶段的最大地表沉降和失效概率.在此基础上，探讨了先验分布和不同贝叶斯更新方法对最大地表沉降和失效概率的影响.

1 基于贝叶斯理论的反分析方法

在开挖问题中，可以利用一些理论或经验模型对响应进行预测，令δ(θ)代表响应y的模型预测值，其中θ表示待更新土体参数构成的向量.由于任何模型都只是对实际的一种近似或简化，模型不确定性总是存在的，令c代表模型偏差系数，则考虑模型不确定性的预测响应表达为

$y=c\delta (\mathbf{\theta })$    (1)

式中: δ(θ)可以通过KJHH模型计算.随着开挖的进行，观测数据不断增加，可采用两种贝叶斯方法对土体参数进行更新.第一种是以各阶段的观测值依次对土体参数进行更新，即分步更新；第二种是将多阶段的观测值作为整体对土体参数进行更新，即整体更新.

1.1 分步更新

当以各阶段的观测值依次对土体参数进行更新时，上一步贝叶斯更新得到的土体参数θ的后验分布可以作为下一步更新的先验分布.比如，利用第i-1次更新的现场观测值yobs(i-1) 对土体参数θ进行更新，得到的后验分布为p(θ|yobs(i-1) )，将它作为第i次更新的先验分布，则第i次更新的后验分布为

$p(\mathbf{\theta }|{{y}_{obs\text{i}}})={{m}_{1}}f({{y}_{obs\text{i}}}\text{ }\!\!|\!\!\text{ }\mathbf{\theta })p(\mathbf{\theta }|{{y}_{obs(i-1)}})$    (2)

式中: m1为归一化常数；yobsi为第i次更新的现场观测值；f(yobsi|θ)为似然函数.本文利用c=yobsi/δ(θ)的分布计算似然函数，即f(yobsi|θ)=f(yobsi/δ(θ)).采用MCMCS根据式(2) 产生大量的θ样本.假设后验分布为联合正态分布[2, 7]，根据θ的样本可以确定后验分布，并将其作为第i+1步更新的先验分布.本文基于Metropolis-Hastings算法执行MCMCS，由于篇幅限制，不对其算法展开介绍，具体算法请参阅文献[2, 5, 8].分步更新方法在每次更新过程中，只考虑一个现场观测值，对于每个MCMCS样本只需要计算一次系统响应，与整体更新相比计算量较小.但是，由于这种方法假设了后验分布类型，可能引入一定的误差，更新结果的有效性无法保证.

1.2 整体更新

当多阶段的现场观测值(yobs1, yobs2, …, yobsi)作为整体对土体参数进行更新时，假设在给定土体参数的条件下每个阶段的观测值是相互独立的，则根据前i阶段观测值更新土体参数θ的后验分布为[7]

$p(\mathbf{\theta }\text{ }\!\!|\!\!\text{ }{{y}_{obs1}},{{y}_{obs2}},...,{{y}_{obsi}})={{m}_{2}}\prod\limits_{j=1}^{i}{f({{y}_{obsj}}\text{ }\!\!|\!\!\text{ }\mathbf{\theta })}p(\mathbf{\theta })$    (3)

式中: m2为归一化常数；p(θ)为θ的先验分布，在整体更新过程中，各更新阶段始终保持不变.f(yobsj|θ)为每个观测值对应的似然函数值，可通过c=yobsj/δ(θ)的分布计算，即f(yobsj|θ)=f(yobsj/δ(θ)).为了提高整体更新的准确性，本文采用数值积分计算公式(3) 中的后验分布.虽然将多阶段的现场观测值作为整体对土体参数进行更新的过程避免了假设后验分布的类型，但是随着开挖的进行，现场数据不断增加，求解贝叶斯方程的计算量也会不断增加.为了降低求解计算量，本文采用KJHH模型计算基坑开挖引起的最大地表沉降.

2 KJHH模型

KJHH模型是个半经验模型[10]，可以用来预测软黏土中支撑开挖的挡土墙最大侧向位移δhm、变形率R(R=δvm/δhm)和地表沉降.

在基坑开挖问题中，其他经验或半经验方法也可以用来估计开挖引起的最大地表沉降，但是这些方法没有很好地建立挡土墙侧向位移和地表沉降的联系，并且不能量化不确定性[10]，因此本文采用KJHH模型进行计算.

根据KJHH模型，挡土墙最大侧向位移δhm预测为[10]

$\begin{align} & {{\delta }_{hm}}(mm)={{a}_{0}}+{{a}_{1}}{{X}_{1}}+{{a}_{2}}{{X}_{2}}+{{a}_{3}}{{X}_{3}}+{{a}_{4}}{{X}_{4}}+{{a}_{5}}{{X}_{5}}+ \\ & {{a}_{6}}{{X}_{1}}{{X}_{2}}+{{a}_{7}}{{X}_{1}}{{X}_{3}}+{{a}_{8}}{{X}_{1}}{{X}_{5}} \\ \end{align}$    (4)

式中: X1=t(He)，He为开挖深度；X2=t[ln(EI/γwhhavg4)]，E为挡土墙的杨氏模量，I为墙体截面的惯性矩，γw为水的单位重度，hhavg为支撑的平均间隔；X3=t(B/2) ，B为开挖宽度；X4=t(Su/σ′v)，Su为不排水抗剪强度，σ′v为垂直有效应力；X5=t(Ei/σ′v)，Ei为初始杨氏模量.公式(4) 中的系数由最小二乘法得到为: a0=-13.419 73，a1=-0.493 51，a2=-0.098 72，a3=0.060 25，a4=0.237 66，a5=-0.154 06，a6=0.000 93，a7=0.002 85，a8=0.001 98.变量Xi(i=1, 2，…, 5) 是5个输入参数的转换变量[10]:

${{X}_{i}}=t({{x}_{i}})={{b}_{1}}x_{i}^{2}+{{b}_{2}}{{x}_{i}}+{{b}_{3}}$    (5)

式中: xi(i=1, 2，…, 5) 是相应的输入参数，系数由误差最小原则确定，见表 1.

表 1 输入变量线性转换系数[10] Table 1 Coefficients for linear transformation of input variables
变量(x)b1b2b3
He-0.424-50
ln(EI/γwhavg4)11.5-2952 000
B/2-0.04490
Su/σ′v3 225-2 882730
Ei/σ′v0.000 41-1500
表选项

根据KJHH模型，变形率R(即最大地表沉降δvm与挡土墙最大侧向位移δhm的比值)为[10]

$\begin{align} & R={{c}_{0}}+{{c}_{1}}{{Y}_{1}}+{{c}_{2}}{{Y}_{2}}+{{c}_{3}}{{Y}_{3}}+{{c}_{4}}{{Y}_{1}}{{Y}_{2}}+{{c}_{5}}{{Y}_{1}}{{Y}_{3}}+{{c}_{6}}{{Y}_{2}}{{Y}_{3}}+ \\ & {{c}_{7}}Y_{3}^{3}+{{c}_{8}}{{Y}_{1}}{{Y}_{2}}{{Y}_{3}} \\ \end{align}$    (6)

式中: Y1=∑Hclay/Hwall，∑Hclay为挡土墙深度范围内所有黏土层的厚度，Hwall为挡土墙的长度；Y2=Su/σ′v；Y3=Ei/1000σ′v.公式(6) 中系数由最小二乘法得到为: c0=4.556 22，c1=-3.401 51，c2=-7.376 97，c3=-4.994 07，c4=7.141 06，c5=4.600 55，c6=8.748 63，c7=0.380 92，c8=-10.589 58.

最终，最大地表沉降δvm为

${{\delta }_{vm}}=R{{\delta }_{hm}}$    (7)

已知预测最大地表沉降δvm的模型偏差系数c服从均值为1.0、标准差为0.34的正态分布[10].本文中采用该分布计算式(2) 和(3) 中的似然函数.公式(4) 和(6) 的系数是根据大量开挖算例由最小二乘法得到的，将KJHH模型应用于新的开挖算例时，一般不考虑系数的改变，而是用模型偏差系数进行修正.当KJHH模型应用于不同的开挖算例时，模型偏差系数的分布应该不同.因此，在更新土体参数的同时模型偏差系数也应该得到更新，这将在以后的研究中进行探讨.

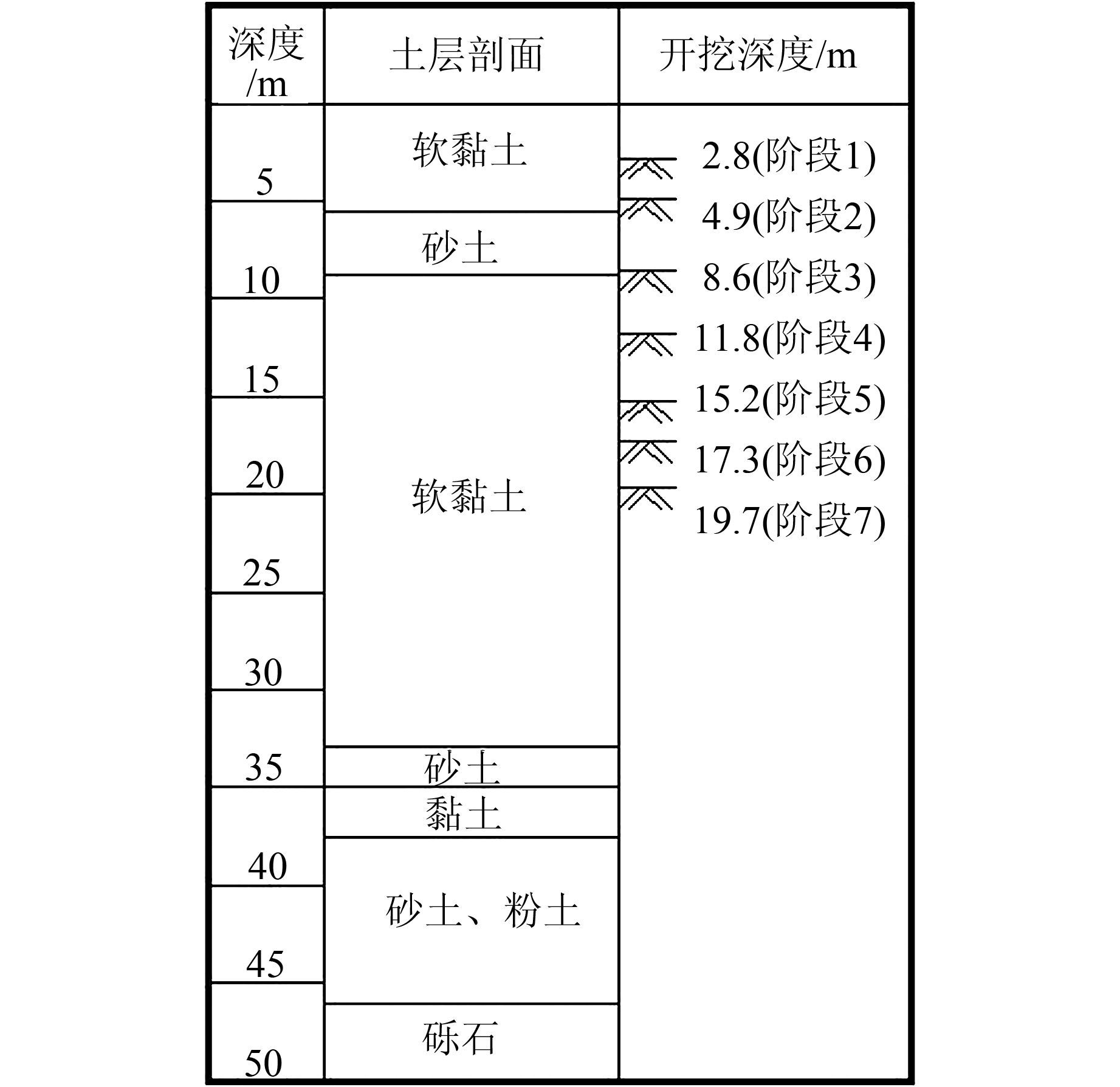
3 TNEC基坑开挖

本文以一个资料完备的开挖工程TNEC[12]为例说明不同先验分布下两种更新方法对土体参数贝叶斯更新结果的影响.TNEC位于台北，土层剖面见图 1.开挖宽度B=41.2 m，挡土墙厚度t=0.9 m，长度Hwall=35 m.采用明挖法，分7个阶段进行开挖.由于开挖的前两个阶段地表沉降比较小，用这两个阶段的地表沉降观测值进行土体参数的更新效果不显著[2].因此，本文从第3个开挖阶段进行贝叶斯更新.各开挖阶段的开挖深度、系统刚度和最大地表沉降观测值见表 2.黏土名义厚度∑Hclay/Hwall=0.87，硬土层位于地面以下46 m处，可以忽略其影响[10].由于最大地表沉降主要受土体名义不排水抗剪强度(Su/σ′v)和名义初始杨氏模量(Ei/σ′v)的影响[1-2]，所以本文利用现场观测值，使用贝叶斯理论对这两个土体参数进行更新，即θ={Su/σ′v和Ei/σ′v}.

图 1 TNEC土层剖面[2] Figure 1 Soil profile of the TNEC case
图选项
表 2 TNEC各阶段开挖深度、系统刚度和最大地表沉降观测值[1-2] Table 2 Mean values of excavation depths, system stiffnesses and observed maximum ground settlements of TNEC
因素开挖阶段
34567
开挖深度/m8.6011.8015.2017.3019.70
系统刚度1 0239661 1091 1151 294
最大地表沉降观测值/mm17.7233.8151.8666.6377.79
表选项

更新过程如下: 首先对先验分布作假设，为了研究先验分布对贝叶斯更新的影响，分别采用表 3中的先验分布进行计算.当第3个阶段开挖结束后，深度为8.60 m处的最大地表沉降观测值为17.72 mm，利用这个观测值和第1部分的贝叶斯更新方程，分别采用分步更新和整体更新的方法对土体参数Su/σ′v、Ei/σ′v进行贝叶斯更新.对于分步更新方法，假设后验分布为正态分布，根据贝叶斯方程(式(2) )采用基于Metropolis-Hastings算法的MCMCS得到后验分布的样本，并求得样本的均值、标准差和相关系数，最终可以得到后验分布的显式表达式.这时可以利用更新后土体参数的均值预测第4、5、6、7阶段的最大地表沉降，并取0.5%He作为开挖各阶段的极限地表沉降[9]，求出4、5、6、7阶段失效概率的预测值.对于整体更新方法，采用数值积分的方法求解贝叶斯方程(式(3) )，同样可以求出4、5、6、7阶段的最大地表沉降和失效概率(即P(δvm>0.5%He))的预测值.

当第4个阶段开挖结束后，观测到深度为11.80 m处的最大地表沉降为33.81 mm.对于分步更新方法，第3阶段更新得到的后验分布可以作为第4个阶段更新的先验分布，仍采用基于Metropolis-Hastings算法的MCMCS进行求解，并对5、6、7阶段的最大地表沉降和失效概率进行预测.对于整体更新方法，先验分布仍为表 3中的先验分布，似然函数为3、4阶段似然函数累乘，得到贝叶斯方程后采用数值积分的方法进行求解，并对5、6、7阶段的最大地表沉降和失效概率进行预测.重复上述计算过程直到开挖结束.

表 3 先验分布 Table 3 Prior distributions
土体参数正态分布均匀分布
均值变异系数下限上限
Su/σ′v0.250.160.20.4
Ei/σ′v5000.162001 200
注: 正态分布的统计特征来自参考文献[1-2, 9]；对于均匀分布，统计特征为上下界限, 取为KJHH的适用范围[10].
表选项
3.1 分步更新结果

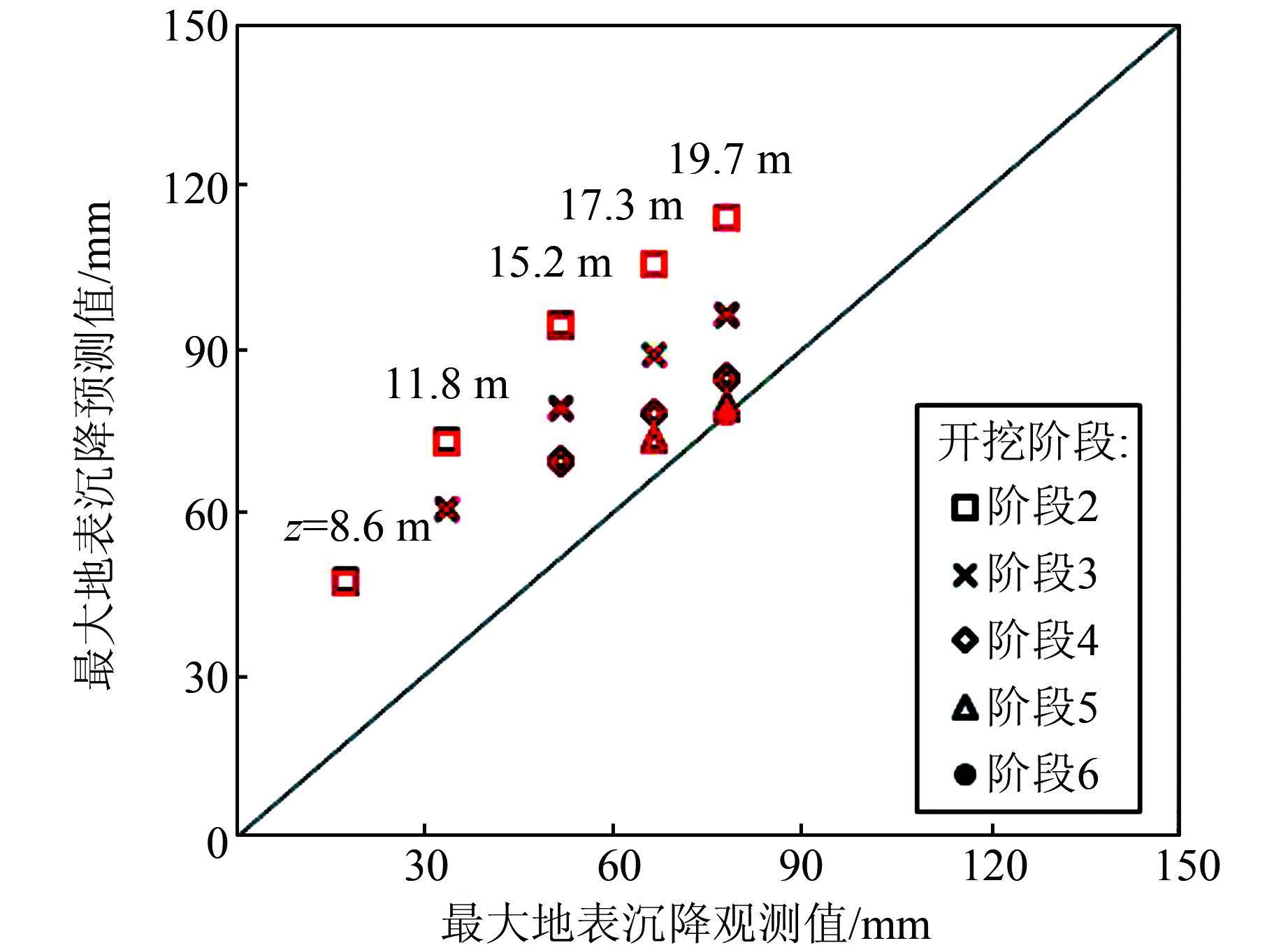
先验分布为正态分布时，分步更新方法各阶段最大地表沉降预测值见图 2，此时的计算过程与文献[2]相同，为了比较，将文献[2]的结果也画在了图 2上.由此可以看出，在先验分布为正态分布的条件下，分步更新方法的计算结果与文献[2]的结果是一致的(黑色与红色很接近)，验证了本文模型的正确性.

图 2 正态先验分布下分步更新最大地表沉降预测值(黑色表示本文结果；红色表示文献[2]结果) Figure 2 Predicted maximum ground settlements under normal prior distribution using Bayesian method in a sequential manner
图选项

为了研究先验分布对更新结果的影响，分别采用正态分布和均匀分布作为先验进行分步更新，预测的最大地表沉降见图 3.如图 3所示，不同先验分布导致了最大地表沉降预测值的显著差异.造成这种差异的原因主要是当先验分布为均匀分布时，参数后验分布受到显著影响，进而影响了最大地表沉降的预测值.

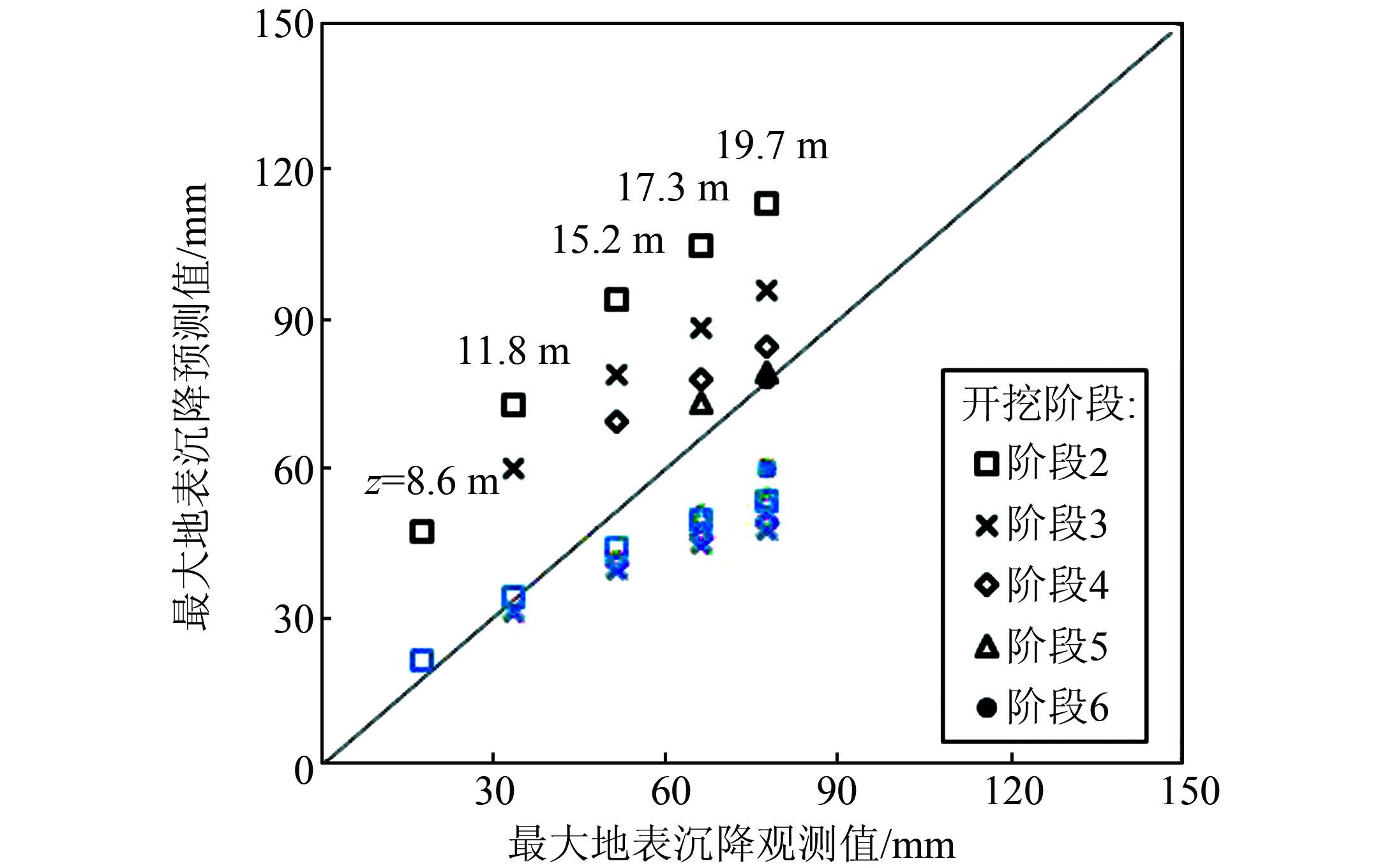
图 3 不同先验分布下分步更新最大地表沉降预测值(黑色表示正态分布对应的结果；蓝色表示均匀分布对应的结果) Figure 3 Predicted maximum ground settlements under different prior distributions using Bayesian method in a sequential manner
图选项
3.2 更新方法比较

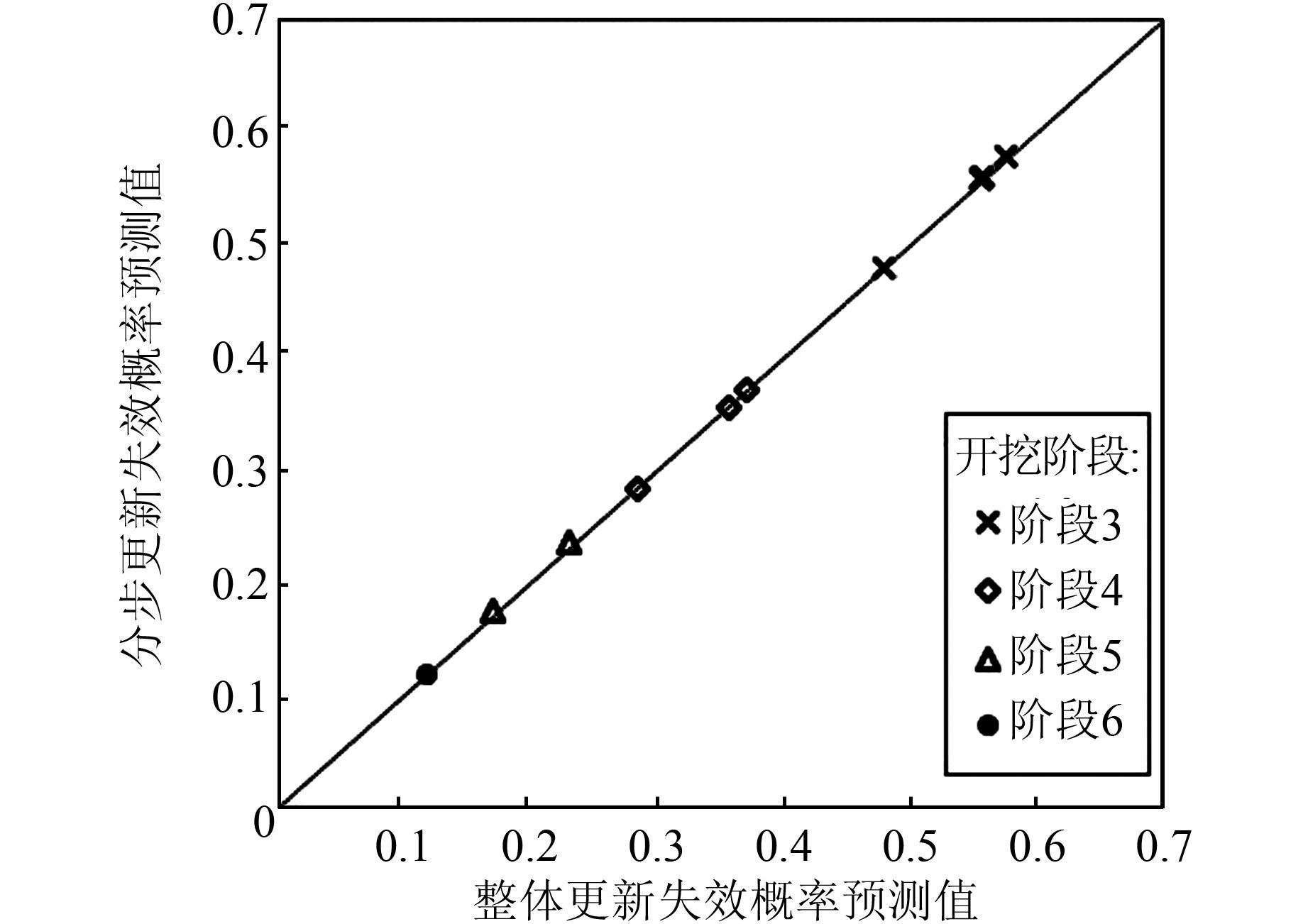
图 4和图 5所示分别为当先验分布为正态分布时分步更新与整体更新得到的最大地表沉降和失效概率预测值.由于整体更新过程中没有假设后验分布类型，因此可以以整体更新的结果为标准，衡量分步更新方法计算结果的准确性.由于在第2阶段的预测中只利用了先验信息，没有进行土体参数的贝叶斯更新，因此应从第3个阶段的预测值进行比较分析.由图 4和图 5可以看出，当先验分布为正态分布时，分步更新的最大地表沉降和失效概率预测值均比较准确.本文采用土体参数的均值计算最大地表沉降，反映了土体参数后验分布的平均水平，而失效概率反映了后验分布的尾部情况.当先验分布为正态分布时，假设正态后验分布的分步更新方法计算结果比较准确.

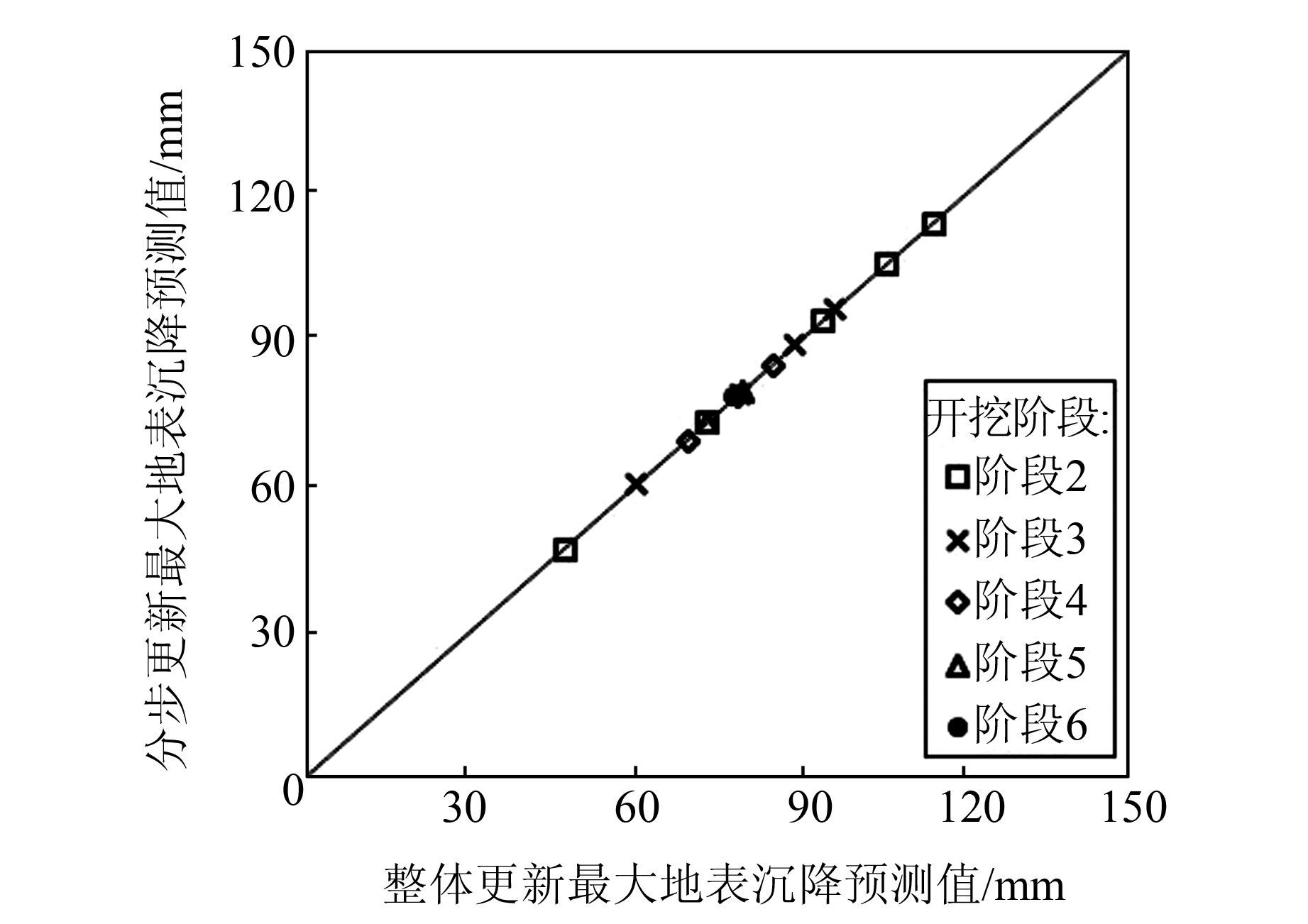
图 4 正态分布下最大地表沉降预测值比较 Figure 4 Comparison of predicted maximum ground settlements under normal distribution
图选项
图 5 正态分布下失效概率预测值比较 Figure 5 Comparison of predicted failure probabilities under normal distribution
图选项

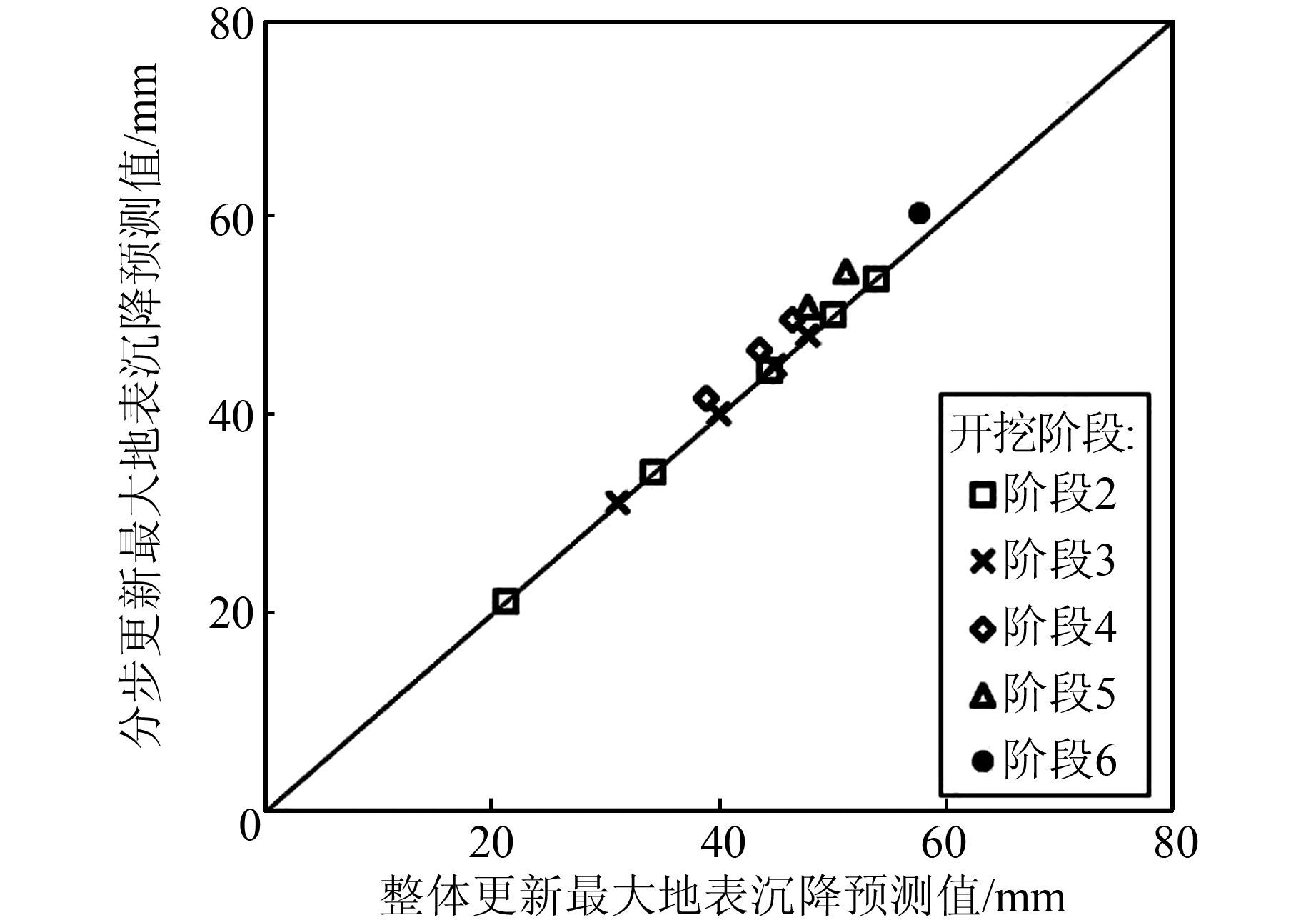
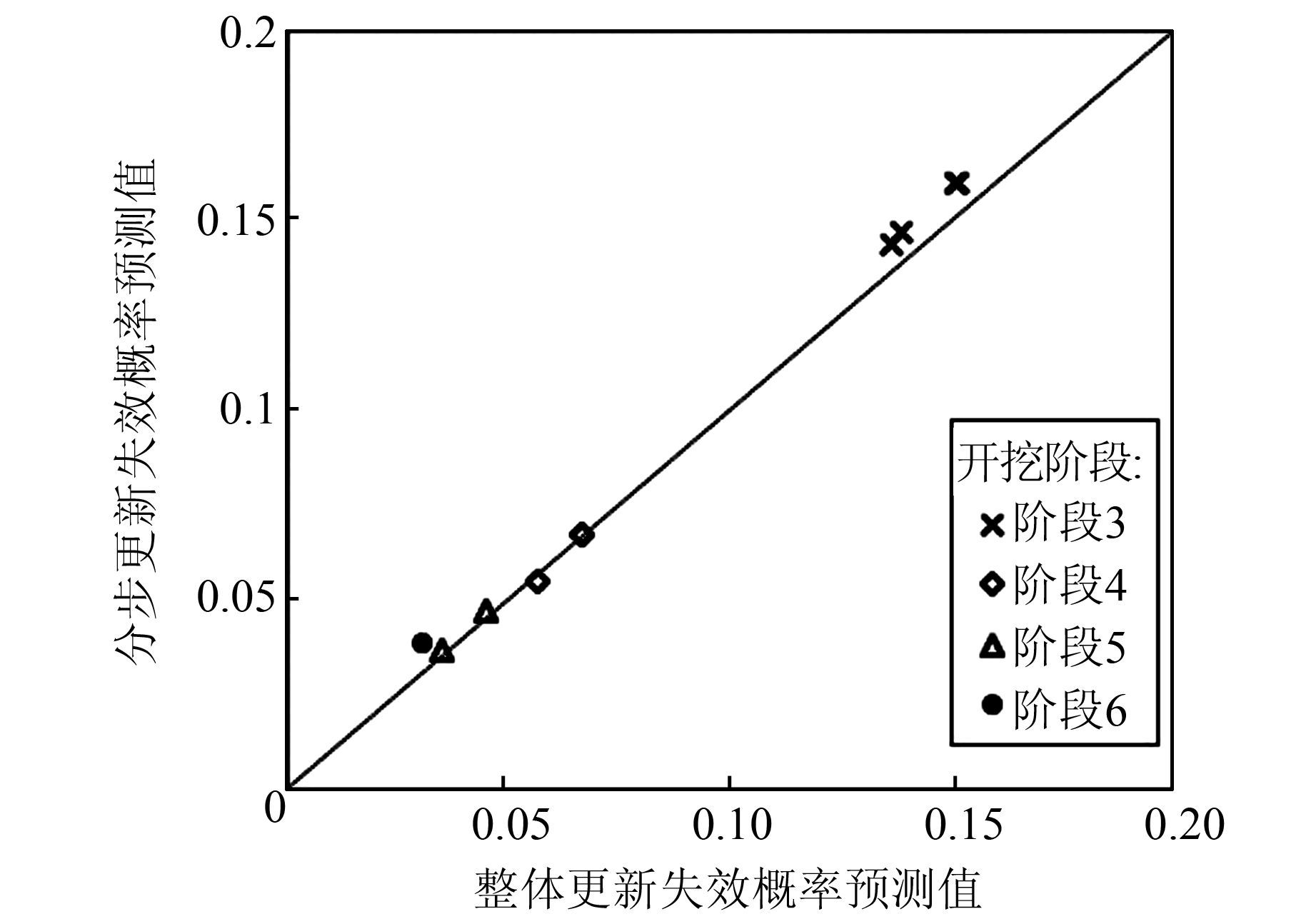
图 6和图 7所示分别为当先验分布为均匀分布时分步更新与整体更新得到的最大地表沉降和失效概率预测值.由图 6和图 7可以看出，当先验分布为均匀分布时，分步更新的计算结果和整体更新的计算结果存在显著差异，采用假设正态后验分布的分步更新方法无法准确估计最大地表沉降和失效概率.此时，整体更新方法的计算结果更加准确.

图 6 均匀分布下最大地表沉降预测值比较 Figure 6 Comparison of predicted maximum ground settlements under uniform distribution
图选项
图 7 均匀分布下失效概率预测值比较 Figure 7 Comparison of predicted failure probabilities under uniform distribution
图选项
4 结论

本文系统地比较了贝叶斯分步更新和整体更新方法，探讨了分步更新方法中假设土体参数后验分布的影响.在先验分布为正态分布和均匀分布条件下，分别采用分步更新和整体更新方法对TNEC基坑开挖过程中的土体参数进行了贝叶斯更新，并利用土体参数的更新结果预测最大地表沉降和失效概率，通过对预测值的比较研究发现:

1) 先验分布对基坑开挖过程中参数反分析的结果、最大地表沉降和失效概率预测值有显著影响；

2) 当先验分布为正态分布时，假设正态后验分布的分步更新方法能够提供合理的计算结果；

3) 当先验分布为均匀分布时，假设正态后验分布的分步更新方法的计算结果不准确，此时应采用整体更新方法.

参考文献
[1] Hsiao E C L, Schuster M, Juang C H, et al. Reliability analysis and updating of excavation-induced ground settlement for building service ability assessment[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134: 1448–1458. DOI:10.1061/(ASCE)1090-0241(2008)134:10(1448)
[2] Juang C H, Luo Z, Atamturktur S, et al. Bayesian updating of soil parameters for braced excavations using field observations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139: 395–406. DOI:10.1061/(ASCE)GT.1943-5606.0000782
[3] 徐军, 郑颖人. 基于响应面方法的围岩参数随机反分析[J]. 岩土力学, 2001, 22(2): 167–170.
Xu Jun, Zheng Yingren. Random back analysis of field geotechnical parameter by response surface method[J]. Rock Soil Mechanics, 2001, 22(2): 167–170.
[4] 张俊峰, 王建华, 陈锦剑, 等. 跨越运营地铁隧道超大基坑开挖的土体参数反分析[J]. 上海交通大学学报, 2012, 46(1): 42–46.
Zhang Junfeng, Wang Jianhua, Chen Jinjian, et al. 3-D FEM back-analysis of an over size and deep excavation[J]. Journal of Shanghai Jiaotong University, 2012, 46(1): 42–46.
[5] Zhang J, Tang W H, Zhang L M, et al. Characterising geotechnical model uncertainty by hybrid Markov Chain Monte Carlo simulation[J]. Computers and Geotechnics, 2012, 43: 26–36. DOI:10.1016/j.compgeo.2012.02.002
[6] Wang Y, Au S K, Cao Z J. Bayesian approach for probabilistic characterization of sand friction angles[J]. Engineering Geology, 2010, 114(3-4): 354–363. DOI:10.1016/j.enggeo.2010.05.013
[7] Li X Y, Zhang L M, Jiang S H. Updating performance of high rock slopes by combining incremental time-series monitoring data and three-dimensional numerical analysis[J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 83: 252–261.
[8] 赵腾远. 基于马尔科夫链蒙特卡洛的坪子山滑坡的稳定性分析[D]. 成都: 西南交通大学, 2014: 31-32.
Zhao Tengyuan. Markov Chain Monte Carlo-based stability analysis for Pingzishan landslide [D]. Chengdu: Southwest Jiaotong University, 2014: 31-32.
[9] Wang L, Ravichandran N, Juang C H. Bayesian updating of KJHH model for prediction of maximum ground settlement in braced excavations using centrifuge data[J]. Computers and Geotechnics, 2012, 44: 1–8. DOI:10.1016/j.compgeo.2012.03.003
[10] Kung G T C, Juang C H, Hsiao E C L, et al. Simplified model for wall deflection and ground-surface settlement caused by braced excavation in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133: 731–747. DOI:10.1061/(ASCE)1090-0241(2007)133:6(731)
[11] 胡文杰, 徐洪钟. 城市隧道基坑地下连续墙变形特性研究[J]. 南京工业大学学报: 自然科学版, 2015, 37(4): 97–103.
Hu Wenjie, Xu Hongzhong. Characteristic of diaphragm wall deflection due to deep excavation of municipal tunnel[J]. Journal of Nanjing University of Technology (Natural Science Edition), 2015, 37(4): 97–103.
[12] Ou C Y, Liao J T, Lin H D. Performance of diaphragm wall constructed using top-down method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 798–808. DOI:10.1061/(ASCE)1090-0241(1998)124:9(798)