文章信息
- 周海娟, 周伟, 常晓林, 马刚, 胡超
- ZHOU Haijuan, ZHOU Wei, CHANG Xiaolin, MA Gang, HU Chao
- 动力荷载下散粒体的锚杆加固效应
- Anchoring effect of granular mixture under dynamic loads
- 武汉大学学报(工学版), 2016, 49(6): 818-823
- Engineering Journal of Wuhan University, 2016, 49(6): 818-823
- http://dx.doi.org/10.14188/j.1671-8844.2016-06-004
-
文章历史
- 收稿日期: 2015-10-19
2. 武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072
2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University, Wuhan 430072, China
散粒体材料广泛存在于岩土工程中,如人工堆石料、破碎岩体、煤矿巷道等,是由大小不等、形状各异的块石组成的松散集合体.在岩土工程中通常采用锚固技术来控制岩土工程的变形,提高其稳定性.锚固技术作为一种经济、有效、主动的岩体加固方法,对散粒体结构的稳定性发挥着重要作用,如为了防止在地震中坝顶堆石体的松动、滑落,青峰岭水库、冶勒、长河和糯扎渡等均采用土工格栅或锚杆对坝顶堆石区进行加固.近几年来,我国西南地区地震频发,在高地震烈度区的堆石坝以及边坡破碎岩体等的稳定问题受到严峻的考验,例如紫平铺面板堆石坝经受汶川地震后,下游坝坡靠近坝顶附近的干砌石松动、翻起,并向下滑移,如图 1所示.但是动力荷载下散粒体锚固的设计理念和计算方法尚不够完善,不能在设计阶段提出科学、合理的锚固方案和锚固效果的评价方法.因此研究动力荷载作用下散粒体的锚杆加固效应具有重要的意义.

|
| 图 1 紫平铺大坝震后破坏图 Figure 1 Earthquake damage of Zipingpu dam |
目前散粒体锚固效应研究主要集中在静力荷载、长期荷载方面.李术才[1]等采用加锚断续节理岩体的断裂损伤模型来模拟锚杆的支护作用.吕庆[2]等结合现场检测和室内试验资料,对破碎岩质高边坡的预应力锚杆技术进行系统的数值模拟分析.姜清辉[3]、张秀丽[4]等人采用非连续变形分析方法模拟了锚杆在节理岩体中的加固作用.美国陆军工程师团水道试验站曾对砾石加锚进行试验来研究散粒体的锚杆加固机制[5].马刚[6]等人通过细观数值试验研究了锚杆加固在散粒体中的作用机制,指出锚杆加固能显著提高散粒体的抗剪强度和整体性.胡超[7]等对砾石锚固试验进行了数值模拟,分析了加锚密度与其颗粒粒径的关系对散粒体力学性质的影响.
在动力方面,Tannant[8]等通过现场试验,研究了端部固定锚杆在爆炸荷载作用下的动力响应.Ortlepp[9]等人通过试验研究了静力和动力荷载作用下高应力隧道的加固形式及锚杆的冲击荷载测试,指出屈服锚杆可以吸收大量能量而不使隧道发生破坏.徐景茂[10]等通过模型试验和数值模拟计算,对全长粘结式锚杆加固的洞室进行抗爆性能研究.叶海林[11]等对锚杆支护岩质边坡在地震作用下的动力特性进行了数值分析,研究了锚固边坡在不同地震波作用下的抗震效果及动力稳定性,并分析其破坏机理.王建[12]等通过数值计算研究了边坡岩石块体的地震动反应特性及块体锚固效应.薛道成[13]等建立了锚杆横向振动时的动力学模型,研究了锚杆托盘与围岩之间的接触特性.言志信[14]等研究了地震作用下锚固上覆红黏土岩体边坡及锚杆的动力响应规律,指出地震作用下锚杆的支护加大了边坡的延性,限制了边坡的变形,具有很好的抗震性能.
上述研究表明锚杆在边坡支护等作用中使结构具有很好的抗震性能,本文在锚杆加固散粒体静力加载试验的基础上,对动力荷载条件下的散粒体锚杆加固效应进行研究.采用随机散粒体不连续变形方法(SGDD),建立不同锚杆间距和不同颗粒粒径以及无锚杆的数值试样,对锚杆施加一定的锚固预应力,分析散粒体材料在水平方向动力荷载下的宏观和细观力学特性,探讨加锚密度与颗粒粒径的关系对散粒体材料动力荷载条件下力学性质的影响.
1 数值试样与细观参数 1.1 数值试样的制备散粒体材料的颗粒形状和空间分布具有显著的随机性,根据颗粒级配、粒径、形状、孔隙率等生成三维多面体颗粒及其在空间中的分布[15].采用二阶四面体单元对生成的多面体颗粒进行离散,同时采用弹脆性损伤模型描述细观单元的力学行为[16].
数值试样以文献[5]中模型为参考,数值试样的外框架尺寸为0.6 m×0.6 m×0.15 m,锚杆直径为4 mm,长为150 mm,上下承托结构为直径20 mm的圆盘,锚杆示意图见图 2.锚杆为摩擦型锚杆,通过杆体与散粒体相互接触、挤压产生摩擦阻力,同时上下承托板对散粒体形成径向阻力.由于杆体与承托板在起锚固作用时可以发生变形和屈服,故采用可变形实体单元进行模拟.本文只研究水平方向的动力荷载作用,不考虑铅直方向动荷载,故采用随机模拟技术生成多面体颗粒,在框架内振捣压实后形成数值试样,如图 3所示.

|
| 图 2 锚杆示意图 Figure 2 Sketch of anchor |

|
| 图 3 数值试样 Figure 3 Numerical model |
在本文的细观数值模拟中,研究了加锚密度与颗粒粒径的关系对动力荷载条件下散粒体力学性质的影响,共生成6个数值试样,其中包括无锚杆的数值试样,如表 1所示.试样的锚杆间距分别为0.075、0.10、0.12、0.13、0.14 m,数值试样的颗粒粒径在50~52 mm之间均匀分布,生成的颗粒数为1 477,网格离散后的实体单元数为90 175,节点数为200 443.
| 试样编号 | 锚杆间距/m | 孔隙率/% | 锚杆间距与颗粒平均粒径之比 |
| 试样1 | 0.075 | 39.86 | 1.47 |
| 试样2 | 0.10 | 39.92 | 1.96 |
| 试样3 | 0.12 | 39.95 | 2.35 |
| 试样4 | 0.13 | 39.96 | 2.55 |
| 试样5 | 0.14 | 39.97 | 2.94 |
| 试样6 | 无 | 40.00 | - |
细观力学参数的取值是进行数值试验的关键.本文的散粒体材料不针对具体工程,通过类比散粒体三轴数值试验,在一般的参数取值范围内选取一组细观参数进行数值模拟,见表 2.颗粒之间的接触模型采用线性接触刚度模型,所需的细观参数包括:颗粒之间的法向和切向接触刚度kn、ks,颗粒间的内摩擦角φu,颗粒的单轴抗压强度fc,散粒体和锚杆的弹性模量E、泊松比ν、密度ρ,锚杆的线膨胀系数α,锚杆的抗拉强度ft.
| 散粒体 | E/ GPa | ν | ρ/ (g·cm-3) | fc/MPa | φu/ (°) | kn/ (N·m-1) | ks/(N·m-1) |
| 40 | 0.2 | 2.18 | 120 | 45 | 11×109 | 7.5×109 | |
| 锚杆 | E/GPa | ν | ρ/(g·cm-3) | α | ft/MPa | ||
| 207.8 | 0.3 | 7.80 | 1.2×10-5 | 235 |
研究加锚密度与颗粒粒径的关系对动力荷载条件下散粒体锚固效应的影响,此时对6个数值试样施加相同的预应力.首先固定外框架,通过降温法对锚杆施加预应力,锚杆受到温降荷载发生收缩,通过锚杆与散粒体的接触、连接将锚杆的收缩应变传递到散粒体中,达到施加预应力的效应.同时,对整个结构系统施加重力作用.
降温法模拟预应力的预应力值与温降的关系为
σ=E·α·ΔT
式中:E和α分别为锚杆的弹性模量和线膨胀系数.此处预应力值取锚杆抗拉强度的50 %,对应的温降为47 ℃.
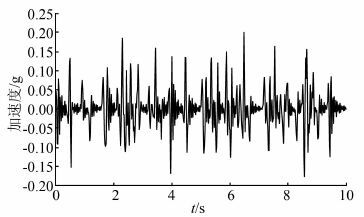
然后,释放外框架在水平方向的位移约束,并在水平方向输入峰值加速度为0.2g的水平地震波(相当于Ⅷ度基本烈度),地震波持续时间为10 s,截取自汶川实测地震波,地震波加速度时程曲线如图 4所示.计算输入的地震波进行了过滤和基线校正.
|
| 图 4 计算时输入的地震波加速度时程曲线 Figure 4 Time-history curve of horizontal seismic acceleration |
试样1在动力荷载作用后的稳定状态如图 5所示,整个结构在重力及水平方向的地震波作用下,少量颗粒散落,整个结构处于稳定状态,体现了加锚在动力荷载作用下可以限制散粒体变形、提高散粒体整体性.从试样沿锚杆布置方向的剖面图可以看出,散落的颗粒大多位于锚杆之间未受到锚固力作用的区域,也有少部分锚杆附近的颗粒由于初始制样时未被压实、处于锚杆锚固作用区域外而散落.

|
| 图 5 试样1的稳定状态 Figure 5 Steady state of model 1 |
图 6给出了试样2和试样3的最终稳定状态.从表 1可以看出,试样1、2、3的锚杆间距与颗粒粒径之比分别为1.47、1.96、2.35,结合图 5、图 6可知,锚杆间距与颗粒粒径之比越小,即锚杆布置越密时,散落的颗粒数越少,锚固效果越好.

|
| 图 6 稳定状态 Figure 6 Steady state |
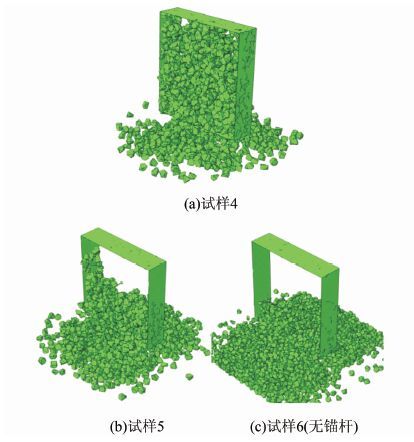
试样4、5在动力荷载作用后的变形状态如图 7(a)和图 7(b)所示,散粒体结构未受到锚固作用区域的颗粒大量掉落,剩余的散粒体不足以填充框架来保证预应力的挤压,在重力及地震波的双重作用下,留在框架内的其余颗粒也逐渐掉落,最终整个散粒体结构溃散.试样6无锚杆,在动力加载初期便全部溃散,如图 7(c)所示.
|
| 图 7 变形状态 Figure 7 Deformation of model 4, 5 and model 6 |
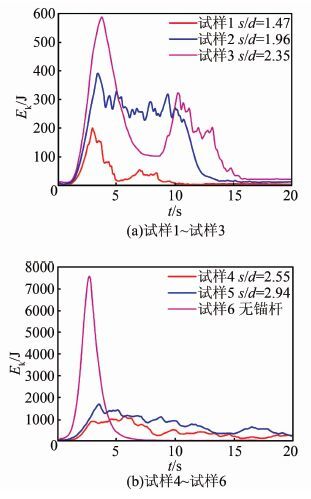
图 8为试样1~6的总动能变化曲线,横坐标为时间,s/d为锚杆间距与克里平均粒径之比.t=0~0.3 s时对锚杆施加预应力,颗粒之间发生挤压、相互转动、滑移,产生微小动能,随后动能又迅速减小.t=0.3~2 s,表面松散的颗粒开始掉落,动能开始增加.t=2 s时,在水平方向输入地震波,结构开始晃动,在锚杆锚固区域之外的颗粒开始大量掉落,试样的动能急剧增大.数值计算时,试样下方1 m处布置一承接板,当大量掉落的颗粒在承接板上静止时,动能达到最大值.随着时间的推移,在地震波的作用下,框架内的颗粒重新排列,局部孔隙率变大,少量颗粒继续掉落,动能重新增大,但幅度较小,如试样1和试样3;试样2的颗粒在动力加载初期相继掉落,间隔时间较短.最后,试样1、2、3中的加锚散粒体动能逐渐趋于稳定,散粒体形成了新的稳定结构.但是,试样4在动力加载初期,颗粒大量散落,动能急剧增大,试样顶端散粒体被掏空,中间散粒体局部溃散;试样5在动力加载初期,锚杆不足以加固散粒体结构,大量颗粒散落,顶端开始溃散,随着时间的推移,更多颗粒脱落,结构迅速溃散,锚固作用均失效,整体性被破坏.试样6无锚杆加固,在加载初期,结构整体溃散.
|
| 图 8 动能变化曲线 Figure 8 Curves of kinetic energy |
6个数值试样在动力荷载下的动能峰值及稳定时间或失稳时间统计见表 3.
| 试样编号 | s/d | 动能峰值/J | 稳定时间/s | 失稳时间/s |
| 试样1 | 1.47 | 204.2 | 10.5 | - |
| 试样2 | 1.96 | 400.1 | 13.6 | - |
| 试样3 | 2.35 | 590.9 | 16.2 | - |
| 试样4 | 2.55 | 1180.8 | - | 6.4 |
| 试样5 | 2.94 | 1705.1 | - | 4.2 |
| 试样6 | 无锚杆 | 7575.7 | - | 2.7 |
从表 3可知,随着锚杆间距与颗粒粒径比值的增大,散粒体试样的动能峰值增大.原因是处于锚固作用区外的颗粒增多,在后续的动力荷载作用下,局部孔隙率增大,结构松散,初期和后期掉落的颗粒都增多,动能增大.另外,对于稳定的试样,锚杆间距与颗粒粒径比值越大,结构达到稳定需要的时间越长;相反,对于失稳的试样,锚杆间距与颗粒粒径比值越大,结构整体溃散的时间越短.可见,锚杆可以显著限制散粒体结构的变形,缩短散粒体结构在动力荷载下的稳定时间或减缓失稳,提高其整体稳定性.
根据试样3最终的变形,加载结束后,虽然大部分颗粒仍停留在框架内,整个结构稳定,但是局部区域掉落的颗粒较多,可能导致局部破坏.
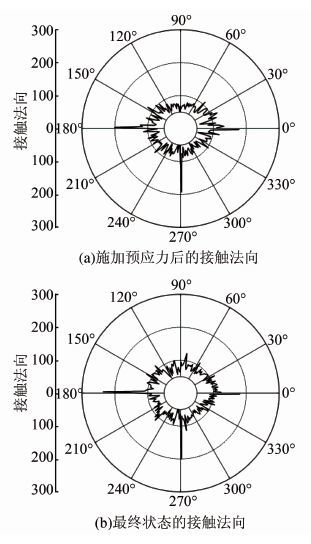
3.3 各向异性演化规律散粒体材料的宏观力学特性与其细观组构在加载过程中的演化规律关系密切.对于散粒体材料,颗粒的组成、排列方式及接触力是决定其宏观力学特性的主要因素,故提取颗粒间的接触法向、法向接触力的各向异性演化,将其投影在XY平面来观察细观组构的演化规律.以试样1为例,每2°作为一个区间,分别绘制加锚散粒体施加完预应力以及动力荷载加载结束后最终稳定状态时的细观各向异性分布图,如图 9、图 10.
从图 9可以看出,施加完预应力后,水平方向的侧向接触数较多,此时接触法向大致呈椭圆状;水平方向动力作用加载完直至最终,试样在竖直方向的接触数有所增加,接触法向的各向异性减弱.
|
| 图 9 接触法向各向异性分布图 Figure 9 Diagrams of contact orientation anisotropy |
|
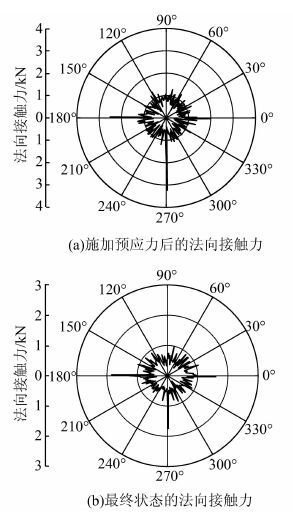
| 图 10 法向接触力各向异性分布图 Figure 10 Diagrams of contact normal force anisotropy |
从图 10可以看出,施加完预应力后,试样的法向接触力在重力方向最大,水平方向明显大于其他区域,法向接触力总体呈现圆形趋势;达到最终稳定状态时,试样总体的法向接触力相较于之前明显减小,水平方向与重力方向的接触力明显大于其他区域,说明在加载过程中,预应力产生的侧向压力增强了水平方向的法向接触力,控制了试样的变形.
4 结论1) 采用随机散粒体不连续变形方法,进行了动力荷载下加锚散粒体的数值模拟,数值模拟结果可以反映散粒体在不同加锚密度时的变形规律及加固效应.
2) 对比加锚和无锚的两种情况,锚杆加固可以有效限制散粒体在动力荷载时的变形,显著提高散粒体的整体性.
3) 散粒体材料的宏观特性与其细观组构在加载过程中的演化规律关系密切.分析试样颗粒间的接触法向、法向接触力的各向异性演化得出,由于锚杆的挤压使散粒体产生侧向压力,加强了颗粒间的侧向接触力.
4) 加锚密度对锚杆加固效果至关重要.锚杆长度相同的情况下,加锚密度越大,颗粒散落越少,结构稳定所需时间越短,锚杆效果越好,散粒体试样的抗震性能越好.当锚杆间距与散粒体平均粒径的比值小于2.35时,锚杆可以有效地限制散粒体的变形,很好地提高其自稳能力而保持整体稳定.
| [1] |
李术才, 王刚, 王书刚, 等. 加锚断续节理岩体断裂损伤模型在硐室开挖与支护中的应用[J].
岩石力学与工程学报, 2006, 25(8): 1582–1590.
Li Shucai, Wang Gang, Wang Shugang, et al. Application of fracture-damage model to anchorage of discontinuous jointed rockmass of excavation and supporting[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(8): 1582–1590. |
| [2] |
吕庆, 孙红月, 尚岳全, 等. 破碎岩质边坡预应力锚固机制数值模拟研究[J].
岩石力学与工程学报, 2006, 25(9): 1848–1856.
Lü Qing, Sun Hongyue, Shang Yuequan, et al. Numerical simulation study on prestressed anchorage mechanism in a crushed rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1848–1856. |
| [3] |
姜清辉, 丰定祥. 三维非连续变形分析方法中的锚杆模拟[J].
岩土力学, 2001, 22(2): 176–178.
Jiang Qinghui, Feng Dingxiang. Modeling of rockbolts in three-dimensional discontinuous deformation analysis[J]. Rock and Soil Mechanics, 2001, 22(2): 176–178. |
| [4] |
张秀丽, 焦玉勇, 刘泉声. 非连续变形分析方法中的预应力锚杆模拟[J].
地下空间与工程学报, 2008, 4(1): 38–41.
Zhang Xiuli, Jiao Yuyong, Liu Quansheng. On modeling of pre-tension bolt in discontinuous deformation analysis method[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(1): 38–41. |
| [5] | Evert H. Practical Rock Engineering[M]. Evert Hoek Consulting Engineer Inc., 2007. |
| [6] |
马刚, 周伟, 常晓林. 等, 锚杆加固散粒体的作用机制研究[J].
岩石力学与工程学报, 2010, 28(8): 1577–1584.
Ma Gang, Zhou Wei, Chang Xiaolin, et al. Study of anchorage mechanism of granular mixture[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 28(8): 1577–1584. |
| [7] |
[7]胡超, 周伟, 常晓林. 散粒体中锚杆间距的锚固效应研究[J].
岩土力学, 2014, 35(7): 2088–2094.
Hu Chao, Zhou Wei, Chang Xiaolin, et al. Study of anchoring effect of anchor spacing in granular mixture[J]. Rock and Soil Mechanics, 2014, 35(7): 2088–2094. |
| [8] | Tannantf D D, Brummerf R K, Y I X. Rock bolt behavior under dynamic loading: Field tests and modeling[J]. International Journal of Rock Mechanics and Mining Sciences, 1995, 32(6): 537–550. DOI:10.1016/0148-9062(95)00024-B |
| [9] | Ortlepp W D, Stacey T R. Performance of tunnel support under large deformation, static and dynamic loading[J]. Tunnelling and Underground Space Technology, 1998, 13(1): 15–21. DOI:10.1016/S0886-7798(98)00022-4 |
| [10] |
徐景茂, 顾金才, 陈安敏, 等. 锚杆长度和间距对洞室抗爆性能影响研究[J].
岩土力学, 2012, 33(11): 3489–3496.
Xu Jingmao, Gu Jincai, Chen Anmin, et al. Study of anti-explosion ability of reinforced tunnels with different anchor lengths and spacings[J]. Rock and Soil Mechanics, 2012, 33(11): 3489–3496. |
| [11] |
叶海林, 黄润秋, 郑颖人, 等. 岩质边坡锚杆支护参数地震敏感性分析[J].
岩土工程学报, 2010, 32(9): 1374–1379.
Ye Hailin, Huang Runqiu, Zheng Yingren, et al. Sensitivity analysis of parameter for bolts in rock slopes under earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1374–1379. |
| [12] |
王建, 姚令侃, 蒋良潍. 边坡岩石块体动力响应及锚固抗震效应研究[J].
公路交通科技, 2010, 27(3): 6–11.
Wang Jian, Yao Lingkan, Jiang Liangwei. Research on dynamic response of rock blocks in slope and anti-seismic effect of anchor reinforcement to rock mass[J]. Journal of Highway and Transportation Research and Development, 2010, 27(3): 6–11. |
| [13] |
薛道成, 张凯. 煤矿锚杆锚固结构系统横向振动特性研究[J].
中国矿业大学学报, 2013, 42(4): 695–700.
Xue Daocheng, Zhang Kai. Theoretical research on transverse vibrations of the bolt anchorage structure in coal mine[J]. Journal of China University of Mining & Technology, 2013, 42(4): 695–700. |
| [14] |
言志信, 张刘平, 江平, 等. 锚固上覆红黏土岩体边坡的地震动力响应[J].
岩土力学, 2014, 35(3): 753–758.
Yan Zhixin, Zhang Liuping, Jiang Ping, et al. Dynamic response of anchoring overlying red clay rock slope under earthquake action[J]. Rock and Soil Mechanics, 2014, 35(3): 753–758. |
| [15] |
周伟, 常晓林, 周创兵, 等. 堆石体应力变形细观模拟的随机散粒体不连续变形模型及其应用[J].
岩石力学与工程学报, 2009, 28(3): 491–499.
Zhou Wei, Chang Xiaolin, Zhou Chuangbing, et al. Stochastic granule discontinuous deformation model of rockfill and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 491–499. |
| [16] |
马刚, 周伟, 常晓林, 等. 堆石体三轴剪切试验的三维细观数值模拟[J].
岩土工程学报, 2011, 33(5): 746–753.
Ma Gang, Zhou Wei, Chang Xiaolin, et al. 3D mesoscopic numerical simulation of triaxial shear tests for rockfill[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 746–753. |
 2016, Vol. 49
2016, Vol. 49




