文章信息
- 何珊, 梁红梅, 蒋劲, 肖志怀
- HE Shan, LIANG Hongmei, JIANG Jin, XIAO Zhihuai
- 小波分形算法在旋转机械振动信号特征提取中的应用
- Application of wavelet fractal algorithm to feature extraction of rotating machinery vibration signals
- 武汉大学学报 (工学版), 2017, 50(1): 129-136
- Engineering Journal of Wuhan University, 2017, 50(1): 129-136
- http://dx.doi.org/10.14188/j.1671-8844.2017-01-020
-
文章历史
- 收稿日期: 2016-08-12
2. 新疆昌吉职业技术学院, 新疆 昌吉 831100
2. Changji Vocational and Technical College, Changji 831100, China
旋转机械正在向大型化、复杂化、大功率方向发展,机组结构日趋复杂,集成化程度越来越高, 其安全性和稳定性已成为电力行业关注的焦点.由于旋转机械的特殊性,引起机组故障的原因错综复杂,故障征兆和故障原因之间表现为很强的随机性和不确定性,如何从大量实时状态信息中提取有用的机组故障特征是旋转机械故障诊断的难点之一.实际证明:振动信号携带丰富的机械设备运行状态信息,80%的机组故障在振动信号中更有反映[1].因此,从振动信号中提取出有效的旋转机械故障特征是故障诊断过程中至关重要的一步.目前,振动信号主要分析方法是对其频率结构的分析,如快速傅里叶 (FFT) 分析、短时傅里叶 (STFT) 分析以及高阶累积量谱分析等等,这些方法着重于从振动信号中提取一些有效的故障特征,并已经取得了良好的效果.将这些特征提取方法与模式识别理论如神经网络、RBF网络、贝叶斯网络等[2-6]相结合,可实现对机械振动状态的在线监测及其故障的智能在线识别.
随着非线性动力学研究的不断进步,特别是混沌时间序列信号的相空间重构理论的发展,在设备故障诊断领域出现了基于相空间重构的分形故障特征提取方法.包括分形理论在内的非线性动力学研究方法从全新的角度更深刻地解析了复杂非线性动力系统的故障行为,同时也为从混沌现象中解释故障的本质提供了理论基础.而旋转机械作为一个非线性复杂系统,其振动信号通常显现出非平稳和暂态特性,甚至是随机振动信号,这些信号在某种程度上展现出分形特性[7].分形理论为复杂信号提供了一种几何结构分析方法,近年来已在旋转机械以及其他领域的故障诊断中有了有效的应用:马晋、江志农等将混沌分形理论的特征提取技术应用于气阀故障诊断中[8]; Y. J. Jiang、Y. Tanabashi等将一个三维分形估计法用于岩石节理面,并研究了表面分形特性与液压机械特性之间的关系[9];在机械设备故障诊断中,将分形几何算法引入机械信号分析,得到了良好的效果[10].
近年来,小波分形理论在振动信号特征提取中已有较为显著的应用效果.然而,由于该方法较为新颖,目前只在滚动轴承领域中得到了应用[11].考虑到旋转机械振动信号和滚动轴承振动信号之间的相似性,本文将小波分形理论引入到旋转机械领域.通过小波函数分解已降噪的振动信号,利用各层细节成分的方差表征振动信号在各层的能量分配,以层数为横坐标,方差对数为纵坐标拟合出一条直线,对该直线的斜率进行一定的数学运算得到振动信号的分形维数.利用转子机械试验台系统仿真旋转机械故障,采集相应的故障振动信号,并分别用小波分形算法和传统分形算法进行分析比较,实验分析结果表明这两种方法均在特征提取方面有较好效果,但小波分形算法有更高的准确性.
1 分形维数及GP算法 1.1 分形维数非线性动态混沌理论常用于描述非周期性的宽频信号,在机械设备故障诊断领域中,最常用的混沌理论是分形几何原理.分形维数是度量分形的重要指标,有许多种分形维数可被用来刻画信号的复杂度,不同的分形维数定义方式也不同,但其本质是大致相同的:在某种尺度下度量分形图形或者分形信号,然后将分形维数表达为测量结果与测量尺度之比.常见的分形维数有Haus-dorff维数、自相似维数、盒维数、容量维、关联维数、信息维等[12].例如,严格自相似的自相似维数D定义如下[13]:
假设分形整体集S由N个非重叠的部分s1, s2, s3, …, sN组成,并且每一部分si经过放大1/ri倍后可与S全等 (0 < ri < 1, i=1, 2, …,N),并且ri=r,则相似维数定义为
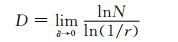 (1)
(1)
相似维数的使用范围是有限的,只有严格相似的分形图形才能用该维数进行描述.而实际上,大多数分形图形都不是严格相似的,如某些随机图形或随机信号.因此,其应用范围也受到了限制.
1.2 关联维数和GP算法分形维数可以定量地刻画混沌吸引子的特征,在众多分形维数中,关联维数对吸引子的不均匀性反应敏感,更能反映吸引子的动态结构,能较好地反映颗粒的分形性质.Grassberger和Procaccia根据嵌入理论和相空间重构思想,提出了从时间序列直接计算关联维数的GP算法[14],因该算法计算简单可靠,在故障诊断领域常用于处理时域序列的信号并计算其关联维数.
已知给定的时间序列{χ1, χ2, …, χn},采用时间延迟法将其扩充到m维欧氏空间Rm中,得到观测序列的新集合,其中元素记为[14]
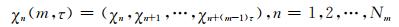 (2)
(2)
式中:τ=kΔt,为延迟时间,k为整数;Nm=N-(m-1)τ, N为信号序列点数.
以矩阵X Nm×m的行向量X i(i=1, 2, …,Nm) 为重构空间中的点,取正数r, 检查在时间序列中有多少“点对”(X i, X j)|i≠j之间的距离‖ X i-X j‖比正数r小,把小于该距离的“点对”数占总数的比例记为c(r):
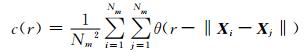 (3)
(3)
其中,θ(x) 为Heaviside函数:
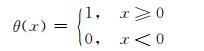 (4)
(4)
正数r的取值并非随意选取,若过大,则几乎所有“点对”的距离都将小于r,此时的c(r) 也将无法描述出系统特性.将r适当缩小可得到在某段区间内c(r) 随r的变化:
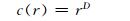 (5)
(5)
其中,D即为所需的关联维数.该区间称为无标度区间,则关联维数具体的求解公式为
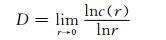 (6)
(6)
因此,以lnr为横坐标,lnc(r) 为纵坐标,则在无标度区间内 (lnc(r)-lnr) 变化曲线的斜率即为D.同时,嵌入维数m的选取也对D的大小有影响,由文献[15]可知,当m≥2k+1时 (k为吸引子的维数),D的大小将与m无关而稳定在一个值.对于G-P算法,已有文献对其进行了参数优化和改进,例如嵌入维数的选取原则、r的取值范围等,在实际计算时,应遵循这些原则[15].
2 小波分形算法 2.1 小波分形组合可行性小波分析是一种系统论方法,其分析过程主要利用了局部对整体的依赖性;而分形理论则通过研究局部信号来确定信号的整体特性.越来越多的研究成果使得人们意识到,小波变化和分形理论之间有着十分密切的联系[16].
分形理论认为,事物整体与其组成部分具有自相似性,这包括严格自相似性、统计自相似性.根据分形理论,集合F可以由紧支撑集的函数β(t) 生成,即:
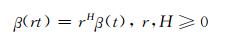 (7)
(7)
式中:r是自相似仿射算子; H是与维数有关的参数.
由小波理论可知,母小波 (mother wavelet)ψ(t) 经过平移和收缩可得到函数族|ψa, b(t)|:
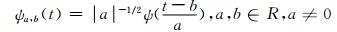 (8)
(8)
式中:a为伸缩因子; b为平移因子.
对比上述两式可得出,分形的自相似仿射算子r与小波变换的伸缩因子a是一致的,因而可以说小波变换和分形理论具有相似性.上述小波变换与分形理论从认识事物的过程和本质上的一致性,确保了小波分形组合算法的可行性.
2.2 小波分形算法分形理论在描述具有非线性、随机对象以及空间物体方面有着广泛应用,例如,在描述具有白噪声和布朗运动属性的时间序列信号中,分形理论就呈现出了非常良好的效果[17-19].这些具有白噪声和布朗运动属性的信号都是典型的1/f过程模型,该模型已经成功应用于物理和生物研究中.1/f过程模型的功率谱密度函数有如下关系[17-19]:
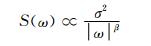 (9)
(9)
其中:ω为角频率; σ2代表的是原始信号的方差; β则是频谱的细节参数,表征不同频带间的功率谱密度的拟合直线的斜率.特别地,对于白噪声信号,β=1;对于布朗运动信号,β=2.在表征信号自相似特性的参数H和β之间有如下函数关系:
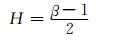 (10)
(10)
对于一维信号:
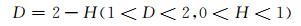 (11)
(11)
于是可推得:
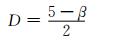 (12)
(12)
尽管并不是严格的1/f过程,机械振动的非线性特征和分形特性也与1/f过程较为相似.1/f过程的功率谱集中于低频段,而旋转机械故障振动信号的频谱则分布于低频及中高频带,其功率谱如下:
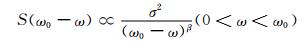 (13)
(13)
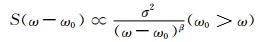 (14)
(14)
其中, ω0为功率谱峰值中心的频率.将故障诊断信号的功率谱和严格1/f过程的功率谱进行比较,发现两者仅存在一个频移,因此它们之间存在相似性.
在小波分形算法中,每一个频段的范围是由小波分解所决定的.采用正交小波进行小波分解,得到各层细节分量d2j的频率范围如下:
 (15)
(15)
其中, fs是采样频率.
分解后的功率谱则变为
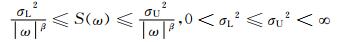 (16)
(16)
零均值信号的功率谱S(ω) 可由其第j层细节成分分量的方差Var (d2j) 所表示.对连续时间信号x(t),构造零均值信号只需对原始信号进行处理时将信号减去其均值ms即可.
设自相关函数R(τ),其与信号功率谱S(ω) 之间的关系可由下式给出:
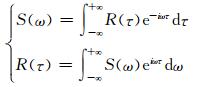 (17)
(17)
因此,信号的方差可表示为
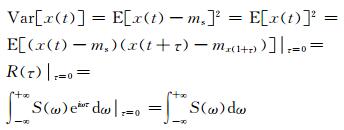 (18)
(18)
连续信号x(t) 的积分运算∫和期望运算E分别对应着离散信号x(n) 的求和运算和均值运算.因此,对于零均值的离散信号x(n),其方差与功率谱是等价的:
 (19)
(19)
可得:
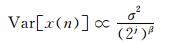 (20)
(20)
其中, β是在各尺度j下,其方差对数所拟合直线的斜率.
细节成分d2j的方差定义为
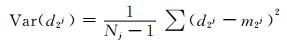 (21)
(21)
其中:md2j是尺度j下的细节成分d2j的均值; Nj表征了尺度j下细节成分d2j的采样数,即待分析信号的采样数.
小波分形算法的信号处理过程如图 1.
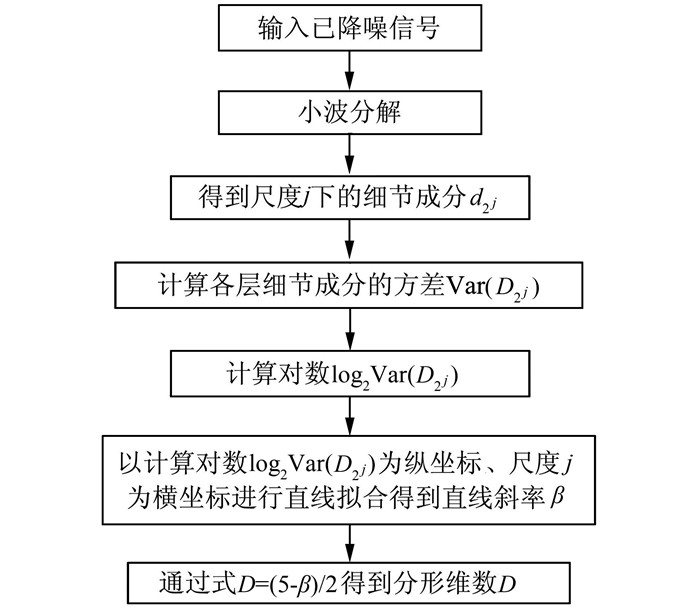
|
| 图 1 小波分形算法过程示意图 Figure 1 Signal processing progress of wavelet fractal algorithm |
为验证小波分形算法的有效性,本节应用转子试验台得到了多组实验数据并进行了验证试验.
3.1 数据获取本文利用如图 2所示的转子机械试验台系统.该系统可以仿真出机组的不平衡、不对中、碰磨等多种故障,主要由一台直流电机驱动,并利用DH5600转速控制器控制转速.转子直径为10 mm,长850 mm,由两段转轴经过法兰连接而成,并由4个轴承支承.转子上安装2个直径为75 mm的转盘.另外,有2个碰磨螺纹箱安装在系统支架上.该系统的传感器主要包括:用于测量摆度的2个电涡流传感器,用于测量转速的光电传感器,用于测量振动的压电加速度传感器.由传感器采集的摆度信号和振动信号被传输给前置器,进行放大、滤波,并最终传输给计算机进行存储、显示和分析.

|
| 图 2 转子试验台 Figure 2 Experimental machinery system |
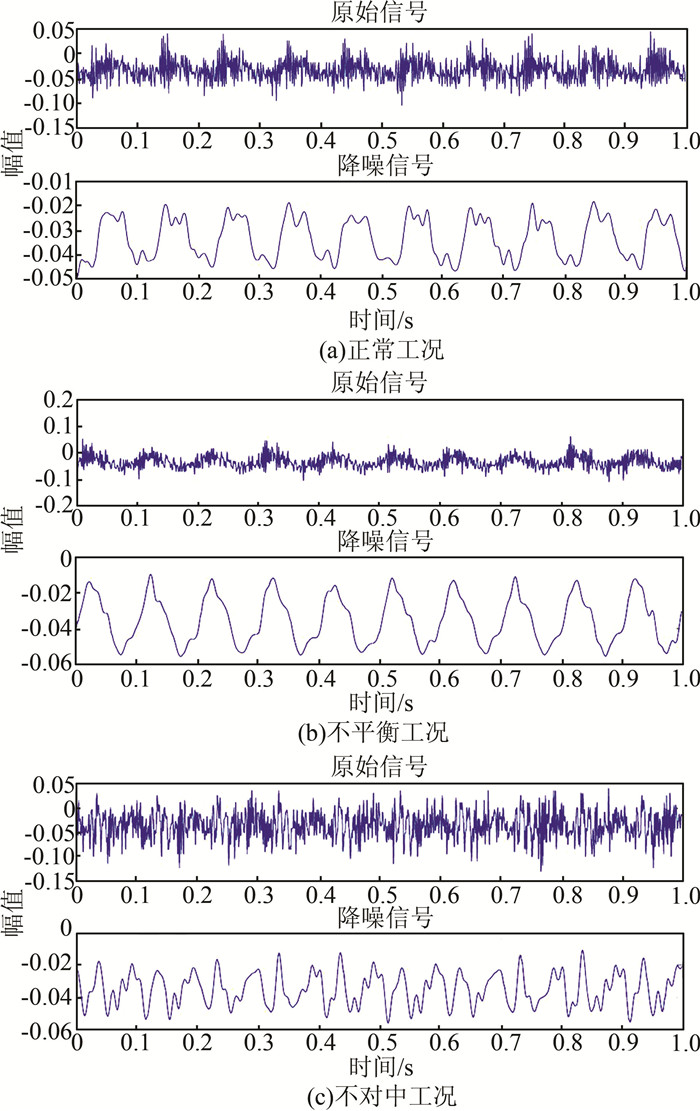
分别采集正常工作状态、不平衡故障工况和不对中振动故障信号,用于进行信号特征提取方法的研究.其中,不平衡故障工况由在转盘接近边缘处的螺纹孔内旋入2 g的质量块进行模拟;不对中故障工况则通过措置法兰处两轴位置实现.在信号采集过程中,机组转速设为1 200 r/min,采样频率设为2 048 Hz,对每种机组状态分别采集30组数据,每组数据包括2 048个点.图 3所示为一组原始采集信号及相应降噪后的信号.
|
| 图 3 不同工况下的原始信号和降噪信号 Figure 3 The original and denoised signals under different conditions |
从图 3可以看出,原始信号中混杂着大量的噪音,各种状态信号特征也变得模糊,很难从原始信号中看出不平衡工况和正常状态信号之间的区别,本文采用了小波阈值降噪方法对原始信号进行了降噪[20],取得较好的降噪效果.
3.2 信号特征提取 3.2.1 基于GP算法的分形理论信号特征提取在1.3节中我们介绍了一种常用的关联维数算法,即GP算法.GP算法的几个关键参数为:重构相空间维数m、时间延迟τ和标量r.而在应用GP算法计算故障信号分形维数时,其参数的选取应遵守以下原则:
1) 假设原始信号的吸引子在d维空间中,则重构相空间维数m应满足:m≥2d+1.
2) 时间延迟τ的选择.若τ过小,得到的曲线会收敛于空间中的同一个方向;若取值过大,则相位图中会出现扭曲.本文采用Rosen-stein推荐值[21]: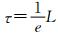
3) 标量r的范围.文献[22]中建议,为了确保分析结果的可靠性,取标量r上限值为使关联函数C(r) 的对数lnC(r) 近似为零的标量r取值;标量r的下限值为使求得的关联维数接近于相空间维数m时的标量r取值.
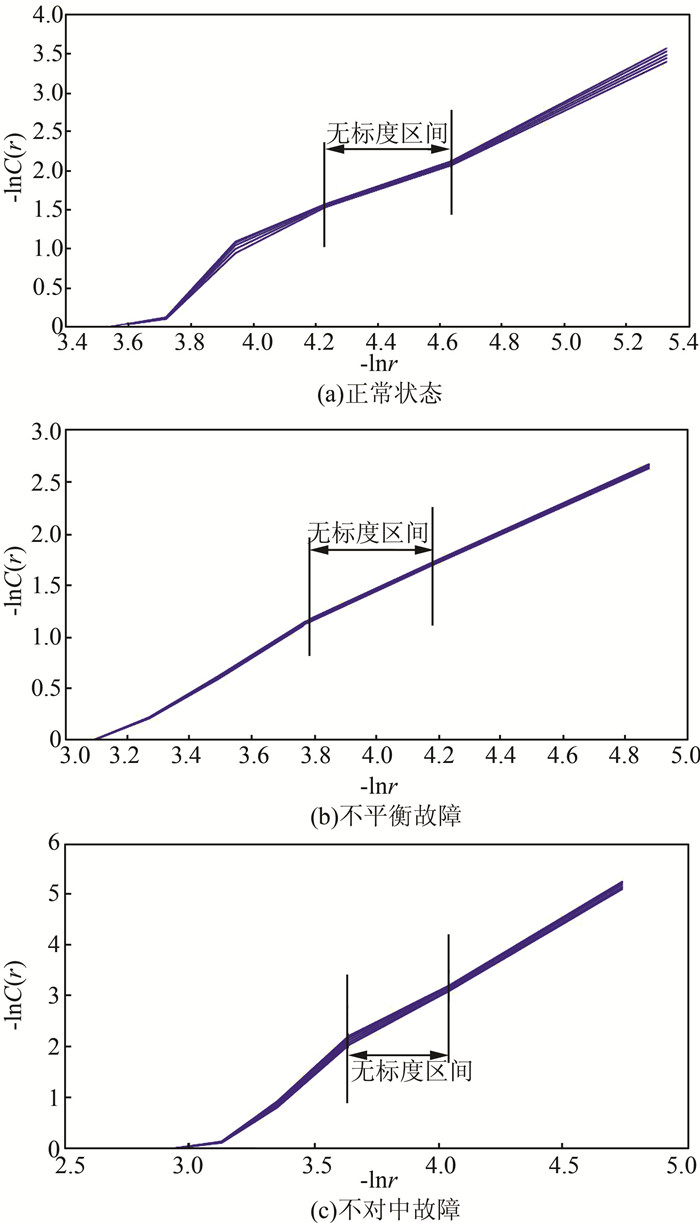
根据上面的原则,对各组实验数据利用GP算法进行了特征提取.图 4(a)~(c)展示了在不同工况下的双对数曲线,同时标注了对应的无标度区间.每张图中都有多条曲线,分别对应于不同的相空间维数m取值.尽管这些曲线互相并不重合,但是在无标度区间内的曲线段近似于直线且互相平行,即斜率相同,而其斜率即为所求的分形维数D.每种工况都有30组实验数据,实验结果见图 5.
|
| 图 4 不同工况下的双对数曲线 Figure 4 Double logarithm curves of different conditions |
|
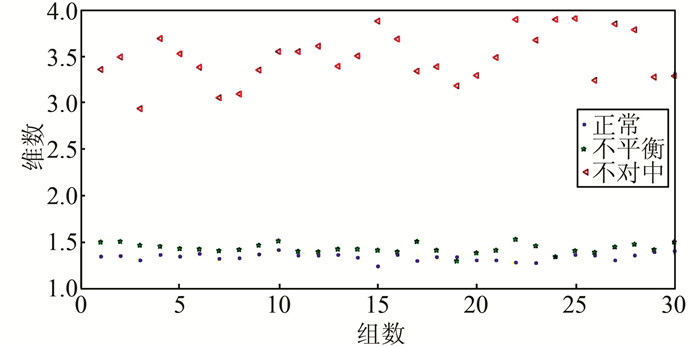
| 图 5 不同工况下基于GP算法得到的分形维数 Figure 5 Fractal dimension of different conditions using GP method |
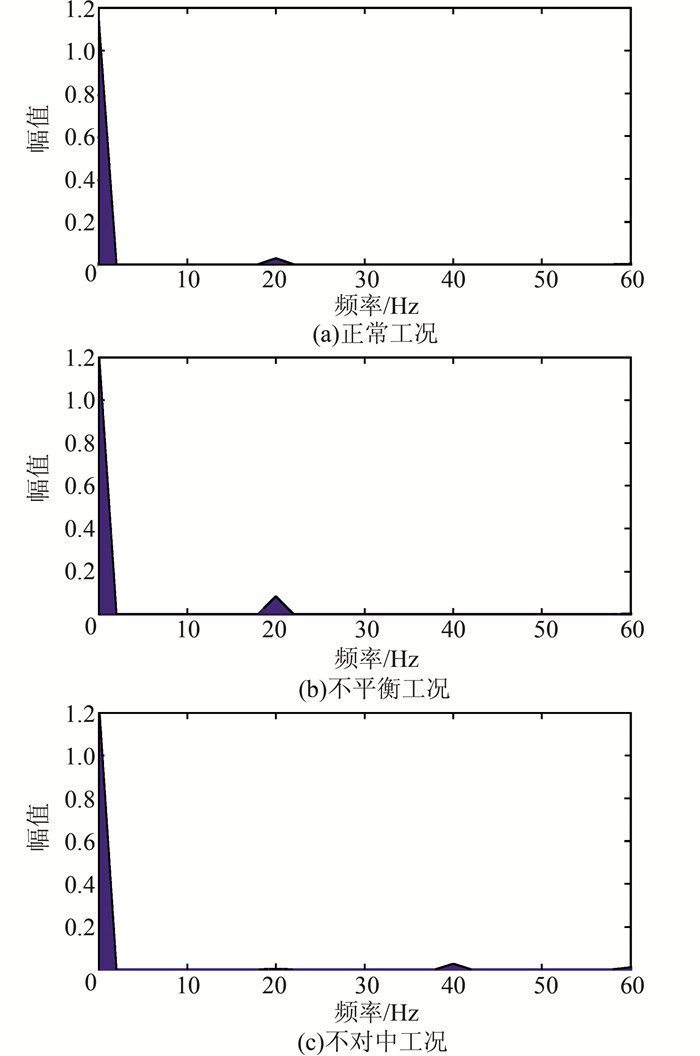
如图 3所示,实验得到不同工况下的数据并进行了降噪.转子试验台的转速设定为1 200 r/min,采样频率为2 048 Hz.为了更准确地选择本次算法所用到的小波函数,将用到各工况的功率谱 (如图 6所示) 以确定频带范围.为保证观察清晰性,超过200 Hz幅值接近于零的功率谱未示于图中.
|
| 图 6 不同工况下的功率谱 Figure 6 Power spectrum under different conditions |
表 1为采用Db家族小波对2 048 Hz的信号进行8层分解后,其各层对应的频率成分.对照机组各种状态下的功率谱图,可以发现,3种状态下的主要能量集中分布在0~60 Hz,参照表 1,利用Db小波家族进行信号分解后,其主要能量集中在第2~7层的细节成分中.经过小波分解后,各种状态下第2~7层的细节成分如图 7所示.
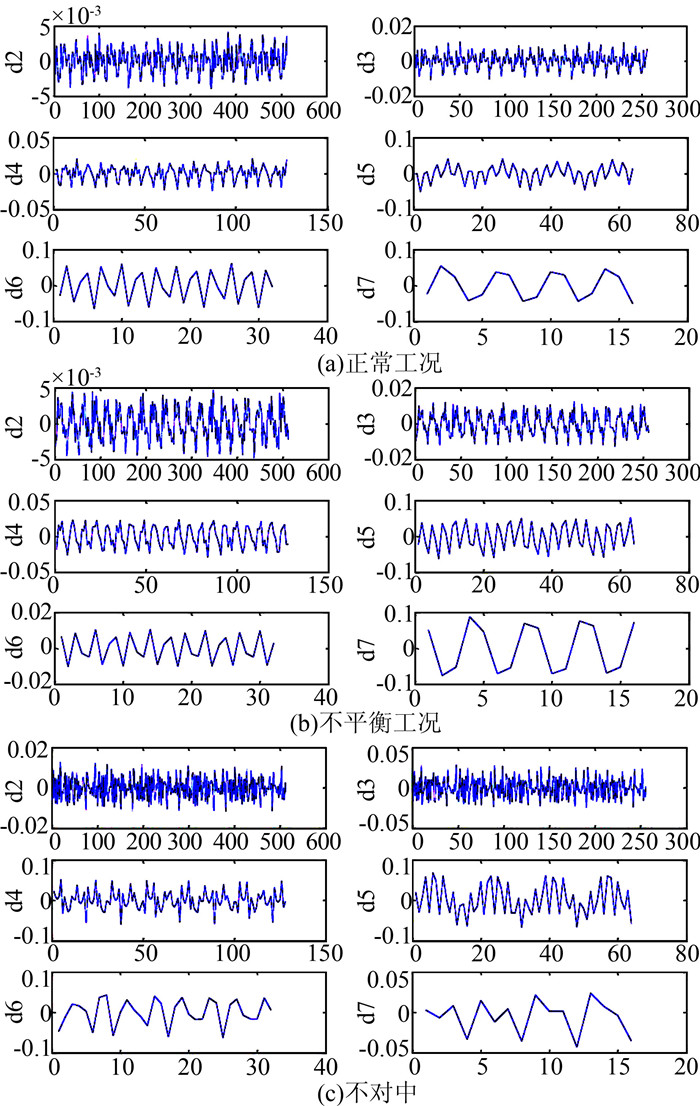
|
| 图 7 不同工况下信号分解后的细节成分 (第2~7层) Figure 7 Detail components (lever 2 to 7) under different conditions |
| 层 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频率 | 1 024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 |
| 范围 | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ~ |
| /Hz | 2 048 | 1 024 | 512 | 256 | 128 | 64 | 32 | 16 |
图 8(a)~(c)展示的是各工况下以尺度j为横轴、Var (d2j) 为纵轴所得的拟合直线.
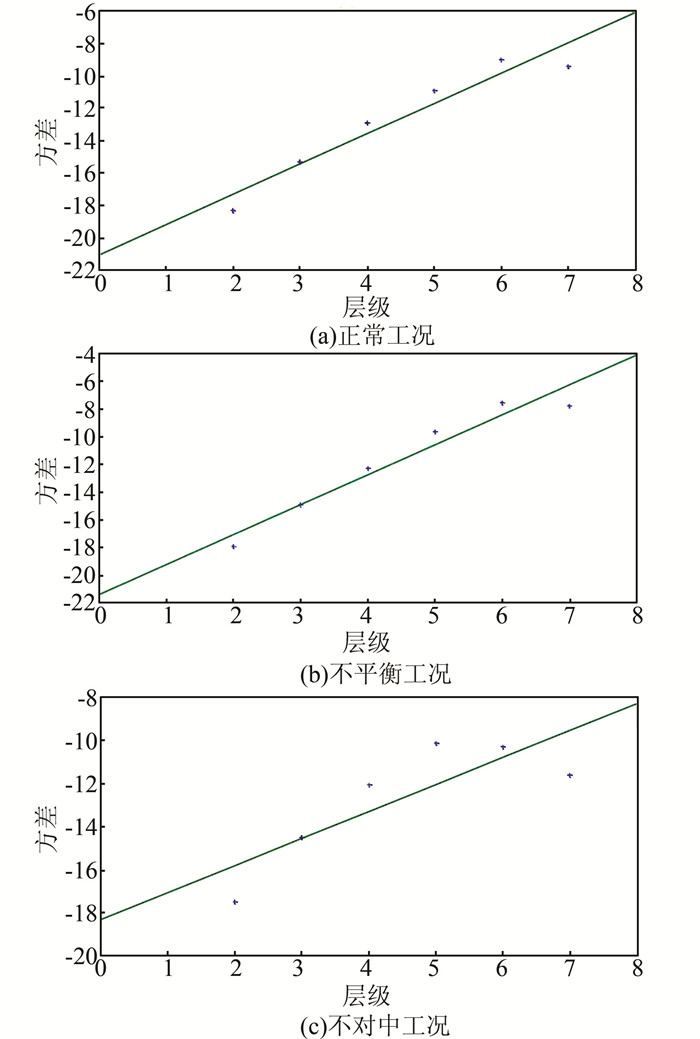
|
| 图 8 各工况下的拟合直线 Figure 8 Fitting lines under different conditions |
每种工况下都有30组数据,将降噪信号作为输入信号,经过小波分形算法提取特征后,得到各工况下的分形维数如图 9所示.
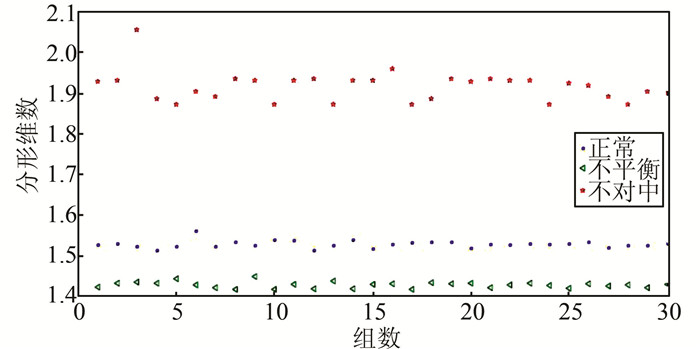
|
| 图 9 不同工况下基于小波分形算法的分形维数 Figure 9 Fractal dimension of different conditions using wavelet fractal algorithm |
图 5和图 9分别为传统关联维数算法和本文提出的小波分形算法的特征提取结果.从图中可以看出2种方法所提取的分形维数都有较好的效果,能较为清晰地分辨3种不同工况.图 5中,结果曲线较为杂乱且在正常状态和不平衡工况的分形维数曲线间有重合;而图 9中,各工况分形维数曲线间并无重合且边界更为清晰,说明识别准确率更高.对不同算法不同工况下的30组分形维数进行了统计学分析,得到结果如表 2所示.
| 工况 | GP算法 | 小波分形算法 | |||
| 均值 | 标准差 | 均值 | 标准差 | ||
| 正常 | 1.326 7 | 0.037 9 | 1.528 6 | 0.008 90 | |
| 不平衡 | 1.418 4 | 0.052 0 | 1.428 0 | 0.007 49 | |
| 不对中 | 3.484 0 | 0.261 0 | 1.916 3 | 0.036 60 | |
从表 2中可知,即使是同一工况下,2种方法得到的分形维数的均值也不同,其原因在于2种方法本质有区别.GP算法计算的是信号的绝对分形维数,而小波分形算法的本质则是考察不同尺度下能量分配的相对值,也即是功率谱在不同频段内的相对分配.因此,小波分形算法得到的分形维数是一个相对值.由表 2也可以看出,在各工况下小波分形算法的标准差较之GP算法都要小一个数量级,也就是说,小波分形算法得到的分形维数更为稳定、集中,具有更高的准确性.
4 结论近年来,随着分形理论的迅速发展,其在包括旋转机械的故障诊断领域有了较多应用.然而,由于分形理论对信号的研究并不包括信号细节成分的分析,因此可能引起故障诊断偏差.本文提出了一种基于小波分形算法的旋转机械故障特征提取算法,该算法将小波函数和分形维数两种重要的故障诊断工具结合起来,既考虑信号细节成分,同时也注重了其局部与整体的关系,因此更加准确.本文利用转子试验台模拟了3种工况下的水轮机组振动信号,并分别用传统分形维数算法和本文提出的小波分形算法进行了特征提取.结果表明,两种算法均有良好效果,但小波分形算法具有较高的准确性,为准确提取旋转机械振动信号故障特征提供了一种快速有效的新方法.
| [1] |
梁武科, 张彦宁, 罗兴锜. 水电机组故障诊断系统信号特征的提取[J].
大电机技术, 2003(4): 53–56.
Liang Wuke, Zhang Yanning, Luo Xingqi. Characteristic pickup of hydroelectric set fault diagnose system[J]. Mechanical & Electrical Technology, 2003(4): 53–56. |
| [2] | Howard C Chloe, Clark E Poole, Andrea M Yu, et al. Novel identification of intercepted signals from unknown radio transmitters[J]. Proceedings of the SPIE, 1995(4): 504–517. |
| [3] | Yang D M, Stomach A F, MacDonnell P, et al. Third-order spectral techniques for the diagnosis of motor bearing condition using artificial neural networks[J]. Mechanical Systems and Signal Processing, 2002(16): 391–411. |
| [4] | James A Leonard, Mark A Kramer. Radial basis function networks for classifying process faults[J]. IEEE Control Systems, 1991, 11(3): 31–38. DOI:10.1109/37.75576 |
| [5] | Mo Yuen Chow, Robert N Sharpe, James C Hung. On the application and design of artificial neural networks for motor fault detection[J]. IEEE Transactions on Industrial Electronics, 1993, 40(2): 181–196. DOI:10.1109/41.222639 |
| [6] | Larry P Heck, Chou K C. Gaussian mixture model classifiers for machine monitoring[J]. IEEE Acoustics Speech and Signal Processing, 1994(7): 4493–4496. |
| [7] |
赵道利, 梁武科, 罗兴琦, 等. 水电机组振动信号的子带能量特征提取方法研究[J].
水力发电学报, 2004(6): 116–119.
Zhao Daoli, Liang Wuke, Luo Xingqi, et al. On sub-band energy feature extraction method of vibration fault signals of hydroelectric sets[J]. Journal of Hydroelectric Engineering, 2004(6): 116–119. |
| [8] |
马晋, 江志农, 高金吉. 基于混沌分形理论的特征提取技术在气阀故障诊断中的应用[J].
振动与冲击, 2012, 31(19): 26–30.
Ma Jin, Jiang Zhinong, Gao Jinji. Feature extraction method based on chaotic fractal theory and its application in fault diagnosis of gas valves[J]. Journal of Vibration and Shock, 2012, 31(19): 26–30. |
| [9] | Jiang Y J, Tanabashi Y, Xiao J. Relationship between surface fractal characteristic and hydro-mechanical be havior of rock joints[C]// Proceedings of the ISRM International Symposium third ARMS, 2004, 2:833-843. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201219009.htm |
| [10] |
刘雨佳.滑动轴承声发射信号形态滤波及分形特征提取方法[D].长沙:长沙理工大学, 2013:13-17.
Liu Yujia. Morphological filtering and fractal features extraction method for acoustic emission signals of journal bearings[D]. Changsha: Changsha University of Science and Technology, 2013:13-17. |
| [11] |
黄伟国.基于振动信号特征提取与表达的旋转机械状态监测与故障诊断研究[D].合肥:中国科学技术大学, 2010: 21-30.
Huang Weiguo. Research on feature extraction and representation with vibration signal for rotary machinery condition monitoring and fault diagnosis[D]. Hefei: University of Science and Technology of China, 2010: 21-30. |
| [12] |
张济忠.
分形[M]. 北京: 清华大学出版社, 1997: 112-114.
Zhang Jizhong. Fractal[M]. Beijing: Tsinghua University Press, 1997: 112-114. |
| [13] |
董连科.
分形理论及其应用[M]. 沈阳: 辽宁科学技术出版社, 1991: 214-215.
Dong Lianke. Fractal Theory and Its Application[M]. Shenyang: Liaoning Science and Technology Press, 1991: 214-215. |
| [14] | Peter Grasberg, Tamar Privacies. Measuring the strangeness of strange attractors[J]. Physica D, 1983, 9: 189–208. DOI:10.1016/0167-2789(83)90298-1 |
| [15] |
刘式达, 刘式适.
分形与分维引论[M]. 北京: 气象出版社, 1992: 45-48.
Liu Shida, Liu Shishi. An Introduction to the Fractal and Fractal Dimension[M]. Beijing: China Meteorological Press, 1992: 45-48. |
| [16] | Donohue D L, Johnston I M. Adapting to unknown smoothness via wavelet shrinkage[J]. J ASA, 1995, 90: 1200–1223. |
| [17] | Wornell G W, Oppenheim A V. Estimation of fractal signals from noisy measurements using wavelets[J]. IEEE Trans Signal Proc, 1992, 40: 611–623. DOI:10.1109/78.120804 |
| [18] | Flandrin P. On the spectrum of fractional Brownian motions[J]. IEEE Trans Inform Theory, 1989, 35: 197–199. DOI:10.1109/18.42195 |
| [19] | Flandrin P. Wavelet analysis and synthesis of fractal Brownian motions[J]. IEEE Trans Inform Theory, 1992, 38(2): 910–917. DOI:10.1109/18.119751 |
| [20] |
苏立, 南海鹏, 余向阳, 等. 基于改进阈值函数的小波降噪分析在水电机组振动信号中的应用[J].
水力发电学报, 2012(3): 246–251.
Su Li, Nan Haipeng, Yu Xiangyang, et al. Application of wavelet denoising of improved threshold function to vibration signal analysis of hydroelectric units[J]. Journal of Hydroelectric Engineeriong, 2012(3): 246–251. |
| [21] |
党建武, 黄建国. 基于GP算法的关联维计算中参数取值的研究[J].
计算机应用研究, 2004(1): 48–51.
Dang Jianwu, Huang Jianguo. Study of the parameters used in calculating correlative dimension based on GP algorithm[J]. Application Research of Computers, 2004(1): 48–51. |
| [22] |
施泽进, 李忠权, 应丹琳. 序列数据关联维的计算及意义[J].
成都理工学院学报, 1996, 23(2): 88–92.
Shi Zejin, Li Zhongquan, Ying Danlin. Correlation dimensional calculation of series data and its significance[J]. Journal of Chengdu Institute of Technology, 1996, 23(2): 88–92. |
 2017, Vol. 50
2017, Vol. 50




