文章信息
- 别丽华, 蒋天发, 李倩, 周晋
- BIE Lihua, JIANG Tianfa, LI Qian, ZHOU Jin
- 基于Hash table的启发式A-star及其改进算法在最短路径问题中的高效实现
- Design and implementation of heuristic A-star algorithm on shortest path problem based on Hash table
- 武汉大学学报(工学版), 2016, 49(6): 944-948
- Engineering Journal of Wuhan University, 2016, 49(6): 944-948
- http://dx.doi.org/10.14188/j.1671-8844.2016-06-024
-
文章历史
- 收稿日期: 2015-12-25
2. 武汉理工大学华夏学院,湖北 武汉 430223;
3. 杭州四方博瑞数字电力科技有限公司,浙江 杭州 310030
2. Huaxia College, Wuhan University of Technology, Wuhan 430223,China;
3. Hangzhou Sifang Borui Digital Power Technology Co., Ltd., Hangzhou 310030,China
基于位置的服务(location-based services,LBS)集成了应用空间信息技术和移动通信技术,可为出行者提供路径导引服务[1].路径规划功能是实现此服务的核心功能之一,其合理性和效率直接影响到服务的质量,而路径规划的问题实质上就是最优(最快、最短、最低费用)路径问题[2].常用的路径搜索算法有Dijkstra 算法[3]、Bellman Ford 算法、Floyd-Warshall算法和A-star等算法[4],其中启发式A-star算法在路径寻优过程中通过启发函数计算选择代价最少的节点,计算简单、算法易实现,并且在理论上可以保证全局最优解的收敛性,因此得到了广泛的应用.
大多数对于启发式A-star算法的研究和改进,往往关注算法中评估函数的优化、改良,而对算法实现的核心数据结构关注度不够,传统方法中多半采用数组、链表来实现数据结构,由于要为出行者提供路径导引服务时需要存储、处理海量的路网节点信息,并进行频繁的插入和查找等操作,采用数组模式
会占用大量的内存,需要频繁进行磁盘IO操作,而链表模式的查找检索时间又过长,从而造成启发式A-star算法整体效率不高,运行缓慢.本文基于哈希表能提供快速增删和查找内部节点数据的优点,将哈希表应用于启发式A-star算法中,从而加快数据存储、访问的速度,进一步提升算法效率,优化路径规划的搜索效率.
1 启发式A-star算法原理Hart等人于1971年提出的启发式A-star算法[5]是一种重要的最优路径搜索的方法.所谓启发式搜索就是利用知识来引导搜索,减少搜索范围,从而降低问题的复杂度[6].目前A-star算法已广泛应用于实时系统、人工智能等多种领域.在算法搜索过程中,每个被评估节点n被赋予权重,从起点开始对每一个能直接到达的节点进行搜索评估,选择其中代价最少的结点作为下一个位置,再从当前位置开始进行搜索得到下一个最好位置,重复此过程直至到达目标位置.在A-star算法中评估函数的一般形式为
其中:f(n)指的是从起点经由节点n到目标节点的评估函数;g(n)指从起点到节点n的最短路长,可以根据已计算的节点路长属性和节点n自身路长属性,得出起点到节点n路长总值;h(n)也叫启发函数,指节点n到目的地最小路长估计.根据f(n)的计算结果大小确定下一搜索位置直至终点.
静态交通中的最短路径问题常用的h(n)函数常用曼哈顿距离或欧几里德距离等来表示[7],因欧几里德距离具有平面坐标轴平移和旋转后的不变性,并且估算精度较高,本文也是基于欧几里德距离转变方法进行具体h(n)应用估算,具体公式为
在A-star算法的实现过程中,一般需要构造两个表:open表和close表.open表用于存放已经被计算但还没有被扩展的节点,close表用于存放已经被扩展的节点.在每一步的搜索过程中,首先从open表中找出代价值最小的节点,将其加入close表进行扩展,对扩展后的节点进行分析,根据分析结果对open表和close表进行修改,选择合适的扩展节点加入close表.
由于A-star算法在每一步的搜索过程中并不确定最终的路径,它需要对每一个节点进行搜索和评估,并且存储中间值,以便最后选取最优路径,故而当节点数量较大的情况下会耗费大量的资源,降低计算的速度,使算法的效率降低.在启发式搜索中,对下一位置的权重评估是非常关键的,采用不同的评估函数得到的效果也是有差异的.文献[8]就是通过优化评估函数来提高算法效率的.在搜索的实现中,主要的搜索和比较都在open表和close表中完成,故而这两张表选取何种数据结构是一个非常关键的问题,通用的方法是采用数组、链表或堆栈,数组便于对数据进行存取,但是插入和删除操作会带来大量的时间开销,链表的插入和删除操作虽然简单但是对数据的定位仍需借助搜索[9],通过改进数据结构提高搜索效率以用于工程实现的研究并不多见,文献[10]设计了装箱式数据结构管理close表,提高了对重复节点的查找效率,采用最小二叉树的方式管理open表,提高了算法的搜索效率.
针对静态交通中的最短路径问题,需要在海量的路网节点数据中迅速检索匹配到相应的节点,本文主要从优化数据结构的角度提出采用哈希表来实现open表和close表数据的存储和快速查找,经实际应用验证了其正确性和高效可行性.
2 哈希表的快速检索原理 2.1 哈希表描述哈希表(Hash table,也叫散列表),是通过设定的函数f(key)和处理冲突的方法将一组关键字key映像到一个有限的连续的地址集上,并以关键字在地址集中的“像”作为记录在表中的存储位置,具体公式为
这个对应关系f(key)称为哈希(Hash)函数.也就是说,它通过把关键码值映射到表中的一个位置来访问记录,以加快查找的速度,简单而实用.文献[11]中还从存储结构、多步划分和数据倾斜等3个方面来优化哈希划分,得到了较好的效果.
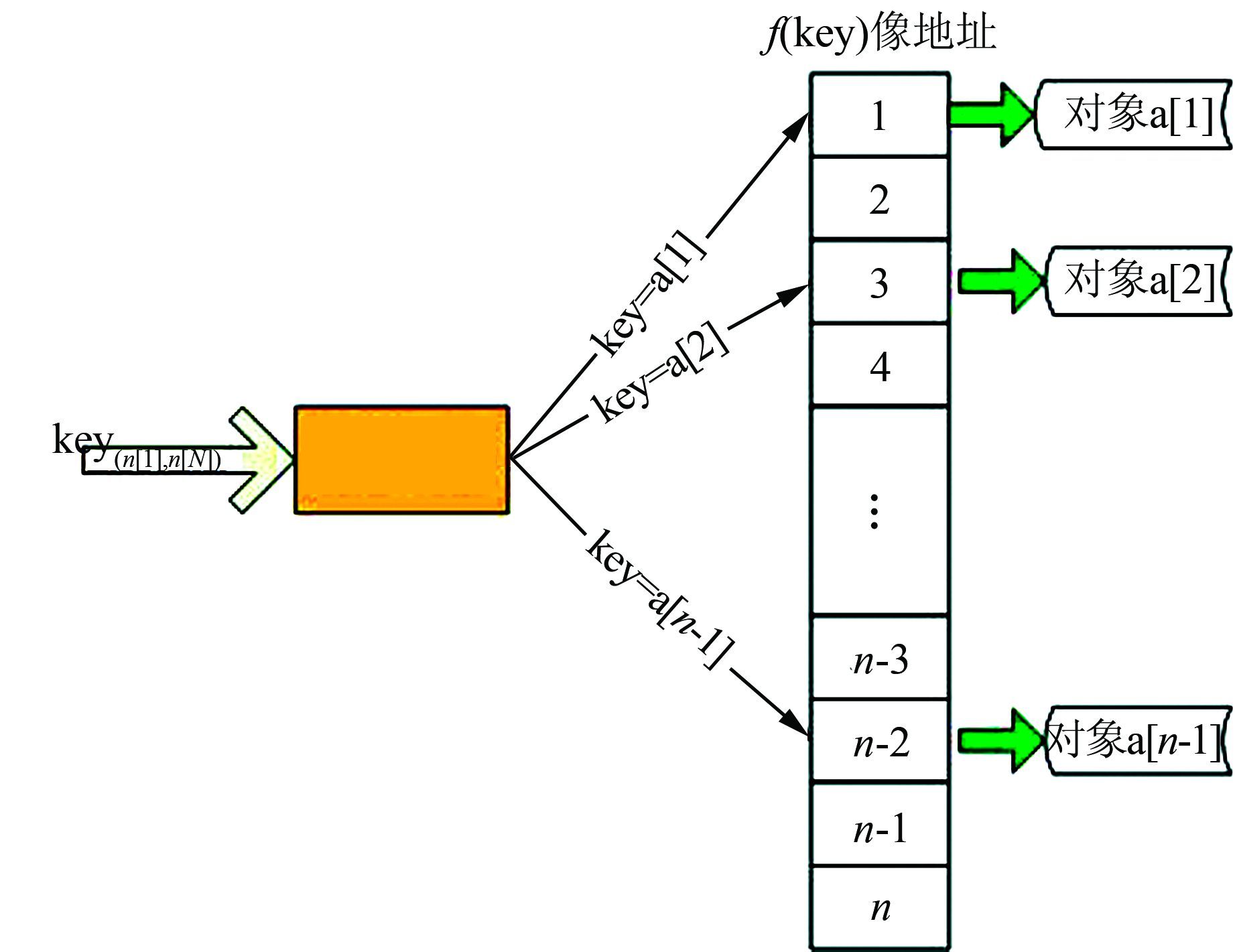
2.2 快速检索原理本文需要在海量的路网节点数据中迅速检索匹配到相对应的节点,避免比较,一次存取便能得到所查记录,必须在记录的存储位置和它的检索关键字之间建立一个确定的对应关系f,使每个关键字与结构中一个唯一的存储位置相对应.在查找时,只需根据对应关系f便能找到给定值key的像f(key).若结构中存在关键字和key相等的记录,则必定在f(key)的存储位置上,由此,不需要进行比较便可直接取得所查纪录.
如图 1所示,哈希表的检索是根据对应关系f找到给定值key的像f(key),若结构中存在和关键字相等的记录,且必定在f(key)的存储地址上,则这个对应关系f即为哈希(Hash)函数.但是对不同key可能得到同一散列地址,即key1≠key2,而f(key1)=f(key2),这种现象称为冲突.冲突的出现将影响搜索数据的效率,目前常用的解决冲突的方法有开放地址法、再散列法等,但是都会付出存储空间或查找时间的代价.
|
| 图 1 哈希表的检索原理 Figure 1 Search principle of Hash table |
为更加有效地利用哈希表快速检索、映射的特性,并避免不必要冲突的出现,本文从源头路网数据检索关键字key设计开始,利用一维对象容器的数据结构,通过转换关系f生成路网数据关键字key的值,并自动重新生成产生冲突的key值,避免不必要的检索时间、空间浪费.将生成的无冲突源路网数据通过f(key)转换到容器对象地址进行存储,检索算法的时间复杂度在0(1),能最有效地保证数据查询、获取的速度.
2.3 算法改进[12-14]本文的算法实现暂以一个省的路网为具体测试数据,其中的数据结构的规划设计可以扩展到全国路网.
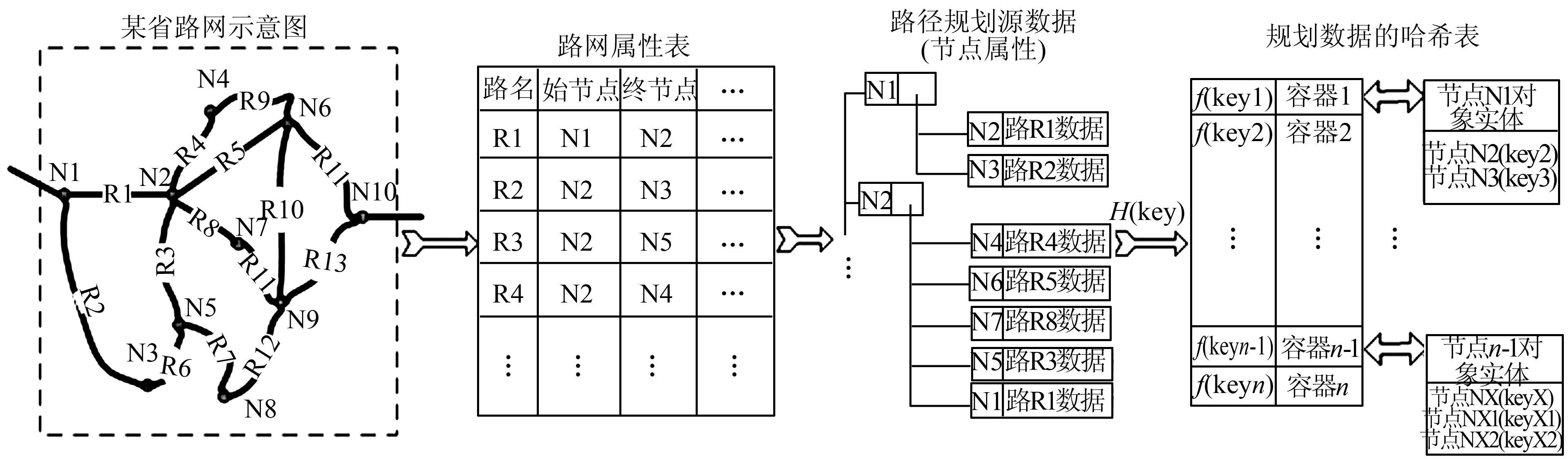
如图 2所示,全省的路网数据被分割成一条条线路,每条线路都在路网属性表中对应着一条线路属性记录,包括该线路的路名、始节点和终结点等信息.本算法根据路网的数据特性,首先从路网属性表中抽象出各个始节点类及对应的唯一节点索引属性(省编码+市编码+道路等级编码+等级流水号编码),始节点类中包含着与始节点之间连接的所有终节点索引属性信息,然后将该始节点的索引键与始节点类存储到Hash table里面,构成最初的规划节点数据.把路网数据转换成规划节点数据后,根据key=省编码+市编码+道路等级编码+等级流水号编码形成规划节点数据的检索主键,即节点索引属性.故哈希函数
将式(4)作为数据检索公式,根据规整后的规划节点数据生成规划节点Hash table.
|
| 图 2 矢量路网数据生成规划哈希表 Figure 2 Vector data of road network to generate Hash table |
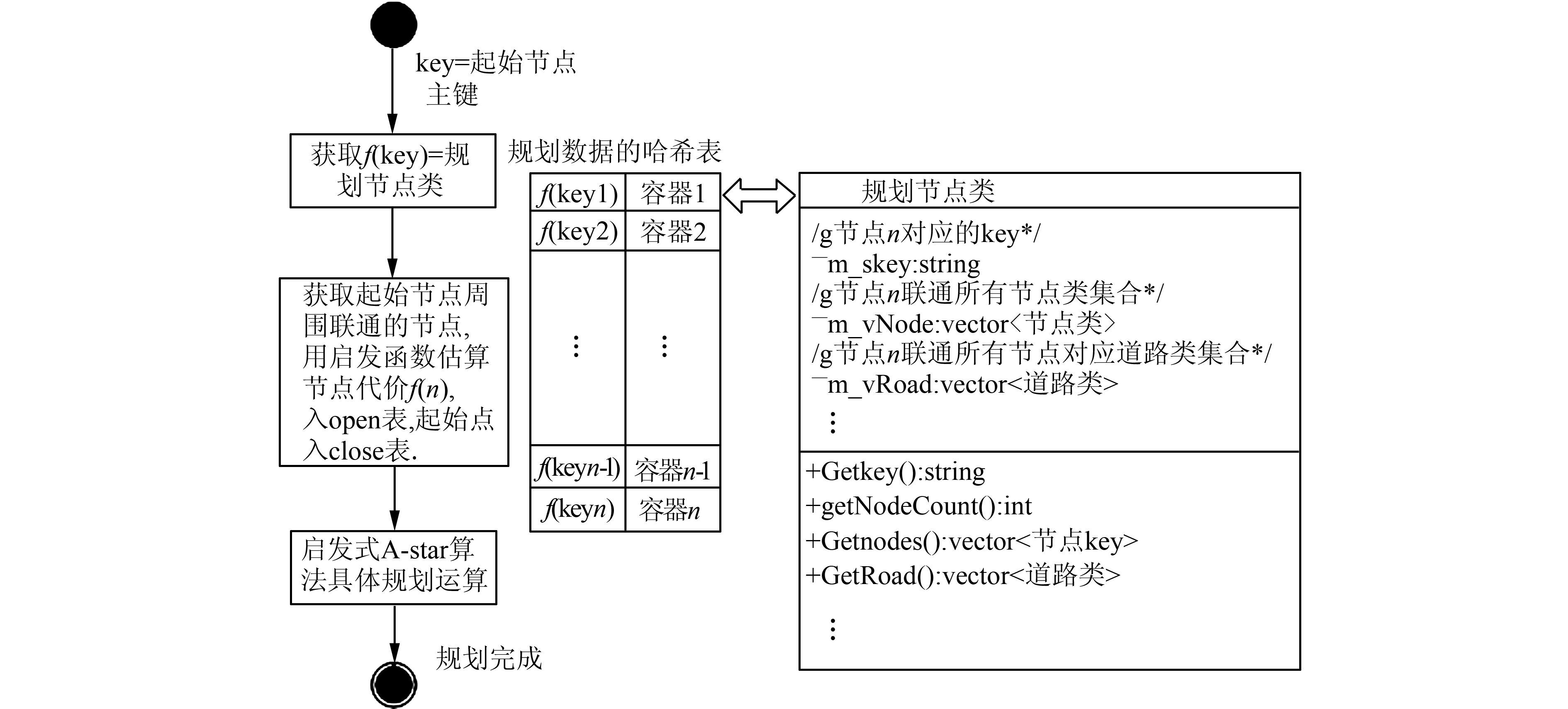
基于以上规划路网节点的数据结构,每个节点数据包括了周围联通节点集合与对应的道路集合,假定起点和终点的f(key)都在规划数据的哈希表中,具体改进启发式A-star算法如图 3所示.
|
| 图 3 基于Hash table的路网数据组织 Figure 3 Data organization of road network based on Hash table |
1) 根据要规划路径起始节点的key值从规划节点Hash table中快速获取规划节点类,将该节点可以连通的节点通过f(n)=g(n)+h(n)计算估价值并放入open表中,起点本身放close表中.
2) 从open表中取估价值最小的节点n,判断如果是终点,即可结束寻路,根据上级索引节点信息即可生成搜寻到的路径.
3) 遍历节点n周围所有结点x并计算f(x)值.
4) 节点x在open表中,如果x新的f(x)值小于旧的f(x)值则更新open表x对应的value值,
如果x在close表中,并且新的f(x)值小于旧的f(x)值则更新close表,并且将x插入open表.如果x既不在open表也不在close表中,则直接插入open表.
5) 把n结点从open表中取出,放入close表中.
6) 根据估值将open表中的所有节点排序,使f值最低的结点排在最前面.
7) 返回重新执行第二步直到找到终点,或者open表为空,说明没有路径可以到达终点.
3 仿真与分析本文采用湖北省近期导航数据作为算法实验数据,全省路网有48 133条,路网节点数据1 683 085个,采用直线距离10、30、50 km 3组试验数据来比较传统的链表模式和本文提出的Hash table方法的效率,结果如表 1所示.
| 实验序列 | 规划路径长度/km | 搜索节点数 | 比较方式 | 时间/ms | 优化幅度/% |
| 1 | 10 | 4 816 | 传统算法 | 2856 | 29 |
| 改进算法 | 2021 | ||||
| 2 | 30 | 13 214 | 传统算法 | 9 871 | 33 |
| 改进算法 | 6 621 | ||||
| 3 | 50 | 36 921 | 传统算法 | 21 956 | 44 |
| 改进算法 | 12 291 |
从试验结果来看,改进后的启发式A-star算法比传统的算法运算速度更快,并能为后续静态交通中的路径规划服务奠定良好的基础.
4 结束语本文基于哈希表来存储、管理和检索路网数据,保证了启发式A-star算法应用效率的最优,获得了更好的路径规划实现.将该算法应用到全省路网数据中进行路径规划试验,证明本算法在改进启发式A-star算法执行效率方面具有良好的效果.本文提出的改进方法不仅能在单机的路径规划中大幅提高路网数据的查找、检索速度,而且可以在分布式计算中将各省的路网哈希表进行无缝联通,实现全国路网的分布式路径规划服务,为后期进一步的应用和深入研究奠定了基础.
| [1] |
李清泉, 郑年波, 徐敬海, 等. 一种基于道路网络层次拓扑结构的分层路径规划算法[J].
中国图像图形学报, 2007, 12(7): 1280–1285.
Li Qingquan, Zhen Nianbo, Xu Jinghai, et al. A hierarchy path planning algorithm based on road network topology structure[J]. Journal of Image and Graphics, 2007, 12(7): 1280–1285. |
| [2] |
乐阳, 龚健雅. Dijkstra最短路径算法的一种高效率实现[J].
武汉测绘科技大学学报, 1999, 24(3): 209–212.
Yue Yang, Gong Jianya. An efficient implementation of Dijkstra shortest path algorithm[J]. Geomatics and Information Science of Wuhan University, 1999, 24(3): 209–212. |
| [3] |
邓谱, 彭玺, 田立峰, 等. 一种基于连通度的电力信息网络生存性分析方法[J].
武汉大学学报(工学版), 2010, 43(6): 792–795.
Deng Pu, Peng Xi, Tian Lifeng, et al. An analysis method on survivability of electric power information network based on connectivity[J]. Engineering Journal of Wuhan University, 2010, 43(6): 792–795. |
| [4] |
王树西, 吴政学. 改进的Dijkstra最短路径算法及其应用研究[J].
计算机科学, 2012, 39(5): 223–227.
Wang Shuxi, Wu Zhengxue. An improved Dijkstra shortest path algorithm and its application research[J]. Computer Science, 2012, 39(5): 223–227. |
| [5] | Hartpe Nilsson N J, Raphael B. A formal basis for the heuristic determination of minimum cost paths in graphs[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, SSC-4(2): 100–107. |
| [6] |
林笃斌, 李欣. 基于DEM 格网的改进型A*路径搜索算法[J].
计算机工程与设计, 2011, 32(10): 3414–3418.
Lin Dubin, Li Xin. An improved A* path search algorithm based DEM grid[J]. Computer Engineering & Design, 2011, 32(10): 3414–3418. |
| [7] |
孟中杰, 黄攀峰, 阎杰. 基于改进稀疏A*算法的高超声速飞行器航迹规划技术[J].
西北工业大学学报, 2010, 28(2): 182–186.
Meng Zhongjie, Huang Panfeng, Yan Jie. Flight path planning technology for hypersonic vehicle based on an improved sparse A* algorithm[J]. Journal of Northwestern Polytechnical University, 2010, 28(2): 182–186. |
| [8] |
张林, 米雪玉, 王彬. 基于交通信息时效性的车辆路径优化方法[J].
交通工程, 2014(6): 392–394.
Zhang Lin, Mi Xueyu, Wang Bin. Vehicle routing optimization method based on traffic information timeliness[J]. Traffic Engineering, 2014(6): 392–394. |
| [9] |
李季, 孙秀霞. 基于改进A-star算法的无人机航迹规划算法研究[J].
兵工学报, 2008, 29(7): 788–792.
Li Ji, Sun Xiuxia. Research on UAV flight path planning algorithm based on improved A-star algorithm[J]. Acta Armamentarii, 2008, 29(7): 788–792. |
| [10] |
任上, 秦江涛. 基于着色Petri网实现A*算法的生产调度优化研究[J].
上海理工大学学报, 2013, 35(5): 463–474.
Ren Shang, Qin Jiangtao. Research on implement of A-star algorithm of production scheduling optimization based on a colored Petri networks[J]. Journal of University of Shanghai for Science and Technology, 2013, 35(5): 463–474. |
| [11] |
杨楠, 张健. 启发式最优航迹规划算法数据结构的改进研究[J].
计算机应用研究, 2011, 28(8): 2919–2921.
Yang Nan, Zhang Jian. Improvement and research on the data structure of heuristic optimal route planning algorithm[J]. Application Research of Computers, 2011, 28(8): 2919–2921. |
| [12] |
袁通, 刘志镜, 刘慧, 等. 多核处理器中基于Mapreduce的哈希划分优化[J].
西安交通大学学报, 2014, 48(11): 97–102.
Yuan Tong, Liu Zhijing, Liu Hui, et al. Hash partitioning optimization of multi-core processor based on Mapreduce[J]. Journal of Xi'an Jiaotong University, 2014, 48(11): 97–102. |
| [13] |
肖自兵, 袁冬莉, 屈耀红. 基于A*定长搜索算法的多无人机协同航迹规划[J].
飞行力学, 2012, 30(1): 92–96.
Xiao Zibing, Yuan Dongli, Qu Yaohong. Unmanned aerial vehicle cooperative path planning based on A* fixed-length search algorithm[J]. Flight Dynamics, 2012, 30(1): 92–96. |
| [14] | Dai Zhiquan, Guan Yong, Guan Ran. Dynamic adjustment A* routing algorithm[C]// Proceedings of CICC-ITOE 2010 International Conference on Innovative Computing and Communication. |
| [15] | Zhang Jing, Li Xia, Chen Jian, Qian Zhilei. Multi-core BDD operations for symbolic reachability electronic[J]. Theoretical Computer Science, 2013(296): 325–328. |
 2016, Vol. 49
2016, Vol. 49




