文章信息
- 邵克博, 曹子君, 李典庆
- SHAO Kebo, CAO Zijun, LI Dianqing
- 基于子集模拟的浅基础扩展可靠度设计
- Efficient reliability-based design of shallow foundation using subset simulation
- 武汉大学学报(工学版), 2017, 50(4): 517-525
- Engineering Journal of Wuhan University, 2017, 50(4): 517-525
- http://dx.doi.org/10.14188/j.1671-8844.2017-04-006
-
文章历史
- 收稿日期: 2016-12-15
2. 武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072
2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering, Ministry of Education, Wuhan University, Wuhan 430072, China
基础工程可靠度设计方法为合理地考虑岩土工程中多种不确定性因素(如参数不确定性和模型不确定性)对基础设计的影响提供了一条科学、有效的途径.近年来,基于可靠度理论的基础设计方法受到越来越多的关注,世界上多个国家和地区逐步拟定了可靠度设计规范,如加拿大的国家建筑规范基础部分[1]、日本的岩土工程可靠度设计规范Geocode21[2]以及欧洲可靠度设计规范Eurocode7[3, 4].这些规范基于既定的目标可靠度指标βT对荷载、抗力或材料分项系数进行标定,并在标定过程中需要假设基础承载能力极限状态(ultimate limit state, ULS)和正常使用极限状态(serviceability limit state, SLS)的功能函数以及岩土体参数的概率分布特征(包括分布类型、统计特征等).然而,通常情况下工程师对这些假设并不了解,也无法根据现场的实际情况调整这些假设,只能接受这种假设,并在设计中直接采用对应的分项系数.这种做法容易导致误用不合适的分项系数,导致最终设计不能满足设计要求所对应的目标可靠度指标βT.
为了解决上述问题,Wang等[5]提出了一种基于直接蒙特卡洛模拟(Monte Carlo simulation, MCS)的扩展可靠度设计方法(expanded reliability-based design, Expanded-RBD).该方法允许工程师根据工程现场实际情况、试验数据以及相应的工程经验确定合适的确定性分析方法(或功能函数)、岩土体参数概率分布特征以及目标可靠度指标.尽管扩展可靠度设计方法通过利用直接MCS模拟,使其概念以及计算都得到了充分简化,但是工程实践中所关心的设计区域对应的失效概率Pf较小(比如Pf<0.001),直接MCS模拟在小概率失效空间内计算效率非常低[6].这一缺点直接阻碍了Expanded-RBD方法在基础工程实践中的应用.为此,Wang和Cao[7]尝试将一种高效的蒙特卡洛模拟方法——子集模拟(subset simulation,SS)应用到Expanded-RBD中,提高其在小概率失效空间的设计效率,他们指出SS和Expanded-RBD的联合十分困难,其关键在于如何在SS中构造一个合适的系统响应量.
本文基于SS提出了一种新的扩展可靠度浅基础设计方法,建立一个具有广泛适用性的代理系统响应量.为了提高所提出方法的实用性,本文基于Visual Basic Application(VBA)和EXCEL表单环境编写了计算程序和用户界面.将可靠度分析与计算、确定性分析模型和不确定性分析模型分别采用相对独立的模块实现,使设计过程相对清晰明了,简单易行.最后,通过一个浅基础算例,将提出的方法加以说明和应用,并将设计结果与文献中的研究成果进行对比,说明了所提出方法和程序的适用性、准确性和实用性.
1 浅基础扩展可靠度设计方法浅基础可靠度设计的目标是确定一组合适的设计参数(包括基础的宽度B、长度L和深度D)来满足ULS和SLS对应的目标可靠度水平(即目标可靠度指标βTULS和βTSLS或目标失效概率pTULS和pTSLS).在扩展可靠度设计方法中,采用离散型均匀分布的随机变量表征浅基础的设计参数B、L和D.设计参数的每个组合代表了设计空间中的一个可能的设计方案.浅基础的设计过程进而转化为计算各个设计方案对应的条件失效概率P(F|B, L, D),并将其与目标失效概率pTULS和pTSLS做对比,选择可行设计方案的过程.可行设计方案的条件失效概率P(F|B, L, D)应小于或等于pTULS和pTSLS中的较小值.根据贝叶斯原理,条件失效概率P(F|B, L, D) [5, 7-8]可以通过下式进行计算:
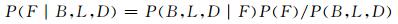 (1)
(1)
式中:P(B, L, D|F)为失效条件下设计参数组合B、L和D的联合概率分布;P(B, L, D)= 1/(nB×nL×nD),其中nB、nL和nD分别为设计空间中设计参数B、L和D可能值的数目;P(F)=失效样本数与总样本数之比.其中P(B, L, D)和P(F)可以通过直接MCS模拟进行估计.当目标失效概率较小时(比如pT<0.001),采用直接MCS模拟所需要的样本数巨大,计算效率低[5, 7].为了提高设计效率,在下一节中本文将会采用一种高效的MCS模拟方法——子集模拟(SS)估计P(B, L, D|F)和P(F).
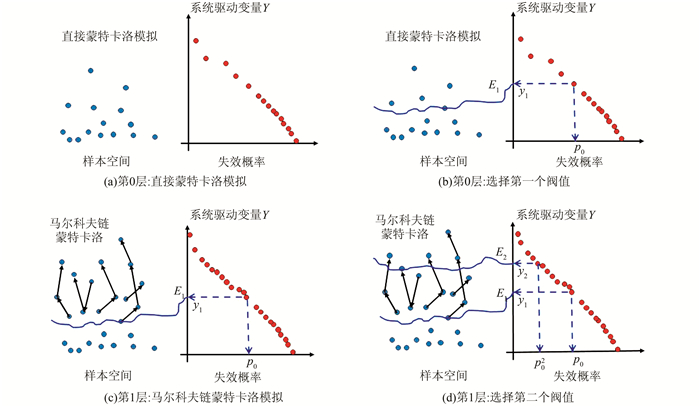
2 基于子集模拟的浅基础扩展可靠度设计方法 2.1 子集模拟子集模拟(SS)[9, 10]是将一个小概率失效事件E表示为一系列具有较高概率的中间失效事件{E1, E2, …, Em},并通过产生中间失效事件的条件样本逐步逼近目标失效区域.本文定义小概率失效事件E的失效区域为E={Y>y},其中Y为子集模拟过程中产生的一系列单调且能反映失效区域信息的系统响应量(即系统驱动变量),y为判断事件E是否发生的阀值.若令y=ym>ym-1>…>y2>y1>0作为m个中间失效事件El={Y>yl, l =1, 2, …, m}的临界阀值,则小概率失效事件E的失效概率P(E={Y>y})可以表达为[7, 9-11]
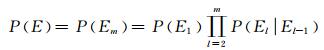 (2)
(2)
式中:P(E1)=P(Y>y1)为事件E1发生的概率;P(El|El-1)={P(Y>yl|Y>yl-1), l=2, …, m}.在计算过程中,y1, y2, …, ym通过对前一个中间失效事件El-1的条件样本的统计分析来确定[7, 9].其所确定的临界阀值yl(l= 1, 2, …, m)使中间失效事件所对应的条件失效概率均等于一个特定的条件概率值p0,在本文中p0取0.1[7, 9-11].
图 1(a)所示子集模拟最开始通过直接MCS模拟产生N个随机样本, 然后计算这N个随机样本对应的驱动变量值Y,并将其按照升序排列,选择第(1-p0)N个Y值作为临界阀值y1(如图 1(b)所示),此时中间失效事件E1=Y>y1的条件失效概率等于p0.接着如图 1(c)所示,利用E1中的p0N个样本通过马尔科夫链蒙特卡洛(MCMC)方法额外产生(1-p0)N个满足中间失效事件E1=Y>y1的条件样本,从而使满足中间失效事件E1=Y>y1的条件样本总数为N.最后如图 1(d)所示,这N个随机样本(满足中间失效事件E1=Y>y1)对应的驱动变量Y被再一次按照升序排列,并选择第(1-p0)N个Y值作为中间失效事件E2的临界阀值y2.此时满足中间失效事件E2=Y>y2的p0N个样本被作为MCMC方法中“种子”, 它另外产生(1-p0)N个满足中间失效事件E2=Y>y2的条件样本,从而使满足中间失效事件E2=Y>y2的条件样本总数仍为N.重复执行这个过程m次,直到满足目标失效事件Em=Y>ym.关于子集模拟的详细算法请参阅相关文献[7, 9-13].
2.2 系统驱动变量Y的定义子集模拟需要定义一个系统驱动变量Y,引导产生的条件样本逐步逼近目标失效区域.定义的Y值通常随着模拟层数的增加而不断地增大,并且应同时反映系统的失效信息.在岩土结构可靠度分析中,Y通常被定义成安全系数FS的倒数[10, 13-15],即Y=1/FS.Y值随着SS模拟层数的增加不断增大,对应的FS则不断减小,这意味着随机模拟中所产生的不确定性参数的样本逐步逼近了失效区域.在浅基础扩展可靠度设计方法中,设计参数B、L和D被视作随机变量.对于一组给定的土体参数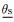
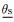
浅基础设计中需要考虑多种失效模式(比如ULS和SLS失效).对于第k种失效模式,其安全系数FSk可表示为
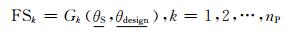 (3)
(3)
式中: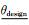
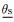
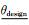
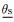
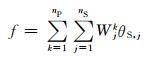 (4)
(4)
式中:Wjk为系统不确定性参数θS, j的敏感系数,反映了FSk对θS, j的敏感度.Wjk可以通过下式进行计算:
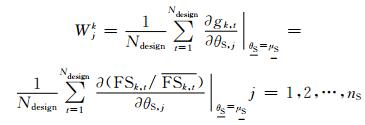 (5)
(5)
式中:Ndesign为设计空间中可能的设计方案数目;FSk, t为设计空间中第t个设计方案的安全系数;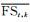
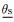
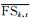
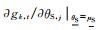
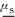
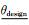
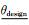
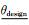
子集模拟完成之后,浅基础设计中涉及的所有不确定性变量(包括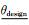
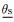
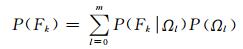 (6)
(6)
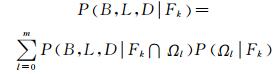 (7)
(7)
式中:P(Fk∣Ωl)表示第k种失效模式在子集Ωl中发生失效的概率,等于Ωl中失效样本数NF, l与总样本数Nl之比;P(Ωl)为子集Ωl的发生概率,当l=0, 1, 2, …, m-1时其值为p0l-p0l+1,当l=m时为p0m;P(B, L, D|Fk∩Ωl)表示在子集Ωl的失效区域(FSk<1的区域)中,第k种失效模式的一个设计方案(B, L, D)发生的概率,即该设计方案在Ωl中的失效样本数与Ωl中的总失效样本数之比;P(Ωl|Fk)表示失效样本落在Ωl中的概率,根据贝叶斯定理计算为P(Fk|Ωl)P(Ωl)/P(Fk).基于子集模拟产生的条件样本,第k种失效模式的失效概率P(Fk)和条件概率P(B, L, D|Fk)可以通过公式(6)~(7)进行估计.将P(Fk)和P(B, L, D|Fk)代入公式(1)中计算得到对应的设计方案的失效概率.
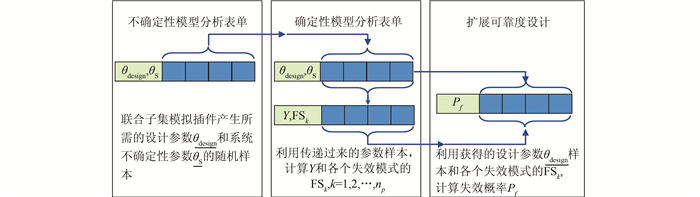
为了便于工程师采用所提出的方法,本文基于EXCEL表单环境,采用Visual Basic Application (VBA)编写了计算程序和用户界面,使整个计算过程清晰明了,简单易行.如图 2所示,所提出方法的不确定性分析模型通过联合子集模拟插件产生所需的设计参数变量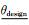
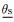
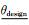
|
| 图 2 所提方法计算原理图 Figure 2 Schematic diagram of proposed method |
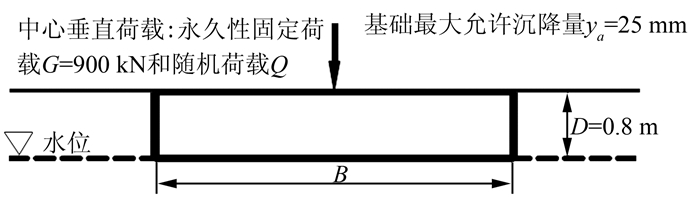
Wang[5]采用如图 3所示的浅基础算例说明和验证了基于直接MCS的扩展可靠度设计方法.如图 3所示,该浅基础受到中心垂直荷载作用.荷载由两部分组成,包括固定荷载G=900 kN和随机活荷载Q.基础埋置于地下水位以上,埋置深度D=0.8 m,土体容重γ=22 kN/m3,土体不确定性参数包括不排水抗剪强度cu、有效内摩擦角φ′ (c′=0)、体积压缩系数mv.基础的埋置深度D为恒定值,其宽度(B)和长度(L)相等.因此该算例关键的设计参数为基础宽度B,其设计值应使基础满足承载能力极限状态(ULS)的设计要求,且最大允许沉降量应小于25 mm(即正常使用极限状态的设计要求).下面将采用本文提出的方法和计算程序对该算例进行重新设计,具体设计过程包括3部分:不确定性分析模型、确定性分析模型、子集模拟和扩展可靠度设计.
4.1 不确定性分析模型不确定性分析模型主要是用来产生各个随机变量对应的随机样本.该浅基础算例中共有4个不确定性变量,分别为随机荷载Q、不排水抗剪强度cu、有效内摩擦角φ′和体积压缩系数mv.这些不确定性参数均符合对数正态分布,它们的均值m和标准差s分别为:mQ = 458.7 kN、sQ = 68.8 kN;m′v=36.4°、s′v=3°;mcu=235.3 kPa、scu=70.6 kPa;mmv=0.018 75 m2/MN、smv=0.007 5 m2/MN,这些统计特征与Wang[5]中采用的值保持一致.此外,在扩展可靠度设计方法中设计参数B为离散型均匀分布的随机变量.在本设计中B的可能取值范围为1~3 m,取值间距为0.1 m.因此,设计空间中共有21个可能的设计方案,与Wang [5]中考虑的设计方案保持一致.
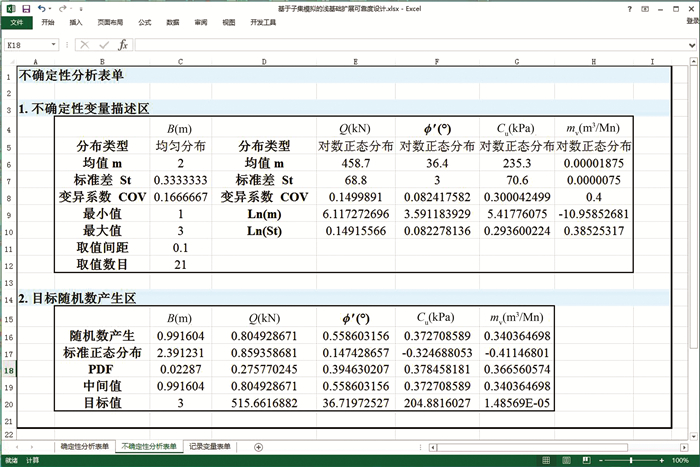
图 4为本文建立的不确定性分析模型.该模型由两部分组成:1)不确定性变量描述区,主要用于描述各个不确定性参数(包括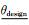
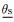
|
| 图 4 不确定性分析模型表单 Figure 4 Uncertainty model worksheet |
确定性分析模型主要用来计算浅基础的安全系数(包括ULS和SLS对应的FSULS和FSSLS)和代理系统响应f.本文采用的FSULS和FSSLS计算方法与Wang[5]一致,详细的计算过程请参阅文献[5].根据公式(4),浅基础算例的代理系统响应f可以通过下式进行计算:
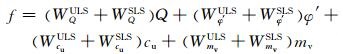 (8)
(8)
式中:WQULS、WQSLS、Wφ′ULS、Wφ′SLS、WcuULS、WcuSLS、WmvULS和WmvSLS分别为不确定性参数Q、φ′、cu、mv在ULS和SLS状态下的敏感系数.根据公式(5),它们的值分别为:-0.000 74、-0.000 74、0.146、0、0、0.001 37、0和-36 098.
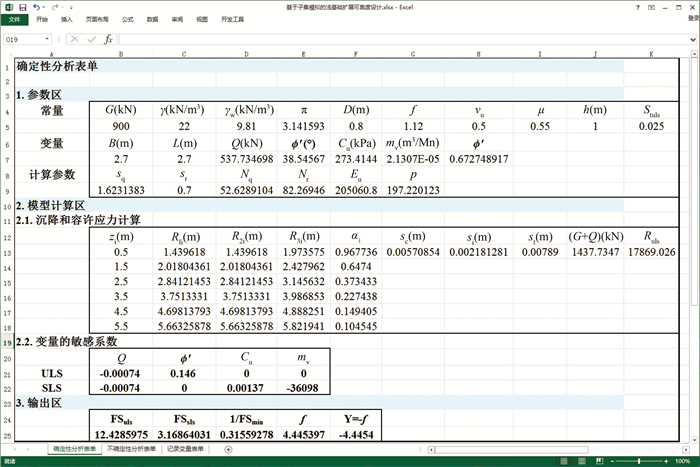
图 5所示为本文建立的确定性分析模型.该模型由3部分组成:第一部分为参数区,主要包括浅基础确定性计算所需的基本参数,其值根据不确定性分析模型传递过来的各个不确定性参数的随机样本计算得到;第二部分为模型计算区,主要是根据参数区的基本参数值计算基础沉降和极限承载力,以及描述了各个土体参数在不同失效模式下的敏感系数;第三部分为输出区,主要包括确定性分析模型计算得到的FSULS、FSSLS、f和1/FSmin(即FSULS和FSSLS中较小值的倒数).当确定性分析模型和不确定性分析模型建立完成之后,将对应的单元格进行连接.然后,调用子集模拟用户界面执行子集模拟,并计算各个设计方案的条件失效概率.
|
| 图 5 确定性分析模型表单 Figure 5 Deterministic model worksheet |
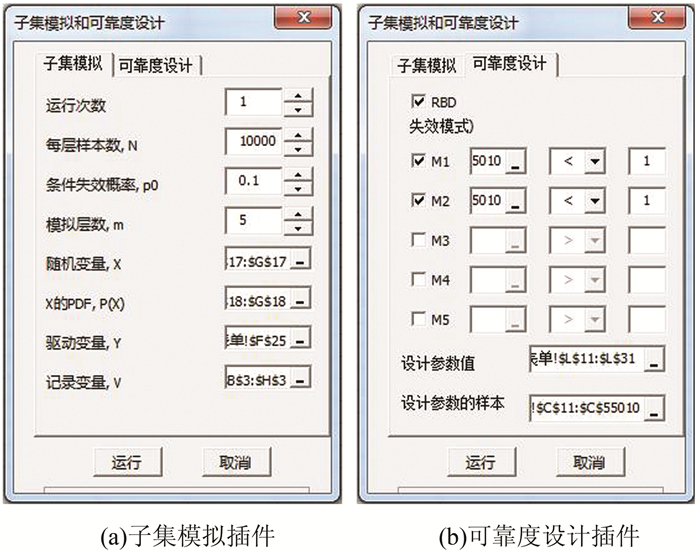
图 6所示为子集模拟和扩展可靠度设计用户界面[7],包括两部分:第一部分(见图 6(a))为子集模拟分析程序,用于执行子集模拟;第二部分(见图 6(b))为扩展可靠度设计程序,根据公式(1)和(6)~(7)以及子集模拟产生的条件样本计算各个设计方案的条件失效概率.如图 6(a)所示,本算例中每层的样本数设置为10 000,条件失效概率为0.1,最高模拟层数为5,驱动变量Y取-f.因此,本算例产生的总样本数为5×(1-0.1)×10 000+10 000=55 000个.子集模拟完成后,该程序会产生一张新的表单记录条件样本.基于这些条件样本,调用如图 6(b)所示的扩展可靠度设计插件,计算各个设计方案的条件失效概率,关于该程序的详细信息可参阅文献[7].
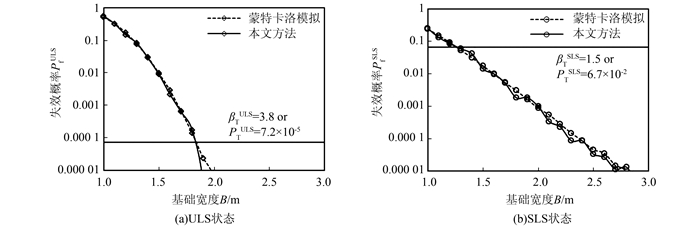
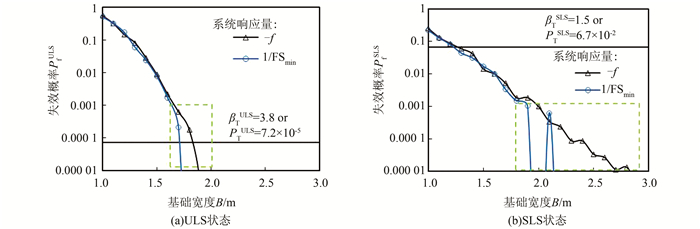
4.4 设计结果图 7(a)和7(b)所示分别为不同设计方案(即不同设计宽度B)在ULS(图 7(a))和SLS状态(图 7(b))下的条件失效概率.其中虚线为Wang[5]采用基于直接MCS的扩展可靠度设计得到的各个设计方案的失效概率,实线为本文方法得到的失效概率.从图中可以看出,两种方法得到的设计结果完全一致.根据ULS和SLS的目标可靠度失效概率pTULS=7.2×10-5和pTSLS=6.7×10-2可以得到ULS的可行设计为B>1.8 m,SLS的可行设计为B≥1.3 m.综上所述,本算例的可行设计由ULS控制,为B>1.8 m,与Wang[5]根据直接MCS得到的可行设计一致.值得注意的是Wang[5]的研究中产生的样本总数为1 000万,而本文方法所使用的样本数只有55 000个.因此,采用本文提出的方法极大地减少了模拟所需要的样本量,显著提高了设计效率.
|
| 图 7 基于子集模拟和直接MCS的条件失效概率 Figure 7 Conditional failure probability from Subset simulation and direct MCS |
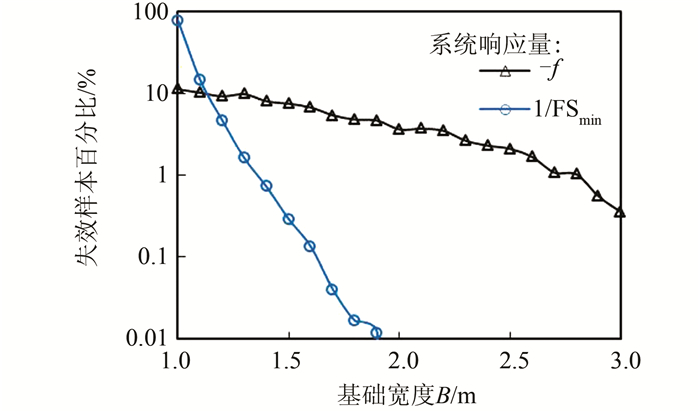
图 8(a)和8(b)所示为子集模拟中采用Y=-f或1/FSmin作为系统驱动变量的条件失效概率.Y=1/FSmin是岩土工程可靠度分析中子集模拟常采用的一种驱动变量形式.从图中可以看出,采用Y=1/FSmin作为子集模拟的驱动变量时,得到的条件失效概率曲线在小概率失效空间(比如图中的虚线矩形框内的区域)的波动性更大,表明采用Y=1/FSmin不能在设计宽度B>1.8 m(即本算例的可行设计区域)的设计空间内产生足够的失效样本.反之,采用Y=-f作为子集模拟的驱动变量解决了这个问题.图 9所示为子集模拟采用不同系统驱动变量在各个设计参数上产生的条件失效样本分布图.当采用Y=1/FSmin作为子集模拟的系统驱动变量时,设计宽度B=1 m对应的失效样本占了总失效样本数的77.9%,失效样本比例随着设计宽度的增加急剧减小,导致在B相对大(如B>1.8 m)的区域缺少失效样本,无法准确地计算B较大设计方案对应的条件失效概率.相反,采用Y=-f作为子集模拟的系统驱动变量,在整个设计区间[1 m, 3 m]内均产生了失效样本,使计算设计空间中所有设计方案的失效概率成为可能.
|
| 图 8 不同系统响应下的条件失效概率 Figure 8 Conditional failure probabilities from SS with different system responses |
|
| 图 9 不同系统响应下,子集模拟获得的失效样本分布 Figure 9 Percentages of failure samples obtained from SS using different system responses |
本文提出了一种基于子集模拟的浅基础扩展可靠度设计方法,构建了一个代理响应辅助子集模拟在扩展可靠度设计中的应用,并以EXCEL表单环境为平台采用Visual Basic Application (VBA)编写了计算程序和用户界面,以便于工程师使用本文所提出的方法.通过一个浅基础算例说明了该方法的准确性和有效性,主要结论如下:
1) 在所提出的代理响应f的辅助下,子集模拟和扩展可靠度方法有效地结合在一起.在扩展可靠度设计中采用f定义子集模拟的驱动变量(即Y=-f)显著改善了失效样本的分布情况,在整个设计空间中产生了所有设计方案的失效样本,提高了小失效概率区域内设计方案的失效概率的计算精度.相对于传统的系统驱动变量Y=1/FSmin,在扩展可靠度设计中采用-f作为驱动变量的优势明显.
2) 通过与采用基于直接MCS的扩展可靠度设计方法得到的设计结果对比,验证了所提出的方法的准确性.相比较直接MCS,所提出的方法显著地减少了设计所需的样本量,极大地提高了扩展可靠度设计方法在小概率设计空间(pT<0.001)的设计效率.
3) 本文编写的扩展可靠度设计程序中确定性分析模型、不确定性分析模型、子集模拟和扩展可靠度设计分别由相对独立的计算模块实现,设计过程清晰明了,简单易行,提高了所提出方法的实用性,有利于本方法在基础工程设计实践中的应用.
| [1] | Building Officials, Code Administrators International. The BOCA National Building Code[S]. Building Officials & Code Administrators International, 1993. |
| [2] | Honjo Y, Kikuchi Y, Suzuki M, et al. JGS comprehensive foundation design code: Geo-Code 21[C]//Proceedings of the International Conference on Soil Mechanics and Geotechnical Engineering. AA Balkema Publishers, 2005, 16(4): 2813. |
| [3] | Frank R. Designers'Guide to EN 1997-1 Eurocode 7: Geotechnical Design-General Rules[S]. Thomas Telford, 2004. |
| [4] |
熊敏, 蒋水华, 李典庆. 中国与欧洲规范关于坝坡抗滑稳定分析方法的比较[J].
武汉大学学报(工学版), 2013, 46(5): 593–598.
Xiong Min, Jiang Shuihua, Li Dianqing. A comparative investigation on slope stability analysis of embankment dams between Chinese and European geotechnical design codes[J]. Engineering Journal of Wuhan University, 2013, 46(5): 593–598. |
| [5] | Wang Y. Reliability-based design of spread foundations by Monte Carlo simulations[J]. Geotechnique, 2011, 61(8): 677–685. DOI:10.1680/geot.10.P.016 |
| [6] |
董前进, 梅亚东, 兰军. 基于Monte Carlo模拟的洪水预报可靠性分析[J].
武汉大学学报(工学版), 2013, 46(5): 545–550.
Dong Qianjin, Mei Yadong, Lan Jun. Reliability analysis of flood forecasting based on Monte Carlo simulation[J]. Engineering Journal of Wuhan University, 2013, 46(5): 545–550. |
| [7] | Wang Y, Cao Z. Expanded reliability-based design of piles in spatially variable soil using efficient Monte Carlo simulations[J]. Soils and Foundations, 2013, 53(6): 820–834. DOI:10.1016/j.sandf.2013.10.002 |
| [8] | Wang Y, AU S K, Kulhawy F H. Expanded reliability-based design approach for drilled shafts[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(2): 140–149. DOI:10.1061/(ASCE)GT.1943-5606.0000421 |
| [9] | AUS K, Beck J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001, 16(4): 263–277. DOI:10.1016/S0266-8920(01)00019-4 |
| [10] | AU S K, Beck J L. Subset simulation and its application to probabilistic seismic performance assessment[J]. Journal of Engineering Mechanics, 2003, 16(4). |
| [11] | AU S K, Cao Z J, Wang Y. Implementing advanced Monte Carlo simulation under spreadsheet environment[J]. Structural Safety, 2010, 32(5): 281–292. DOI:10.1016/j.strusafe.2010.03.004 |
| [12] |
张曼, 唐小松, 李典庆. 含相关非正态变量边坡可靠度分析的子集模拟方法[J].
武汉大学学报(工学版), 2012, 45(1): 41–45.
Zhang Man, Tang Xiaosong, Li Dianqing. Reliability analysis of slope stability involving correlated non-normal variables using subset simulation method[J]. Engineering Journal of Wuhan University, 2012, 45(1): 41–45. |
| [13] |
曹子君, 王宇, 区兆驹. 基于子集模拟的边坡可靠度分析方法研究[J].
地下空间与工程学报, 2013, 2: 425–429.
Cao Zijun, Wang Yu, Au S K. Probabilistic slope stability analysis using subset simulation[J]. Chinese Journal of Underground Space and Engineering, 2013, 2: 425–429. |
| [14] |
曹子君. 子集模拟在边坡可靠性分析中的应用[D]. 成都: 西南交通大学, 2009.
Cao Zijun. Application of subset simulation on reliability analysis of slope stability[D]. Chengdu: Southwest Jiaotong University, 2009. http: //cdmd. cnki. com. cn/Article/CDMD-10613-2010142412. htm |
| [15] | Orr T L L. Design examples for the Eurocode 7 Workshop[C]//Proceedings of International Workshop on Evaluation of Eurocode, 2005, 7, Trinity College, Dublin: 67-74. https: //www. researchgate. net/publication/268378076_Design_Examples_for_the_Eurocode_7_Workshop |
| [16] | Li D Q, Xiao T, Cao Z J, et al. Enhancement of random finite element method in reliability analysis and risk assessment of soil slopes using subset simulation[J]. Landslides, 2015: 1–11. |
 2017, Vol. 50
2017, Vol. 50