文章信息
- 冯蕊, 何蕴龙
- FENG Rui, HE Yunlong
- 超深覆盖层上沥青混凝土心墙堆石坝防渗系统抗震安全性
- Seismic response analysis of seepage control system of asphalt concrete core rockfill dam on thick overburden layer
- 武汉大学学报(工学版), 2016, 49(1): 32-38
- Engineering Journal of Wuhan University, 2016, 49(1): 32-38
- http://dx.doi.org/10.14188/j.1671-8844.2016-01-006
-
文章历史
- 收稿日期: 2015-07-18
在我国水电资源蕴藏丰富的西南地区筑坝,有两个问题需要特别注意,一是河流中深厚覆盖层普遍发育;二是西南地区属强震区.沥青混凝土心墙堆石坝作为一种新坝型,以柔性大、适应变形能力强和抗震性能好等优点[1-5],恰好满足了在高地震烈度区、深厚覆盖层等特殊环境和复杂地质条件下筑坝的要求.我国的沥青混凝土心墙堆石坝绝多数位于强震区[6-10],其中遭遇过地震的只有冶勒坝,由于距震中较远,在汶川地震和雅安庐山地震中大坝强震检测台阵测得的坝顶加速度峰值较小[11],坝体地震反应不强烈,大坝安全运行性态并未受到影响[12].所以对沥青混凝土心墙堆石坝抗震特性的探讨具有重要意义,其中作为土石坝关键环节的防渗系统的抗震安全性更是值得注意.
深厚覆盖层上沥青混凝土心墙堆石坝的防渗系统一般由沥青混凝土心墙、混凝土防渗墙以及连接两者的坝基廊道组成.本文所研究的某座位于大渡河上的沥青混凝土心墙堆石坝,坝址区基本烈度为Ⅷ度,最大坝高85.5 m,河谷覆盖层深56~130 m,覆盖层防渗墙深111.0 m,这种深度大于100 m的坝基防渗墙在我国并不多见,心墙和防渗墙之间采用廊道连接.超深覆盖层的存在对坝体、心墙和廊道的应力变形状况都会有一定的影响.
深厚覆盖层的沉降会加剧心墙拱作用,使心墙与坝壳料之间因弹模差异产生的不均匀沉降增加,同时心墙受到防渗墙的顶托作用,在纵向剪切变形的作用下容易产生裂缝.混凝土防渗墙已经有了较为成熟的发展,成为防渗处理的首选,覆盖层地基中受力条件复杂,墙体有压碎的危险,同时还有可能在墙顶两侧产生拉裂缝.廊道更是整个防渗系统的关键环节,廊道两岸深入基岩内部,在基岩与覆盖层相接部位容易形成应力集中从而产生廊道裂缝,硗碛、瀑布沟大坝中均出现了廊道止水破坏的现象,所以面对防渗系统如此复杂的受力状况,不仅要了解其在静力工况下的运行状态,更要对动力工况时防渗系统的抗震安全性作进一步研究,但是目前对这种复杂情况下防渗系统的受力情况和抗震安全性认识很有限.
本文针对大渡河上某沥青混凝土心墙堆石坝位于强地震烈度区和超深覆盖层上这两个特点,建立了非线性有限元模型,并运用子模型技术对坝体防渗系统进行了精确的模拟,其中各种接触面均采用薄层单元.
1 研究方法 1.1 基于薄层单元的动接触模拟为了实现模型的精确模拟,廊道接缝、防渗墙上下游侧的泥皮以及防渗墙底残渣等各类接触面均采用有厚度的薄层单元[13]以合理模拟基础面的工作形态,在单元刚度矩阵的形成上与普通单元一样,但是在本构矩阵中将法向与切向分开考虑,薄层单元法向应力应变关系借鉴S C Bandis关于岩石节理法向变形的双曲线模型[14].根据正应力判断其接触状态,当接触面张开的时候,具体法向弹模Dnn取小值.
式中:Kni为法向初始受压刚度;σn为单元法向正应力;t 为单元厚度;Vm 为法向最大压缩量.
薄层单元切向应力应变关系采用Clough的剪切双曲线模型[15].当接触面滑移时,具体切向弹模Dns取小值.
式中:Ksi为初始剪切刚度系数;γw为水的容重;τ为单元切向剪应力;τp 为临界剪应力,按摩尔库伦定律计算为τp=c-tanφ·σn;Rf为破坏比.
在动力计算中,阻尼采用Rayleigh阻尼的形式,其阻尼按照附近土体进行近似.
1.2 有限元子模型法子模型方法基于圣维南原理,是指在对整体结构进行计算分析的基础上,在整体模型中切割出一块区域,重新划分网格进行计算分析,这块重新划分网格的细部模型即为子模型,子模型的边界条件采用整体模型相应位置的位移结果.
在土石坝计算分析中,由于材料、受力特性不同,心墙放大脚、心墙混凝土垫座、廊道及其结构缝、廊道与防渗墙的接头、防渗墙及其周围泥皮残渣等都是需要进行精确模拟及计算分析的结构,其静动位移和应力反应都是正确判断防渗结构可靠性的重要依据.但它们和坝体尺寸相差悬殊,不易和坝体一起进行分析,所以子模型方法是对这些细部结构和关键部位进行模拟的很好选择.在整体时程分析的基础上,插值得到子模型边界节点的动位移、速度和加速度等,以此作为动力边界条件加在子模型上.
2 工程实例分析 2.1 工程概况大渡河某水电站位于四川省境内,大坝为沥青混凝土心墙堆石坝,坝顶宽12.0 m、长398.06 m,最大坝高85.5 m.心墙顶部厚0.6 m,向下逐渐加厚到1.1 m,底部有2.0 m高的心墙放大脚,放大脚底最大厚度为2.3 m.坝址区覆盖层深厚,覆盖层防渗墙最大深度111.0 m.心墙与防渗墙之间用廊道连接,廊道为城门洞形,尺寸为3 m×3.5 m.具体结构型式见图 1.
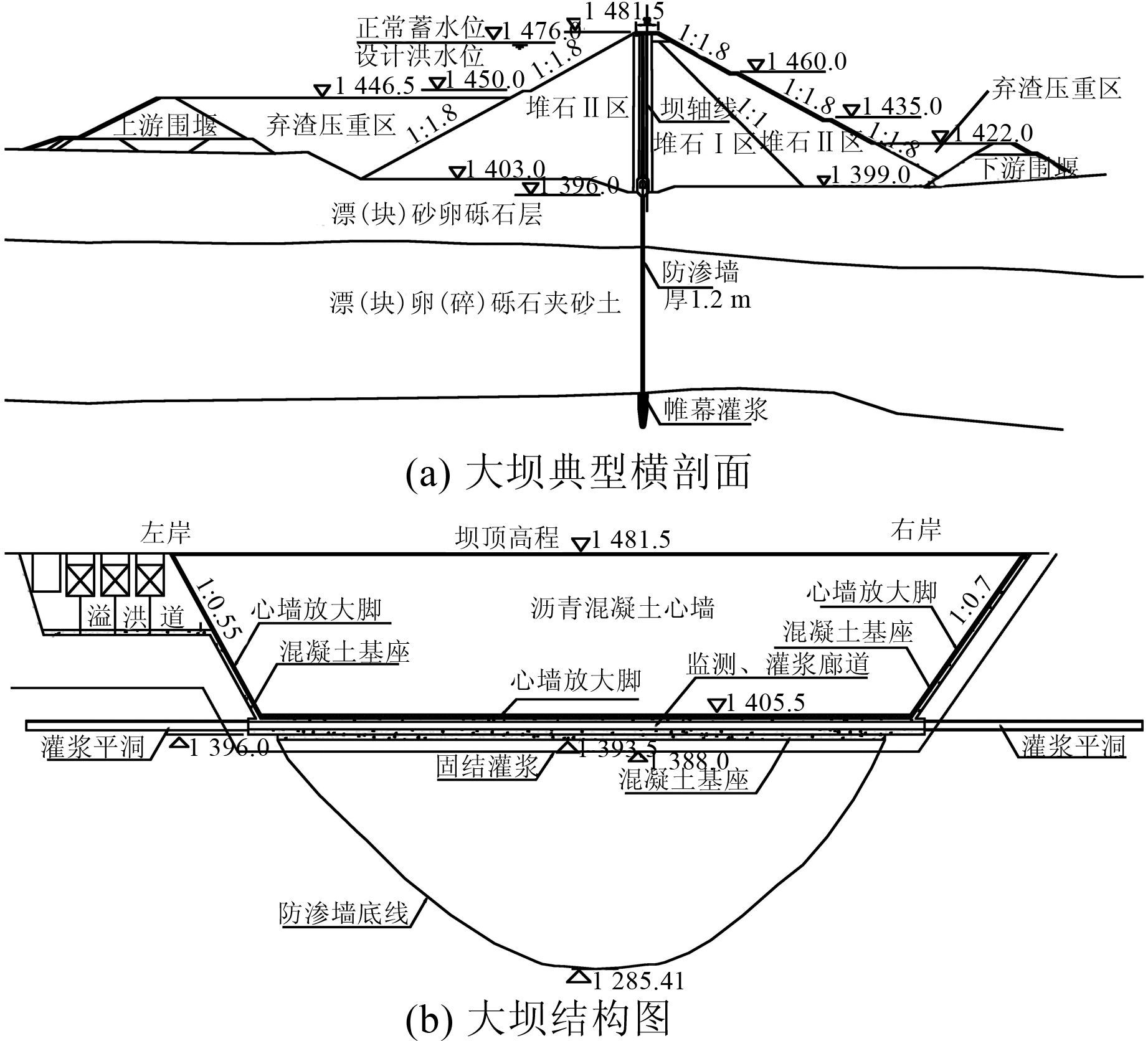
|
| 图 1 大坝结构图 Figure 1 Structural diagrams of the dam |
模型精确模拟了坝体填筑和水库蓄水过程.整体模型有22 436个节点、21 902个单元,子模型有39 075个节点、35 591个单元.模型网格见图 2.
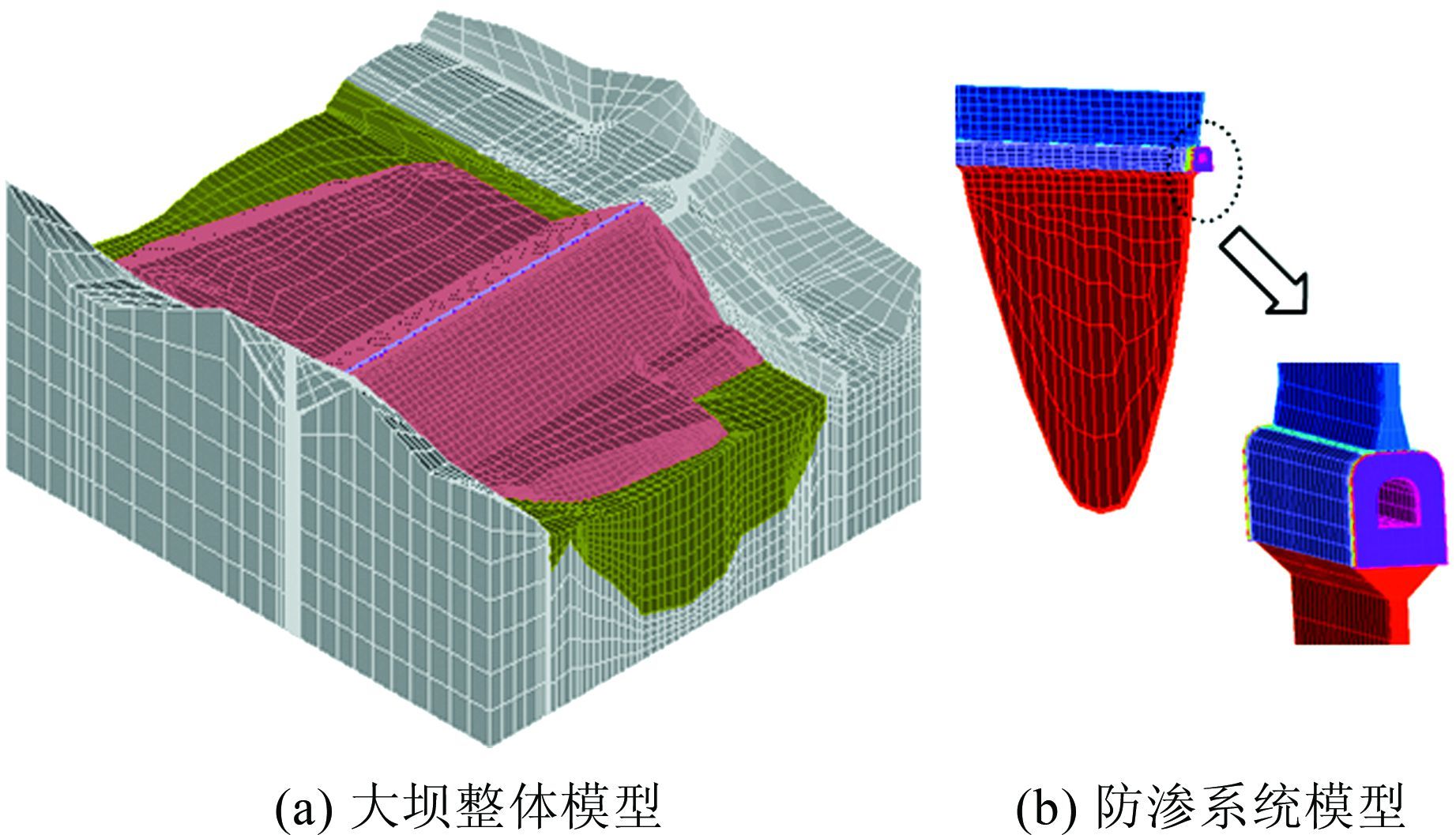
|
| 图 2 有限元模型图 Figure 2 FEM mesh model |
堆石、沥青混凝土、覆盖层的静力计算模型采用 Duncan E~μ非线性弹性模型,动力计算采用Har-din等效黏弹性模型,具体材料参数为试验所得,见表 1和表 2.接触面单元参数见表 3.混凝土廊道、垫座、防渗墙和基岩均采用线弹性模型,混凝土弹模30 GPa,泊松比0.176,密度2 400 kg/m3,基岩弹模8 GPa,泊松比0.25,动力计算时弹模在此基础上提高30%.为了消除坝基岩体对地震动的放大作用,采用无质量基岩进行计算.
| 材料类型 | ρd/(t·m-3) | k | n | G | F | D | Rf | C/kPa | ø0/(°) | Δø/(°) |
| 心墙料 | 2.50 | 640 | 0.15 | 0.47 | 0 | 0 | 0.83 | 370 | 35.0 | 5.0 |
| 过渡1 | 2.24 | 1 149 | 0.37 | 0.29 | 0.100 | 8.1 | 0.72 | 194 | 50.5 | 7.1 |
| 过渡2 | 2.27 | 1 207 | 0.39 | 0.29 | 0.097 | 8.6 | 0.72 | 214 | 51.5 | 7.6 |
| 堆石Ⅰ | 2.06 | 997 | 0.29 | 0.29 | 0.116 | 4.9 | 0.81 | 103 | 45.8 | 4.6 |
| 堆石Ⅱ | 2.11 | 805 | 0.23 | 0.23 | 0.090 | 4.8 | 0.76 | 157 | 49.1 | 6.5 |
| 覆盖层1 | 2.23 | 1 100 | 0.23 | 0.38 | 0.163 | 5.7 | 0.81 | 10 | 47.0 | 5.7 |
| 覆盖层2 | 2.21 | 1 200 | 0.25 | 0.35 | 0.160 | 5.0 | 0.80 | 10 | 47.1 | 5.6 |
| 材料类型 | Kmax | n | λmax | γr |
| 心墙料 | 2 000 | 0.200 | 0.28 | 0.000 8 |
| 过渡1 | 1 050 | 0.613 | 0.24 | 0.000 4 |
| 过渡2 | 2 920 | 0.452 | 0.24 | 0.000 1 |
| 堆石料 | 3 100 | 0.468 | 0.24 | 0.000 1 |
| 覆盖层 | 2 260 | 0.504 | 0.10 | 0.000 1 |
| 项目 | φ/(°) | c/kPa | Rf | Ksi | n | Kni/(MPa·m-1) |
| 泥皮 | 11 | 10.5 | 0.89 | 757 | 0.8 | 300 |
| 残渣单元 | 41 | 0 | 0.84 | 2 500 | 0.76 | 400 |
根据中国地震局地质研究所的报告,坝址区基本烈度为Ⅷ度,地震动峰值加速度为220 g.利用设计地震反应谱为目标谱生成的地震加速度时程曲线进行分析.通过SHAKE91程序反演后,坝基水平向基岩地震波峰值为174 g,具体见图 3.
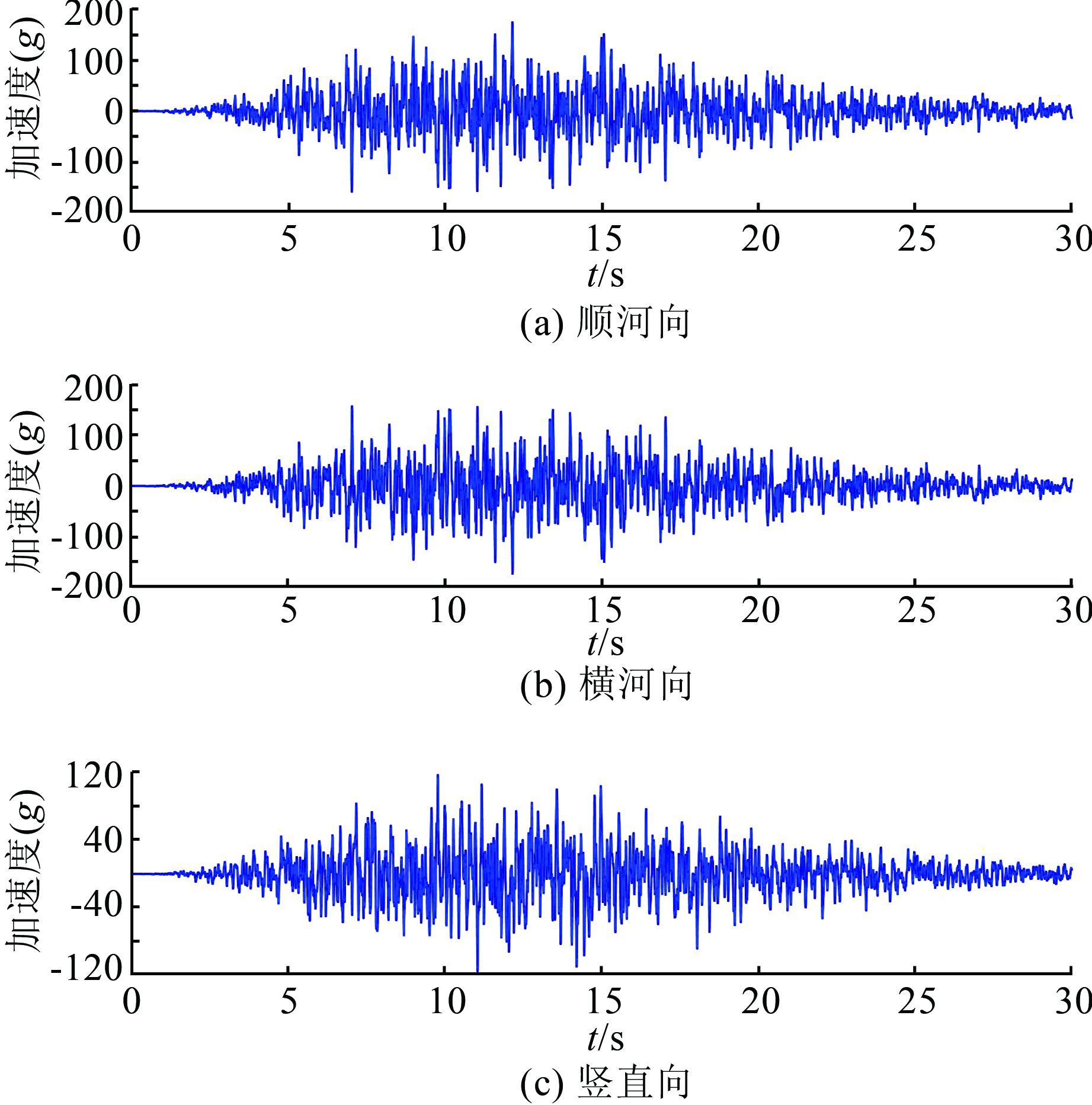
|
| 图 3 基岩地震加速度时程曲线 Figure 3 Bedrock’s earthquake acceleration curve |
心墙顺河向、横河向、竖直向绝对加速度最大值分别为 6.08、4.62、3.98 cm/s2,相应的放大倍数为2.76、2.10、2.71,动位移最大值分别为8.32、4.79、2.21 cm.由于心墙两岸和底部的约束作用较强,3向加速度和动位移的反应最大值均出现在墙顶中央并呈现向底部和两岸逐渐减小的趋势,图 4列出了心墙顺河向最大加速度分布.
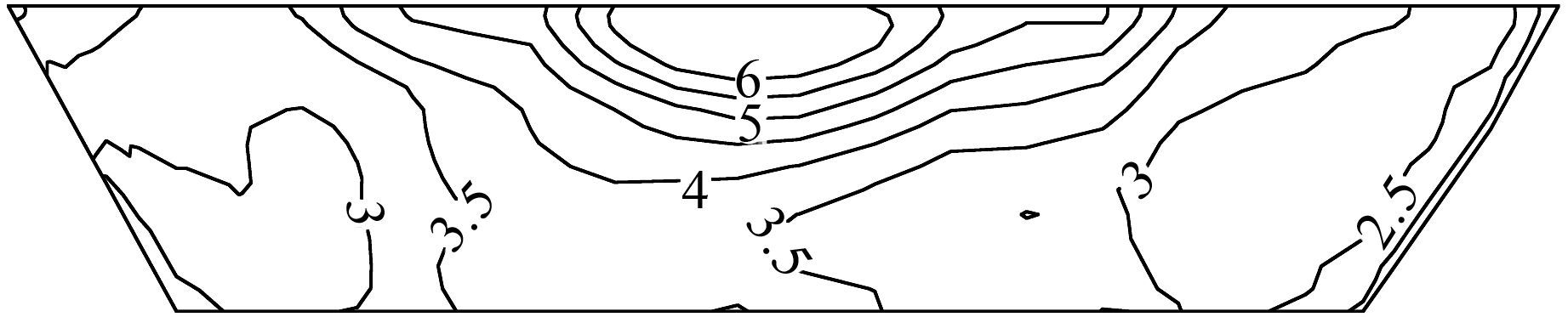
|
| 图 4 沥青混凝土心墙顺河向绝对加速度反应极值(单位:cm/s2) Figure 4 Acceleration maximum reflection of asphalt concrete core in up-downstream direction (unit:cm/s2) |
心墙顺河向静位移随高程变化,在下部1/4墙高处有最大值30.78 cm,向底部和顶部逐渐减小;动位移最大值的分布规律为在墙顶中央达到最大值8.32 cm,向底部和两岸逐渐减小;静动荷载的共同作用后,位移分布规律与静力工况相同,极值仍出现在下部1/4墙高处(达34.88 cm),由于动位移与静位移分布规律的不一致,动静叠加后心墙的挠跨比反而减小,由0.1%变为0.05%.
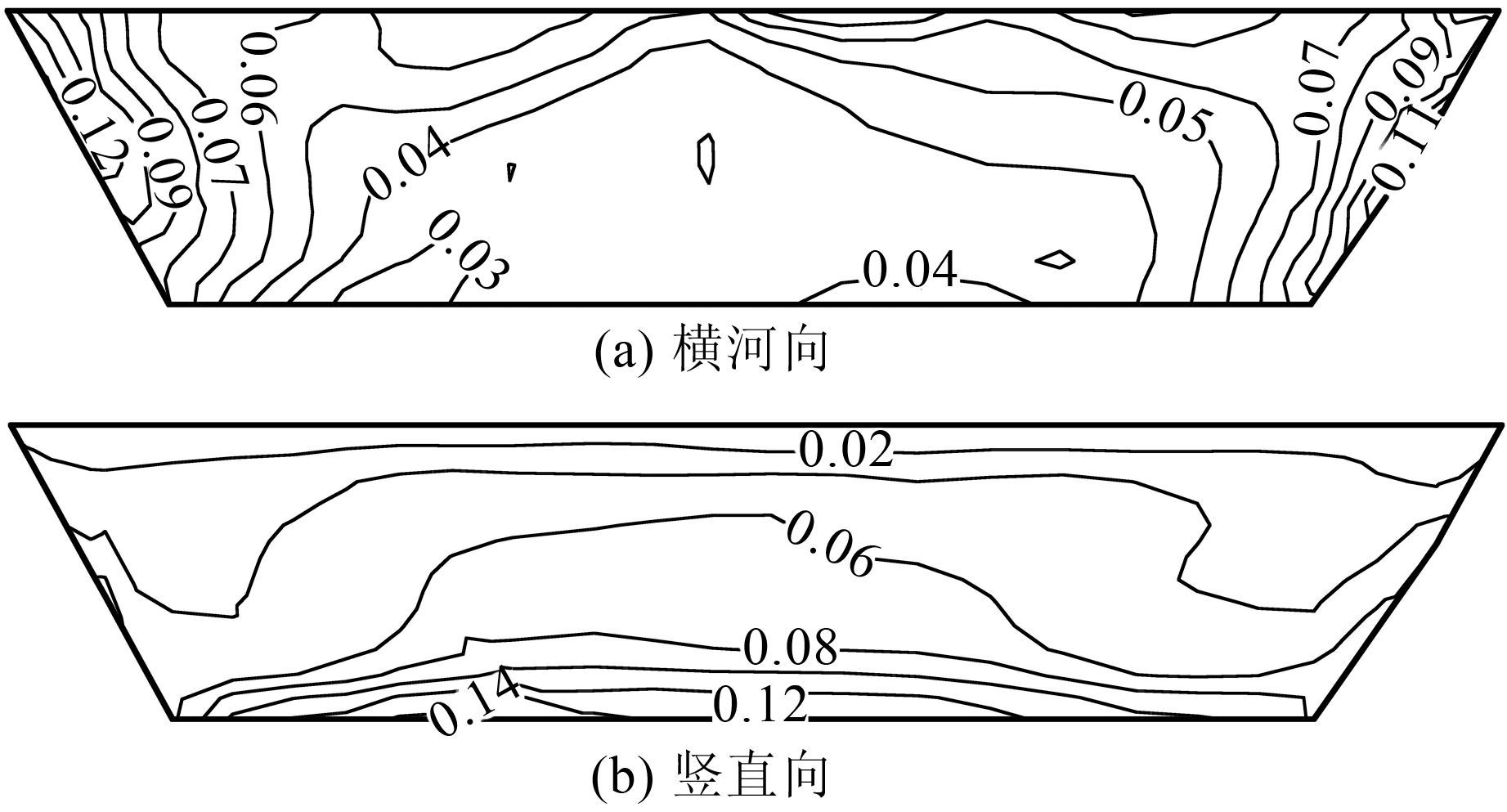
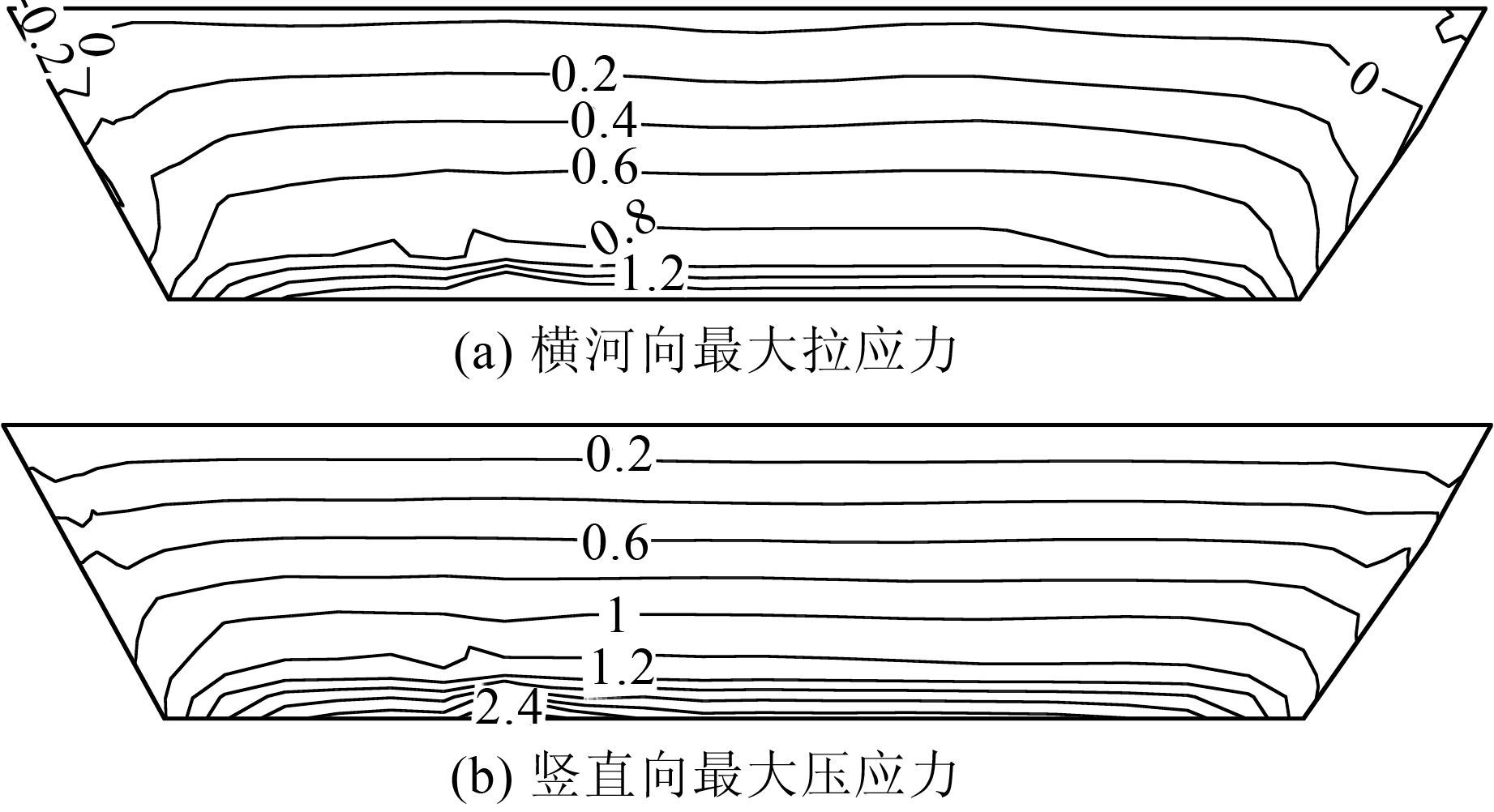
心墙横河向动应力反应最大值为0.13 MPa,出现在约束作用较强的左右岸侧.竖向动应力反应最大值为0.16 MPa,出现在约束较大的墙体底部与廊道接触处,图 5为心墙中央纵剖面最大动应力反应.横河向在静力作用下除了两岸墙顶出现小范围拉应力外,均处于受压状态,静动荷载共同作用下心墙的拉应力分布区遍布整个心墙顶部,仍是在两岸墙顶达到最大.图 6为静动荷载共同作用的情况,图 6(a)为横河向拉应力最不利情况时的心墙应力最大值,最大拉应力由-0.17 MPa增至-0.26 MPa,增幅为52.9%.静动荷载共同作用下竖直向整个心墙仍全部处于受压状态,随着高程的减小,压应力逐渐增大,图 6(b)为竖直向压应力最不利情况时的心墙应力最大值,最大压应力由2.38 MPa增至2.51 MPa,增幅为5.5%.
|
| 图 5 沥青混凝土心墙最大动应力(单位:MPa) Figure 5 Dynamic stress maximum reflection of asphalt concrete core (unit:MPa) |
|
| 图 6 沥青混凝土心墙动静叠加后应力(单位:MPa) Figure 6 Stress contour maps of asphalt concrete core after (unit:MPa) |
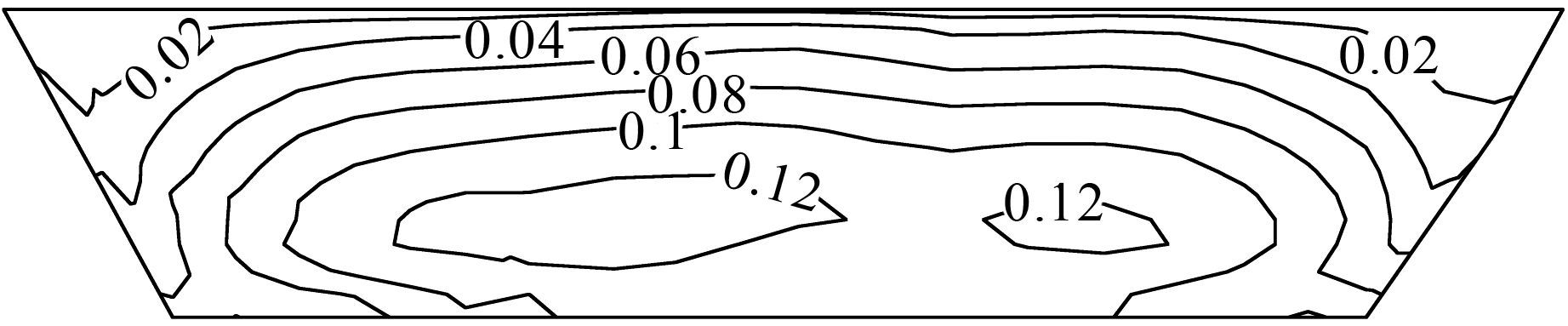
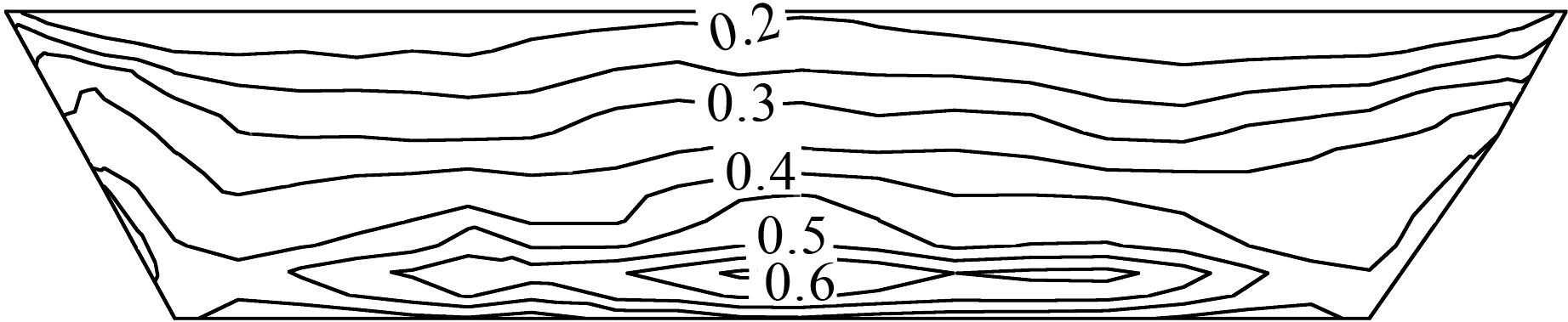
图 7为心墙最大动剪应力,最大有0.13 MPa,数值较小.图 8为沥青混凝土心墙剪应力水平的极值分布情况,和地震之前相比有32.6%的增幅,但是剪应力水平仍较小,无单元破坏情况.
|
| 图 7 沥青混凝土心墙最大动剪应力(单位:MPa) Figure 7 Dynamic shear stress maximum reflection of asphalt concrete core (unit:MPa) |
|
| 图 8 沥青混凝土心墙的剪应力水平 Figure 8 Shear stress’s ratio of asphalt concrete core |
廊道处于坝体内部,受约束较大,加速度和动位移整体较小.顺河向、横河向、竖直向绝对加速度最大值分别为 3.78、2.76、2.46 cm/s2,动位移最大值分别为2.05、0.63、0.60 cm.图 9为廊道顶部沿坝轴线方向的加速度和动位移分布,顺河向中部数值明显较大,由于两端深入基岩所受约束较强,向两端逐渐减小.横河向、竖直向反应较小,且在整个廊道内分布均匀.各桩号位置相差不大.
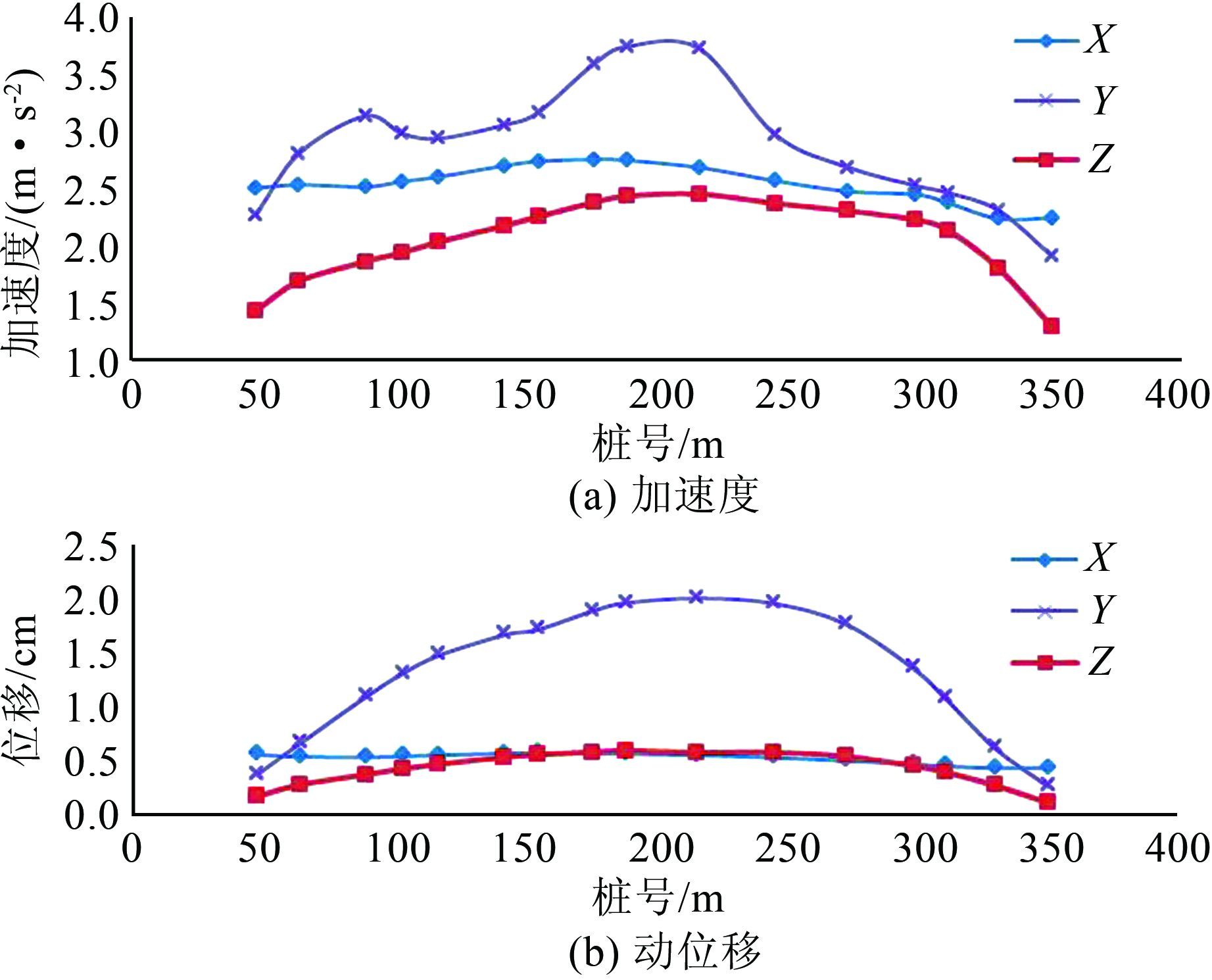
|
| 图 9 廊道最大绝对加速度和最大动位移分布 Figure 9 Maximum accelerations and displacements along the top of the gallery |
由于覆盖层与混凝土、基岩的材料性质存在较大差异,静力计算时在廊道与防渗墙和基岩接触区域出现了应力集中,且为整个廊道的应力极值所在区域,具体表现为上游面受拉、下游面受压.在动力计算中此区域正是廊道3个方向动力反应最强烈的区域,其中横河向动应力最大,分布在廊道右岸下游侧底部与防渗墙接触处,达到1.11 MPa.图 10为静动荷载共同作用时的廊道受力,图 10(a) 为横河向拉应力最不利时的上游面应力最大值,只是数值上的增加,拉应力区域并没有明显增大.图 10(b) 为横河向压应力最不利时的下游面应力最大值,极值由26.20 MPa增大到27.16 MPa.
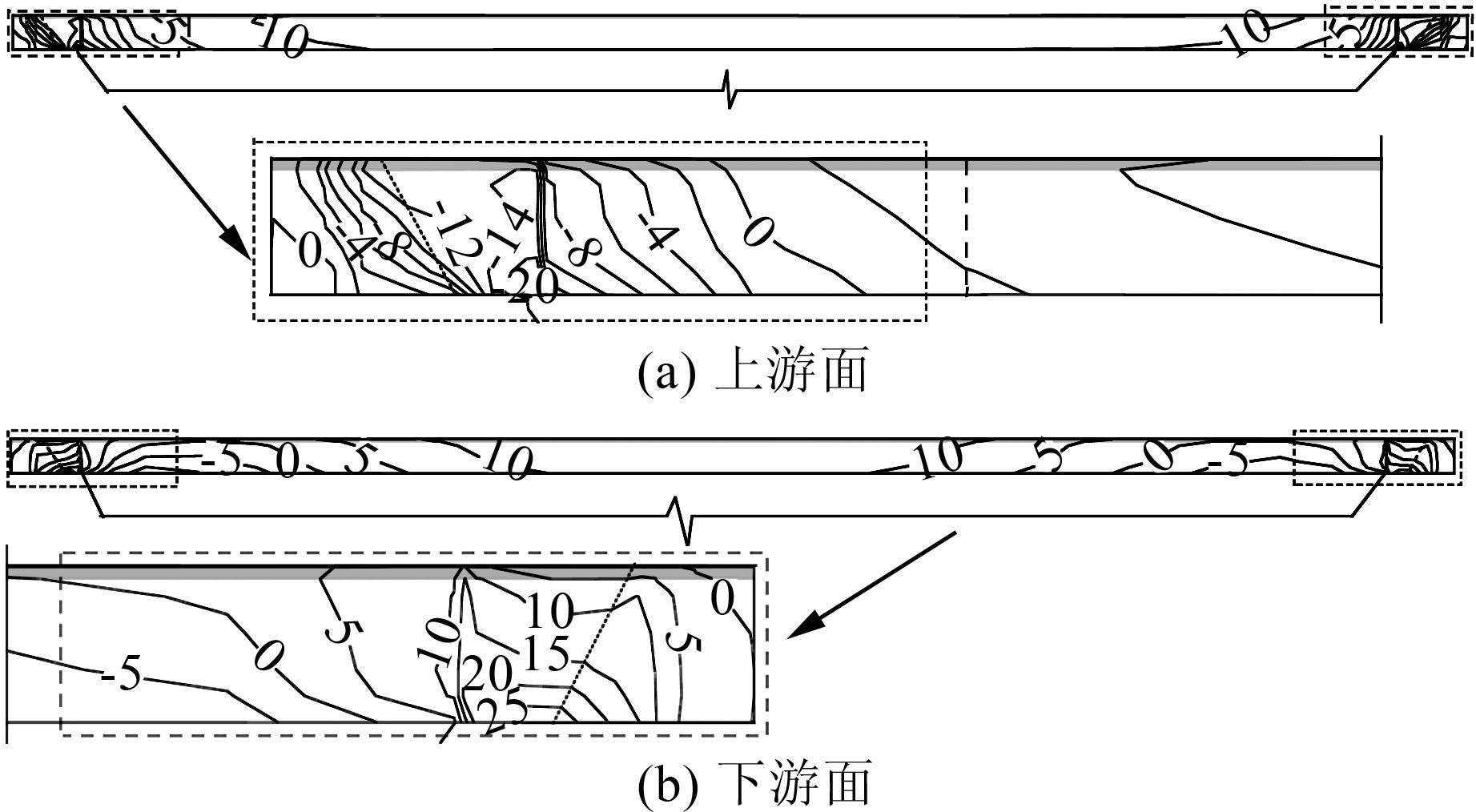
|
| 图 10 静动荷载共同作用下廊道应力(单位:MPa) Figure 10 Stress contour maps of the gallery after superposing the dynamic response with static response (unit:MPa) |
除极值区域外,整个廊道在静力计算时河床坝段上、下游面均出现较大压应力;左右岸1/4跨靠近两岸侧区域,廊道下游面为拉应力较大区域,上游面为压应力较大区域;动力计算时,廊道的动应力在整个廊道内分布比较均匀.静动荷载共同作用下,河床段的压应力由13.93 MPa增大到14.60 MPa,增幅为4.85%.下游1/4跨的拉应力区域几乎没有变化.
由于覆盖层的存在,廊道两岸与基岩接触处发生不均匀沉降,同时加上横向水荷载的作用,廊道与两岸平洞之间产生了较复杂的3向相对变形.表 4列出了地震荷载作用下廊道与两岸平洞接缝的相对变形情况,可以看到法向变形最大,廊道与两岸平洞有张开的趋势,左岸为1.5 mm,右岸为1.7 mm.和静力变形值22 mm(左岸)、20 mm(右岸)相比数值较小.
| 项目 | 法向变形/ mm | 顺河向最大错动/mm | 最大沉降差/mm | |
| 张开 | 压缩 | |||
| 左岸接缝 | 1.5 | 1.8 | 0.7 | 0.5 |
| 右岸接缝 | 1.7 | 2.0 | 0.7 | 0.4 |
防渗墙位于覆盖层内部,受周围约束较大,整体加速度和动位移反应较小,在墙顶中央反应最为强烈,向底部和两岸逐渐减小,同静位移分布规律一致.顺河向、横河向、竖直向绝对加速度最大值分别为3.43、2.71、2.25 cm/s2,横河向和竖直向在整个防渗墙内分布较均匀,各部位加速度值相差不大,图 11为防渗墙最大加速度分布.顺河向动位移最大为1.8 cm,相对于静位移34.7 cm来说,反应较小.横河向和竖直向动位移分别为0.59、0.57 cm.
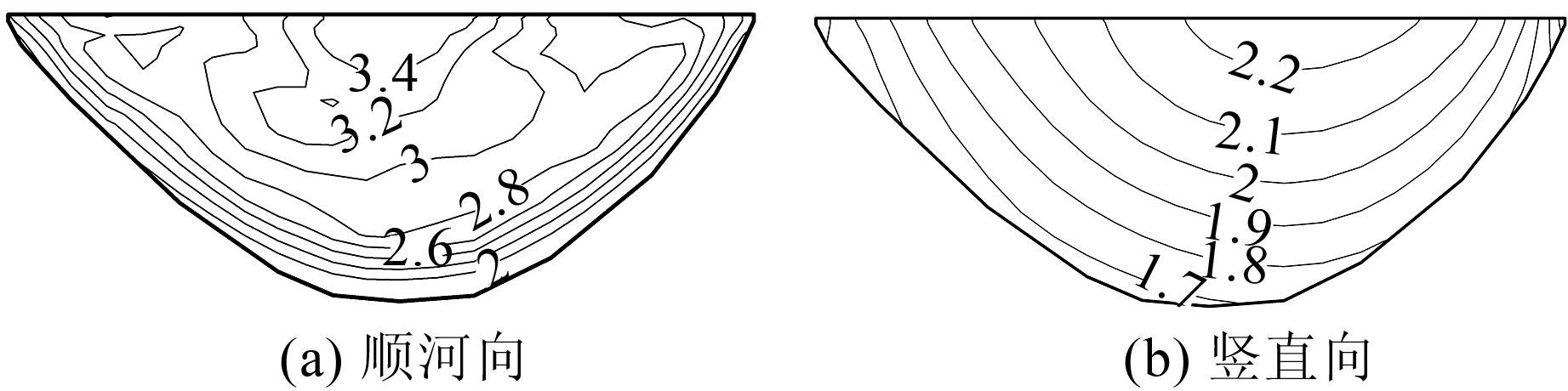
|
| 图 11 防渗墙绝对加速度极值反应 (单位:m/s2) Figure 11 Acceleration maximum reflection of cutoff wall (unit:m/s2) |
图 12为防渗墙最大动应力分布.总体来讲,防渗墙竖直向动应力大于横河向.由于墙顶两岸横向约束作用较大,横河向最大动应力反应在墙顶两端最强烈,向河床中部和下部逐渐变小,最大值为0.69 MPa.竖直向动应力则在最大墙高的河床部位反应最强烈,向左右岸和底部逐渐减小,最大值为1.08 MPa.
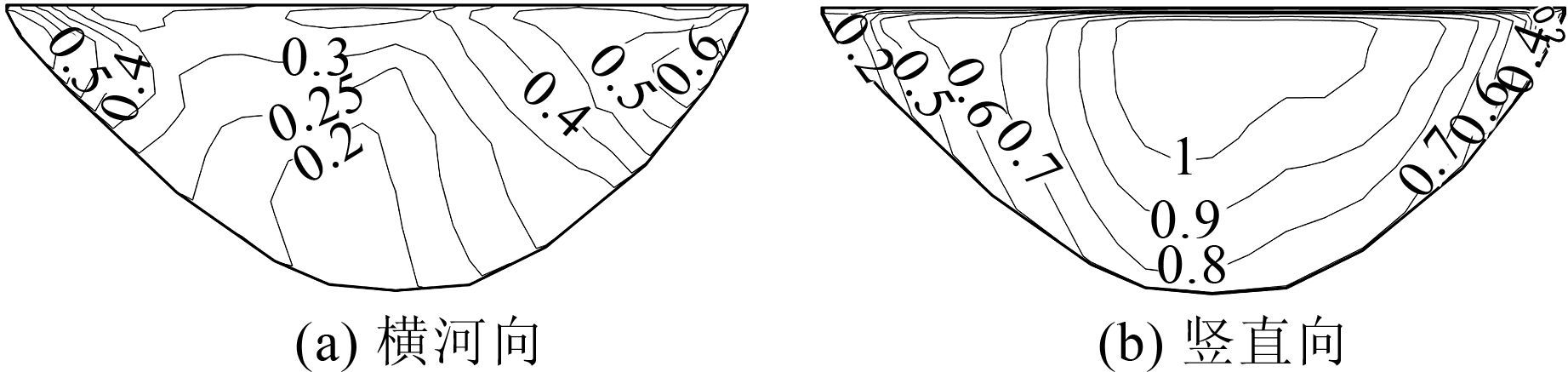
|
| 图 12 防渗墙最大动应力包络值 (单位:MPa) Figure 12 Maximum dynamic stresses of the cutoff wall (unit:MPa) |
静力荷载作用时,防渗墙总体受压,横河向压应力极值出现在墙顶中央,竖直向压应力极值出现在1/3墙高处的中央部位.防渗墙仅在两岸墙顶部位存在横河向和竖直向拉应力.以下仅分析数值较大的横河向拉应力和竖直向压应力.
图 13为静动荷载共同作用下防渗墙的受力情况.首先分析墙顶两岸部位,对横河向应力而言,地震作用下墙顶两端区域动力反应强烈,在静力计算中此处又为拉应力极值区.静动荷载共同作用时,此处拉裂的危险会增加,图 13(a)为横河向拉应力最不利情况时的防渗墙应力最大值,横河向拉应力由静力工况时的-2.32 MPa 增加到-2.94 MPa,增幅为 26.7%,并且出现拉应力范围在左、右岸向河床位置分布增加了4和3.5 m,图 13(c)为拉应力区域变化图,图 13(d)中则标出了超过混凝土抗拉强度的区域.
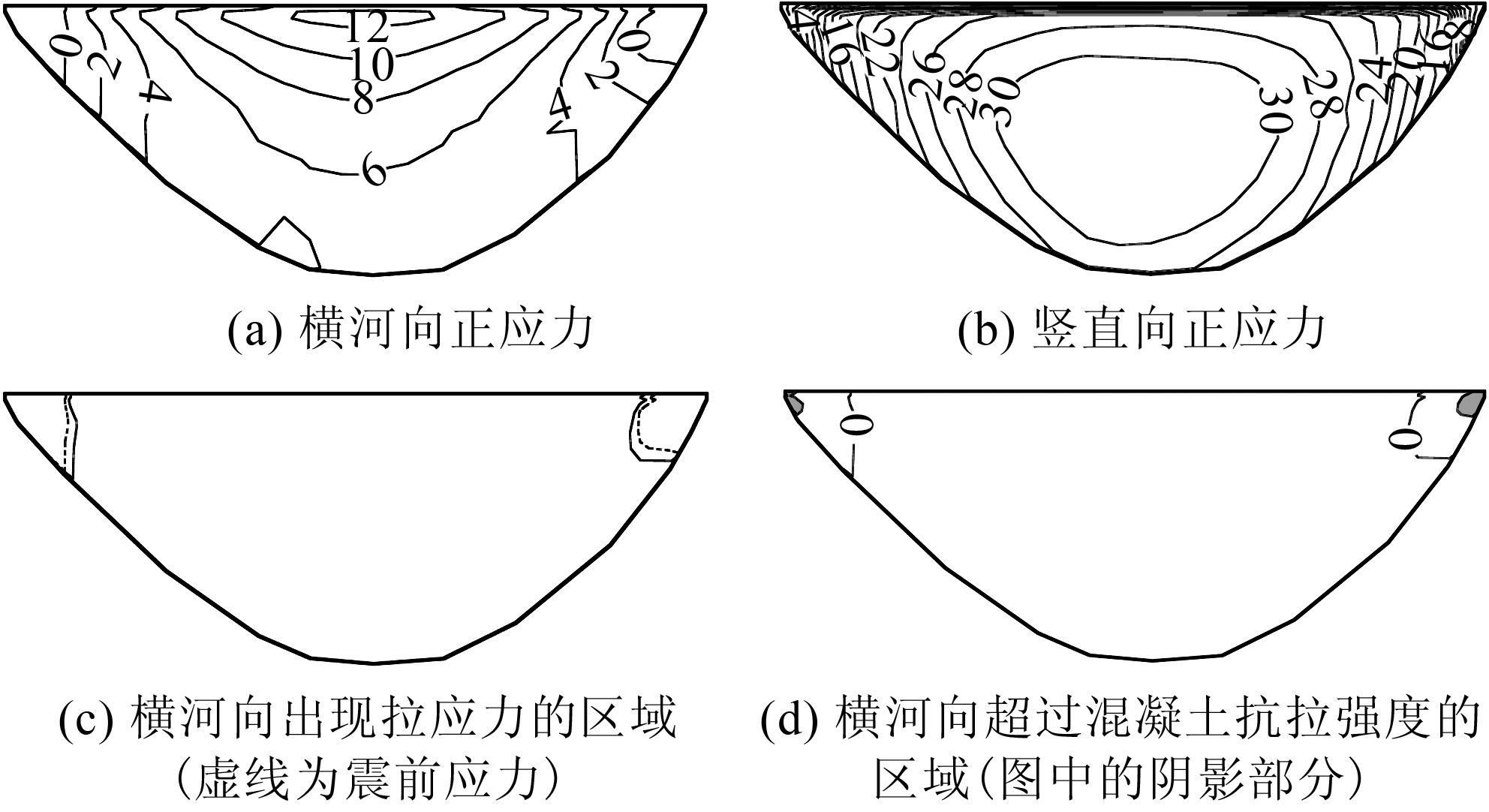
|
| 图 13 静动荷载共同作用下防渗墙应力(单位:MPa) Figure 13 Stress contour maps of the cutoff wall after superposing the dynamic response with static response (unit:MPa) |
对河床部位进行分析:对竖直向应力而言,地震作用下防渗墙中上部动应力反应最强烈,在静力计算时此区域又为竖直向压应力极值区.静动荷载共同作用时,会对河床部位产生不利影响,图 13(b)为静动荷载共同作用时竖直向压应力最不利情况的防渗墙应力最大值.压应力由原来的31.68 MPa 增长为32.57 MPa,由于静力基值较大,增加的比例并不是很大,只有2.8%.
2.4 讨论地震作用下,心墙剪应力水平仍然小于1,没有破坏单元出现,但是剪应力水平相对于静力工况有了32.6% 的增幅,可以看出地震作用在心墙中产生了比较强的剪切作用;心墙顶部两岸区域震前为拉应力极值区,地震时横河向动力反应较强烈,静动荷载共同作用下,此处防渗墙被拉裂的危险增加.
廊道两岸与防渗墙和基岩接触处在静力计算时出现较明显的应力集中,为坝体应力极值区.地震过程中此处又为廊道动力反应最强烈的区域,其余区域动力反应比较均匀.静动荷载共同作用后,下游面的压应力极值由26.20 MPa增大到27.16 MPa.由于震前应力基值较大,增幅并不是很大.地震引起的廊道与两岸平洞接缝的位错变形左岸为1.5 mm、右岸为1.7 mm,和静力变形值22 mm(左岸)、20 mm(右岸)相比数值较小.说明Ⅷ度地震对接缝性态的影响不大.
防渗墙顶靠近两岸的区域由于受到较强的横河向约束作用,静力计算时出现横河向拉应力极值,动力计算时此处又是横河向动力反应最强烈的区域,静动荷载共同作用时,拉应力的区域范围在左、右岸分布向河床增加了4和3.5 m,但是由于混凝土静态抗拉强度比动态抗拉强度小,所以超过抗拉强度的区域几乎不变.竖直向静动力反应均比较强烈的河床中上部区域压应力由原来的31.68 MPa 增长为32.57 MPa,由于静力基值较大,增加的比例并不是很大,为2.8%.说明Ⅷ度的地震对防渗墙的抗压安全性影响不大,但是地震荷载导致的两岸墙顶拉应力区域的增大在廊道配筋计算时仍然值得注意.
3 结论本文以大渡河上的某碾压沥青混凝土心墙堆石坝为工程背景,研究了位于深厚覆盖层上的沥青混凝土心墙堆石坝的防渗系统在Ⅷ度地震时的动力反应规律,初步结论如下:
1) 沥青混凝土心墙的绝对加速度和动位移最大反应值均从墙顶中央向两岸和底部逐渐减小.顺河向反应最大,动位移为8.32 cm,为静位移的27%.由于静、动位移的变形规律并不一致,所以静动荷载共同作用后心墙的挠跨比反而有了很大程度的减小.
2) 心墙横河向动应力反应在横向约束作用较强的心墙左右岸侧最大.心墙竖直向动应力反应在竖向约束作用较强的心墙底部最大.横河向拉应力区震前只出现在两岸墙顶,在静动荷载共同作用下遍布整个心墙顶部,最大值增幅达52.9%.竖直向仍处于全墙受压状态,心墙底部的压应力极值增幅达5.5%.心墙剪应力值较小,剪应力水平与地震之前相比有32.6%的增幅,但并不会对心墙造成破坏.
3) 廊道受周围坝体和基岩约束,加速度和动位移反应整体较小.顺河向最大,在廊道中央反应强烈.横河向和竖直向在整个廊道的反应则比较均匀.
4) 地震作用下廊道与两岸平洞之间发生了较复杂的3向相对变形,但是相对于震前的变形很小,并不会对接缝的安全性态造成影响.
5) 廊道3个方向的上下游动应力反应均在和防渗墙接触部位最为强烈处,其余位置动应力分布比较均匀.此处在静力计算时产生明显的应力集中.上游侧拉应力区域几乎没有变化,仅有数值上的小幅增加,下游侧压应力极值由26.20 MPa增大到27.16 MPa.地震作用下应力集中区应力增幅很小,应力集中并没有产生明显恶化.
6) 防渗墙横河向和竖直向动力反应最强烈的区域分别是横河向约束作用较大的墙顶两岸和具有最大坝高的河床部位中上部.同时这两个区域又为静力计算时横河向拉应力和竖直向压应力极值区.静动荷载共同作用下,防渗墙拉、压应力极值均有小幅增加,防渗墙顶部拉应力区向河床部位有明显的发展,在防渗墙配筋时需要注意.综合看来对防渗墙工作形态影响不大.
| [1] |
王为标, 张应波, 朱悦, 等. 沥青混凝土心墙石渣坝的有限元计算分析[J].
水力发电学报, 2010, 29(4): 173–178.
Wang Weibiao, Zhang Yingbo, Zhu Yue, et al. Finite element analysis of asphalt concrete core rock-debris dam[J]. Journal of Hydroelectric Engineering, 2010, 29(4): 173–178. |
| [2] |
王为标, 申继红. 中国土石坝沥青混凝土心墙简述[J].
石油沥青, 2002(4): 27–31.
Wang Weibiao, Shen Jihong. Asphalt concrete cores for embankment dams in China[J]. Petroleum Asphalt, 2002(4): 27–31. |
| [3] |
王为标. 土石坝沥青防渗技术的应用和发展[J].
水力发电学报, 2004, 23(6): 70–74.
Wang Weibiao. Development and applications of impervious asphalt concrete for embankment dams[J]. Journal of Hydroelectric Engineering, 2004, 23(6): 70–74. |
| [4] |
李志强, 张鸿儒, 侯永峰, 等. 土石坝沥青混凝土心墙三轴力学特性研究[J].
岩石力学与工程学报, 2006, 25(5): 997–1002.
Li Zhiqiang, Zhang Hongru, Hou Yongfeng, et al. Triaxial test study on mechanical characteristics of asphalt concrete in the core wall of earth-rock fill dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(5): 997–1002. |
| [5] |
郝巨涛. 国内沥青混凝土防渗技术发展中的重要问题[J].
水利学报, 2008, 39(10): 1213–1219.
Hao Jutao. Important topics in development of asphalt concrete technology in China[J]. Journal of Hydraulic Engineering, 2008, 39(10): 1213–1219. |
| [6] |
朱晟. 沥青混凝土心墙堆石坝三维地震反应分析[J].
岩土力学, 2008, 29(11): 2933–2938.
Zhu Cheng. 3-D seismic response analysis of rockfill dam with asphalt concrete core[J]. Rock and Soil Mechanics, 2008, 29(11): 2933–2938. |
| [7] |
朱晟, 曹广晶, 张超然. 茅坪溪土石坝安全复核[J].
水利学报, 2014(11): 124–128.
Zhu Sheng, Cao Guangjing, Zhang Chaoran. Verification of rockfill dam safety according to back analysis of Monitoring data[J]. Journal of Hydraulic Engineering, 2014(11): 124–128. |
| [8] |
张红艳, 白长青, 王文进, 等. 三种本构沥青混凝土心墙土 石坝特性[J].
应用力学学报, 2010, 27(4): 709–715.
Zhang Hongyan, Bai Changqing, Wang Wenjin. A comparison of three different models to predict the stress and deformation characteristics of earth-rockfill dam with asphalt concrete core-wall[J]. Chinese Journal of Applied Mechanics, 2010, 27(4): 709–715. |
| [9] |
胡春林, 胡安明, 李友华. 茅坪溪土石坝沥青混凝土心墙的力学特性与施工控制[J].
岩石力学与工程学报, 2001, 20(9): 742–746.
Hu Chunlin, Hu Anming, Li Youhua. Mechanics property and construction of the asphaltic concrete core wall in embankment dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(9): 742–746. |
| [10] |
汪明元, 周欣华, 包承纲, 等. 三峡茅坪溪高沥青混凝土心墙堆石坝运行性状研究[J].
岩石力学与工程学报, 2007, 26(7): 1470–1477.
Wang Mingyuan, Zhou Xinhua, Bao Chenggang, et al. Study on behaviors of Maopingxi Rockfill Dam with asphalt concrete core of Three Gorges Project[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1470–1477. |
| [11] |
熊堃, 何蕴龙, 张艳锋. “5.12”汶川大地震时冶勒大坝实测动力反应[J].
岩土工程学报, 2008, 30(10): 1575–1580.
Xiong Kun, He Yunlong, Zhang Yanfeng. Recorded seismic response of Yele Dam during “5.12” Wenchuan Earthquake[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1575–1580. |
| [12] |
曹学兴, 何蕴龙, 熊堃, 等. 汶川地震对冶勒大坝影响分析[J].
岩土力学, 2010, 31(11): 3542–3548.
Cao Xuexing, He Yunlong, Xiong Kun, et al. Effects of Wenchuan earthquake on Yele Dam[J]. Rock and soil Mechanics, 2010, 31(11): 3542–3548. |
| [13] |
万彪, 何蕴龙, 熊堃. 有厚度节理单元开发与应用[J].
水电能源科学, 2008, 26(4): 63–66.
Wan Biao, He Yunlong, Xiong Kun. Development of joint element with thickness and its application[J]. Water Resources and Power, 2008, 26(4): 63–66. |
| [14] | Bandis S C, Lumsden A C, Barton N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences, 1983, 20(6): 249–268. DOI:10.1016/0148-9062(83)90595-8 |
| [15] | Clough G W, Duncan J M. Finite element analysis of retaining wall behavior[J]. Journal of Soil Mechanics and Foundation Engineering Division, ASCE, 1971, 97(12): 1657–1673. |
 2016, Vol. 49
2016, Vol. 49




