武汉大学学报(工学版)   2016, Vol. 49 Issue (6): 812-817

文章信息

董健, 李典庆, 曹子君, 王宇
DONG Jian, LI Dianqing, CAO Zijun, WANG Yu
确定土性参数标准值的贝叶斯框架及软件实现
Bayesian framework for determining standard values of soil properties and implementation in Excel
武汉大学学报(工学版), 2016, 49(6): 812-817
Engineering Journal of Wuhan University, 2016, 49(6): 812-817
http://dx.doi.org/10.14188/j.1671-8844.2016-06-003

文章历史

收稿日期: 2016-05-16
 Abstract              PDF               Figures               Tables
引用本文 0
董健, 李典庆, 曹子君, 王宇. 确定土性参数标准值的贝叶斯框架及软件实现[J]. 武汉大学学报(工学版), 2016, 49(6): 812-817.
DONG Jian, LI Dianqing, CAO Zijun, WANG Yu. Bayesian framework for determining standard values of soil properties and implementation in Excel[J]. Engineering Journal of Wuhan University, 2016, 49(6): 812-817.
确定土性参数标准值的贝叶斯框架及软件实现
董健1, 李典庆1, 曹子君1, 王宇2     
1. 武汉大学水资源与水电工程科学国家重点实验室, 湖北 武汉 430072;
 2. 香港城市大学深圳研究院土木及建筑工程系,香港 999077
收稿日期: 2016-05-16
作者简介: 董健(1992-)，男，硕士研究生，研究方向为岩土工程不确定性，E-mail: dong-j@foxmail.com.
通讯作者: 曹子君(1987-)，男，副教授，研究方向为岩土工程不确定性分析与风险评价，E-mail: zijuncao@whu.edu.cn
基金项目: 国家杰出青年基金项目(编号：51225903)；国家自然科学基金项目(编号：51409196，51579190，51528901).
摘要: 提出了根据先验信息和较少的勘探数据确定土性参数标准值的贝叶斯框架，该框架对不同的土性参数、勘探数据和转换模型具有广泛的适用性.基于所提出的贝叶斯框架，采用Visual Basic for Applications(VBA)语言开发了岩土工程场地模拟及参数分析软件(WHUGSSPA)，便于工程师应用.最后以砂土有效内摩擦角和标准贯入试验数据为例，利用软件确定的有效内摩擦角的均值和标准差与三轴压缩试验结果相差分别为0和0.1，说明所提方法的有效性和软件的实用性.
关键词： 标准值     不确定性     贝叶斯框架     先验信息     马尔科夫链蒙特卡洛方法    
Bayesian framework for determining standard values of soil properties and implementation in Excel
DONG Jian1, LI Dianqing1, CAO Zijun1, WANG Yu2     
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
 2. Department of Civil and Architecture Engineering, Shenzhen Institute, City University of Hong Kong, Hong Kong 999077, China
Abstract: Standard values of soil properties are usually used as the basic representative values in geotechnical design. It is difficult to determine those standard values because the number of in-situ test data is limited. A Bayesian framework which applies widely to different soil properties, in-situ test data and transformation models is proposed to determine the standard values of soil properties according to test data and prior information. Based on the proposed Bayesian framework, this paper develops the geotechnical site simulation and parameter analysis (WHUGSSPA) using Visual Basic for applications, which is convenient for engineers to use. At last, an example of the effective internal friction angle and standard penetration tests data is given to illustrate the availability of the proposed method and practicability of the software. And little difference (0 and 0.1 for mean and standard deviation) between the results from the software and triaxial compression test.
Key words: standard value     uncertainty     Bayesian framework     prior information     Markov Chain Monte Carlo simulation    

在岩土工程设计以及岩土工程规范中，例如《岩土工程勘察规范》(GB 50021-2001) ，常采用土性参数标准值作为设计中的基本代表值.确定土性参数标准值需要土性参数的统计特征值(如土性参数的均值、标准差、变异系数等)[1-2].然而，在岩土工程勘察过程中获取的勘探数据非常少，采用传统的统计分析方法无法合理地确定土性参数的统计特征和概率分布.因此，在勘探数据非常少的条件下确定土性参数标准值是十分困难的.

贝叶斯方法为解决上述问题提供了一条有效的途径.Wang和Cao[3]提出了根据较少的标准贯入试验数据确定黏性土弹性模量统计特征的贝叶斯方法；Cao和Wang[4]提出了根据较少的含水量数据选择黏性土不排水剪强度概率模型和确定其统计特征的贝叶斯方法；Wang等[5]建立了采用较少的标准贯入试验数据确定砂土有效内摩擦角统计特征的贝叶斯方法.相对于传统统计分析方法，贝叶斯方法能够将先验信息(如工程经验和判断)和较少的勘探数据有效地结合起来，并将结合后的信息转换为大量的等效样本，确定土性参数的统计特征、概率分布和标准值.上述研究中对给定的土性参数和勘探数据开展研究，在贝叶斯分析中具体的算法与土性参数、勘探数据以及它们之间的相互关系(即转换模型)有关，亟需发展广泛适用于多种土性参数、勘探数据和转换模型的贝叶斯框架.此外，贝叶斯方法相对于传统的统计分析方法更加复杂，在实际应用中受到限制，需要发展有效的实用工具辅助工程师进行贝叶斯参数分析.

本文提出了具有广泛适用性的贝叶斯框架，根据非常少的勘探数据确定土性参数标准值.基于所提出的贝叶斯框架，采用Visual Basic for Applications(VBA)语言开发了岩土工程场地模拟及参数分析软件(WHUGSSPA)，软件中内置了7种土性参数、6种勘探数据和12个转换模型.此外，用户可以根据需要自定义土性参数、勘探数据和转换模型.最后，采用WHUGSSPA分析了在加拿大米尔德里湖地区砂土中测量的标准贯入试验数据，确定其有效内摩擦角统计特征、概率分布和标准值，说明了所提方法的有效性和软件的实用性.

1 有限数据条件下确定土性参数标准值的贝叶斯框架 1.1 土性参数的概率分布

土性参数标准值常取其概率分布的某分位值(如5%的分位值).对于给定的一套勘探数据Data=Di(i=1, 2, …, n)和先验信息Prior，土性参数X的概率分布为f(X|Data, Prior).根据全概率定理，f(X|Data, Prior)表达为[3-6]

$\begin{align} & f(X|Data,Prior)= \\ & \text{ }\int_{\mu ,\sigma }{f(X|\mu ,\sigma )}f(\mu ,\sigma |Data,Prior)d\mu d\sigma \\ \end{align}$    (1)

式中: μ和σ为土性参数X的均值和标准差；f(X|μ, σ)为给定一组均值和标准差条件下土性参数X的概率分布；f(μ, σ|Data, Prior)是给定勘探数据和先验数据条件下均值和标准差的联合概率分布.由于土体是一种天然材料，受复杂地质成因的影响，土体性质存在内在的变异性.这种内在变异性可以用随机变量来表征，常见的表征土性参数的分布类型包括正态分布和对数正态分布.对于服从正态分布的土性参数，其概率分布为[7]

$f(X|\mu ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma }\exp \left\{ -\frac{1}{2}\mathop{\left[ \frac{X-\mu }{\sigma } \right]}^{2} \right\}$    (2)

对于服从对数正态分布的土性参数，其概率分布为

$f(X|\mu ,\sigma )=\frac{1}{\sqrt{2\pi }{{\sigma }_{N}}X}\exp \left\{ -\frac{1}{2}\mathop{\left[ \frac{\ln (X)-{{\mu }_{N}}}{{{\sigma }_{N}}} \right]}^{2} \right\}$    (3)

式中: ${{\mu }_{N}}=\ln \mu -\sigma _{N}^{2}/2,{{\sigma }_{N}}\text{=}\sqrt{\ln (1+{{(\sigma /\mu )}^{2}})}$，分别为lnX的均值和标准差.

1.2 贝叶斯框架

根据贝叶斯定理，在给定一套勘探数据和先验信息条件下，f(μ, σ|Data, Prior)表示为[3, 6]

$\begin{align} & f(\mu ,\sigma |Data,Prior)= \\ & \text{ }f(\mu ,\sigma |Data)=Kf(Data|\mu ,\sigma )f(\mu ,\sigma ) \\ \end{align}$    (4)

式中: f(μ, σ)为μ和σ的先验分布；K=(∫μ, σP(Data|μ, σ)P(μ, σ)dμdσ)-1，是一个与μ和σ无关的归一化常量.

将式(4) 代入式(1) 可得:

$\begin{align} & f(X|Data,Prior)= \\ & \text{ }K\int_{\mu ,\sigma }{f(X|\mu ,\sigma )}f(Data|\mu ,\sigma )f(\mu ,\sigma )d\mu d\sigma \\ \end{align}$    (5)

求解式(5) 需要先验分布f(μ, σ)和似然函数f(Data|μ, σ).先验分布依赖于先验信息，常见的先验分布类型包括: 均匀分布、正态分布、三角分布等.如公式(4) 中f(μ, σ)可采用均匀分布作为先验分布，f(μ, σ)可表示为

$f(\mu ,\sigma )=\left\{ \begin{matrix} \frac{1}{{{\mu }_{\max }}-{{\mu }_{\min }}\times {{\sigma }_{\max }}-{{\sigma }_{\min }}} & \begin{matrix} \mu \in \text{(}{{\mu }_{\min }},{{\mu }_{\max }}\text{)} \\ \sigma \in \text{(}{{\sigma }_{\min }},{{\sigma }_{\max }}\text{)} \\ \end{matrix} \\ 0 & 其他 \\ \end{matrix} \right.$    (6)

式中: μmin和μmax分别为μ的最小值和最大值；σmin和σmax分别为σ的最小值和最大值.

在岩土工程勘察中，测量参数通常不是最终设计中采用的设计参数，设计参数通常由测量参数经转换模型计算而来，表 1列出了文献中常见的12条转换模型，它们均可以表示成如下形式:

$D=a{{X}^{'}}+b+\varepsilon $    (7)

式中: D为测量参数或测量参数的函数；X′为设计参数X或其对数lnX；a和b为转换模型参数；ε是一个高斯型随机变量，表征了转换模型的不确定性，其平均值为με，标准差为σε.根据X′的形式可选用不同的分布类型来表征设计参数的内在变异性，见表 1中最后一列.

如X服从正态分布，则[7]:

${{X}^{'}}=X=\mu +\sigma z$    (8)

式中: z是一个标准正态随机变量.

将式(8) 代入式(7) 可知，D为服从均值为aμ+b+με和标准差为$\sqrt{\mathop{\left( a\sigma \right)}^{2}+\mathop{\sigma }_{\varepsilon }^{2}}$的正态分布[5], 则似然函数可以表达为

$\begin{align} & f(Data|\mu ,\sigma )=\prod\limits_{i=1}^{n}{\frac{1}{\sqrt{2\pi }\sqrt{\mathop{\left( a\mathop{\sigma }^{{}} \right)}^{2}+\mathop{\sigma }_{\varepsilon }^{2}}}\times } \\ & \text{ }\exp \left\{ -\frac{1}{2}\mathop{\left[ \frac{\mathop{D}_{i}-(a\mathop{\mu }^{{}}+b+{{\mu }_{\varepsilon }})}{\sqrt{\mathop{\left( a\mathop{\sigma }^{{}} \right)}^{2}+\mathop{\sigma }_{\varepsilon }^{2}}} \right]}^{2} \right\} \\ \end{align}$    (9)

如X服从对数正态分布，则[3, 7]:

${{X}^{'}}=\ln X={{\mu }_{N}}+{{\sigma }_{N}}z$    (10)

将式(10) 代入式(7) 可知，D为服从均值为aμN+b+με和标准差为$\sqrt{\mathop{\left( a{{\sigma }_{N}} \right)}^{2}+\mathop{\sigma }_{\varepsilon }^{2}}$的正态分布，则似然函数可以表达为

$\begin{align} & f(Data|\mu ,\sigma )=\prod\limits_{i=1}^{n}{\frac{1}{\sqrt{2\pi }\sqrt{\mathop{\left( a{{\sigma }_{N}} \right)}^{2}+\mathop{\sigma }_{\varepsilon }^{2}}}}\times \\ & \text{ }\exp \left\{ -\frac{1}{2}\mathop{\left[ \frac{\mathop{D}_{i}-(a{{\mu }_{N}}+b+{{\mu }_{\varepsilon }})}{\sqrt{\mathop{\left( a{{\sigma }_{N}} \right)}^{2}+\mathop{\sigma }_{\varepsilon }^{2}}} \right]}^{2} \right\} \\ \end{align}$    (11)

本文采用马尔科夫链蒙特卡洛方法(MCMCS)，根据公式(5) 产生大量的土性参数X的样本，基于这些样本可以得到X的概率分布和标准值.MCMCS方法是用来模拟随机变量的样本序列的数值过程.该样本序列服从马尔科夫性质，并且随机变量的概率密度就是马尔科夫链的平稳分布[3].对于任意的概率密度函数，尤其像公式(5) 这样的形式复杂、难以用解析形式表达的概率密度函数，MCMCS非常适用.由于篇幅限制，本文不展开介绍MCMCS，具体的MCMCS算法可以参阅文献[3, 10, 11].

表 1 12个常见的转换模型 Table 1 Twelve familiar transformation models
序号设计参数测量参数转换模型输入量分布类型
黏性土1杨氏模量Eu/kPaNSPTlnNSPT=1.587lnEu-1.044+εNSPT对数正态
2LILI=-0.268lnSu+1.514+εLI对数正态
3不排水剪强度Su/kPaKDlnKD=0.806ln(Su/σ′v)+1.71+εKD对数正态
4NSPTlnNSPT=1.388 9lnSuUU-4.676 8+εNSPT对数正态
5PIln(0.11+0.003 7PI)=ln(Su/σp)+ε0.11+0.003 7PI对数正态
6有效内摩擦角φ′/(°)PIlnPI=-10.638φ′+8.510 6+εPI对数正态
7原位水平应力系数KDKD=3.703 7K0+εKD正态
8K0NSPTNSPT/σ′v=0.137K0+εNSPT/σ′v正态
砂砂土9有效内摩擦角φ′/(°)qc$\ln \left( \frac{{\mathop{q}_{c}}/{\mathop{p}_{a}}\;}{\sqrt{{\mathop{\sigma }_{v}^{'}}/{\mathop{p}_{a}}\;}} \right)=0.209\mathop{\phi }^{'}-3.68+\varepsilon $$\frac{{\mathop{q}_{c}}/{\mathop{p}_{a}}\;}{\sqrt{{\mathop{\sigma }_{v}^{'}}/{\mathop{p}_{a}}\;}}$正态
10NSPTln(N1)60=0.161φ′-3.724+ε(N1)60正态
11杨氏模量EPMT/kPaNSPTN0.66=1.1EPMT+εN0.66正态
12杨氏模量ED/kPaNSPTlnN=1.22lnED-0.962+εNSPT对数正态
注: 资料来源于文献[3, 4, 5, 8, 9]；σ′v为竖向有效应力，kPa；σp为预固结应力，kPa；pa为标准大气压强，100 kPa；UU表示不固结不排水三轴试验；PMT表示旁压试验；KD为由膨胀仪测得的水平应力系数;PI为塑性指数；LI为液性指数；qc为静力触探锥尖阻力.
表选项
2 基于Excel的WHUGSSPA软件

为了方便岩土工程领域人员使用本方法，本文基于Excel的VBA语言开发了岩土工程场地模拟及参数分析软件(WHUGSSPA)，软件共有场地模拟和参数分析两个模块.其中参数分析模块所采用的即是本文提出的方法，场地模拟所解决的问题不在本文讨论的范围之内.

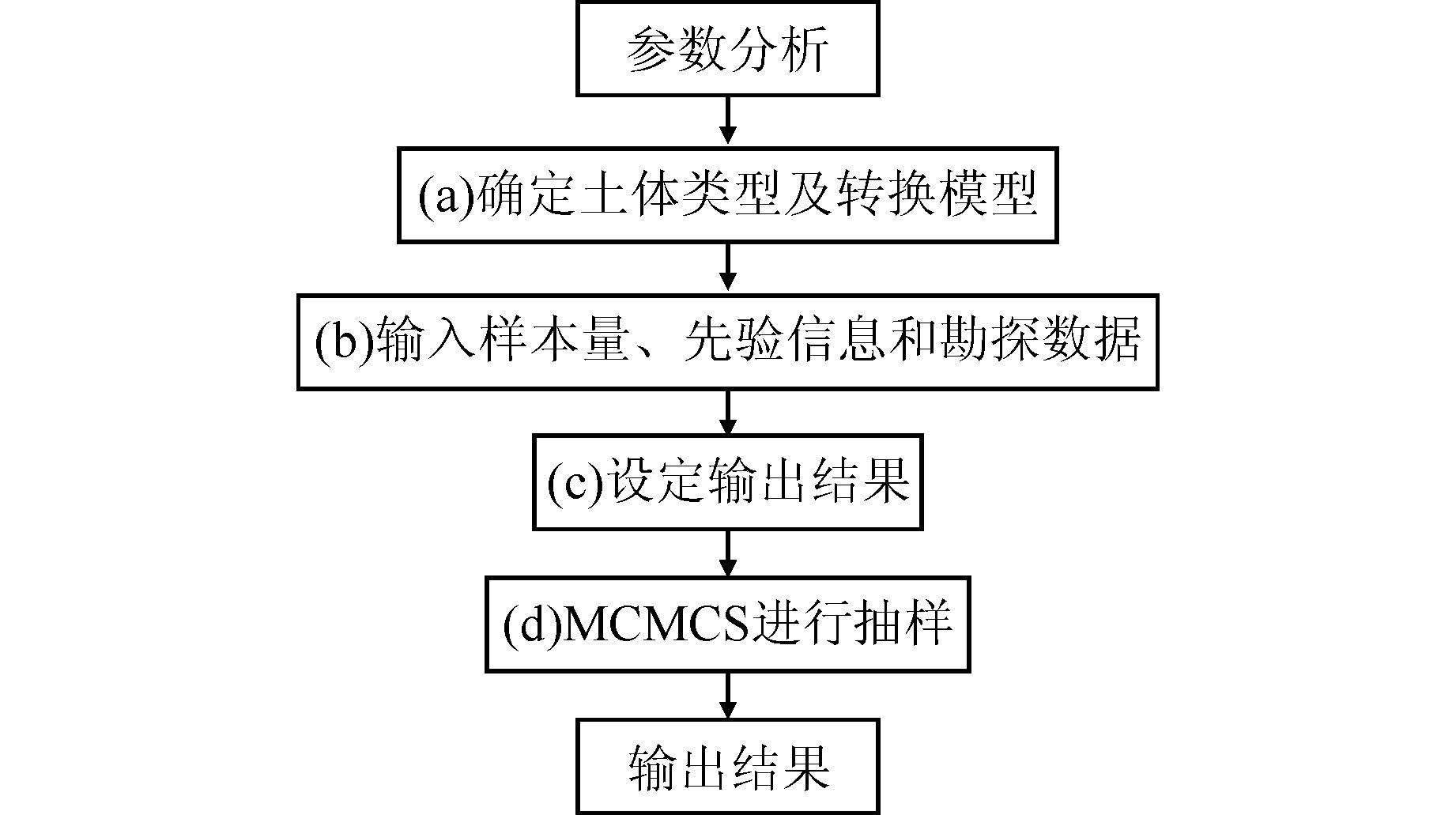
图 1所示为软件“参数分析”部分的计算流程图，其中a、b两个部分为软件的输入部分，输入的信息主要包括: 土体类型、转换模型、先验信息、MCMCS样本量和勘探数据等.图 2给出了设置转换模型的界面示意图.软件内置了表 1中常见的12个转换模型，并支持用户自定义(见图 2)线性转换模型(如公式(7) )，极大地扩展了软件的应用范围.12个转换模型在软件中需要输入的测量数据可以参照表 1中“输入量”一列.

图 1 “参数分析”模块流程图 Figure 1 Flowchart for module parameters analysis
图选项
图 2 设置转换模型的界面 Figure 2 Interface for setting transformation model
图选项

流程图中步骤c为设定软件的输出结果，可选的结果包括: 土性参数分布的统计特征(均值、标准差)、样本直方图和散点图、土性参数的概率密度函数曲线和累积概率分布曲线.完成输入项和输出项设定后，软件采用MCMCS产生大量的服从公式(5) 分布的土性参数的样本，并提供预先设定的输出项结果，将在下一节中通过实际勘探数据进一步说明WHUGSSPA的有效性与实用性.

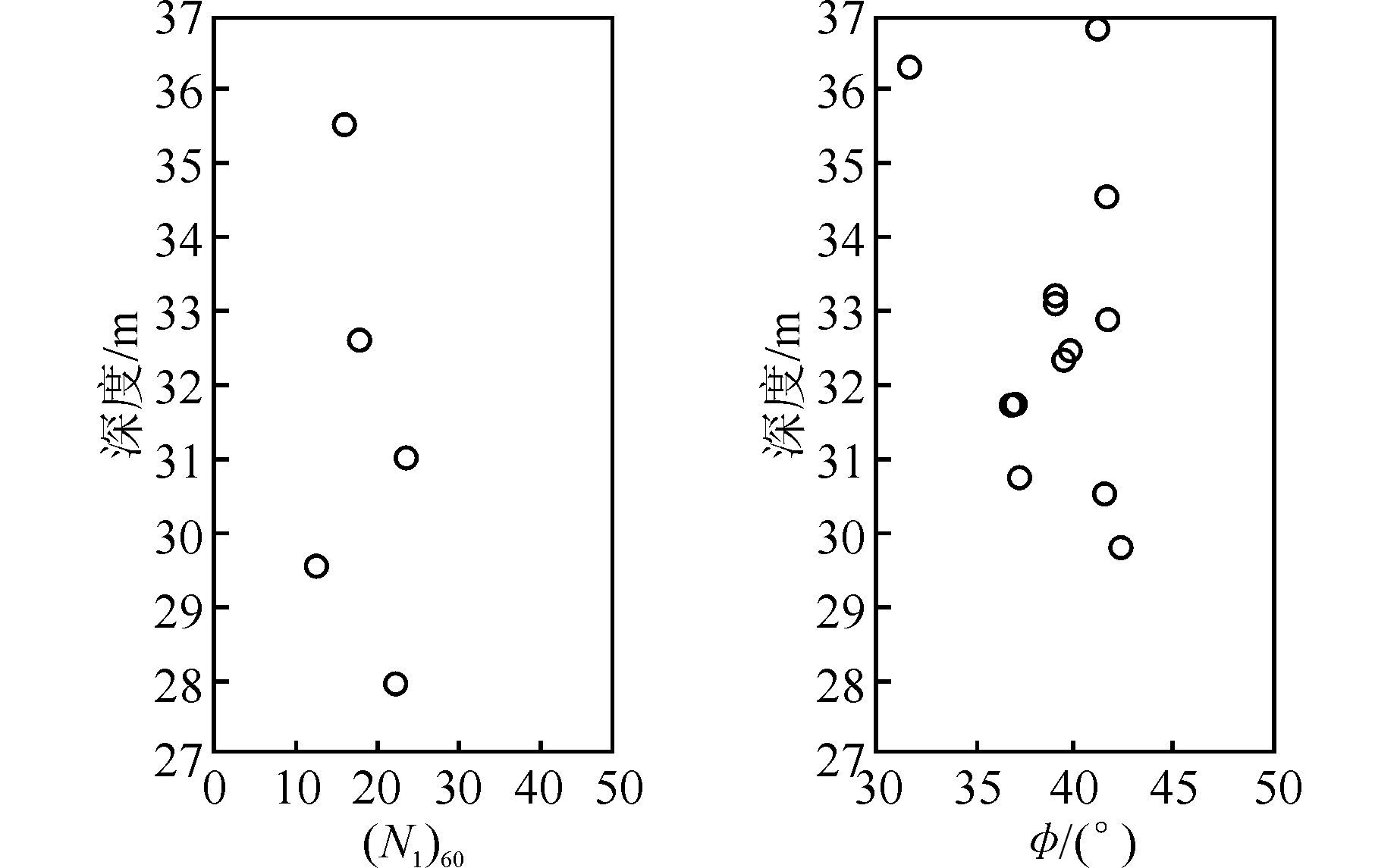
3 算例分析

本算例采用位于加拿大阿尔伯塔省麦克默里堡北部米尔德里湖地区的砂土层数据[5].该地区砂土层大致位于地表以下27~37 m，厚度为10 m.图 3(a)是在该砂土层中采用标准贯入试验(SPT)测得的5个修正后的锤击次数值(N1)60.图 3(b)所示为根据室内三轴试验测得的13个有效内摩擦角值.13个有效内摩擦角的均值为38.9°，标准差为3.0°.Wang等[5]利用上述数据研究了砂土有效内摩擦角统计特征的贝叶斯确定方法.本算例使用5个SPT数据作为软件的输入数据，13个直接测量的有效内摩擦角及其统计特征值则用来作为验证数据，检验软件计算结果的有效性.

图 3 SPT数据、(N1)60和有效内摩擦角φ′[5] Figure 3 SPT data, (N1)60and effective internal friction angle φ′
图选项

由表 1可知SPT数据(N1)60和砂土有效内摩擦角之间的一个转换模型如下:

$\ln {{({{N}_{1}})}_{60}}=0.161\mathop{\phi }^{'}-3.724+\varepsilon $    (12)

式(12) 中模型误差ε是一个服从正态分布的随机变量，均值为0，标准差为0.496.由表 1知，采用正态随机变量表征有效内摩擦角的内在变异性(即式(8) )，将其均值μ和标准差σ的先验分布考虑成联合均匀分布(即式(6) )，均值的范围为(20°，40°)，标准差的范围为(1°，6°)[5].基于上述输入信息(包括图 3(a)中的SPT数据、公式(12) 和先验信息)，采用WHUGSSPA产生了30 000个φ′的等效样本.

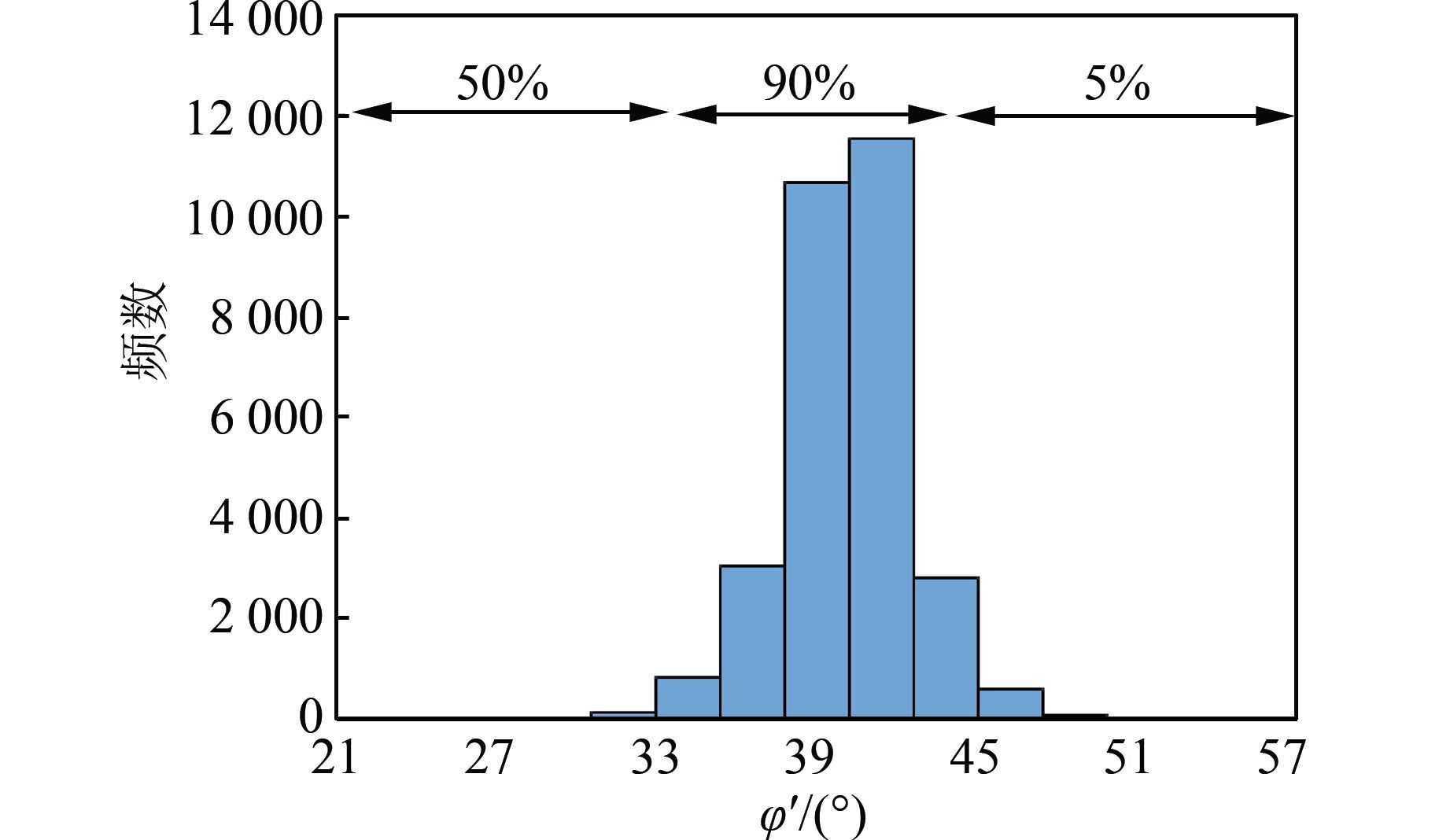
图 4为根据30 000个样本得到直方图，图 4所示有效内摩擦角的最可能值约为39°.30 000个样本中有27 000个样本(90%)落在了(33.6°, 43.8°)之间，有1 500个样本(5%)小于33.6°，1 500个样本(5%)大于43.8°.若采用5%的分位值作为设计标准值，则φ′的标准值取为33.6°.

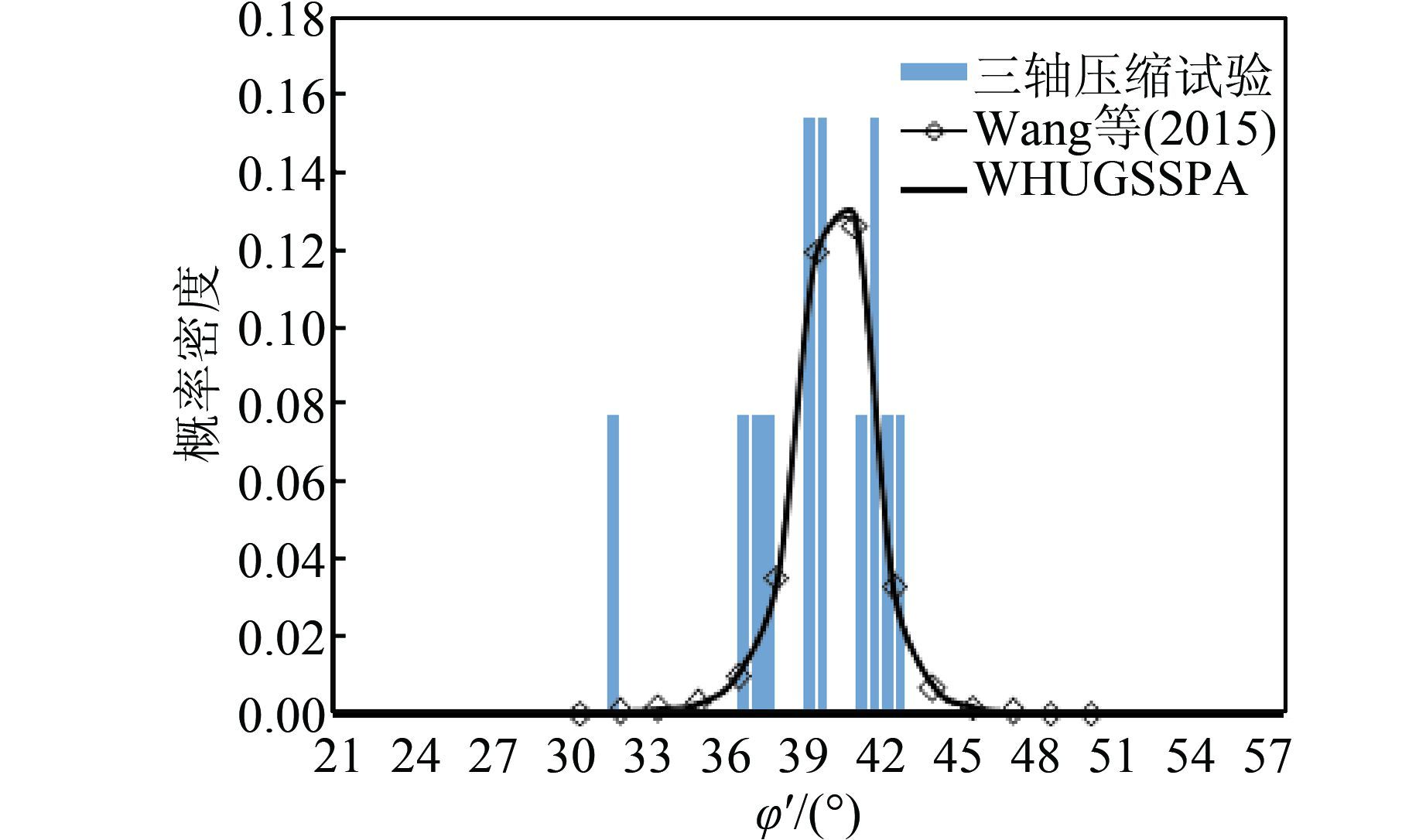
图 5所示为根据30 000个MCMCS样本所绘制的有效内摩擦角的概率密度函数曲线.WHUGSSPA给出的概率密度函数曲线与Wang等[5]计算的结果基本一致，同时以直方图的形式将三轴压缩数据绘制在图 5中，可见三轴压缩数据基本落在(33.6°, 43.8°)这一范围，说明了WHUGSSPA的准确性.

图 4 有效内摩擦角的直方图 Figure 4 Histogram of effective internal friction angle
图选项
图 5 有效内摩擦角的概率密度曲线 Figure 5 Probability density curve for effective internal friction angle
图选项

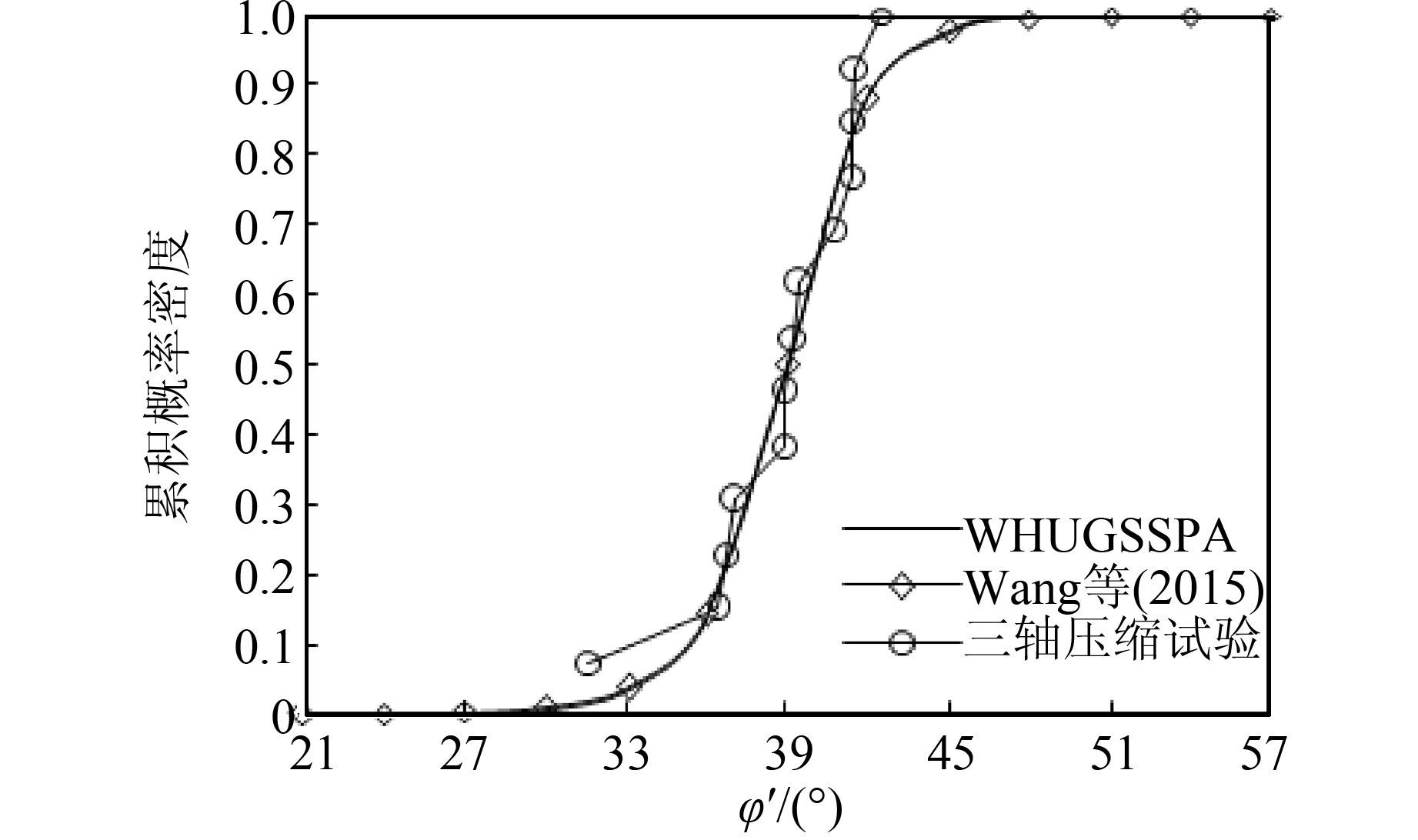
图 6对比了根据30 000个MCMCS样本得到的累积概率分布曲线、Wang等[5]计算的累积概率分布曲线和根据13个室内三轴试验数据得到的累积概率分布曲线.从图中可以看出，将先验信息和有限的SPT数据结合起来得到的结果与室内三轴试验数据基本一致，验证了所提出的贝叶斯框架的有效性.表 2给出了3种方法对应的有效内摩擦角的均值和标准差，根据WHUGSSPA产生的30 000个MCMCS样本得到的均值和标准差与根据室内三轴试验得到的结果以及Wang等[5]的结果基本一致，进一步表明了所提出的贝叶斯框架和WHUGSSPA的有效性.

图 6 有效内摩擦角的累积概率分布曲线 Figure 6 Cumulative probability distribution curves of effective internal friction angle
图选项
表 2 有效内摩擦角的均值和标准差 Table 2 Mean value and standard deviation of effective internal friction angle
方法WHUGSSPAWang等(2015) 三轴压缩试验
均值/(°)38.938.838.9
标准差/(°)3.13.23.0
表选项
4 结论

本文提出了根据先验信息和非常少的勘探数据确定土性参数标准值的贝叶斯框架，该框架对不同土性参数、勘探数据和转换模型具有广泛的适用性.基于所提出的贝叶斯框架，采用VBA语言开发了岩土工程场地模拟及参数分析软件(WHUGSSPA)，该软件目前内置了7种土性参数、6种勘探数据和12个转换模型，并允许用户自定义不同土性参数、勘探数据和转换模型.通过对比实际勘探数据的计算结果和文献中的结果以及室内试验数据结果，说明了所提贝叶斯框架和WHUGSSPA软件的有效性和实用性，为勘探数据非常少的条件下确定土性参数标准值提供了一条可行的途径.

参考文献
[1] 中华人民共和国住房和城乡建设部. GB 50021-2001 岩土工程勘察规范[S]. 北京: 中国建筑工业出版社, 2009.
Ministry of Housing and Urban-Rural Development of the People`s Republic of China. GB 50021-2001 Code for Investigation of Geotechnical Engineering[S]. Beijing: China Architecture & Building Press, 2009.
[2] 熊敏, 蒋水华, 李典庆. 中国与欧洲规范关于坝坡抗滑稳定分析方法的比较[J]. 武汉大学学报(工学版), 2013, 46(5): 593–598.
Xiong Min, Jiang Shuihua, Li Dianqing. A comparative investigation on slope stability analysis of embankment dams between Chinese and European geotechnical design codes[J]. Engineering Journal of Wuhan University, 2013, 46(5): 593–598.
[3] Wang Yu, Cao Zijun. Probabilistic characterization of Young’s modulus of soil using equivalent samples[J]. Engineering Geology, 2013(159): 106–118.
[4] Cao Zijun, Wang Yu. Bayesian model comparison and characterization of undrained shear strength[J]. Journal of Geotechnical and Environmental Engineering, 2014, 140(6): 04014018. DOI:10.1061/(ASCE)GT.1943-5606.0001108
[5] Wang Yu, Zhao Tengyuan, Cao Zijun. Site-specific probability distribution of geotechnical properties[J]. Computers and Geotechnics, 2015, 70: 159–168. DOI:10.1016/j.compgeo.2015.08.002
[6] 曹子君, 赵腾远, 王宇, 等. 基于贝叶斯等效样本的土体杨氏模量的统计特征确定方法[J]. 防灾减灾工程学报, 2015, 35(5): 581–585.
Cao Zijun, Zhao Tengyuan, Wang Yu, et al. Characterization of Young’s modulus of soil using Bayesian equivalent samples[J]. Journal of Disaster Prevention and Mitigation Engineering, 2015, 35(5): 581–585.
[7] Ang AH-S, Tang W H. Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering[M]. New York: John Wiley, 2007.
[8] Phoon K K, Kulhawy F H. Evaluation of geotechnical property variability[J]. Canadian Geotechnical Journal, 1999, 36: 625–639. DOI:10.1139/t99-039
[9] Ohya S, Imai T, Matsubara M. Relationship between N value by SPT and LI T pressuremeter results[C]// Proceedings of 2nd European Symposium on Penetration Testing, 1982, 1: 125-130.
[10] Beck J L, Au S K. Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation[J]. Journal of Engineering Mechanics, 2002, 128(4): 380–391. DOI:10.1061/(ASCE)0733-9399(2002)128:4(380)
[11] 熊立华, 卫晓婧, 万民. 水文模型两种不确定性研究方法的比较[J]. 武汉大学学报(工学版), 2009, 42(2): 137–142.
Xiong Lihua, Wei Xiaojing, Wan Min. Comparison between GLUE and MCMC methods for estimating hydrological model uncertainty[J]. Engineering Journal of Wuhan University, 2009, 42(2): 137–142.