文章信息
- 杜国锋, 何明星, 吴方红, 别雪梦
- DU Guofeng, HE Mingxing, WU Fanghong, BIE Xuemeng
- 动荷载作用下的智能骨料力电效应仿真分析
- Simulation analysis of mechano-electric effect of smart aggregate under dynamic loading
- 武汉大学学报(工学版), 2016, 49(4): 572-576
- Engineering Journal of Wuhan University, 2016, 49(4): 572-576
- http://dx.doi.org/10.14188/j.1671-8844.2016-04-015
-
文章历史
- 收稿日期: 2015-05-10
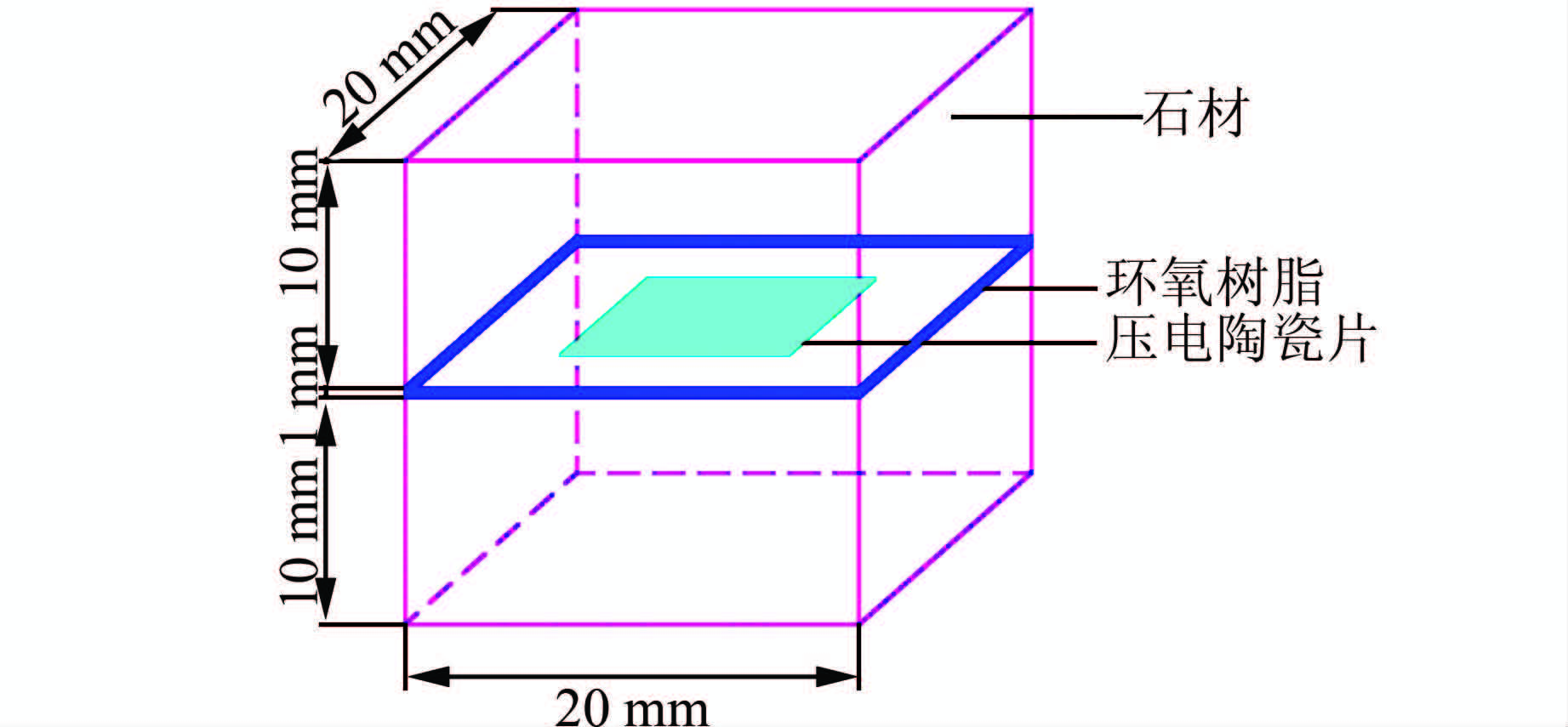
当沿着压电陶瓷片一定方向施加外荷载时,其内部就产生极化现象,同时在它的2个表面产生极性相反的电荷;当外力去除以后,其又重新恢复为不带电的状态,当外力改变方向时,电荷的极性也随之改变,这种现象称为压电陶瓷片的“正压电效应”[1~3],可以利用压电陶瓷的这一特点建立外荷载与输出电压的关系,进而设计制作传感器.由于压电陶瓷类材料材质较脆,防水性能差,曝露在空气中极易氧化,很难单独使用,因此,Song[4, 5]提出将压电陶瓷片封装在水泥块内形成“智能骨料”,并将其应用到混凝土结构健康监测研究当中,Li[6]和Yang等[7]利用压电陶瓷正压电效应原理,将压电智能骨料应用到结构的压应力监测当中,侯爽等[8]则将其应用到路面动态荷载监测当中,但由于水泥块这种封装材料的强度较低从而低限制了此类智能骨料的应用.本文试图利用环氧树脂将d33型压电陶瓷片进行防水和绝缘处理后封装在大理石内,形成大理石基“智能骨料”,并将其埋置在混凝土结构内,利用压电陶瓷的正压电效应可以实现混凝土结构内部动应力的实时监测,其模型如图 1所示.为了解智能骨料在单向动力荷载作用下的工作机理和性能,先进行理论分析和数值模拟计算,其结果将为制作实物模型提供依据.
|
| 图 1 压电智能骨料模型图 Figure 1 Piezoelectric smart aggregate model |
“智能骨料”内d33型压电陶瓷片的尺寸是10 mm×10 mm×0.4 mm,大理石块的尺寸是20 mm×20 mm×10 mm,环氧树脂层厚度为1 mm,压电智能骨料在单向外动应力作用下工作的核心是压电陶瓷电压的变化,而压电陶瓷在线弹性范围类的正压电效应方程为[9, 10]
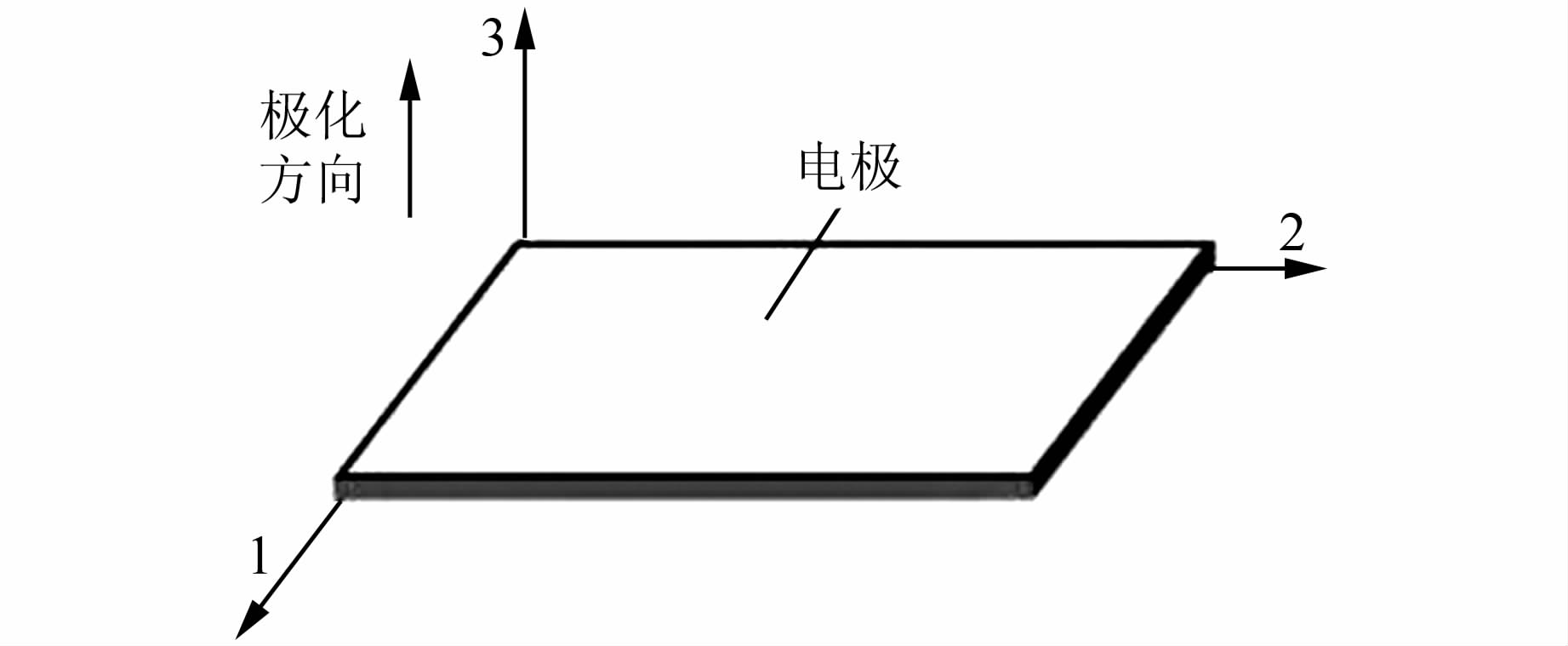
式中:D为电位移向量(3×1);eσ为自由介电常数矩阵(3×3);E为输入电场强度向量(3×1);dd为压电应变常数矩阵(6×3).模拟的d33型压电陶瓷片极化方向如图 2所示,极化方向为厚度方向.在模拟动力荷载与压电陶瓷片电压幅值的关系时,假设输入外电场强度为0,则式(1)可进一步简化为
|
| 图 2 压电陶瓷片及其极化方向示意图 Figure 2 Piezoelectric ceramic chip and its polarization direction |
式中:σ1、σ2和σ3分别是1、2和3方向的应力;σ4、σ5和σ6分别为2-3平面、1-3平面及1-2平面内的剪应力;压电常数d31、d32和d33代表 1、2和3方向的单位应力在3方向产生的电荷量;压电常数d24和d15分别代表 23平面和1-3平面的单位剪应力在1、2方向产生的电荷量.
电位移与产生的电荷量的关系为
其中:dA1、dA2以及dA3分别为2-3、1-3和1-2平面面积的积分.由于1和2两个方向的面积远小于3方向的面积,则忽略1、2方向面积上的电荷量,所以压电陶瓷片在受到沿极化方向的动荷载时产生的总电荷量为
当在压电智能骨料上表面施加均布作用力时,压电陶瓷表面产生的单位面积电荷量为
压电陶瓷片的输出电压与受动荷载作用时产生的电荷量的关系为
式中:c为压电陶瓷固有电容.
压电智能骨料在受到动荷载作用时压电陶瓷片的输出电压的与动荷载的比值定义为压电陶瓷片对外荷载σ的灵敏度,用S表示:
则压电陶瓷的输出电压与动荷载的比值关系关系可简化为
忽略外荷载通过应力波传递到压电陶瓷表面的损失时,认为σ3≈σ,式(8)可进一步简化:
模拟的压电陶瓷片的压电常数d33=272pc/N,电容c=1.5 nF,根据式(9)可以计算出理论上的S值为1.8×10-5V/Pa.
2 智能骨料的有限元模拟 2.1 建立有限元模型利用ABAQUS6.10进行数值模拟,建立4个部件,分别为2块封装大理石材、环氧树脂层和压电陶瓷片,各种材料的参数如表 1所示.模拟压电陶瓷片时,需要使用3个矩阵来对压电陶瓷材料的属性进行定义,分别为弹性常数矩阵、压电应力常数矩阵和相对介电常数矩阵[11~13].
| 材料 | 大理石材 | 环氧树脂 |
| 弹性模量/GPa | 48 | 4 |
| 泊松比 | 0.3 | 0.35 |
弹性常数矩阵:
压电应力常数矩阵:
相对介电常数矩阵ε/ε0:
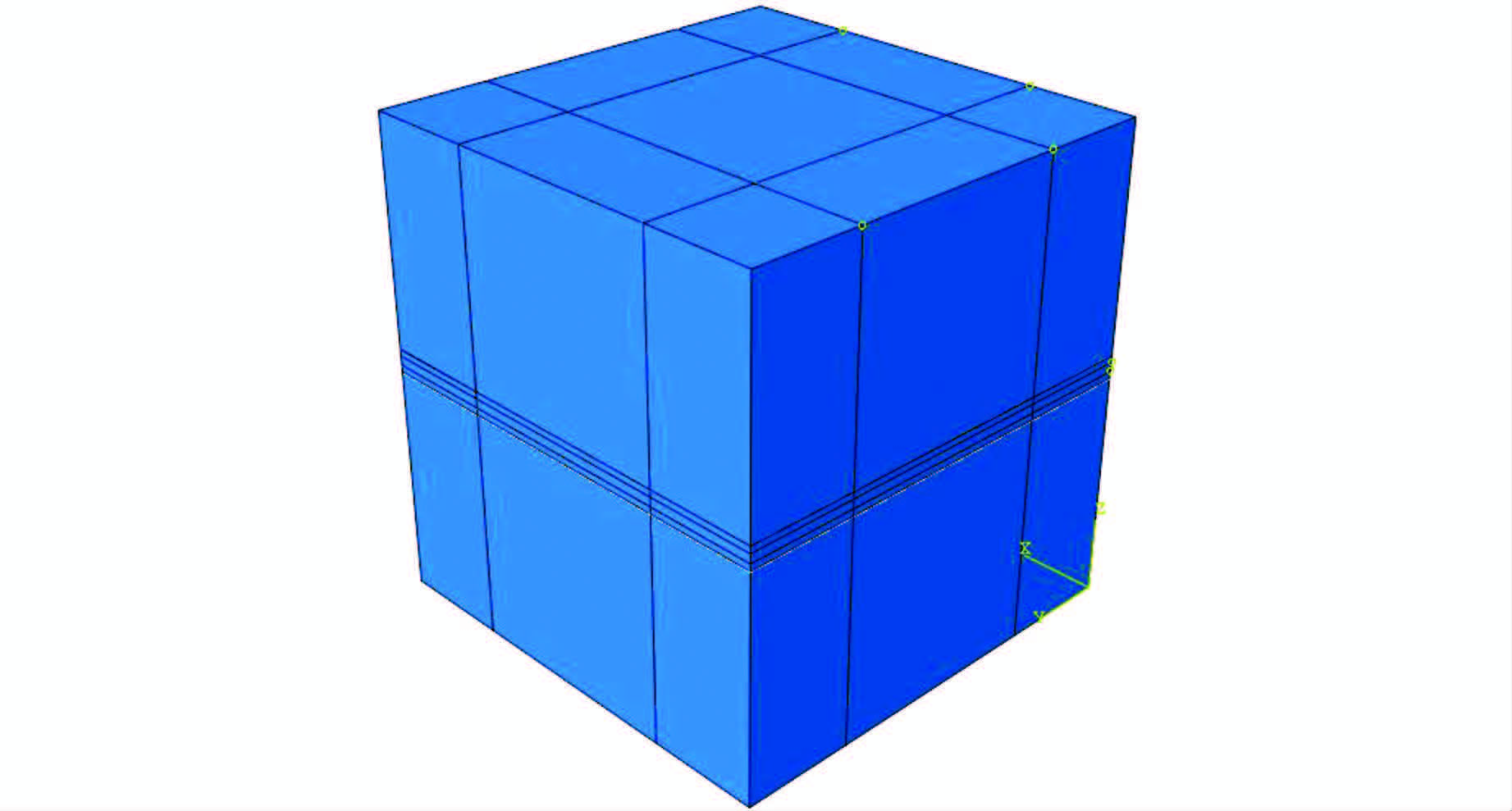
将各部件的属性定义完成后,由于压电材料不是各项同性的,有限元模拟必须通过指派材料方向来定义局部坐标系进而指定其极化方向,最后对4个部件进行装配,装配完成后的智能骨料三维模型如图 3所示,使用8节点的C3D8E线性压电单元模拟压电陶瓷,石材与环氧树脂层均选取C3D8R单元,网格划分模型如图 4所示.
|
| 图 3 智能骨料三维模型图 Figure 3 Smart aggregate three-dimensional model diagram |

|
| 图 4 智能骨料网格划分图 Figure 4 Smart aggregate meshing diagram |
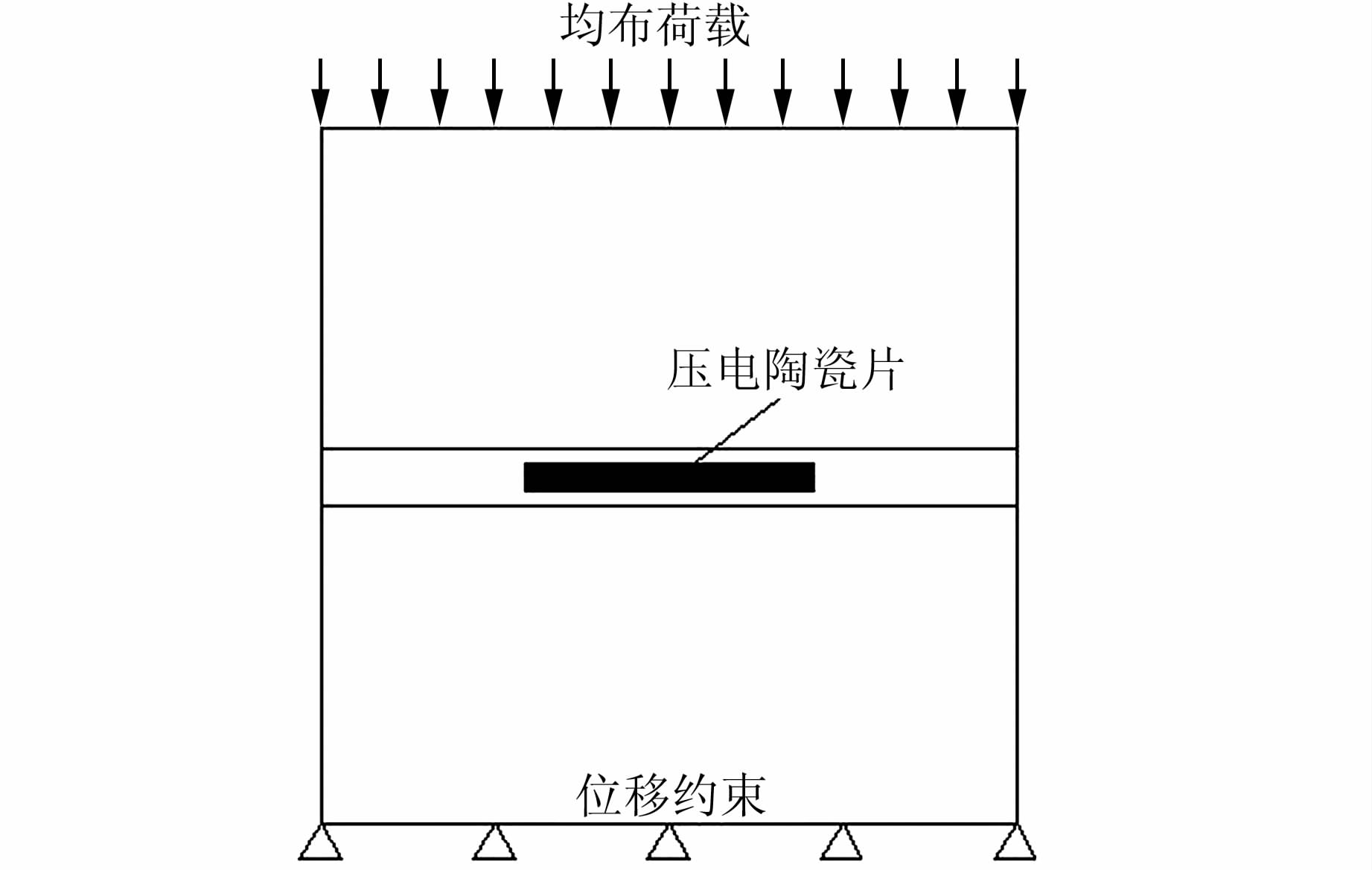
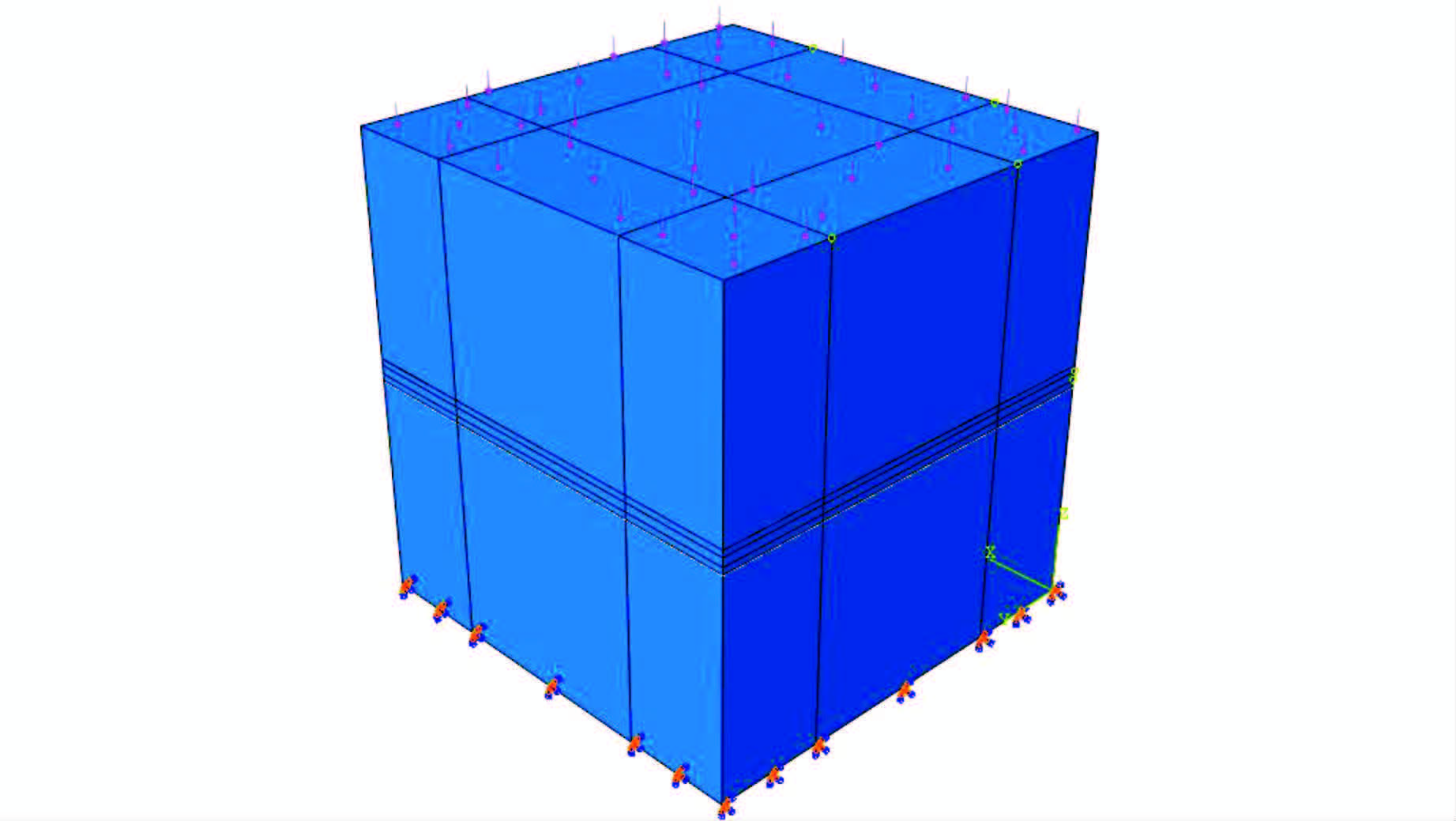
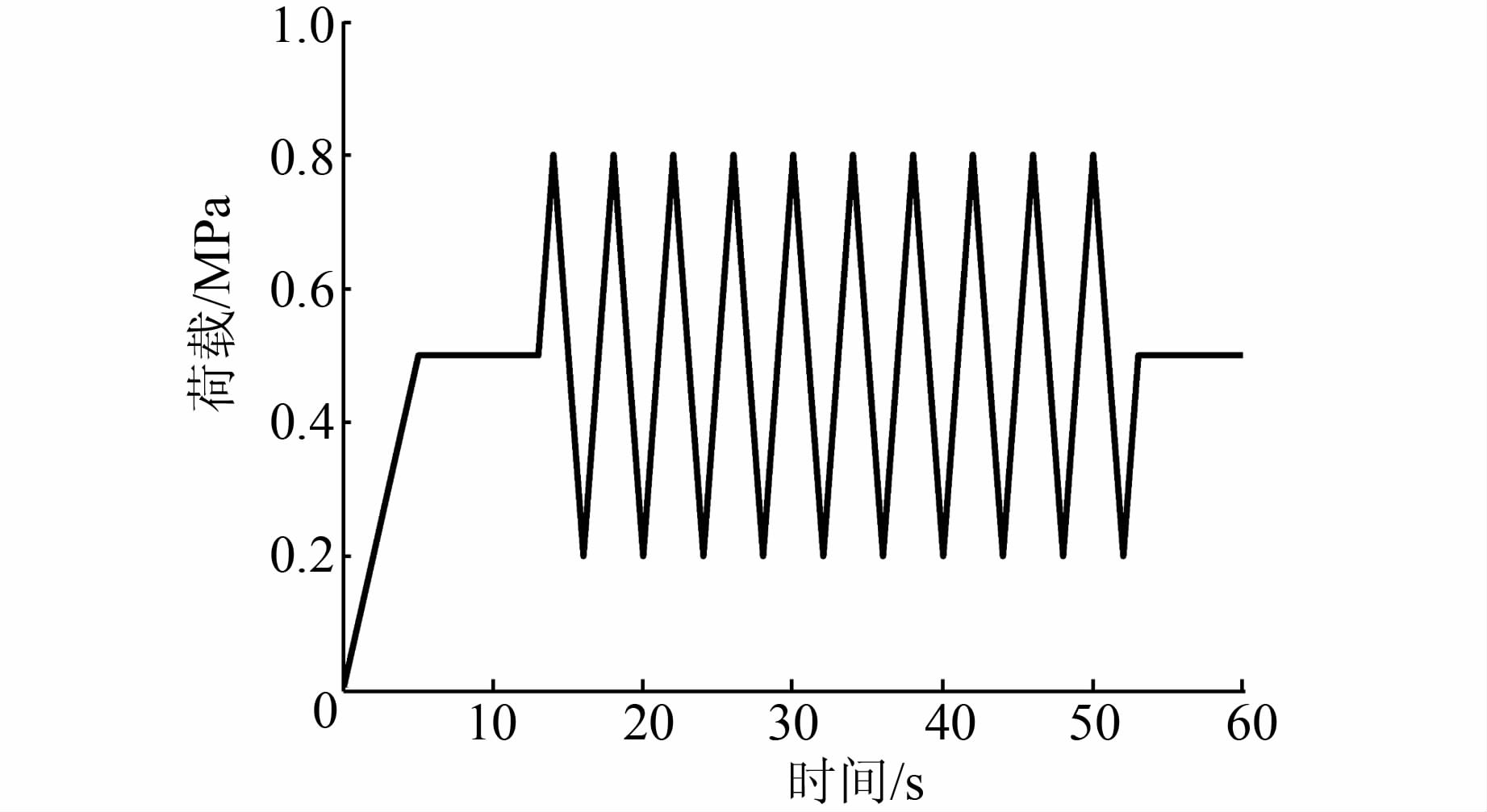
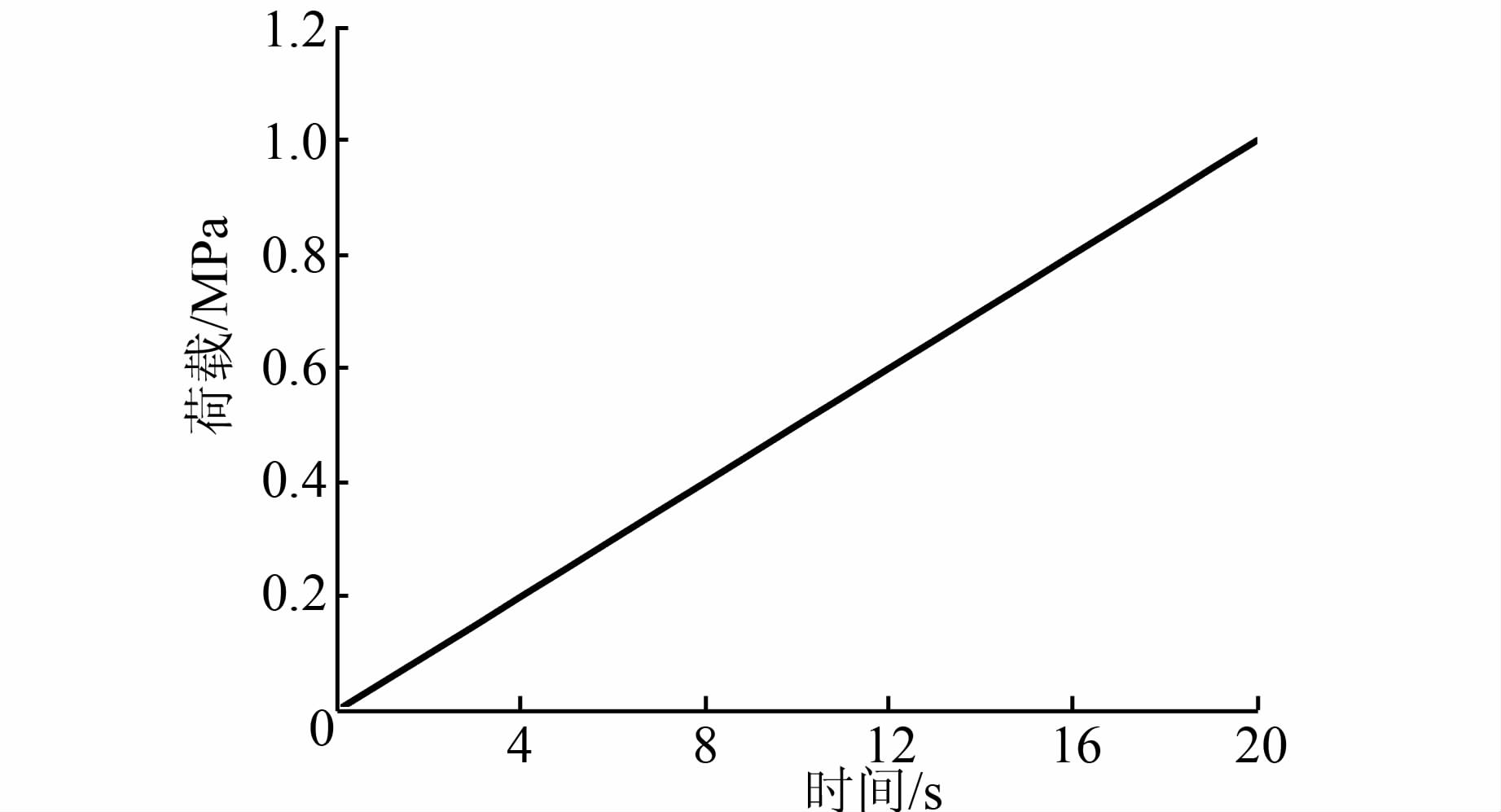
将部件装配完成后,为能够真实地模拟智能骨料在动荷载作用下的工作情况,需要对各组成部件定义相互作用,环氧树脂层与大理石材采用绑定(TIE)约束,压电片与环氧树脂采用内置约束(Embedded Region).在压电智能骨料底面施加X、Y和Z 3方向的局部位移约束,在压电智能骨料上表面施加竖向均布动荷载,其剖面示意如图 5所示;在压电智能骨料三维模型上施加边界条件和动荷载后的示意图如图 6所示.“智能骨料”所受动荷载的类型不同其加载方式也不同.为得到压电陶瓷在动荷载作用下的电压幅值与动荷载的关系,同时检验电压幅值与动荷载之间是否存在滞延现象,采取2种加载方案:第1种加载采用等幅加载,检验滞延性,如图 7所示;第2种加载采取线性加载,检验电压幅值与动荷载之间的变化关系,如图 8所示.
|
| 图 5 边界条件与加载平面示意图 Figure 5 Boundary conditions and loading plan sketch |
|
| 图 6 有限元三维模型边界条件与载荷示意图 Figure 6 Boundary conditions and load diagram of finite element three-dimensional model |
|
| 图 7 等幅加载方案 Figure 7 Constant amplitude loading plan |
|
| 图 8 线性加载方案 Figure 8 Linear loading plan |
通过数值分析方法研究压电智能骨料在动荷载作用下工作性能的核心在于获得智能骨料内压电陶瓷片在动荷载作用下的输出电压,从而建立动荷载与输出电压之间的关系.压电陶瓷在受外力作用过程中会产生电压,该电压是压电陶瓷极化方向的上下等势面之间的电压差值.为获取该电压值,将压电陶瓷的下表面定义为零势面,从压电陶瓷上表面所得的电压值即为压电陶瓷受力过程中产生的电压值.在数值模拟中使用命令流进行处理,即使用*Equation命令,同时在施加动荷载作用时,将压电陶瓷片的底面设置为零势面,从而在计算结果中可以直接读取动荷载作用时压电陶瓷片的电压.
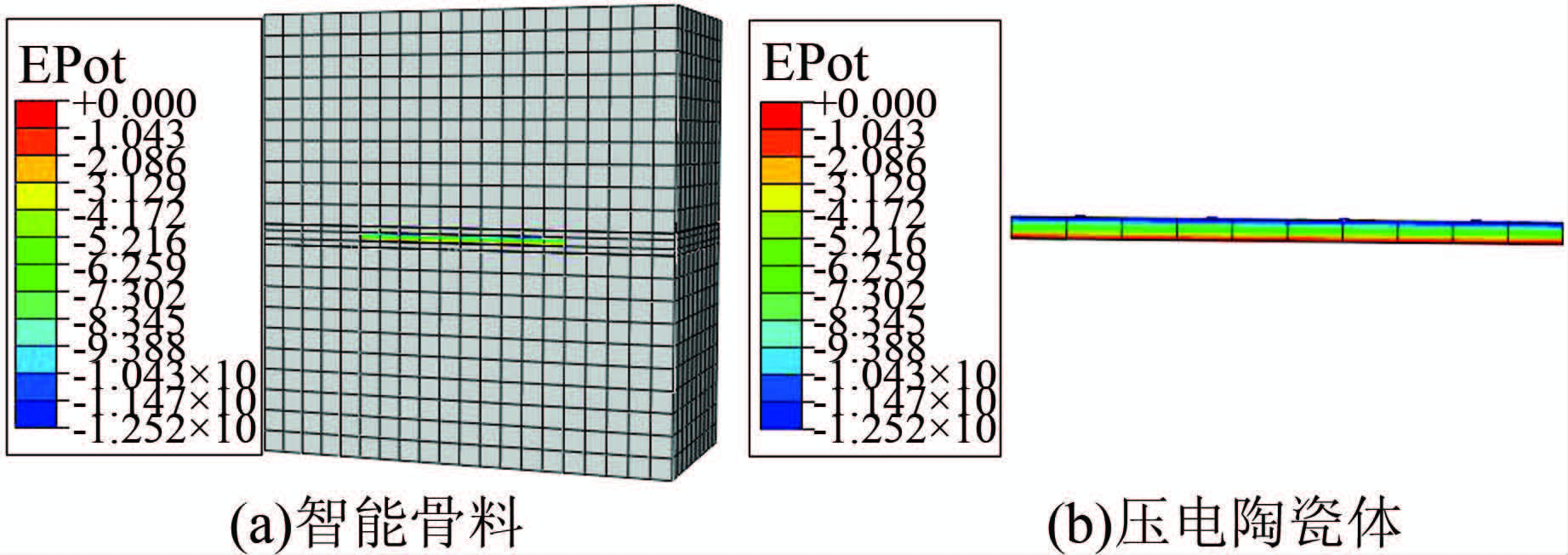
2.4 有限元模拟结果在数值模拟中对2种加载方案分别提交作业,图 9(a)为采取等幅加载方案时智能骨料的电势云图,图 9(b)为采取等幅加载方案时智能骨料中压电陶瓷片输出的电势云图,图 10(a)为采取线性加载方案时智能骨料的电势云图,图 10(b)为采取线性加载方案时智能骨料中压电陶瓷片输出的电势云图.从4个图可以看出:1)在动荷载作用下,无论是线性加载还是等幅加载,智能骨料中除了压电片具有压电性外,其余材料均不具备压电性,即只有压电陶瓷片发生电压变化,其余材料的电势始终为零;2)由于使用了*Equation 命令,而且在定义载荷时将压电陶瓷片底面设置为零势面,在等幅加载和线性加载时压电陶瓷片的输出电势云图中,压电陶瓷片内部电势出现分层现象,说明在动荷载作用下,在压电陶瓷片内部形成匀强电场,底面为零势面,顶面为最大电势面,其内部电压即为上下两面的电势差.
|
| 图 9 等幅加载电势云图 Figure 9 Nephogram of constant amplitude loading electric potential |
|
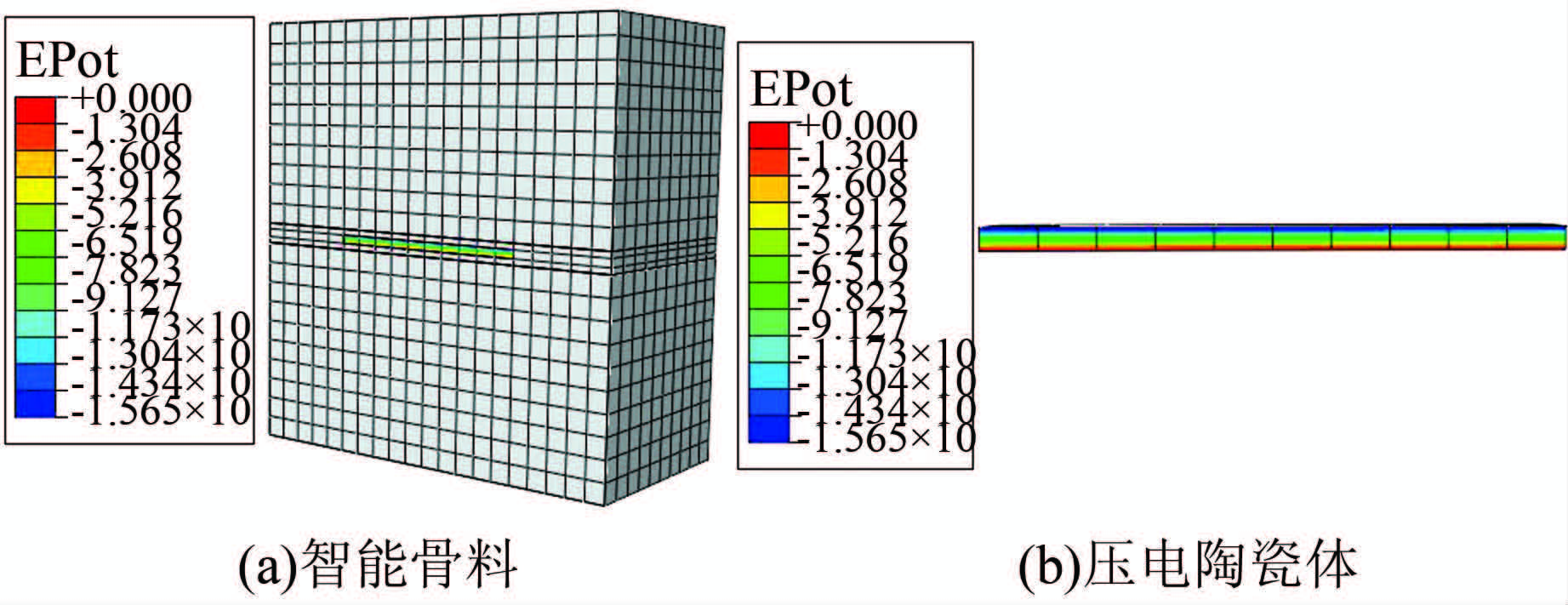
| 图 10 线性加载电势云图 Figure 10 Nephogram of linear load potentials |
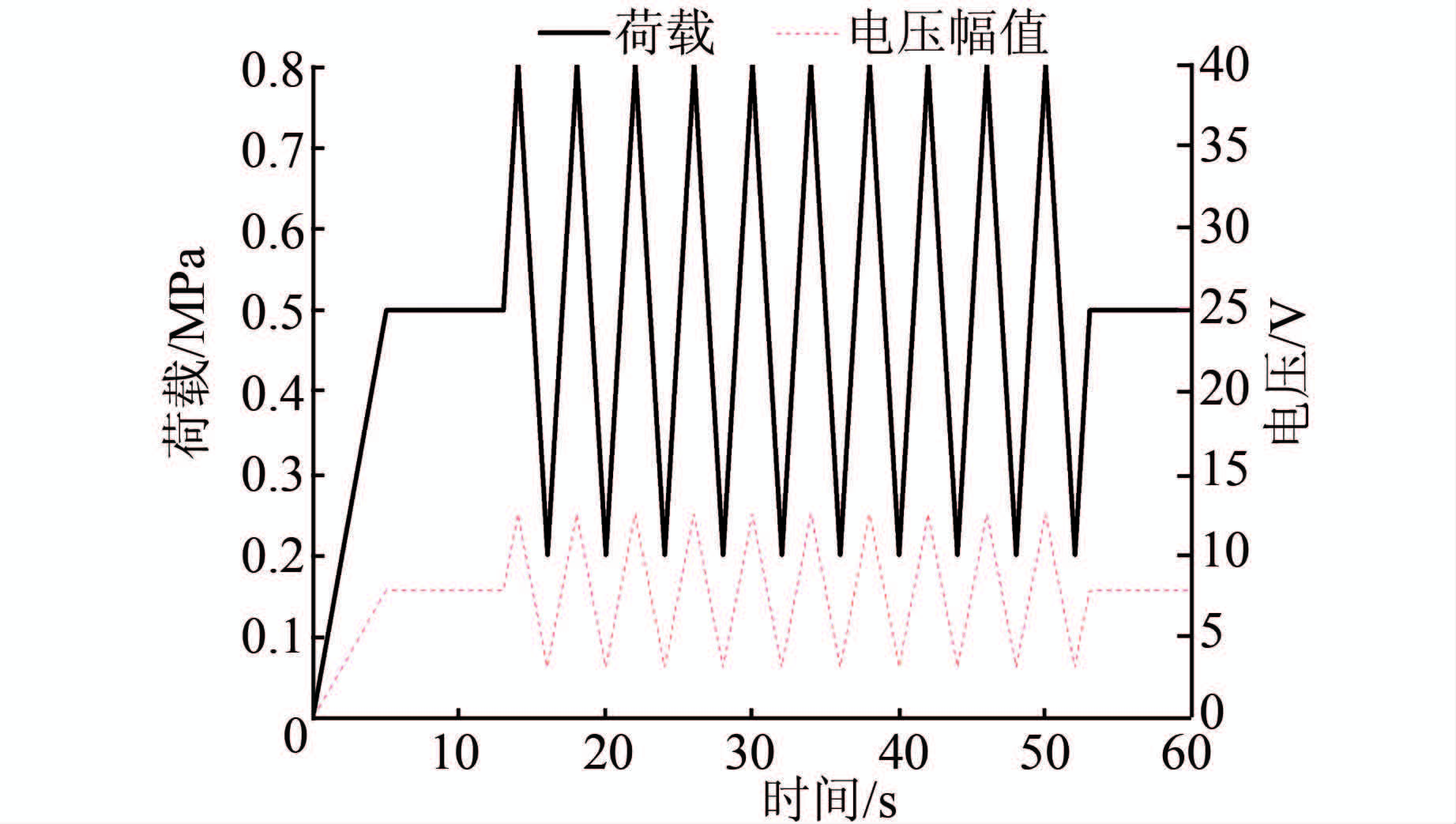
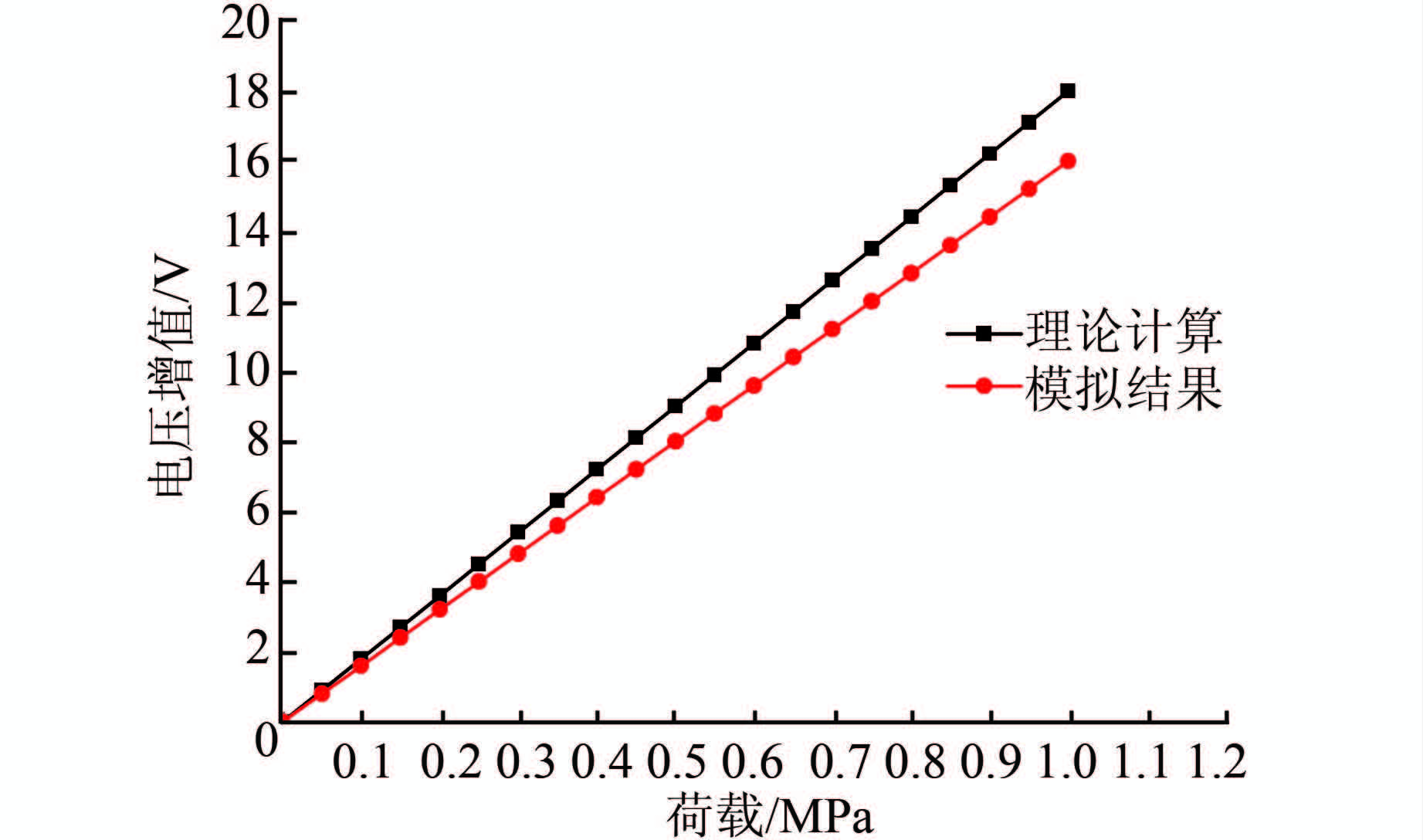
根据数值模拟计算结果,对计算数据进行整理分析,并绘制相关图形.图 11为采取等幅加载时荷载、电压与时间的关系曲线.由图 11可以看出,压电陶瓷片受到动荷载作用时的电压幅值与外荷载同频变化,并未出现滞延现象.图 12为采取线性加载时电压幅值与荷载的关系曲线,以及理论计算结果的曲线.由图 12可以看出,数值模拟结果中电压幅值与外荷载的线性关系良好.利用式(7)和有限元模拟结果计算得到的灵敏度S=1.6×10-5V/Pa,有限元模拟值与理论值最大相差为11%,表明本文建立的压电智能骨料有限元模型及所取得压电参数基本合理.
|
| 图 11 电压幅值变化的时间历程曲线 Figure 11 Time history curve of voltage amplitude changes |
|
| 图 12 电压幅值与动荷载关系图 Figure 12 Relationships between voltage amplitude and dynamic load |
为了解智能骨料在动力荷载作用下的工作机理和性能,进行了理论分析和数值模拟计算.
1) 智能骨料在受到外部动荷载作用时,封装在其内部的压电陶瓷片由于自身的压电效应而产生电荷移动,在压电陶瓷片的极化方向上形成电压,且电压幅值与动力荷载响应同步,没有滞延现象.
2) 通过理论分析与有限元模拟,验证了压电陶瓷片电压幅值与动荷载变化具有很好的线性关系,且数值模拟结果与理论分析结果一致性好,说明本文建立的有限元模型基本合理.
| [1] |
赵晓燕.基于压电陶瓷的结构健康监测与损伤诊断[D].大连:大连理工大学,2008.
Zhao Xiaoyan.Structural health monitoring and damage detection based on piezoelectric ceramic transducers[D].Dalian: Dalian University of Technology,2008. |
| [2] |
雷晋芳.基于压电智能路面的车辆动态称重技术的研究[D].大连:大连理工大学,2013.
Lei Jinfang.Vehicle weigh-in-motion technology research based on piezoelectric smart pavement[D].Dalian: Dalian University of Technology,2013. |
| [3] |
张海滨.基于压电智能骨料的钢筋混凝土结构地震应力检测方法[D].大连:大连理工大学,2012.
Zhan Haibing.Seismic stress monitoring for RC structures based on piezoelectric smart aggregates[D]. Dalian:Dalian University of Technology,2012. |
| [4] | Song G, Gu H, Mo Y L, et al. Health monitoring of a concrete structure using piezoceramic materials[J]. Smart Materials and Structures, 2005, 16(4): 959–968. |
| [5] | Song G, Gu H, Mo Y. Smart aggregates: multi-functional sensors for concrete structures——a tutorial and a review[J]. Smart Materials and Structures, 2008, 17(3): 33001. DOI:10.1088/0964-1726/17/3/033001 |
| [6] | Li Z, Qin L, Huang S. Embedded piezo-transducer in concrete for property diagnosis[J]. Journal of Materials in Civil Engineering, 2009, 21(11): 643–647. DOI:10.1061/(ASCE)0899-1561(2009)21:11(643) |
| [7] | Yang Xiaoming, Li Zhongxian, Ding Yang, et al. Test on sensor effect of cement matrix piezoelectric composite[J]. Transactions of Tianjin University, 2005(2): 133–136. |
| [8] |
侯爽, 雷晋芳, 欧进萍. 基于压电智能骨料的沥青混凝土路面车辆动态荷载监测[J].
振动与冲击, 2014, 33(4): 42–47.
Hou Shuang, Lei Jinfang, Ou Jinping. Vehicle load monitoring for asphalt concrete pavement based on smart aggregates[J]. Journal of Vibration and Shock, 2014, 33(4): 42–47. |
| [9] |
闵海涛, 史文库, 隋华. 压电悬置及对发电机振动主动控制的仿真分析[J].
汽车工程, 2014, 26(6): 671–675.
Min Haitao, Shi Wenku, Sui Hua. Piezoelectric mount and simulation analysis of active control for engine vibration[J]. Automotive Engineering, 2014, 26(6): 671–675. |
| [10] |
范兴明, 马世伟, 张鑫, 等. 基于ANSYS的压电陶瓷晶片PZT仿真分析[J].
压电与声光, 2014, 36(3): 416–420.
Fan Xinmin, Ma Shiwei, Zhang Xin, et al. Simulation analysis of piezoelectric ceramic chip PZT based on ANSYS[J]. Piezoelectrics and Acoustooptics, 2014, 36(3): 416–420. |
| [11] |
梁磊, 王少萍, 曹锋. 基于ANSYS的压电陶瓷PLZT特性仿真分析[J].
北京航空航天大学学报, 2008, 34(7): 853–856.
Liang Lei, Wang Shaoping, Cao Feng. Analysis of piezoelectric ceramics PLZT based on ANSYS[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(7): 853–856. |
| [12] |
马尧. 基于ABAQUS的压电悬臂梁有限元仿真分析[J].
吉林化工学院学报, 2014, 31(7): 49–52.
Ma Yao. Finite element emulation analysis of piezoelectric cantilever beam based on ABAQUS[J]. Journal of Jilin Institute of Chemical Technology, 2014, 31(7): 49–52. |
| [13] |
罗平. 基于ANSYS模态分析的压电陶瓷参数数据的转换及其输入[J].
广西技术师范学院学报(自然科学), 2009(3): 11–15.
Luo Ping. Modal analysis of piezoelectric parameter data conversion and input based on ANSYS[J]. Journal of Guangdong Polytechnic Normal University, 2009(3): 11–15. |
 2016, Vol. 49
2016, Vol. 49



