文章信息
- 李奔, 张坤, 程天矫
- LI Ben, ZHANG Kun, CHENG Tianjiao
- 基于层次分析法的澜沧江湄公河可消耗水量分配
- Application of AHP to Lancang RiverMekong River consumable water distribution
- 武汉大学学报(工学版), 2018, 51(5): 389-393
- Engineering Journal of Wuhan University, 2018, 51(5): 389-393
- http://dx.doi.org/10.14188/j.1671-8844.2018-05-003
-
文章历史
- 收稿日期: 2017-09-21
2. 武汉大学国家领土主权与海洋权益协同创新中心,湖北 武汉 430072;
3. 贵州省水利水电勘测设计院湖北分院,湖北 武汉 430070;
4. 湖北水利水电职业技术学院,湖北 武汉 430070
2. Center for Collaborative Innovation on Territorial Sovereignty and Marine Rights, Wuhan University, Wuhan 430072, China;
3. Hubei Branch of Guizhou Water Conservancy and Hydropower Survey and Design Institute, Wuhan 430070, China;
4. Hubei Water Resources Technical College, Wuhan 430070, China
国际河流水资源因自然越境而打破了流域各国领土的完整性,使其成为多国共享资源[1].随着经济社会的快速发展,国际河流水资源的分配将会变得更加紧迫[2].国际河流水资源冲突会直接影响河流自身的可持续发展以及流域各国之间的关系稳定,而实现公平合理的水资源分配是解决此类冲突的关键.Aaron[3]对国际河流水资源冲突的诱因进行了系统分析,并提出了关于用水量的分配方案;何大明[4]、陈海燕[5]等先后研究了国际河流水资源分配的特点、模式、原则、指标体系和影响;Bhagabati[6]利用博弈理论提出了解决复杂条件下的跨界水分配问题的新方法;Pech等[7]对湄公河流域的水分配提出了新的设计框架;Mirja等[8]分析了源出中国的6条国际河流的水资源问题,其中提到水资源的合理分配是影响区域稳定的重要因素.层次分析方法既有定性分析又有定量计算,针对国际河流水量分配问题的系统复杂性与目标多样性,比其他方法具有更好的操作性与可靠性.符传君[9]对层次分析法进行了改进,并用于海南省水资源配置评价指标计算,计算结果较满意;游进军等[10]利用层次分析法改进了水资源配置方案评价的指标体系,并通过实例计算方案验证了改进方法的适用性;Bojan等[11]基于层次分析法建立了San Francisco河的水资源管理决策模型,并对Paraguacu流域的水资源决策进行了有效评估.本文针对各国存在的问题、需水情况,主要应用层次分析法进行水量分配研究,并以澜沧江-湄公河为应用案例,得出相应的水量分配结果,争取最优化解决问题,避免因分配不合理引起国家之间的冲突.
1 流域概况澜沧江-湄公河流域丰富的水资源是推动区域社会经济发展的重要因素,同时也是限制区域社会经济发展的关键制约因子.流域各国之间正在积极寻求合作开发利用流域水资源,优化水资源的分配.澜沧江-湄公河贯穿中国、老挝、缅甸、泰国、柬埔寨、越南6国,流域面积81万km2,全长4 880 km,流域位置及其水资源概况见图 1与表 1.流域总水量丰富,多年平均径流量4 750亿m3,但径流的时空分布有较大的差异;流域内的水量消耗主要是灌溉用水,集中于下游各国;近年来伴随着流经地区人口的日益增多,工农业生产规模也逐渐增大,如何对流域水资源进行合理分配,是解决各国之间的需水矛盾、提高流域水资源利用效率所面临的重要问题.
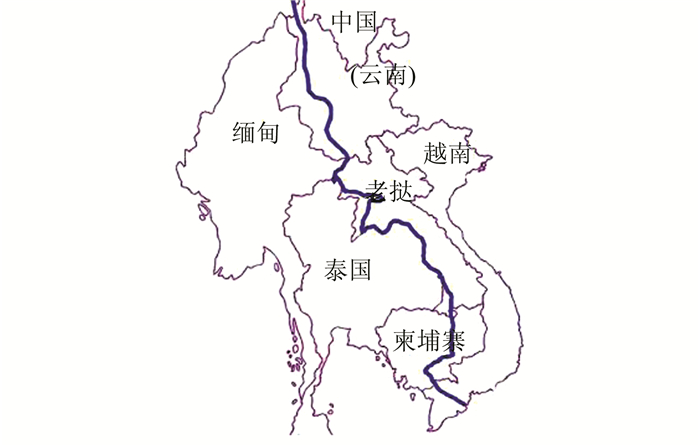
|
| 图 1 澜沧江-湄公河流域位置 Figure 1 Geographical position of Lancang River-Mekong River basin |
| 国家 | 流经里程/km | 流域面积/(万km2) | 产水量/(亿m3) | 产水量所占比例/% | 水资源分布/(亿m3) | 水电蕴藏量/(万kW) |
| 中国 | 2 161.1 | 16.7 | 2 410 | 16.0 | 765 | 3 656.4 |
| 缅甸 | 265.0 | 2.1 | 300 | 2 | 95 | 5国合计:5 800.0 |
| 老挝 | 1 987.7 | 21.4 | 5 270 | 35 | 1 662.5 | |
| 泰国 | 976.3 | 18.2 | 2 560 | 17 | 850 | |
| 柬埔寨 | 501.7 | 16.1 | 2 860 | 19 | 855 | |
| 越南 | 229.8 | 6.5 | 1 660 | 11 | 522.5 | |
| 合计 | 4 880.0 | 81.0 | 15 060 | 100 | 4 750 | 9 456.4 |
| 注:澜沧江-湄公河流经各自里程含界河在内,有重复计算. | ||||||
研究拟采用层次分析方法对澜沧江-湄公河水量分配进行计算研究.作为一种经典的决策方法,层次分析法最初是由美国学者Saaty[12]提出的,该方法主要帮助决策人将复杂的决策系统层次化,逐层分析和计算各个决策影响因素的重要性,为最后的决策提供依据.
2.1 建立层次结构模型将复杂问题分解为多个组成元素,根据元素之间的隶属关系划分为不同的层次,最高层次也就是解决该复杂问题的总目标,层次数与问题的复杂程度和分析的需求程度有关.
2.2 构建判断矩阵根据n个元素,可以给出两两相互比较的判断矩阵Cu=(Cij)n×n,其中Cij代表元素i和元素j对目标的重要性程度.该矩阵Cu的含义如下:
1) Cij>0;
2) Cij=1/Cji (i、j不相等);
3) Cii=1.
2.3 层次单排序及其一致性检验在求出判断矩阵Cu的最大特征根λmax及对应的特征向量W=c1, c2, …, cn后,将之归一化,得到同一层次上相应因素对于上一层次某因素重要性的排序权值,然后对其进行一致性检验.
1) 计算一致性指标CI=λmax-n/n-1;
2) 查询同阶的平均随机一致性指标RI;
3) 求得随机一致性比例CR:
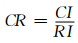 (1)
(1)
CR < 0.1时,表示判断矩阵达到一致性检验的要求,否则需要适当修改矩阵的标度大小.
2.4 层次总排序及其一致性检验最后计算同一层次所有因素对最高层次某因素相对重要性的排序权值,应用总排序的随机一致性比率进行一致性检验,利用各层的权重排序,可以从上至下得出最低层相对于最高层的权重排序.
3 层次分析法在澜沧江-湄公河水量分配中的应用将澜沧江-湄公河流域内各个国家作为计算单位,以公平性、效率性与可持续性作为流域层面水量分配的3个基本指导准则,选取相对应的影响分水的各个指标,构建层次结构逻辑图,计算求得流域各国的分水权重与水量.
3.1 选取分水指标基于概念清楚、计算方便与各自独立的需要,分别从水量分配的公平性、效率性和可持续性出发选取相应的指标.
1) 公平性
按照公平准则,可选取流域国家的工业用水量(C1)、农业用水量(C2)、生活用水量(C3)、人口总数(C4)、GDP总量(C5)、人均需水量(C6)共6个指标.
2) 效率性
根据效率准则,可选取流域国家的单方水工业产值(C7)、人均GDP(C8)、单方水GDP(C9) 3个指标.
3) 可持续性
根据可持续性准则,可选取流域国家的人口自然增长率(C10)与流域森林覆盖率(C11)2个指标.
3.2 构造各层次判断矩阵和层次指标权重计算根据各影响指标绘制层次结构图, 见图 2.
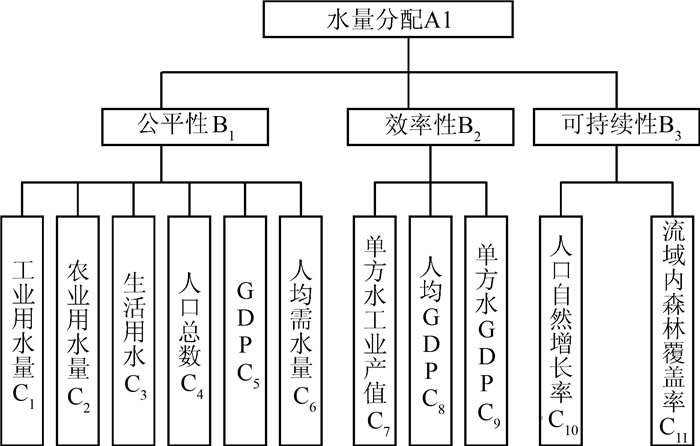
|
| 图 2 层次结构图 Figure 2 Hierarchical structure model |
从图 2中的第2层开始,将从属于上一层各个因素的同一层对应的因素,采取成对比较方法和1~9数字标度方法,具体的赋值方法见表 2所示,构建成对比较矩阵.然后,对其进行层次单排序以及一致性检验.如果通过了一致性检验,特征向量即是权向量;如果没有通过,就需要构建新的成对比较矩阵.最终计算得出各指标层次的总权重和总排序.根据同一层次中所有单排序的结果,按照层次高低逐一计算全部指标的层次总权重和总排序,计算结果见表 3.
| A与B比较的语义描述 | A等于B | A稍强于B | A强于B | A很强于B | A绝对强于B |
| A与B比较对应的量化值 | 1 | 3 | 5 | 7 | 9 |
| 目标层 | 目标层权重 | 准则层 | 准则层权重 | 指标层 | 指标层对应的准则层权重 | 指标总权重 | 指标层次总排序 |
| 水量分配A | 1 | 公平性B1 | 0.2 | 工业用水量C1 | 0.161 9 | 0.032 4 | 8 |
| 农业用水量C2 | 0.128 5 | 0.025 7 | 11 | ||||
| 生活用水量C3 | 0.128 5 | 0.025 7 | 10 | ||||
| 人口总数C4 | 0.161 9 | 0.032 4 | 6 | ||||
| GDP C5 | 0.257 1 | 0.051 4 | 4 | ||||
| 人均需水量C6 | 0.161 9 | 0.032 4 | 5 | ||||
| 效率性B2 | 0.3 | 单方水工业产值C7 | 0.106 6 | 0.031 1 | 7 | ||
| 人均GDP C8 | 0.318 3 | 0.095 5 | 9 | ||||
| 单方水GDP C9 | 0.575 0 | 0.172 5 | 2 | ||||
| 可持续性B3 | 0.5 | 人口自然增长率C10 | 0.200 0 | 0.100 0 | 3 | ||
| 森林覆盖率C11 | 0.800 0 | 0.400 0 | 1 |
结合澜沧江-湄公河流域国家的数据资料,计算各个国家的所有指标评价值,其方法与综合权重法相同.把流域各国所有指标评价值的结果构建成评价值矩阵R(rmn),然后将其与指标权重向量W(wn)相乘,可以得出各个国家的分水权重G(gm),如表 4所示;最后把分水权重与总水量相乘,即可得到分配水量.
| 指标 | 中国D1 | 老挝D2 | 缅甸D3 | 泰国D4 | 柬埔寨D5 | 越南D6 | 合计 |
| 工业用水量C1 | 0.003 2 | 0.003 3 | 0.001 6 | 0.016 2 | 0.001 6 | 0.006 3 | 0.032 2 |
| 农业用水量C2 | 0.005 3 | 0.002 7 | 0.001 9 | 0.010 7 | 0.001 3 | 0.003 8 | 0.025 7 |
| 生活用水量C3 | 0.005 2 | 0.002 6 | 0.001 9 | 0.010 5 | 0.001 8 | 0.003 7 | 0.025 7 |
| 人口总数C4 | 0.003 0 | 0.001 5 | 0.005 7 | 0.008 9 | 0.002 7 | 0.010 6 | 0.032 4 |
| GDP C5 | 0.008 7 | 0.003 0 | 0.002 9 | 0.007 7 | 0.016 6 | 0.012 3 | 0.051 2 |
| 人均需水量C6 | 0.006 2 | 0.002 0 | 0.003 6 | 0.002 2 | 0.014 9 | 0.003 4 | 0.032 3 |
| 单方水工业产值C7 | 0.004 3 | 0.003 8 | 0.001 7 | 0.016 8 | 0.001 9 | 0.004 1 | 0.032 6 |
| 人均GDP C8 | 0.018 5 | 0.005 8 | 0.010 5 | 0.006 5 | 0.044 1 | 0.010 2 | 0.095 6 |
| 单方水GDP C9 | 0.028 1 | 0.014 1 | 0.011 7 | 0.081 1 | 0.014 1 | 0.023 4 | 0.172 5 |
| 人口自然增长率C10 | 0.007 9 | 0.022 3 | 0.020 9 | 0.009 7 | 0.020 9 | 0.018 2 | 0.099 9 |
| 森林覆盖率C11 | 0.044 8 | 0.047 1 | 0.047 1 | 0.089 7 | 0.081 5 | 0.089 7 | 0.399 9 |
| 合计 | 0.135 2 | 0.108 2 | 0.109 5 | 0.260 0 | 0.201 4 | 0.185 7 | 1.000 0 |
由表 4可见中国、老挝、缅甸、泰国、柬埔寨、越南6个流域国家综合分配的水量权重依次为13.52%、10.82%、10.95%、26.00%、20.14%、18.57%.
3.4 水量分配结果将分水权重与规划水平年的分水总量相乘,即可得到各个国家的分配水量.澜沧江-湄公河多年平均径流量为764.8亿m3,根据该流域各国的用水现状及未来的用水需求,采用的分配总水量按多年平均径流量的10%计算,即为76.48亿m3,各国的分配水量结果可见图 3.
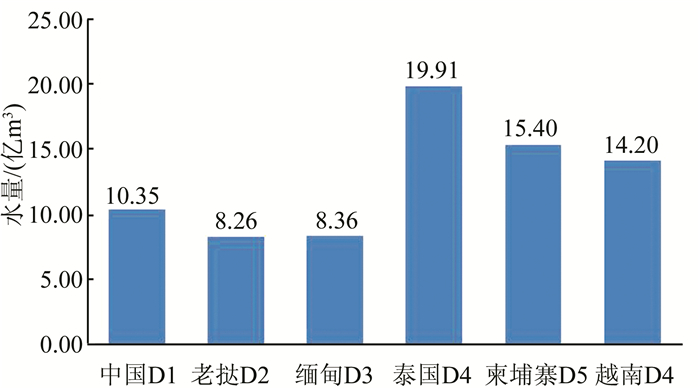
|
| 图 3 各国水量分配结果 Figure 3 Water distribution results of basin countries |
澜沧江-湄公河流经6个国家,每个国家的政治、社会、经济、地理等都有较大的区别,这种差异对水量分配具有很大程度的影响.从表 4并结合图 3可知,在公平性、效率性、可持续性3大准则的框架下,可持续性准则所占比重明显较大,在纵向对比过程中,人口自然增长率C10与流域森林覆盖率C11占据的相应分配水量较大.每个国家的国情不同,对水量分配的影响存在很大差别.中国的GDP C5权重为0.008 7,分配水量较其他5项指标最大;老挝各项指标权重均匀,分配水量也相对平均;缅甸人口总数C4权重为0.005 7,分配水量较其他5项指标最大;泰国分配的水量最多,主要由于其人均GDP所占权重最大,且其农业用水量在横向比较中所占的比例也较大;柬埔寨的GDP C5、人均需水量C6两方面所占权重分别为0.016 6和0.014 9,这两项分配水量较多;越南的GDP C5所占权重为0.012 3,分配水量较多.
各个国家在效率性B2和可持续性B3所对应的5项指标中,国与国之间表现出的差异比较明显,通过表 4可以清晰地看出,尤其是指标C11表现最为明显,在此不做过多分析.相对其他的研究成果,该水量分配结果更加注重了流域各国的可持续发展诉求,更好地体现了跨境水资源合作与开发的最新发展趋势.
5 结论人口自然增长率和森林覆盖率对于水量分配比重贡献最大, 公平性和效率性对应的9项指标对于水量分配的影响相对较小,但也是影响水量分配的重要因素,其中人均GDP和国家总GDP比重相对较大,其他各因素对水量分配的影响不明显.澜沧江-湄公河水量分配是多方面作用的结果,本研究只是一种理论分析计算,与实际状况难免有出入.另外,由于条件限制,本研究未考虑因支流入汇、干流梯级水库调度等条件对径流造成的影响,将在今后的研究中补充和完善.
| [1] | Asit K Biswas. Management of international waters: opportunities and constraints[J]. International Journal of Water Resources Development, 1999, 15(4): 429–441. DOI:10.1080/07900629948691 |
| [2] |
陈丽晖, 何大明. 澜沧江-湄公河整体水分配[J].
经济地理, 2001, 21(1): 28–32.
Chen Lihui, He Daming. The whole water allocation of the Lancang-Mekong River[J]. Economic Geography, 2001, 21(1): 28–32. |
| [3] | Aaron T Wolf. Criteria for equitable allocations: The heart of international water conflict[J]. Natural Resources Forum, 1999, 23(1): 3–30. DOI:10.1111/narf.1999.23.issue-1 |
| [4] |
何大明, 汤奇成.
中国国际河流[M]. 北京: 科学出版社, 2000.
He Daming, Tang Qicheng. China International River[M]. Beijing: Science Press, 2000. |
| [5] |
陈海燕. 可利用水量变化影响国际河流分水的实例及其启示[J].
水利发展研究, 2006(7): 53–56.
Chen Haiyan. Example of available water changes affecting international river water allocation and its enlightenment[J]. Water Resources Development Research, 2006(7): 53–56. |
| [6] | Seemant Bhagabati, Akiyuki Kawasaki, Mukand Babel, et al. A cooperative game analysis of transboundary hydropower development in the lower Mekong: case of the 3S sub-basins[J]. Water Resources Management, 2014, 28: 3417–3437. DOI:10.1007/s11269-014-0594-2 |
| [7] | Pech Sokhem, Kengo Sunada, Satoru Oishi. Managing transboundary rivers: The case of the Mekong River basin[J]. Water International, 2007, 32: 503–523. DOI:10.1080/02508060.2007.9709685 |
| [8] | Mirja Kattelus, Matti Kummu, Marko Keskinen, et al. China's southbound transboundary river basins: A case of asymmetry[J]. Water International, 2015, 40: 113–138. DOI:10.1080/02508060.2014.980029 |
| [9] |
符传君. 海南省水资源配置决策的层次分析模型研究[J].
中国水利水电科学研究院学报, 2007, 5(5): 212–217.
Fu Chuanjun. Level analysis model of water resources allocation decision-making in Hainan province[J]. Journal of China Institute of Water Resources and Hydropower Research, 2007, 5(5): 212–217. |
| [10] |
游进军, 赵帆, 杨聪, 等. 针对水资源配置评价的定量指标改进层次分析法研究[J].
水利水电技术, 2010, 41(3): 6–9.
You Jinjun, Zhao Fan, Yang Cong, et al. An improved analytic hierarchy process (AHP) for the quantitative evaluation of water resources allocation[J]. Water Resources and Hydropower Engineering, 2010, 41(3): 6–9. |
| [11] | Bojan Srdjevic. Linking analytic hierarchy process and social choice methods to support group decision-making in water management[J]. Decision Support Systems, 2007, 42: 2261–2273. DOI:10.1016/j.dss.2006.08.001 |
| [12] | Saaty T L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation[M]. McGraw-Hill: 1980. |
 2018, Vol. 51
2018, Vol. 51



