武汉大学学报(工学版)   2016, Vol. 49 Issue (4): 616-620

文章信息

张淑娥, 刘洋, 梁芷睿, 李骁睿, 安茜雯
ZHANG Shue, LIU Yang, LIANG Zhirui, LI Xiaorui, AN Qianwen
降低辐射功率的圆柱谐振腔缝隙优化模型
Optimization model of reducing radiation power of cylindrical resonant cavity gap
武汉大学学报(工学版), 2016, 49(4): 616-620
Engineering Journal of Wuhan University, 2016, 49(4): 616-620
http://dx.doi.org/10.14188/j.1671-8844.2016-04-022

文章历史

收稿日期: 2015-10-12
 Abstract              PDF               Figures               Tables
引用本文 0
张淑娥, 刘洋, 梁芷睿, 李骁睿, 安茜雯. 降低辐射功率的圆柱谐振腔缝隙优化模型[J]. 武汉大学学报(工学版), 2016, 49(4): 616-620.
ZHANG Shue, LIU Yang, LIANG Zhirui, LI Xiaorui, AN Qianwen. Optimization model of reducing radiation power of cylindrical resonant cavity gap[J]. Engineering Journal of Wuhan University, 2016, 49(4): 616-620.
降低辐射功率的圆柱谐振腔缝隙优化模型
张淑娥1, 刘洋2, 梁芷睿1, 李骁睿1, 安茜雯1     
1. 华北电力大学电气与电子工程学院，河北 保定 071003;
 2. 华北电力大学能源动力与机械工程学院，河北 保定 071003
收稿日期: 2015-10-12
作者简介: 张淑娥(1964-)，女，副教授，硕士生导师，研究方向为微波传感与技术，E-mail:zhang_shu_e@sina.com.
基金项目: 河北省自然科学基金资助项目(编号：E2013502298).
摘要: 研究圆柱谐振腔圆环缝隙的优化设计方法，首先说明了微波谐振腔微扰法原理以及辐射功率对腔体工作的影响；然后，利用HFSS进行了辐射功率的仿真计算，为便于将结果用于优化设计中，用类二次高斯函数对辐射功率数据进行拟合，得到其关于开缝宽度和开缝位置的二元拟合关系式；最后，建立了以辐射功率最小为目标函数的优化模型，并利用HFSS进行了数值仿真，验证了方法的可行性.结果表明，利用该方法能够减少圆柱谐振腔的辐射量，为谐振腔体缝隙的优化设计提供了一种新的思路.
关键词： 圆柱谐振腔     缝隙辐射功率     HFSS仿真     高斯函数拟合     线性约束优化模型    
Optimization model of reducing radiation power of cylindrical resonant cavity gap
ZHANG Shue1, LIU Yang2, LIANG Zhirui1, LI Xiaorui1, AN Qianwen1     
1. School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China;
 2. School of Energy, Power & Mechanical Engineering, North China Electric Power University, Baoding 071003, China
Abstract: This paper mainly studies the optimization design method of annular gap in the cylindrical resonant cavity. Firstly, we illustrate the microwave resonant cavity perturbation method and gap radiation power’s influence on the cavity; and then using HFSS to simulate the radiation power calculation. In order to apply the facilitate results to optimal design conveniently, quadratic Gaussian function is used to fit the data of the radiation power to get fitting equation between the gap width and position. Finally, we establish optimization model for the purpose of minimum radiation power based on the fitting function and use HFSS numerical simulation to verify the feasibility of the method. The results show that this method can reduce the radiation of the cylindrical cavity, so as to provide a new idea for the optimization design of the gap on the resonant cavity.
Key words: cylindrical resonant cavity     gap radiation power     HFSS simulation     Gaussian function fitting     linear constraint optimization model    

蒸汽两相凝结流动广泛存在于自然界和工程领域.常规火力发电厂中大型凝汽式汽轮机的末几级和核电站中汽轮机的全部级都在湿蒸汽状态下工作，蒸汽湿度的大小直接影响汽轮机运行的安全性和经济性[1-5].蒸汽湿度增加，一方面会对汽轮机叶片产生强烈的腐蚀和冲击，使叶片变得粗糙，出现凹坑，甚至造成叶片扭曲断裂，严重威胁汽轮机的安全运行，另一方面也降低了汽轮机的热效率[4-9].因此，蒸汽湿度的准确测量对工业生产及指导电厂汽轮机安全经济运行具有重要意义[1].

蒸汽湿度的测量方法主要包括热力学法、光学法、微波谐振腔微扰法、失踪与导电法、分离法、临界速度法及利用孔板测量等[10-15].文章主要针对微波谐振腔微扰法.该方法测量湿度所用的传感器为一个开有圆环缝隙的圆柱形微波谐振腔，其圆环缝隙的设计需要综合考虑几个方面的因素.首先，为准确捕捉谐振腔微扰时谐振频率的变化，需要保证水蒸气气流畅通，所以缝隙尺寸不能过小.但是，腔体内电磁场会穿过圆环缝隙产生辐射，这会导致输入测量功率的损失，并且会产生干扰模式，降低品质因数等，所以缝隙尺寸不能过大.综上，优化谐振腔圆环缝隙的设计具有重要的实际意义.

文章主要研究谐振腔圆环缝隙的优化设计方法，优化的首要原则是减小缝隙处的近场辐射量.首先利用HFSS仿真得到不同开缝情况下缝隙处的辐射量，再用高斯函数对数据进行拟合，得到辐射量关于开缝宽度和开缝位置的二元函数.建立并求解以辐射量最小为目标函数的优化模型，从而得到谐振腔圆环缝隙的优化设计方案.最后，利用HFSS进行仿真，验证方案的可行性.

1 微波谐振腔微扰法简介

微波谐振腔微扰法基本思想是基于微波谐振腔的微扰，即微波谐振腔的谐振频率随腔内电介质的介电常数变化将发生偏移，在一定温度(或压力)下，蒸汽的湿度不同其介电常数也不同，一定温度、压力下湿蒸汽的介电常数只与其湿度有关.因此，当湿蒸汽流过微波谐振腔时，通过测量谐振腔谐振频率的偏移，可以测量湿蒸汽的介电常数，进而确定蒸汽的湿度[9].

圆柱形微波谐振腔构造简单，加工制造方便，品质因数高，应用广泛，因此，选用圆柱形谐振腔作为蒸汽湿度的测量传感器.腔体两端有环形网栅，可使湿蒸汽在腔中自由流过.

谐振腔的工作模式选取TE011模式，它是TE型模中唯一没有简并的模式，场结构稳定，即使腔体有微小变形也对谐振频率影响不大，场分布稳定而不会发生模式分裂.图 1为圆柱形谐振腔模式的场结构图，实线为电力线，虚线为磁力线.TE011模的电场只有圆周方向的分量，磁场只有r方向和z方向的分量[7-10].

图 1 圆柱形谐振腔模式的场结构图 Figure 1 Field structure of cylindrical cavity mode
图选项

当介电常数为εr的湿蒸汽流过谐振腔时，谐振腔的谐振频率将发生偏移，使用谐振腔微扰理论分析其谐振频率的变化，可以得到谐振频率改变量Δf和介质的介电常数εr的关系为[2]

$\frac{\Delta f}{{{f}_{0}}}=-\frac{\left( {{\varepsilon }_{r}}-1 \right)}{2}$    (1)

其中f0为蒸汽通过前腔内的谐振频率：

${{f}_{0}}=\frac{1}{2\pi \sqrt{\mu \varepsilon }}\sqrt{{{\left( 3.832/a \right)}^{2}}+{{\left( \pi /l \right)}^{2}}}$    (2)

式中:l为谐振腔长度;R为谐振腔半径.

只要测量出谐振腔的谐振频率的改变量，由式(1)就可以得到蒸汽的介电常数，再由介电常数和湿度的对应关系即可得到蒸汽的湿度[14].

在谐振腔半封闭情况下，通过圆环缝隙的面壁电流会向外产生近场辐射，过大的辐射量会对人体产生影响；另外，辐射降低了谐振腔内的储存能量，会造成不必要的功率流失；辐射的电磁场还会产生对谐振腔主模的干扰模式，扰乱主模谐振，不利于扫频观察和捕捉.所以以降低缝隙处的电磁场辐射功率为原则，设计了圆柱谐振腔体缝隙的优化模型.

2 缝隙辐射功率的拟合关系式

由于圆柱谐振腔体辐射功率的计算需要考虑缝隙处的复杂边界条件，难以得到严格的解析表达式，而且需要数值积分、矩阵求解等复杂计算，难以用于优化模型当中.为此，利用HFSS电磁仿真对微波谐振腔的多种缝隙位置、宽度进行仿真，得到大量数据，再利用数据得到辐射功率和开缝位置、宽度的拟合关系式，为下一步的优化模型求解做准备.HFSS电磁仿真的圆柱谐振腔如图 2所示.

图 2 HFSS下的圆柱谐振腔 Figure 2 Cylindrical resonant cavity under HFSS
图选项
2.1 单个缝隙辐射功率的数值求解

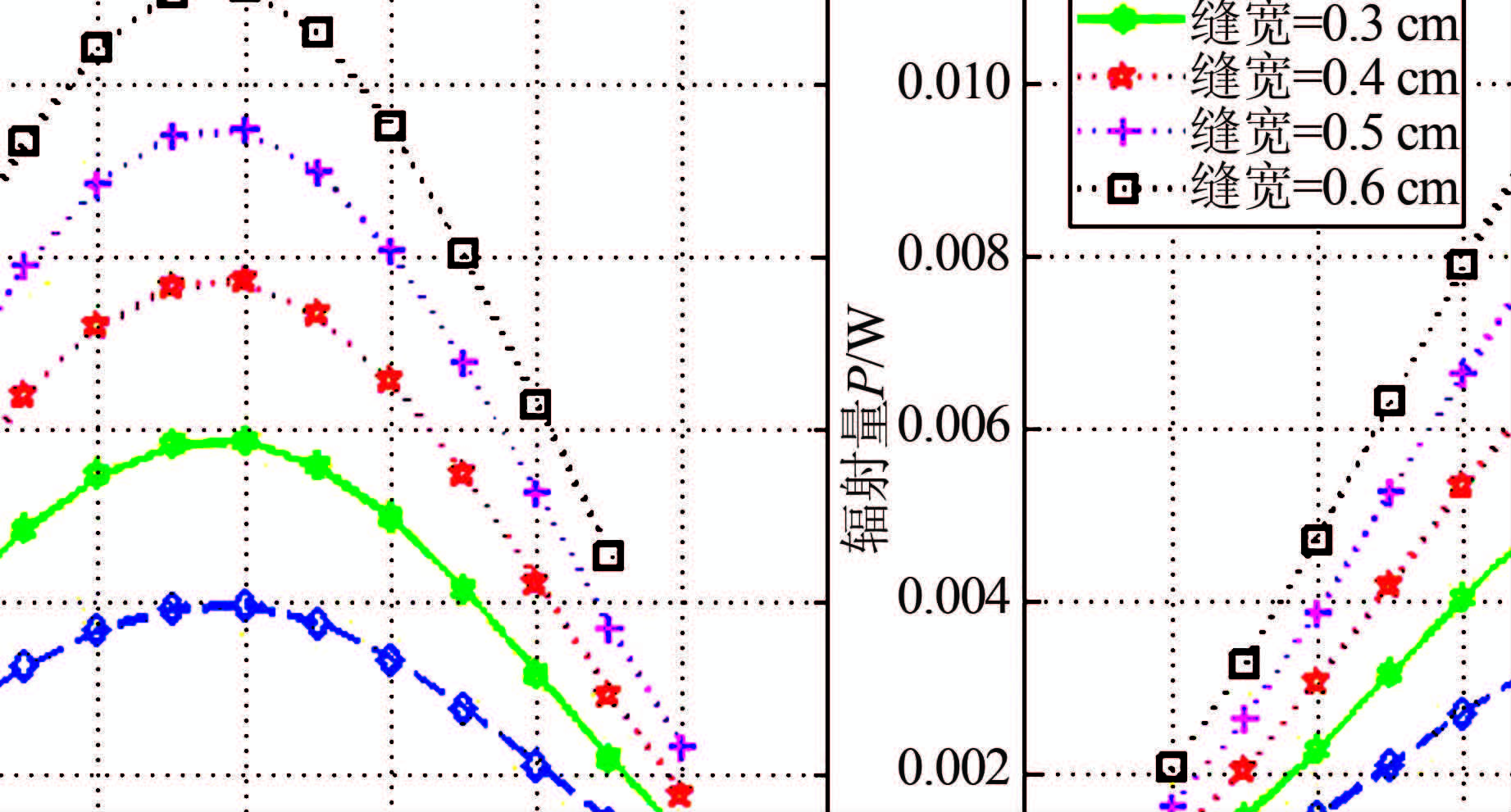
利用HFSS建立了某一尺寸的单缝腔体三维模型，设定好材料、边界、激励频率等条件进行数值求解，得到在某一半径R=2 cm的圆柱谐振腔上，开缝宽度为Δw=0.2~0.6 cm且处于不同位置时的辐射功率数值，计算结果如图 3所示.

图 3 不同位置和宽度下的圆柱谐振腔缝隙辐射功率 Figure 3 Radiated power of cylindrical cavity under different positions and widths
图选项

图 3中，横坐标r代表缝隙的中圆半径(为缝隙内外半径之和1/2圆的半径)，用来表示缝隙在腔体开缝平面上的位置.由图可知，缝隙的辐射量随着宽度的增加而增加，随着缝隙位置的外移先增加后减小.

2.2 辐射功率的拟合关系式及误差检验

由数值求解结果的图像可知，不同开缝位置下的辐射功率分布比较满足高斯函数的特征，开缝宽度影响的主要是高斯函数的参数.为此，利用MATLAB进行2次高斯函数拟合和高斯函数参数与开缝宽度的拟合，得到辐射功率的拟合关系式：

$\begin{align} & P=0.016\Delta w\times \exp \left( -{{\left( \frac{r-\left( 1.23+0.03\cos (16.24\Delta w)+0.05\sin (16.24\Delta w) \right)}{0.5044} \right)}^{2}} \right) \\ & +0.001\times (2+\cos (15.71\Delta w) \\ & +\sin (15.71\Delta w))\times \exp \left( -{{\left( \frac{r-\left( 0.76+0.08\cos (15.39\Delta w)+0.06\sin (15.39\Delta w) \right)}{0.3605} \right)}^{2}} \right) \\ \end{align}$    (3)

式中：P是缝隙的辐射功率;r是缝隙的中圆半径;Δw为开缝宽度.利用拟合关系式，将仿真数据转换成了辐射功率有关于开缝宽度和开缝位置的二元关系式P=f(r,Δw).

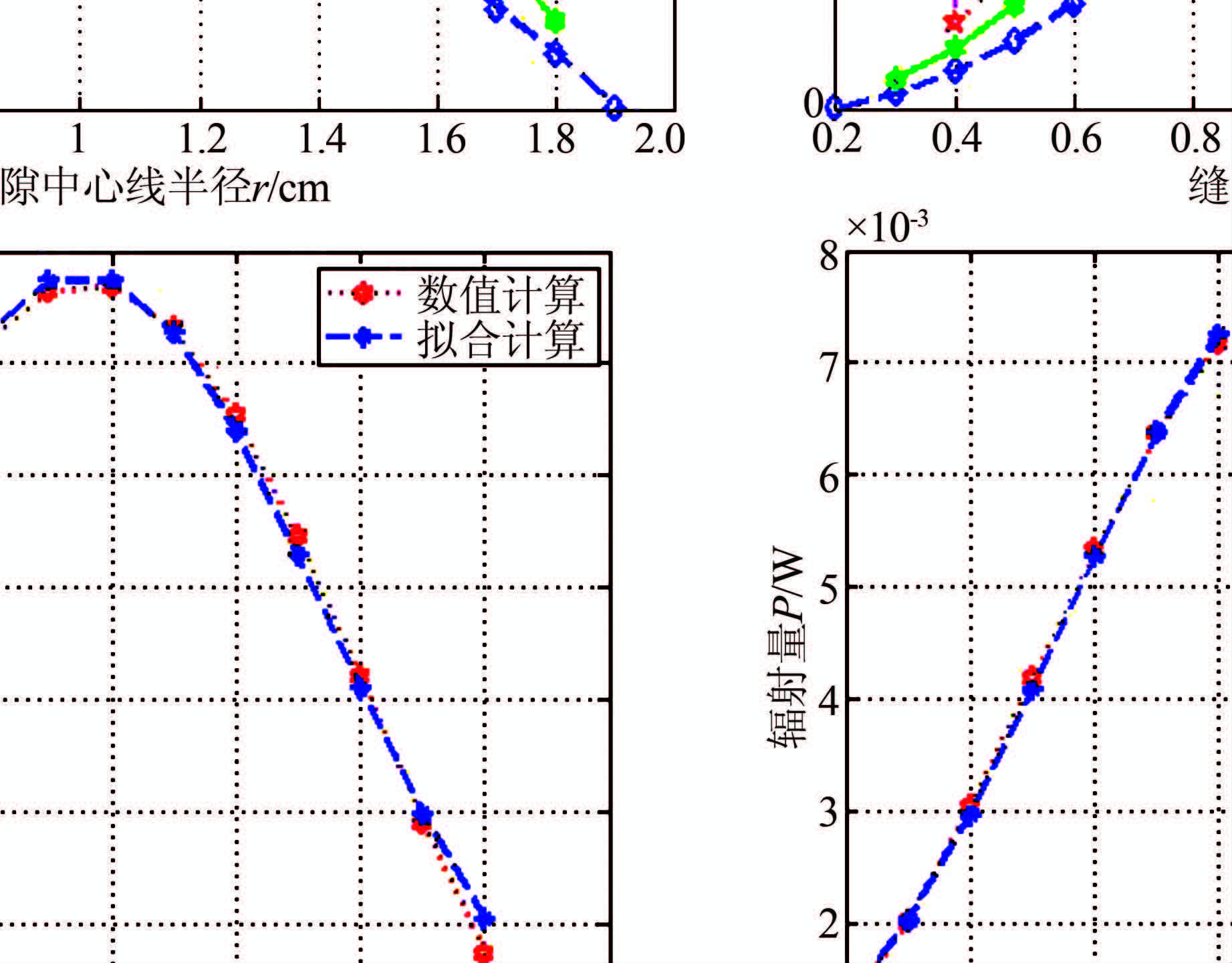
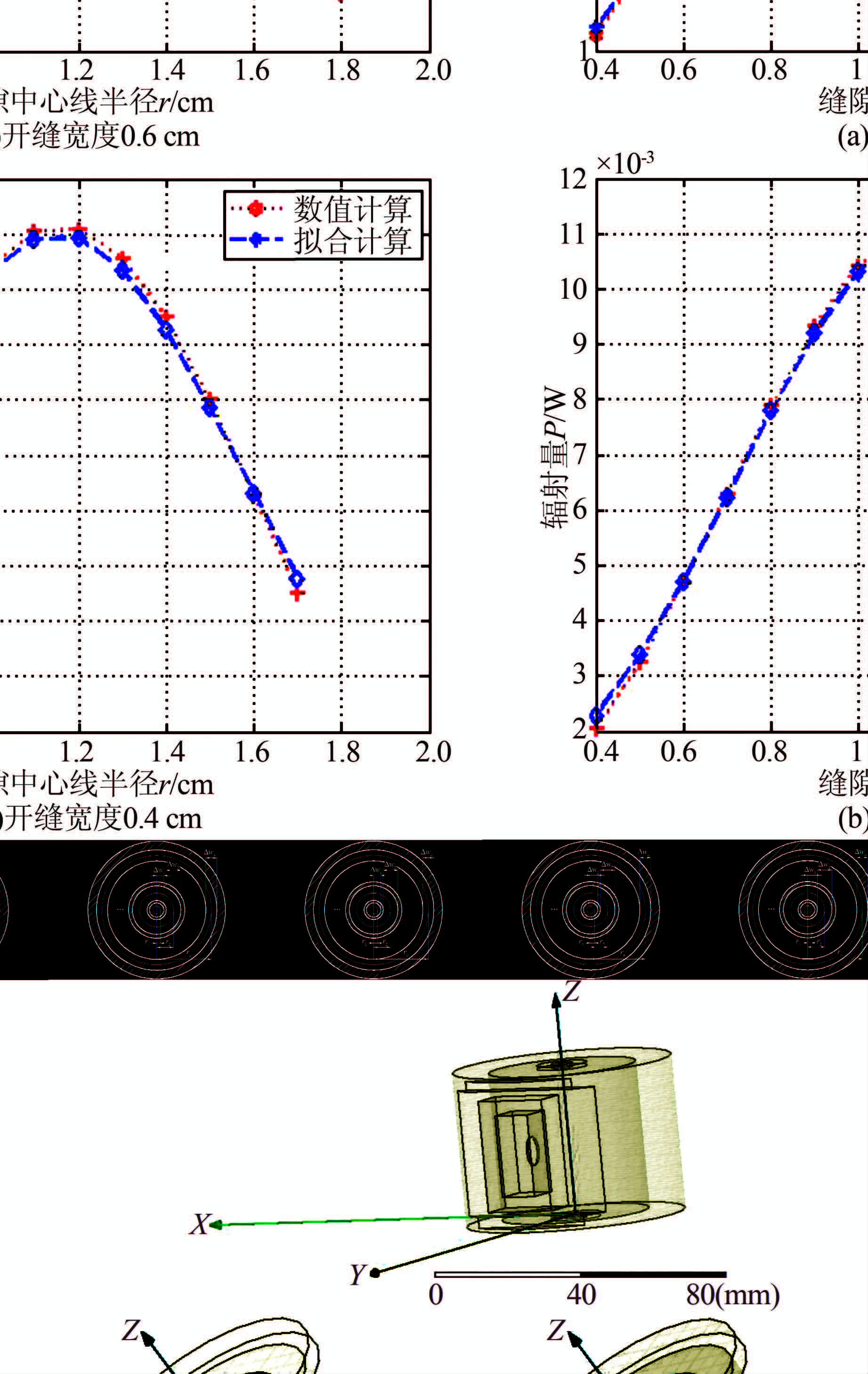
为检验拟合式(3)的准确性，选取开缝宽度Δw分别为0.6、0.4 cm的情况进行检验，结果如图 4、5所示.

图 4 不同开缝宽度时的数值解和式(3)结果比较 Figure 4 The numerical solution of different slit width and type (3) results
图选项
图 5 开缝参量示意图 Figure 5 Schematic diagram of slot parameters
图选项

可知2种情况下的数值计算解和拟合关系式(3)的计算结果十分相近，误差很小.因此拟合关系式(3)可以作为数值计算解的近似计算关系式，用来进行优化计算.

3 缝隙宽度和分布的优化模型 3.1 线性约束优化模型的建立

缝隙宽度和分布的优化目标是找到一种最佳的缝隙分布和每个缝隙的开缝宽度，使得总辐射功率尽可能地小.设开缝个数为n，开缝宽度分别为Δw1，…，Δwn，中圆半径分别为r1，…，rn，可得线性约束优化模型：

$$\eqalign{ & \min \sum\limits_{i = 1}^n {f({r_i},\Delta {w_i})} \cr & s.t. \cr & \left\{ \matrix{ {r_1} - {{\Delta {w_1}} \over 2} = 0 \hfill \cr {\delta _{\min }} \le ({r_{i + 1}} - {{\Delta {w_{i + 1}}} \over 2}) - ({r_i} - {{\Delta {w_i}} \over 2}) \le {\delta _{\max }} \hfill \cr {r_n} - {{\Delta {w_n}} \over 2} = R - {\delta _{outside}} \hfill \cr {r_1} \ge 2mm,{r_j} \ge 1.5\Delta {w_j},j = 2,...,n \hfill \cr} \right. \cr} $$

式中：f(ri,Δwi)为式(3)代表的辐射功率关于开缝宽度和开缝位置的二元关系式；δmin和δmax分别为要求的缝隙之间金属环的最小宽度和最大宽度；δoutside为最外层腔体壁厚;R为谐振腔体的总半径.

优化模型中，第1和第3约束条件分别限定了最内层和最外层缝隙的边界条件；第2约束条件限定了中间各缝隙的边界条件，使每个缝隙不发生重叠；第4约束条件保证了缝隙的蒸汽流通，防止对测量结果的影响.

3.2 优化模型的求解及数值仿真验证

利用上述优化模型，对某一开3个缝隙，谐振腔体总半径R为2 cm的腔体进行优化计算.其中δmin=1 mm，δmax=3 mm.

3个缝隙的开缝位置(中圆半径)、开缝宽度和缝隙外侧的金属环宽度求解结果见表 1.

表 1 缝隙优化求解结果 Table 1 Slot optimization results
mm
缝隙编号
12 3
中圆半径r1.417.665 15.055
开缝宽度Δw2.825.33 4.11
金属环宽度2.182.67 2.89
表选项

求得总辐射功率$\sum\limits_{i=1}^{n}{f({{r}_{i}},\Delta {{w}_{i}})}$为0.011 7 W.为验证优化开缝计算得到的辐射功率的准确性，采用HFSS电磁数值计算软件进行仿真.

首先根据优化得到的尺寸，画出圆柱腔体的三维模型，如图 6所示.

图 6 三维优化圆柱腔体模型 Figure 6 3D model of optimization cylindrical cavity
图选项

然后设定好材料、边界、激励频率等条件，进行数值求解.经过计算得到了腔体的电场强度、磁场强度分布(图 7)以及辐射量等参数.利用HFSS计算，得到的缝隙辐射量为0.012 2 W，与上文的计算值0.011 7 W相近,该优化模型能够用于圆柱谐振腔体的缝隙设计中.

图 7 圆柱腔体的电场强度和磁场强度分布 Figure 7 The electric field intensity and magnetic field intensity distribution of the cylindrical cavity
图选项
4 结论

1) 利用电磁学理论解释了谐振腔测量蒸汽湿度的原理，分析了辐射功率对腔体工作的影响.

2) 利用HFSS计算了腔体辐射功率的数值解，用高斯函数对HFSS仿真数据进行拟合，得到了开缝宽度和开缝位置的二元函数拟合关系式.

3) 建立并求解以辐射功率最小为目标函数的线性约束优化模型，并利用HFSS电磁数值计算软件进行了仿真，验证了方法的可行性.

参考文献
[1] 钱江波, 韩中合. 谐振腔微扰技术测量湿蒸汽两相流的理论分析[J]. 中国电机工程学报, 2012, 32(26): 79–85.
Qian Jiangbo, Han Zhonghe. Theoretical analysis of cavity perturbation techniques for measuring wet steam two-phase Flow[J]. Proceedings of the CSEE, 2012, 32(26): 79–85.
[2] 钱江波. 谐振腔介质微扰技术测量蒸汽湿度的理论与实验研究[D].保定:华北电力大学,2012.
Qian Jiangbo. Theorectical and experimental research on resonant cavity dielectric perturbation technique to measure steam humidity[D]. Baoding: North China Electric Power University, 2012.
[3] 韩中合,汽轮机排汽湿度微波谐振腔测量技术的研究[D].保定:华北电力大学,2006.
Han Zhonghe. Study on the method for measuring flowing steam wetness with microwave resonant cavity perturbation[D]. Baoding: North China Electric Power University, 2006.
[4] 钱江波, 韩中合, 张美凤, 等. 蒸汽参数突变对蒸汽湿度测量的影响分析[J]. 工程热物理学报, 2013, 34(5): 888–891.
Qian Jiangbo, Han Zhonghe, Zhang Meifeng, et al. Analysis of steam parameters mutations affecting to measure steam wetness[J]. Journal of Engineering Thermophysics, 2013, 34(5): 888–891.
[5] 李恒凡. 微波谐振腔测量蒸汽湿度关键问题研究[D].保定:华北电力大学,2014.
Li Hengfan. Research on the key problems of steam humidity measurement in the microwave cavity[D].Baoding: North China Electric Power University, 2014.
[6] 张美凤. 谐振腔微扰法测量蒸汽湿度的误差分析[D].保定:华北电力大学,2013.
Zhang Meifeng. The errors analysis on steam humidity measurement for the method of microwave cavity perturbation[D].Baoding: North China Electric Power University, 2013.
[7] 韩中合, 李恒凡, 严晓哲, 等. 谐振腔水膜和积盐厚度对蒸汽湿度测量的影响[J]. 热力发电, 2014, 43(7): 119–123.
Han Zhonghe, Li Hengfan, Yan Xiaozhe, et al. Influence of water film and salt deposit thickness on cavity's inner surface on steam wetness measurement[J]. Thermal Power Generation, 2014, 43(7): 119–123.
[8] 钱江波, 严晓哲, 韩中合, 等. 微波谐振腔蒸汽湿度测量系统不确定度分析[J]. 动力工程学报, 2014, 34(9): 701–707.
Qian Jiangbo, Yan Xiaozhe, Han Zhonghe, et al. Uncertainly analysis of wetness measurement system by microwave resonant cavity[J]. Journal of Chinese Society of Power Engineering, 2014, 34(9): 701–707.
[9] 刘亚川. 用于蒸汽湿度测量的X波段微波谐振腔设计与制作[D].保定:华北电力大学(河北),2005.
Liu Yachuan. Design and facture of X-Band resonant for wetness measurement in steam[D]. Baoding: North China Electric Power University(He Bei), 2005.
[10] 钱江波, 严晓哲, 韩中合, 等. 流固耦合传热对蒸汽湿度测量传感器的影响[J]. 动力工程学报, 2015, 35(2): 134–140.
Qian Jiangbo, Yan Xiaozhe, Han Zhonghe, et al. Influence of coupled fluid-solid heat transfer on the sensor of steam wetness measurement[J]. Journal of Chinese Society of Power Engineering, 2015, 35(2): 134–140.
[11] 钱江波, 严晓哲, 韩中合. 用于液膜厚度测量的开式同轴腔传感器结构设计[J]. 热力发电, 2015, 44(3): 99–103.
Qian Jiangbo, Yan Xiaozhe, Han Zhonghe. Structural design of microwave coaxial resonant cavity sensor for liquid film thickness measurement[J]. Thermal Power Generation, 2015, 44(3): 99–103.
[12] 钱江波, 韩中合, 严晓哲. 微波同轴腔介质厚度测量理论分析[J]. 工程热物理学报, 2015, 36(8): 1732–1736.
Qian Jiangbo, Han Zhonghe, Yan Xiaozhe. Theoretical analysis of medium thickness measurement by microwave coaxial resonant cavity[J]. Journal of Engineering Thermophysics, 2015, 36(8): 1732–1736.
[13] Han Zhonghe, Qian Jiangbo. Study on a method of steam wetness measurement based on microwave resonant cavity [C]// The Ninth International Conference on Electronic Measurement & Instrument, 2009: 1604-1607.
[14] 钱江波, 韩中合, 张美凤. 汽轮机内湿蒸汽两相流介电性质研究[J]. 中国电机工程学报, 2011, 31(32): 100–106.
Qian Jiangbo, Han Zhonghe, Zhang Meifeng. Study on dielectric properties of wet steam in turbine[J]. Proceedings of the CSEE, 2011, 31(32): 100–106.
[15] 钱江波, 严晓哲, 韩中合, 等. 微波同轴谐振腔测量液膜厚度的理论分析[J]. 汽轮机技术, 2015, 57(2): 89–92.
Qian Jiangbo, Yan Xiaozhe, Han Zhonghe, et al. Theoretical analysis of microwave coaxial resonant cavity technique measuring thickness of liquid film[J]. Turbine Technology, 2015, 57(2): 89–92.